使用对比学习来学习小样本嵌入模型
引用：Liu, Chen, et al. “Learning a few-shot embedding model with contrastive learning.” Proceedings of the AAAI conference on artificial intelligence. Vol. 35. No. 10. 2021.
论文地址：下载地址
论文代码：https://github.com/corwinliu9669/Learning-a-Few-shot-Embedding-Model-with-Contrastive-Learning

Abstract

  小样本学习（FSL）旨在通过适应从源类中学习到的先验知识来识别目标类。这些知识通常存在于深度嵌入模型中，用于支持图像和查询图像对的一般匹配目的。本文的目标是将对比学习重新用于这种匹配，以训练少样本嵌入模型。我们做出了以下贡献：（i）我们在监督环境下研究了带有噪声对比估计（NCE）的对比学习，用于训练少样本嵌入模型；（ii）我们提出了一种新颖的对比训练方案，称为 infoPatch，利用了 patch 级别的关系，显著改进了流行的 infoNCE；（iii）我们证明了由所提出的 infoPatch 学到的嵌入更加有效；（iv）我们的模型在少样本识别任务中进行了全面评估，并在 miniImageNet 上展示了最先进的结果，在 tieredImageNet 和 Fewshot-CIFAR100（FC-100）上取得了令人满意的性能。

1 Introduction

  人类天生具有少样本识别的能力，即通过一个或几个例子进行学习。例如，一个孩子仅凭在电视上看一眼就能轻松识别出“犀牛”。然而，目前大多数成功的基于深度学习的视觉识别系统 ^{1 2 3} 仍然高度依赖于大量的带标签训练数据以及多次迭代来训练其大量参数。最重要的是，这些系统难以将所学知识适应于目标类别。这极大地限制了它们在现实世界中对长尾类别进行开放式学习的可扩展性。

  受到人类小样本学习能力的启发，近年来对单样本/小样本学习的兴趣重新兴起 ^{4 5 6 7 8}。其目标是通过适应从源类中学习到的先验“知识”来识别目标类别。这些知识通常存在于深度嵌入模型中，以用于支持和查询图像对的通用匹配。嵌入模型通常使用源类上足够多的训练实例进行学习，并通过目标类上的少量训练实例进行更新。为了进一步解决目标类数据稀缺的问题，元学习被用来更好地学习深度嵌入模型，从而提高其泛化能力。特别地，FSL 中的元学习范式利用了 episode 的概念 ⁵。每个 episode 应模仿单样本学习任务：从几个类别中抽取少量训练和测试实例来训练/测试嵌入模型；将抽取的训练集输入学习器以产生分类器，然后在抽取的测试集上计算分类器的损失。解决 FSL 的有前景的方法是通过深度卷积网络，然后是线性分类器，学习将查询与少样本支持示例进行匹配。通常，这类方法使用元学习器来训练网络，或者学习与固定度量相一致的深度嵌入空间（如 MatchingNet ⁹ 和 ProtoNet ⁵），或者隐式学习度量并使用二元分类器对新类别数据进行分类（如 RelationNet ⁶）。

  尽管之前做出了很多努力，但小样本学习系统的关键挑战仍在于消除源类的归纳偏差，从而根据新目标类的少量训练实例来调整对假设的偏好。这样的少样本 AI 系统必须处理所学到的少样本嵌入模型在目标类上的泛化能力不足的问题。另一方面，最近的研究 ¹⁰ 表明，改进 FSL 的核心也在于改进所学习的嵌入。特别重要的是，嵌入应将不同类别的实例映射到不同的簇中。此外，从原则上讲，嵌入不应通过记忆训练数据来学习源类的归纳偏差，因为这可能会削弱嵌入的泛化性能。

  为此，本文提出了几项新工作，以解决 FSL 面临的这些挑战。具体来说，我们重新利用对比学习来提升小样本学习的性能。作为一个流行且不断发展的研究课题，对比学习已经在多个与 AI 相关的研究领域中得到了广泛研究和应用。例如，如果对无标签数据进行嵌入模型的预训练，可以在许多下游任务上取得非常出色的性能 ^{11 12}。在这些方法中，infoNCE ¹³ 被广泛使用。值得注意的是，对比学习的关键挑战在于选择具有信息量的正样本对和负样本对 ¹⁴。

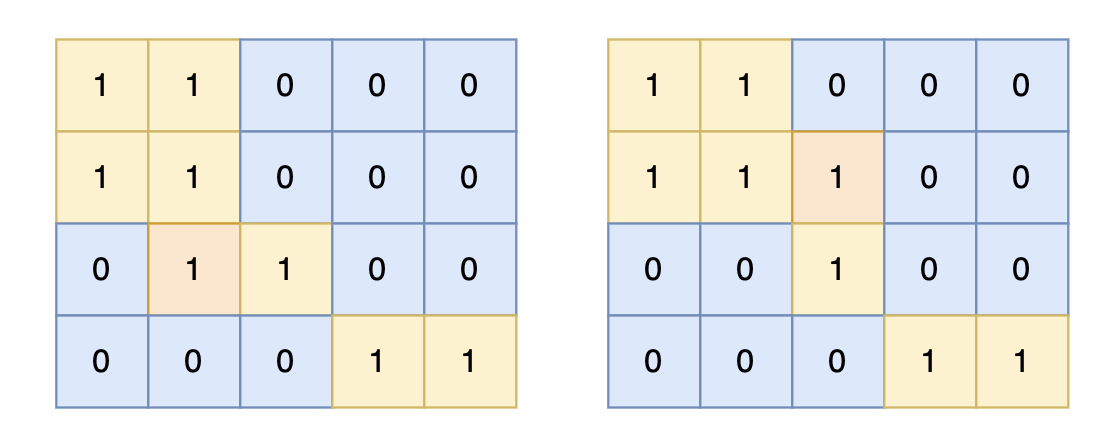
  在本文中，对比学习被扩展并用于小样本学习任务。具体来说，我们提出了通过源类信息构造正样本对和负样本对的算法。在一个 episode 中，我们有支持实例和查询实例。对于每个查询实例，我们可以使用所有支持实例构造正样本和负样本。为了在训练中找到更多有信息量的样本对以获得良好的嵌入，我们提出了生成困难样本的策略。直观地说，作为人类，我们能够仅依赖图像的一部分来识别对象，即使图像的其他部分不可见。这种直觉被用于帮助构建我们的 FSL 对比学习算法。通常情况下，支持图像应该包含足够的信息用于匹配；因此，我们采用随机遮挡图像部分的策略。相应地，查询图像被分割成若干 patch。每个 patch 在图1中进行了说明，这些 patch 被用来帮助少样本识别。因此，即使只给出了图像的一部分，模型也可以学习到对应关系。

图 1: 我们的方法 infoPatch 在此图中进行了说明。左侧部分是我们方法的框架，我们尝试使用困难样本进行对比学习。patch 的定义由网格展示。右侧部分展示了我们 PatchMix 的过程。

  我们进一步做出了另一个贡献，即消除源类数据中的归纳偏差。关键的是，源类的归纳偏差可能不可避免地引入实例与类别之间的意外信息或关联。例如，如果马的图像与草高度相关，则在这种数据上训练的模型可能倾向于将视觉上类似于马的目标图像与草相关联。我们通过将来自不同图像的 patch 混合来缓解这个问题，从而促进嵌入学习更解耦的信息。

  本文的贡献如下：（i）我们以监督方式研究了带有噪声对比估计（NCE）的对比学习，用于训练少样本嵌入模型；（ii）我们提出了一种新的对比训练方案，称为 infoPatch，利用 patch 级关系显著改进了流行的 infoNCE；（iii）我们证明了所提出的 infoPatch 学到的嵌入更加有效；（iv）大量实验表明，我们的简单方法在三个广泛使用的少样本识别基准（包括 miniImageNet、tieredImageNet 和 Fewshot-CIFAR100）上取得了具有竞争力的结果。

2 Related Work

2.1 Few-shot Learning

  少样本学习旨在通过少量标记样本来识别目标类别中的实例。它需要高效的少样本算法以满足许多实际应用，例如分类 ^{15 16 17}，分割 ^{18 19}，生成 ²⁰ 和定位 ²¹。之前的工作大致可以分为两类：优化方法和度量学习方法。

  优化方法包括 MAML ⁴、Reptile ²²、LEO ⁷，以及基于度量学习的方法，例如 ProtoNet ⁵、RelationNet ⁶、TADAM ²³ 和 MatchingNet ⁹。

  基于度量学习的方法试图学习一个良好的嵌入和一个适当的比较度量。CAN ²⁴ 发现支持和查询图像之间的注意力通常未对齐，因此使用了一个交叉注意力模块来缓解该问题。考虑到输入的多样性，Cross Domain ⁸ 通过输入相关的仿射变换层对特征进行转换。FEAT ²⁵ 将少样本学习与 transformer 自注意力机制相结合，并取得了良好性能。²⁶ 提出通过使用三元组损失，可以提高度量学习方法的性能。[ ^12] 通过添加额外的自监督任务来提高泛化性能。DeepEMD ²⁷ 尝试引入一种新的度量来解决该问题。

2.2 Contrastive Learning

  如今，对比学习广泛用于无监督学习。DeepInfomax 从互信息的角度形式化了这个问题。MoCo ¹¹ 使用了内存库和一些实现技巧以获得良好的性能。SimClr ¹² 通过使用更大的批量大小和数据增强改进了对比学习。CMC ²⁸ 尝试将来自不同视角的信息进行组合。目前 ¹⁴ 认为在有监督分类中，infoNCE 相较于交叉熵具有更好的性能。对比学习也被引入到其他领域，例如图像翻译 ²⁹。在 ²⁹ 中，作者提出了在目标图像和源图像的 patch 之间进行对比学习。受此启发，我们在少样本学习场景中定制了一种具有显著区别性实现的新型对比学习方法。

2.3 Data Augmentation

  数据增强是深度学习中的一个重要领域。通过适当的数据增强 ^{30 31 32}，可以显著提高深度网络的性能。例如，mixup ³⁰ 可以提高多个广泛使用的数据集上的分类性能。继 mixup ³⁰ 之后，manifold mixup ³³ 尝试混合特征而不是输入图像。Cutout ³⁴ 在训练期间移除输入图像的一部分。Cutmix ³¹ 通过交换具有随机大小的 patch 并使用类似于 mixup 的混合标签来改进它们。Augmix ³² 结合了几个以随机权重采样的增强输入图像。通过扩展 Cutmix ³¹，我们提出了 PatchMix 增强，这是一种定制算法，可以更好地去除归纳偏差并改进 FSL。在 ³⁵ 中，作者提供了对 mixup ³⁰ 的几种变体的分析。

2.4 FSL and Data Augmentation

  最近的一些 FSL 工作强调了数据增强。Image Hallucination ³⁶ 使用生成器来合成幻觉图像以扩大支持集。IDeMeNet ³⁷ 从图库图像池中采样，从池中选择最相似的图像进行数据增强。在 ³⁸ 中研究了几种常规的数据增强方法。[ ^25] 添加了 manifold mixup ³³ 以增强模型嵌入。

3 Method

3.1 Problem Definition

  在本节中，我们介绍了少样本识别的问题。$X_{\text{train}}$, $X_{\text{val}}$ 和 $X_{\text{test}}$ 分别表示训练集、验证集和测试集。标签集分别记为 $Y_{\text{train}}$, $Y_{\text{val}}$ 和 $Y_{\text{test}}$。整个训练集、验证集和测试集定义为 D train = { X train , Y train } D_{\text{train}} = \{X_{\text{train}}, Y_{\text{train}}\} Dtrain​={Xtrain​,Ytrain​}, D val = { X val , Y val } D_{\text{val}} = \{X_{\text{val}}, Y_{\text{val}}\} Dval​={Xval​,Yval​} 和 D test = { X test , Y test } D_{\text{test}} = \{X_{\text{test}}, Y_{\text{test}}\} Dtest​={Xtest​,Ytest​}。我们将训练集、验证集和测试集的类别记为 $C_{\text{train}}$, $C_{\text{val}}$ 和 $C_{\text{test}}$。

  对于少样本学习（FSL），与常规的监督学习略有不同。训练集和测试集的类别完全不同，即 $C_{\text{train}}\cap C_{\text{test}}=\varnothing$。FSL 的目标是识别新类别的样本。通常情况下，我们需要来自新类别的一些带标签样本，这些样本被称为支持集（support set）。待分类的样本被定义为查询集（query set）。来自支持集的图像被称为支持图像（support images），类似地，查询集中的图像称为查询图像（query images）。一种标准的方式来形式化这种设置是使用“way”和“shot”。“way”表示一次测试过程中新类别的数量，“shot”表示每个类别的支持图像数量；这里我们假设每个类别的支持图像数量相同。因此，我们通常将 FSL 的设置称为 $N$-way, $k$-shot。我们专注于两种主流设置：5-way, 1-shot 和 5-way, 5-shot。另外，我们将每个类别的查询图像数量记为 $n_q$。

3.1.1 Naïve Baseline

最近，一些工作致力于使用有监督的预训练来重建基线 ^{39 40}。正如这些工作中所设想的那样，有监督的预训练可以实现非常有竞争力的 FSL 性能。特别地，这些方法通常在源类上使用交叉熵损失训练网络的分类层。该网络作为目标类的特征提取器；最近邻分类器用于对目标类的样本进行分类。由于其简单性，我们将其作为简单基线。

3.1.2 Overview of InfoPatch

为了通过更具代表性的嵌入来改进简单基线，我们提出了一种名为 infoPatch 的新模型，包括两个组件。其一是一种对比学习方案，它将 infoNCE 损失修改为少样本的方式，并利用增强方法来挖掘困难样本。其二是一种数据增强技术，称为 PatchMix，旨在缓解少样本学习训练过程中的归纳偏差。

3.2 Episodic Contrastive Learning

  在详细介绍我们的模型之前，我们澄清一些符号和定义。在少样本学习（FSL）中，我们将 episode 定义为由 $N\times k$ 支持数据和 $N\times n_q$ 查询数据组成的数据样本。查询实例和支持实例分别记为 $x_q$ 和 $x_s$。它们的标签分别记为 $y_q$ 和 $y_s$。

  我们用 $\Phi$ 表示嵌入网络，例如 ResNet12 ²³。为了方便起见，我们将嵌入网络的输入和输出的张量形状定义为 $C_{\text{in}}\times H_{\text{in}}\times W_{\text{in}}$ 和 $C_{\text{out}}\times H_{\text{out}}\times W_{\text{out}}$。训练和测试过程都采用 $N$-way, $k$-shot 设置来说明。嵌入网络 $\Phi$ 的输出特征表示为 $f$。$f_q$ 和 $f_s$ 分别代表查询和支持的输出特征。为了对比学习，需要对特征进行归一化以便更好地比较。在我们的论文中，$f_q$ 和 $f_s$ 默认被归一化。我们遵循 ¹¹ 对输出特征进行归一化。

3.2.1 训练阶段

  遵循对比学习的思想，我们为每个查询实例构建对比对。这种构建方式与测试阶段相一致。对比对是使用支持特征构建的。对于每个查询实例，我们都有其标签。因此，对于每个查询实例 $x_q^i$，我们将具有相同标签的支持实例视为其正样本对。负样本对则是那些标签不同的样本。对于查询和支持实例，我们使用相同的嵌入网络 $\Phi$。

  一个查询实例 $x_q^i$ 的 infoNCE 可以写成：
$$L_i=-\log \frac{{\sum }_{y_s^j=y_q^i}{f}_q^i{f}_s^j}{{\sum }_{y_s^j=y_q^i}{f}_q^i{f}_s^j+{\sum }_{y_s^k\ne y_q^i}{f}_q^i{f}_s^k}$$
其中 $f_q^i{f}_s^j$ 表示两个特征向量的内积。对于一个 episode 的训练，整个损失是所有查询样本的平均值，表示为 $L=\frac{1}{N\times n_q}{\sum }_{i=1}^{N\times n_q}{L}_i$。在我们的工作中，我们在训练过程中将简单基线中的监督损失和 infoNCE 结合在一起。我们将监督损失和 infoNCE 损失的权重分别设为 1 和 0.5。

3.2.2 测试阶段

  在测试中，我们有带标签的支持样本和无标签的查询样本。目标是预测查询样本。对于每个查询样本，我们计算与所有支持样本的特征内积。此时网络 $\Phi$ 被冻结。具体而言，对于每个查询样本 $x_q^i$，我们首先得到其特征 $f_q^i$。然后我们找到与 $f_q^i$ 内积最大的支持实例：
$$j^{\ast }=\arg \underset{j}{\max }{f}_q^i{f}_s^j$$
然后我们将预测结果赋予 ${\hat{y}}_q^i=y_s^{j^{\ast }}$。

3.3 Construct Hard Samples

  正如 CMC ²⁸ 所示，对比学习的一个关键点在于找到困难样本。找到困难样本的好方法可以迫使模型学习到更多有用的信息。对于识别一个实例，人类并不总是需要看到整个图像。在大多数情况下，图像的一部分就足够了。对于神经网络来说情况也类似。我们认为，使用图像的一部分也可以增强泛化能力。同时，仅提供部分信息可以使模型学习到更多有用的信息。因此，我们认为这可以是一种构建困难样本的好方法。

  基于这个想法，我们建议在训练阶段应修改输入。在 episode 训练过程中，支持图像和查询图像扮演不同的角色。因此，我们为它们选择了不同的修改方法。

  对于支持图像，它们被视为匹配模板，因此我们尽量保持它们完整。为了丢弃部分信息，我们对支持图像应用随机遮罩。这一过程在图1中有说明。通过这种修改，支持图像比原始图像更难识别。我们将这种修改称为随机块（random block）。

  对于查询图像，我们希望将其与支持图像进行匹配，希望即使只有部分查询图像，我们也能得到正确的匹配。我们可以使用网格将输入查询实例分割成若干 patch。patch 的定义是网格中的一个单元，如图1所示。为方便起见，我们假设有 $W\times H$ 个 patch。我们将它们输入嵌入网络，最终得到 $W\times H$ 个特征。对于查询样本 $x_q^i$，我们用向量 $f_{q,i}^{wh}$ 表示。它们每一个都包含了该查询样本的一部分信息。为了充分学习像素之间的关联，我们仍然将整幅图像输入嵌入网络。这样，我们可以得到一个查询实例不同 patch 的 $W\times H$ 输出特征。

损失函数应该稍作修改，形式如下：
$$L_{iwh}=-\log \frac{{\sum }_{y_s^j=y_q^i}{f}_{q,i}^{wh}{f}_s^j}{{\sum }_{y_s^j=y_q^i}{f}_{q,i}^{wh}{f}_s^j+{\sum }_{y_s^k\ne y_q^i}{f}_{q,i}^{wh}{f}_s^k}$$
整个损失函数为：
$$L=\sum _{i=1}^{N\times n_q}\sum _{w=1}^W\sum _{h=1}^H{L}_{iwh}$$
这种改动只用于训练阶段，测试阶段保持不变。

3.4 Enhancing Contrastive Learning via PatchMix

  对于少样本学习（FSL），我们要求在目标类别上实现泛化。在训练阶段，源类别的数据偏差可能会损害泛化能力。数据偏差可能是由于学习到像素之间的不正确关联所导致的。例如，一些特定类别的背景在颜色或纹理上可能相似，嵌入网络可能仅仅记住了这种属性。为了缓解这个问题，我们建议可以混合一些 patch。例如，在混合 patch 后，图像具有更大的多样性，一些简单的关联不再起作用。这样，网络就可以学习到一些真实的规则。

  在实现上，我们随机混合图像的 patch。遵循 Cutmix ³¹，我们使用类似的规则。PatchMix 操作在一个 episode 内部执行。为了避免引入过多噪声，我们只对查询样本进行 PatchMix。具体来说，对于每个查询实例 $x_q^i$，我们从该 episode 中的样本中采样一个不同的实例 $x_q^k$。然后我们随机选择一个框 $(w_1,h_1,w_2,h_2)$。其中，$(w_1,h_1)$ 表示左上角点，$(w_2,h_2)$ 表示右下角点。随机框的采样方式与 Cutmix ³¹ 类似。我们简单地将 $x_q^i$ 的 patch 替换为 $x_q^k$ 的 patch，如下所示：
$$x_q^i[w_1:w_2,h_1:h_2]=x_q^k[w_1:w_2,h_1:h_2]$$

  PatchMix 和 Cutmix 的区别在于混合后的标签。对于 Cutmix，它使用混合标签来训练交叉熵损失。如前所述，我们使用 patch 进行对比学习，因此我们为每个 patch 分配确定性标签。注意，我们混合 patch 只是为了避免简单关联，每个 patch 保留其原始标签。PatchMix 后的实例将被输入到嵌入网络中。损失函数与上一节相同。

4 Experiments

4.1 Dataset and Setting

  为了验证我们的方法，我们在几个广泛使用的数据集上进行了实验。miniImageNet ⁹ 是 ImageNet ⁴¹ 的一个子数据集。它共有 100 个类别，每个类别有 600 个实例。这些类别被划分为训练集、验证集和测试集，分别包含 64、16 和 20 个类别。此划分遵循 ⁴² 的说明。tieredImageNet 也从 ImageNet ⁴¹ 中采样。它由 608 个类别的 779,165 张图像组成。根据 ⁴³ 的建议，它们被分为 351 个用于训练，97 个用于验证，160 个用于测试。Fewshot-CIFAR100（FC100）数据集 ²³ 是 CIFAR-100 的一个子集。常见的划分为 60、20 和 20 个类别用于训练、验证和测试集。

  在训练和测试过程中，tieredImageNet 和 miniImageNet 的图像首先被调整为 84 × 84 的大小。FC100 的图像调整为 32 × 32。在训练过程中，随机水平翻转和随机裁剪被用作常见的数据增强，正如 ²⁴ 中所使用的。

4.1.1 Implementation Details.

  ResNet12 是我们选择的模型结构，细节遵循 TADAM ²³ 中提出的版本。我们使用 he-normal ⁴⁴ 对模型进行初始化。随机梯度下降（Stochastic Gradient Descent, SGD） ⁴⁵ 被选为我们的优化器。初始学习率为 0.1。对于 miniImageNet，我们在第 12,000、14,000 和 16,000 个 episode 时降低学习率。对于 tieredImageNet，每经过 24,000 个 episode，学习率减半。在所有实验中，我们测试模型 2000 个 episode。每次训练期间，从每个 batch 中抽取 4 个 episode。

4.1.2 Metric for Comparison.

  我们在两种设置下进行了实验：5-way 1-shot 和 5-way 5-shot。我们报告平均准确率以及 95% 置信区间，以与其他方法进行比较。对于消融实验和进一步讨论，仅报告平均准确率。

4.2 Comparison with State-of-the-art

4.2.1 Competitors.

  为了验证我们的模型表现，我们选择了几个之前的方法进行比较。例如 ProtoNet ⁵，MAML ⁴，CAN ²⁴，FEAT ⁴⁶，Cross Domain ⁸ 等。这些方法要么是少样本学习（FSL）中的经典方法，要么是具有最佳报告结果的方法。

Model	Backbone	miniImageNet 1-shot	miniImageNet 5-shot	tieredImageNet 1-shot	tieredImageNet 5-shot
ProtoNet 5 MatchingNet 9 RelationNet 18 MAML 4	Conv4	44.42±0.84 48.14±0.78 49.31±0.85 46.47±0.82	64.24±0.72 63.48±0.66 66.60±0.69 62.71±0.71	53.31±0.89 - 54.48±0.93 51.67±1.81	72.69±0.74 - 71.32±0.78 70.30±1.75
LEO 29 PPA 19 wDAE 47 CC+rot 48	WRN-28	61.76±0.08 59.60±0.41 61.07±0.15 62.93±0.45	77.59±0.12 73.74±0.19 76.75±0.11 79.87±0.33	66.33±0.05 - 68.18±0.16 70.53±0.51	81.44±0.09 - 83.09±0.12 84.98±0.36
ProtoNet 38 MatchingNet 38 RelationNet 38 MAML 38 Cross Domain 8	Res-10	51.98±0.84 54.49±0.81 52.19±0.83 51.98±0.84 66.32±0.80	72.64±0.64 68.82±0.65 70.20±0.66 66.62±0.83 81.98±0.55	- - - - -	- - - - -
TapNet 33 MetaOptNet 49 CAN 24 FEAT 46 DeepEMD 21 Negative Margin 20 Rethink-Distill 36 infoPatch	Res-12	61.65±0.15 62.64±0.61 63.85±0.48 66.78±0.20 65.91±0.82 63.85±0.81 64.82±0.60 67.67±0.45	76.36±0.10 78.63±0.46 79.44±0.34 82.05±0.14 82.41±0.56 81.57±0.56 82.14±0.43 82.44±0.31	- 65.99±0.72 69.89±0.51 70.80±0.23 71.16±0.87 - 71.52±0.69 71.51±0.52	- 81.56±0.53 84.23±0.37 84.79±0.16 86.03±0.58 - 86.03±0.49 85.44±0.35

表 1：miniImageNet 和 tieredImageNet 数据集上的 5-way 少样本学习准确率（95% 置信区间）。所有竞争方法的结果均来自其原始论文。

4.2.2 Discussion

  结果如表 1 所示。与其他具有复杂结构或更大网络（WRN28）的方法相比，我们实现了明显的增益，与 FEAT ⁴⁶ 相比，约提高 1%。由于没有为模型添加额外的结构，我们相比于其他方法（例如 CAN ²⁴）有更清晰的推理逻辑。

  FC100 上的结果如表 2 所示，我们的模型在其中取得了有竞争力的性能。

Model	FC100 accuracies 5-way 1-shot	FC100 accuracies 5-way 5-shot
MAML	38.1±1.7	50.4±1.0
MAML++	38.7±0.4	52.9±0.4
T-NAS++	40.4±1.2	54.6±0.9
TADAM	40.1±0.4	56.1±0.4
ProtoNet	37.5±0.6	52.5±0.6
MetaOptNet	41.1±0.6	55.5±0.6
DC	42.0±0.2	57.1±0.2
DeepEMD	46.5±0.8	63.2±0.7
Rethink-Distill	44.6±0.7	60.1±0.6
infoPatch	43.8±0.4	58.0±0.4

表 2：FC100 数据集上的 5-way 少样本学习准确率（95% 置信区间）。所有竞争方法的结果均来自其原始论文。

4.3 Ablation Study

4.3.1 我们方法的分析

  对于我们的方法，我们包含不同的部分：infoNCE、hard sample 和 PatchMix。如表 5 所示，每一部分都对性能提升有所贡献。在这次分析中，我们只使用 miniImageNet。我们发现，每个部分都做出了显著贡献。通过使用 infoNCE，与基线相比，我们可以提升超过 2%。使用我们提出的 hard sample，模型具有更好的泛化能力，在 1-shot 分类中的性能达到 66.8%。对于 PatchMix，我们发现它可以进一步提高模型性能约 1%。

Model	FC100 accuracies 5-way 1-shot	FC100 accuracies 5-way 5-shot
MBaseline	61.69	78.31
+ infoNCE	64.23	79.17
+ hard sample	66.80	81.35
+ PatchMix	67.67	82.44

表 5：我们模型的消融研究，可以发现模型的每个部分都具有重要的贡献。

4.3.2 网格大小的消融实验

  在构建困难样本时，我们需要为 patch 定义网格。为了方便起见，我们只在 miniImageNet 上进行分析实验。我们选择了三种网格大小：$1\times 1$、$6\times 6$ 和 $11\times 11$。对于 $1\times 1$，我们使用整幅图像进行对比学习。如表 4(b) 所示，使用较大的网格大小可以获得更好的结果。我们没有尝试更大的网格，因为输入大小为 $84\times 84$，较大的网格大小可能会在 patch 中引入更多噪声。对于适中的网格大小，我们可以找到困难样本，从而提高性能。

4.3.3 PatchMix 的有效性

  为了验证我们所提出方法的有效性，我们进行了以下两个实验。我们将 PatchMix 插入到其他现有的少样本学习方法中，例如 RelationNet 和 CAN。注意，我们将 RelationNet 的输出修改为一个向量而不是标量，以使其与 patch 级损失兼容。表 3(a) 中的结果与表 5 相似。第一个实验说明了我们的增强方法可以直接应用于其他 FSL 方法并提高其性能。这证明了我们的方法是一种可以广泛用于 FSL 的通用方法。

Model	k 1	k 5
R-Net	52.78	68.11
R-Net + P-mix	53.50	68.67
CAN	63.85	79.44
CAN + P-mix	64.65	79.86

表 3(a) R-Net：RelationNet，P-mix：PatchMix。显示了 PatchMix 与其他方法（RelationNet 和 CAN）的组合。

Type	k 1	k 5
Ind-mix	67.67	82.44
S-mix	67.53	81.94
E-mix	67.48	82.06

表 3(b) Ind-mix：独立混合，S-mix：共享混合，E-mix：交换混合。表 (b) 显示了对不同 PatchMix 实现的消融研究。

  为了进一步验证 PatchMix 的有效性，我们选择了其他几种数据增强方法进行比较。实验在 miniImageNet 上进行，除了详细的数据增强方法外，其他设置相同。我们将 Augmix ³² 和 Cutmix ³¹ 添加到我们的基线方法中。同时，我们使用了 manifold mixup ⁵⁰ 和 IDeMeNet ³⁸ 中的增强方法。表 4(a) 中报告了结果。显然，我们的 PatchMix 给出了最好的结果。

Augment	k 1	k 5
mixup	66.64	80.99
augmix	66.90	81.27
cutmix	66.34	81.43
IDeMeNet	66.59	81.12
M-mixup	66.92	81.41
PatchMix	67.67	82.44

表 4(a) M-mixup：流形混合。表 (a) 包含与其他增强方法的比较。

grid size	k 1	k 5
1×1	64.23	79.17
6×6	66.19	81.27
11×11	66.80	81.35

表 4(b) 显示了不同网格大小的结果。注意，在此实验中，6×6 和 11×11 的情况下未包含 PatchMix。我们发现，对于我们的设置，选择 11×11 的大小是一个不错的选择。

4.3.4 PatchMix 的实现

  我们通过在样本之间交换 patch 来实现 PatchMix。在本节中，我们还讨论了详细的实现。对于默认实现，我们在每个 episode 内部执行 PatchMix。我们将这种实现称为独立混合（independent mix）。目前，一些工作提出修改采样策略。例如，我们可以采样两个具有相同类别的 episode。这两个 episode 中的图像完全不同。在这种采样策略下，这两个 episode 是相似的。因此，我们尝试了两种变体的实现。第一种被称为共享混合（share mix）。对于共享混合，我们在两个 episode 内部执行 PatchMix。另一种被称为交换混合（exchange mix），它通过使用来自相似 episode 的样本（而不是它们所属的 episode）来执行 PatchMix。通过观察表 3(b) 中的结果，我们可以发现 PatchMix 在混合策略方面具有鲁棒性。

4.4 Visualizations

  我们方法的有效性是显著的。本节通过可视化探索性能提升的机制。

  首先，我们通过 tSNE 图来可视化嵌入。具体来说，我们从 miniImageNet 的目标类别中采样一个 episode，将其输入基线模型和完整模型。嵌入可视化结果如图 3 所示。从图 3 中可以观察到，我们方法生成的簇比基线方法更加紧凑。

图 3：我们对目标类别的一些样本进行了 tSNE 可视化。左图为基线模型的可视化结果，右图为我们模型的结果。显然，我们的模型能够更好地聚类样本。图中不同颜色代表不同的类别。

  此外，我们通过可视化空间对应关系来验证是否可以通过部分信息来识别图像。同样地，我们从 miniImageNet 的目标类别中采样一个 episode。我们使用支持图像的特征来计算查询图像每个 patch 的内积。热图分数在图 2 中显示。从图 2 中可以看出，我们的方法在空间关系上优于基线方法。我们的模型更准确、完整地覆盖了前景。这也可以被视为更好表征的证据。

图 2：展示了图像及其空间对应关系的热图。我们利用网络生成的支持样本特征与查询图像特征计算内积，并将内积以热图的形式可视化。可以发现，我们的模型能够更精确地定位目标对象。本部分使用来自目标类别的图像进行展示。

5 Conclusion

  在本文中，我们展示了如何以监督的方式使用带有噪声对比估计（Noise Contrastive Estimation, NCE）的对比学习来训练用于少样本识别的深度嵌入模型。基于这一观察，我们提出了一种新的对比训练方案，称为 infoPatch，它利用 patch 级关系显著改进了流行的 infoNCE。我们证明了所提出的 infoPatch 学到的嵌入更加有效。我们在少样本识别任务中对我们的方法进行了全面评估，并在 miniImageNet 上取得了最先进的结果，同时在 tieredImageNet 和 Fewshot-CIFAR100（FC-100）上也表现出了令人满意的性能。

---

1. Krizhevsky, A.; Sutskever, I.; and Hinton, G. E. 2012. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems 25: 1097–1105. ↩︎

2. He, K.; Zhang, X.; Ren, S.; and Sun, J. 2016. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, 770–778. ↩︎

3. He, K.; Gkioxari, G.; Dollár, P.; and Girshick, R. 2017. Mask r-cnn. In Proceedings of the IEEE international conference on computer vision, 2961–2969. ↩︎

4. Finn, C.; Abbeel, P.; and Levine, S. 2017. Model-agnostic meta-learning for fast adaptation of deep networks. In International Conference on Machine Learning, 1126–1135. PMLR. ↩︎ ↩︎ ↩︎ ↩︎

5. Snell, J.; Swersky, K.; and Zemel, R. S. 2017. Prototypical networks for few-shot learning. arXiv preprint arXiv:1703.05175. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

6. Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P. H.; and Hospedales, T. M. 2018. Learning to compare: Relation network for few-shot learning. In Proceedings of the IEEE conference on computer vision and pattern recognition, 1199–1208. ↩︎ ↩︎ ↩︎

7. Rusu, A. A.; Rao, D.; Sygnowski, J.; Vinyals, O.; Pascanu, R.; Osindero, S.; and Hadsell, R. 2018. Meta-learning with latent embedding optimization. arXiv preprint arXiv:1807.05960. ↩︎ ↩︎

8. Tseng, H.-Y.; Lee, H.-Y.; Huang, J.-B.; and Yang, M.-H. 2020. Cross-domain few-shot classification via learned feature-wise transformation. arXiv preprint arXiv:2001.08735. ↩︎ ↩︎ ↩︎ ↩︎

9. Vinyals, O.; Blundell, C.; Lillicrap, T.; Kavukcuoglu, K.; and Wierstra, D. 2016. Matching networks for one shot learning. arXiv preprint arXiv:1606.04080. ↩︎ ↩︎ ↩︎ ↩︎

10. Tian, Y.; Wang, Y.; Krishnan, D.; Tenenbaum, J. B.; and Isola, P. 2020. Rethinking few-shot image classification: a good embedding is all you need? arXiv preprint arXiv:2003.11539. ↩︎

11. Chen, X.; Fan, H.; Girshick, R.; and He, K. 2020b. Improved baselines with momentum contrastive learning. arXiv preprint arXiv:2003.04297. ↩︎ ↩︎ ↩︎

12. Chen, T.; Kornblith, S.; Norouzi, M.; and Hinton, G. 2020a. A simple framework for contrastive learning of visual representations. In International conference on machine learning, 1597–1607. PMLR. ↩︎ ↩︎

13. Oord, A. v. d.; Li, Y.; and Vinyals, O. 2018. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748. ↩︎

14. Khosla, P.; Teterwak, P.; Wang, C.; Sarna, A.; Tian, Y.; Isola, P.; Maschinot, A.; Liu, C.; and Krishnan, D. 2020. Supervised contrastive learning. arXiv preprint arXiv:2004.11362. ↩︎ ↩︎

15. Fei-Fei, L.; Fergus, R.; and Perona, P. 2006. One-shot learning of object categories. IEEE transactions on pattern analysis and machine intelligence 28(4): 594–611. ↩︎

16. Wang, Y.; Zhang, L.; Yao, Y.; and Fu, Y. 2020b. How to trust unlabeled data? Instance Credibility Inference for Few-Shot Learning. arXiv preprint arXiv:2007.08461. ↩︎

17. Wang, Y.; Xu, C.; Liu, C.; Zhang, L.; and Fu, Y. 2020a. Instance credibility inference for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 12836–12845. ↩︎

18. Wang, K.; Liew, J. H.; Zou, Y.; Zhou, D.; and Feng, J. 2019. Panet: Few-shot image semantic segmentation with prototype alignment. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 9197–9206. ↩︎ ↩︎

19. Rakelly, K.; Shelhamer, E.; Darrell, T.; Efros, A. A.; and Levine, S. 2018. Few-shot segmentation propagation with guided networks. arXiv preprint arXiv:1806.07373. ↩︎ ↩︎

20. Liu, M.-Y.; Huang, X.; Mallya, A.; Karras, T.; Aila, T.; Lehtinen, J.; and Kautz, J. 2019. Few-shot unsupervised image-to-image translation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 10551–10560. ↩︎ ↩︎

21. Wertheimer, D.; and Hariharan, B. 2019. Few-shot learning with localization in realistic settings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 6558–6567. ↩︎ ↩︎

22. Nichol, A.; Achiam, J.; and Schulman, J. 2018. On first-order meta-learning algorithms. arXiv preprint arXiv:1803.02999. ↩︎

23. Oreshkin, B. N.; Rodriguez, P.; and Lacoste, A. 2018. TADAM: task dependent adaptive metric for improved few-shot learning. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, 719–729. ↩︎ ↩︎ ↩︎ ↩︎

24. Hou, R.; Chang, H.; Ma, B.; Shan, S.; and Chen, X. 2019. Cross attention network for few-shot classification. arXiv preprint arXiv:1910.07677. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

25. Ye, H.-J.; Hu, H.; Zhan, D.-C.; and Sha, F. 2020. Few-shot learning via embedding adaptation with set-to-set functions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8808–8817. ↩︎

26. Wang, Y.; Wu, X.-M.; Li, Q.; Gu, J.; Xiang, W.; Zhang, L.; and Li, V. O. 2018a. Large margin meta-learning for few-shot classification. In Proc. 2nd Workshop Meta-Learn. NeurIPS, 1–8. ↩︎

27. Zhang, C.; Cai, Y.; Lin, G.; and Shen, C. 2020. DeepEMD: Few-Shot Image Classification With Differentiable Earth Mover’s Distance and Structured Classifiers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 12203–12213. ↩︎

28. Tian, Y.; Krishnan, D.; and Isola, P. 2019. Contrastive multiview coding. arXiv preprint arXiv:1906.05849. ↩︎ ↩︎

29. Park, T.; Efros, A. A.; Zhang, R.; and Zhu, J.-Y. 2020. Contrastive learning for unpaired image-to-image translation. In European Conference on Computer Vision, 319–345. Springer. ↩︎ ↩︎ ↩︎

30. Zhang, H.; Cisse, M.; Dauphin, Y. N.; and Lopez-Paz, D. 2017. mixup: Beyond empirical risk minimization. arXiv preprint arXiv:1710.09412. ↩︎ ↩︎ ↩︎ ↩︎

31. Yun, S.; Han, D.; Oh, S. J.; Chun, S.; Choe, J.; and Yoo, Y. 2019. Cutmix: Regularization strategy to train strong classifiers with localizable features. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 6023–6032. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

32. Hendrycks, D.; Mu, N.; Cubuk, E. D.; Zoph, B.; Gilmer, J.; and Lakshminarayanan, B. 2019. Augmix: A simple data processing method to improve robustness and uncertainty. arXiv preprint arXiv:1912.02781. ↩︎ ↩︎ ↩︎

33. Verma, V.; Lamb, A.; Beckham, C.; Najafi, A.; Mitliagkas, I.; Lopez-Paz, D.; and Bengio, Y. 2019. Manifold mixup: Better representations by interpolating hidden states. In International Conference on Machine Learning, 6438–6447. PMLR. ↩︎ ↩︎ ↩︎

34. DeVries, T.; and Taylor, G. W. 2017. Improved regularization of convolutional neural networks with cutout. arXiv preprint arXiv:1708.04552. ↩︎

35. Summers, C.; and Dinneen, M. J. 2019. Improved mixed-example data augmentation. In 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), 1262–1270. IEEE. ↩︎

36. Wang, Y.-X.; Girshick, R.; Hebert, M.; and Hariharan, B. 2018b. Low-shot learning from imaginary data. In CVPR. ↩︎ ↩︎

37. Chen, Z.; Fu, Y.; Wang, Y.-X.; Ma, L.; Liu, W.; and Hebert, M. 2019c. Image deformation meta-networks for one-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8680–8689. ↩︎

38. Chen, Z.; Fu, Y.; Chen, K.; and Jiang, Y.-G. 2019b. Image block augmentation for one-shot learning. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, 3379–3386. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

39. Liu, C.; Xu, C.; Wang, Y.; Zhang, L.; and Fu, Y. 2020b. An Embarrassingly Simple Baseline to One-Shot Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, 922–923. ↩︎

40. Dhillon, G. S.; Chaudhari, P.; Ravichandran, A.; and Soatto, S. 2019. A baseline for few-shot image classification. arXiv preprint arXiv:1909.02729. ↩︎

41. Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. 2015. Imagenet large scale visual recognition challenge. International journal of computer vision 115(3): 211–252. ↩︎ ↩︎

42. Ravi, S.; and Larochelle, H. 2017. Optimization as a model for few-shot learning. In In International Conference on Learning Representations (ICLR). ↩︎

43. Ren, M.; Triantafillou, E.; Ravi, S.; Snell, J.; Swersky, K.; Tenenbaum, J. B.; Larochelle, H.; and Zemel, R. S. 2018. Meta-learning for semi-supervised few-shot classification. arXiv preprint arXiv:1803.00676. ↩︎

44. He, K.; Zhang, X.; Ren, S.; and Sun, J. 2015. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE international conference on computer vision, 1026–1034. ↩︎

45. Bottou, L. 2010. Large-scale machine learning with stochastic gradient descent. In Proceedings of COMPSTAT’2010, 177–186. Springer. ↩︎

46. Fei, N.; Lu, Z.; Gao, Y.; Tian, J.; Xiang, T.; and Wen, J.-R. 2020. Meta-learning across meta-tasks for few-shot learning. arXiv preprint arXiv:2002.04274. ↩︎ ↩︎ ↩︎

47. Gidaris, S.; Bursuc, A.; Komodakis, N.; Pérez, P.; and Cord, M. 2019. Boosting few-shot visual learning with self-supervision. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 8059–8068. ↩︎

48. Gidaris, S.; and Komodakis, N. 2019. Generating classification weights with gnn denoising autoencoders for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 21–30. ↩︎

49. Liu, B.; Cao, Y.; Lin, Y.; Li, Q.; Zhang, Z.; Long, M.; and Hu, H. 2020a. Negative margin matters: Understanding margin in few-shot classification. In European Conference on Computer Vision, 438–455. Springer. ↩︎

50. Mangla, P.; Kumari, N.; Sinha, A.; Singh, M.; Krishnamurthy, B.; and Balasubramanian, V. N. 2020. Charting the right manifold: Manifold mixup for few-shot learning. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, 2218–2227. ↩︎