Leader-aware community detection in complex networks
- Leader-aware community detection algorithm - 领导感知社区检测算法
- 创新点
- 相关工作
- 概念定义
- 基础概念
- 创新概念
- 1. (领导力)
- 2. (边缘紧性)
- 3.(引力)
- 模型
- 1. 确定地方领导人
- 2. 构建依赖树
- 3.合并分支
- 算法优点
- 实验
- 指标
- 人工合成网络
- 真实网络
Leader-aware community detection algorithm - 领导感知社区检测算法
Autoleader核心思想: 该算法对每个节点的领导度进行度量,并让每个节点都依附于其本地领导度,形成依赖树。一旦所有的依赖树都确定了,社区结构就出现了,因为其中一棵树实际上是一个集群。
此外,树的每个根节点恰好是相应社区的领导者.该方法可以快速确定每个节点的归属。
创新点
-
计算了从一个节点到另一个节点的引力。
-
每个节点基于领导力和吸引力,依附于邻近的本地领导者,形成有向依赖链接。
在领导的基础上,每个节点以级联的方式指向它的本地领导,自发地形成了原创的社区结构。
在我们的算法扫描了所有节点后,一个包含至少一棵树的森林出现了。
建立依赖树,在形成社区的过程中获得社区领袖。 -
由于聚类过程中可能存在一些细小的分支,因此需要进行合并,以提高聚类质量。
最后,解决所有可用的链接。 -
每棵树代表一个社区,根节点是相应社区的领导者。
从依赖树中,我们可以清楚地认识到一个社区是如何形成的隐藏规则。
相关工作
-
基于模块化的算法是解决社区检测问题的常用算法。并成为使用最多和最著名的质量函数。
模块化优化是一个np完全问题,许多算法的目标都是求图划分的模块化最大值的近似。 -
基于模块化优化模型的深度神经网络非线性重构新方法。
缺点:模块化优化有一个分辨率限制,这可能会阻止它检测到相对于整个图而言相对较小的簇。 -
基于DBSCAN(基于密度的聚类算法)的结构聚类算法SCAN
缺点:SCAN的限制在于需要用户自定义参数,这在一定程度上影响了图聚类的结果。 -
利用随机游走理论进行群落检测,来自位于自己社区内的节点的随机漫步的概率比来自外部的节点的随机漫步的概率高,因为社区内的连接应该更密集。
Infomap - 是一种具有代表性的基于最小描述长度原则寻找最优划分的方法,采用改进的模块化优化策略来挖掘社区。
Walktrap - 是另一种基于随机游走的方法,可以检测分层集群。 -
具体的规则来指导社区的形成,而随机游走方法则利用统计策略。
-
Leader-follower方法Top Leaders假设社区是一组聚集在领导者附近的追随者节点。
它首先在一个特定的网络中识别有前途的领导者;
然后,迭代地将追随者聚集到他们最亲近的领导者那里,形成社区。
缺点:主要的限制是它需要社区的数量k作为一个预定义的参数。
在本研究中,我们对原有的模型进行了改进,提出了一种利用leader-follower链实现鲁棒聚类的新方法。 -
LPA - 是一种利用标签在全网传播的算法。
缺点:该算法可以在近线性时间内检测到社区结构,但由于其更新顺序随机,结果不稳定。 -
基于距离动力学的新方法,取得了良好的性能
-
BlackHole - 灵感来自于图形绘制
-
基于光谱聚类上也有一些强大的方法
缺点:是这类方法对参数敏感,对矩阵依赖程度高,不同的相似矩阵会导致不同的聚类性能。 -
深度学习技术对复杂网络的研究:1)探索了图和图聚类的新表示方法 2)寻求利用深度学习策略检测社区的新方法
缺点:所有这些方法都只是揭露社区,而完全忽略了社区中心的存在。
在本文中,我们提出了一种新的链式社区结构研究算法,它不仅可以检测到社区,而且可以识别每个集群的领导者。
概念定义
我们需要解决的问题是在网络中检测非重叠的社区结构及其领导者。
为方便起见,我们利用无权无向图作为研究对象。
基础概念
-
(结构邻域) 给定一个无向图G = (V, E),节点u∈V,节点u的结构邻域是包含自身及其与节点u有连接的相邻节点的节点集T (u)
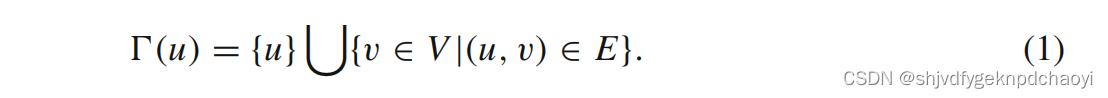
-
(唯一邻居) 对于图G = (v, E)的边(u, v)∈E,节点u的唯一邻居是只与u相连,与节点v没有连接的节点,可表示为:
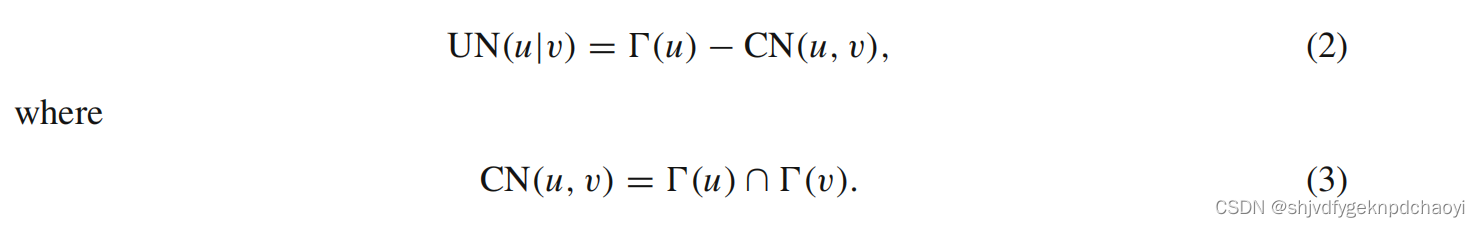
( CN(u, v) is the common neighbors of the two nodes u and v ) -
(Jaccard相似度和Jaccard距离) 给定无向图G = (V, E),节点u和V的Jaccard相似度为
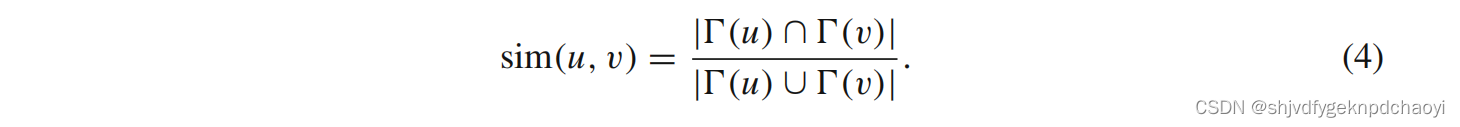 在此基础上,可计算相邻两个节点u和v之间的Jaccard距离:
在此基础上,可计算相邻两个节点u和v之间的Jaccard距离:
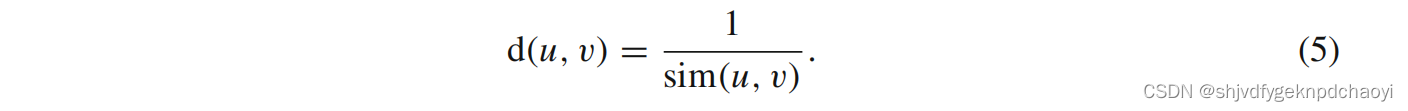
相似度越高,距离越短
创新概念
1. (领导力)
给定无向图G = (V, E)中的节点u∈V,定义节点u的领导力为:
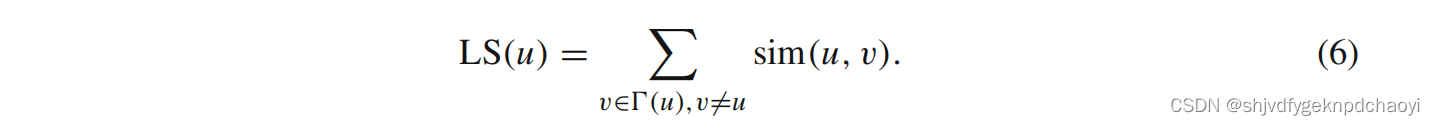
节点的领导级别取决于它的邻居的数量以及它与邻居之间的亲密程度。
每个链接的相似度决定了每对节点的紧密程度。
这在现实场景中也是合理的。
与他人有很多密切关系的人更有可能成为领导者。
与邻居联系密切的节点的影响比那些与邻居联系较少的节点传播得更快,而且影响往往更强大,因为它们的邻居会受到节点本身和其他邻居的影响。
仅仅考虑节点的度并不能反映其领导力。
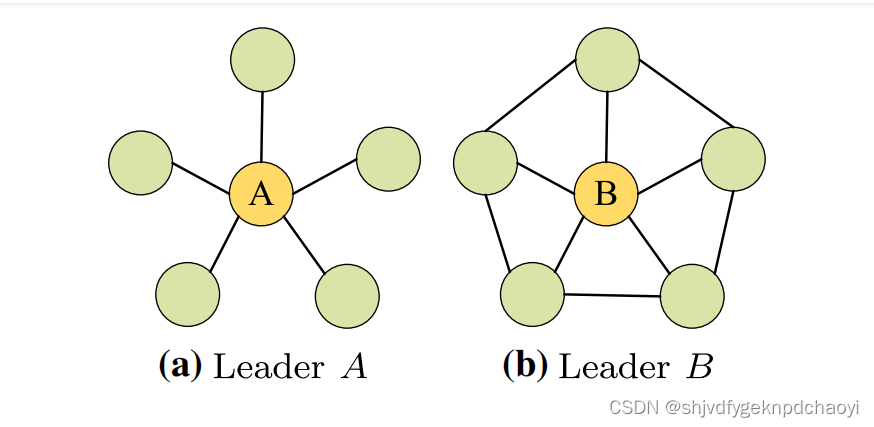
(两个子图,它们的中心节点有相同的度,但不同的领导)
领导力用于从局部角度衡量节点的影响力。
它在很大程度上决定了一个节点是否可以成为相邻节点的本地领导。
对于任何一对连接的节点,如果知道它们的领导,就可以解决leader-follower的关系。
2. (边缘紧性)
图中边(u, v)∈E的边紧度,G = (V, E)表示两个端点之间的距离。有三种模式需要考虑。

第一项很容易理解,度量两个节点的相似性(Jaccard相似度,概念3.)。
第二项强调两个端点的共同邻居的重要性,这加强了它们之间的联系。
第三项更加复杂:
1)如果一个唯一的邻居和另一个端点之间的相似性小于阈值,则会导致与第二种情况相反的效果。
2)否则,与第二种情况相同。
参数λ的取值范围为0 ~ 1,它决定了由这些独特的相邻点引起的相互作用力的方向:接近或远离。我们将在实验部分进一步讨论该参数。
玩具网络的边EC图
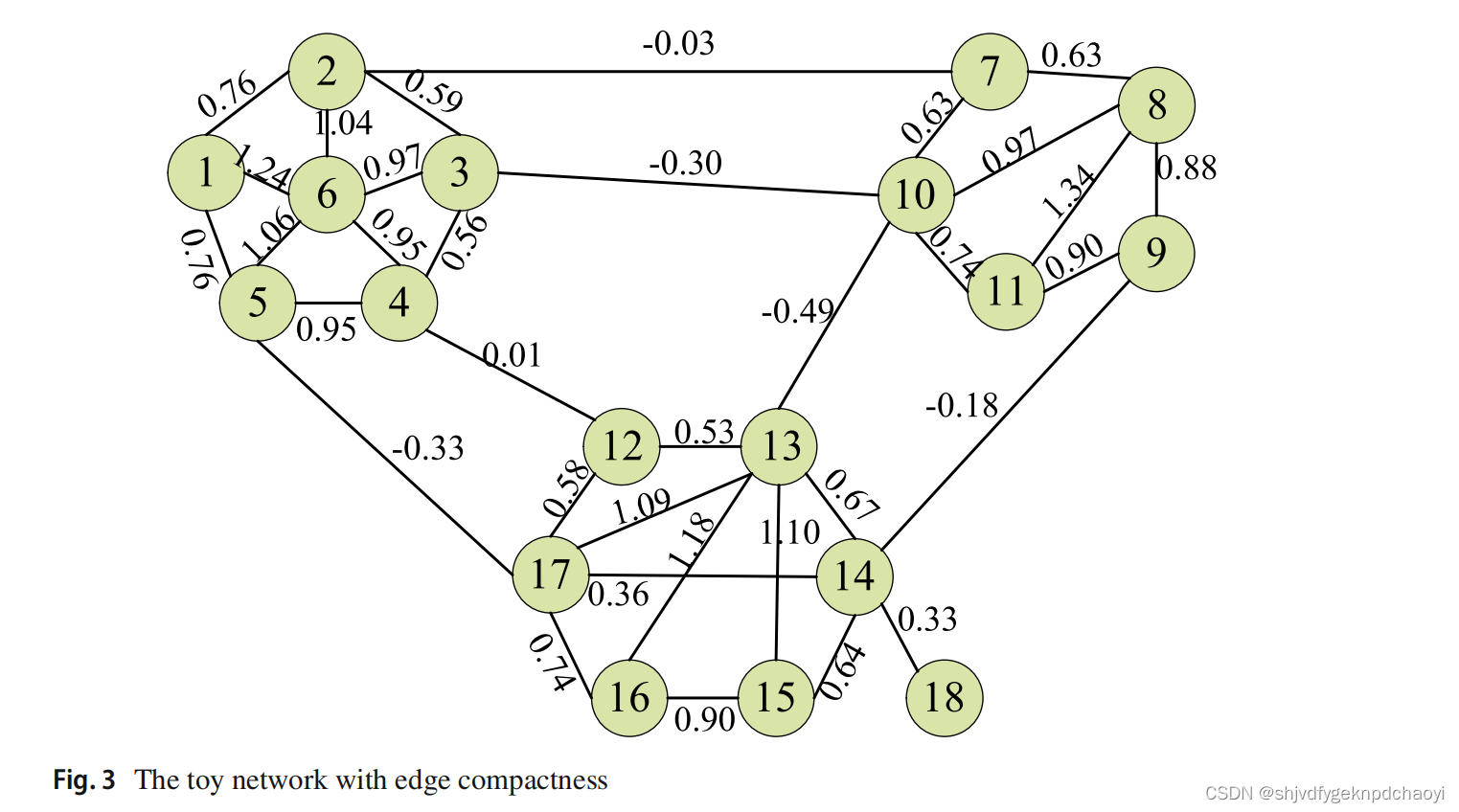
EC的相关结论:
引理3.1 对于边(u, v)∈E,给定λ参数,如果EC(u, v) < 0,则节点u和节点v不在同一团体内。因此合理的潜在的局部领导权节点需要EC值非负。
3.(引力)
图G = (v, E)中,对于节点v及其相邻节点u,节点u对节点v施加的引力为:
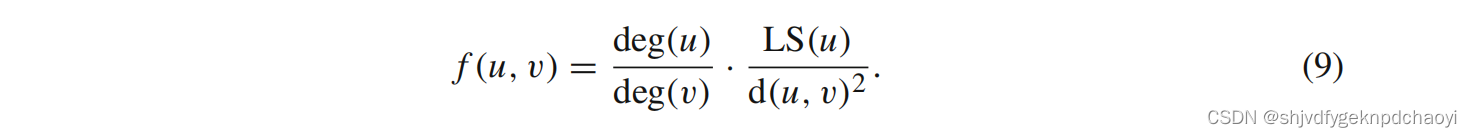 万有引力计算公式 :
万有引力计算公式 :
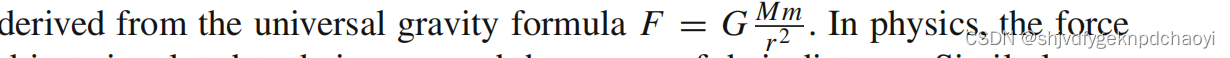
- 节点的领导力效应就像重力中某些主体的质量效应一样:领导力LS(u) 越强,影响力越大。
- 此外,我们使用了基于重力公式形式的距离平方。
- 此外,考虑到节点度在社会组织中也发挥着重要作用,我们考虑了节点度。
与重力不同,引力是有向的,因为一个节点对其领导能力更强的邻居的影响小于邻居对其的影响,因此f (u, v)可能不等于f (v, u),因此我们在公式中使用它们度数的商。
模型
- 每个节点倾向于附加到其本地领导,构建多个依赖树。
所有这些依赖树组成一片森林。 - 然后采取一个合并步骤来合并一些微小的分支。
- 最后,我们将森林中的每棵树作为一个社区,树的根节点作为相应集群的leader。
1. 确定地方领导人
第一个阶段的目标是从其邻居中识别每个节点的本地领导者。
为了检测社区结构和社区领导,提出了一种新的度量方法-领导力(创新概念1.)来量化复杂网络中节点的领导能力。
拥有更大的领导力是成为另一个关联节点的领导者的先决条件之一。
对于一个节点u,为了在它的结构邻域中找出它的局部领导者,还需要考虑链接的强度。
-
可能存在多个领导大于LS(u)(领导力,创新概念1.)的候选节点。
-
考虑到网络结构复杂,边(u, v)可能是位于两个社区之间的桥,即节点u可能在一个集群的边界,而节点v属于另一个集群。
在这种情况下,节点v不能是节点u的leader,即使LS(v) > LS(u)。【条件一】 -
因此,务必确保节点及其潜在的本地领导位于同一个集群中。
为了解决这一问题,提出了边缘紧性EC(u,v)(创新概念2.)的概念。 -
引理3.1表明判断边缘紧性是确定聚类属性的必要条件。
领导权和边缘紧致度的要求可以过滤出合理的潜在的局部领导权节点。
但满足要求的节点可能不止一个。
例如,在图3中,节点13和17都可能是节点14的本地leader,因为它们的leader值很高,且边缘紧致度值非负。【条件二】
那么如何从这些候选人中选出唯一的一位地方领导人呢?
我们应该进一步努力为每个节点识别本地领导者。 -
提出了引力(创新概念3.)
对于图1中的节点14,我们需要从候选节点13和节点17中判断哪一个是更好的leader。
由于引力f (13,14) > f(17,14),故将节点13视为节点14的本地leader。【条件三】
根据上面的定义,现在可以确定每个节点的local leader。
- (本地领导) 对于图G = (v, E)中的节点v,定义节点v选择遵循的本地领导为:
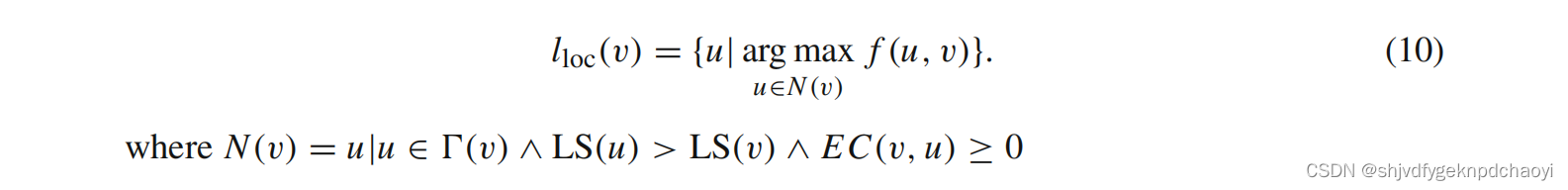
对于一个节点v,为了从v的邻域(v)中识别出它的本地领导节点,我们需要考虑三个方面。
1) 首先,我们可以知道它的局部领导u应满足LS(u) > LS(v) 领导力(创新概念1.)
其次,根据引理3.1,领导者-追随者关系应该在同一个集群中;
2) 因此,潜在的本地领导节点u应满足EC(u, v)≥0 边缘紧性(创新概念2.) 的要求。
因此,经过以上两个步骤,才能选出合格的领导候选人。
3) 最后,我们选择对节点v的引力最大的节点(创新概念3.) 作为v的局部前导。
例如,在图1中,节点4的局部前导为节点6,因为它们的边紧度EC(4,6) > 0和节点6在其邻域中对节点4的吸引力最强。
2. 构建依赖树
由于根据 (本地领导) 定义可以确定每个节点的local leader,所以扫描网络中所有节点后,就会出现初始的聚类结构。
每个节点都有一个指针,以级联方式指向其本地领导节点;
对地方领导人来说也是如此。
然后我们可以得到原始的依赖树。
- (依赖树) 图G = (V, E)中的依赖树由节点和边组成,其中树中的每个节点只有一个出口链接指向它的本地领导,除了树的根。
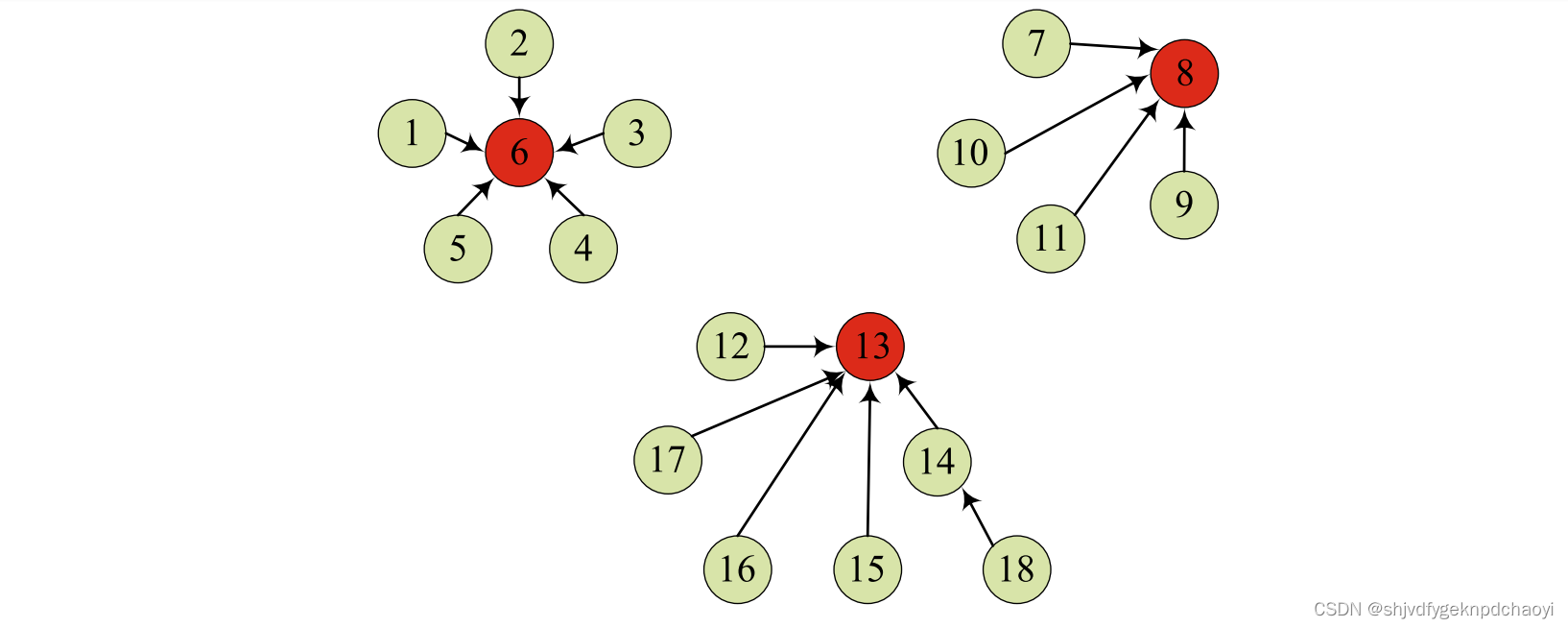
(每个节点连接到其本地领导节点后有三棵依赖树。
节点6、8和13是根节点,它们也是社区的领导者)
定理3.1 :如果lloc(u) = v和lloc(v) = w,则节点u、v和w在同一个集群中。
定理3.1表示依赖树中的所有节点都在同一个集群中。
当所有节点上的进程结束时,就会出现初步的聚类结果。
我们可以看到,每棵树代表一个集群。
图1中,红节点6,8和13为根节点,也是对应小区的leader。
此外,依赖树的结构清晰地揭示了群落的形成过程。
然而,在现实中,网络中通常存在许多噪声边;
因此,合并阶段是必要的。
算法Autoleader的伪代码描述在算法1中。
3.合并分支
在构建所有的依赖树之后,初始的社区结构被揭示出来。
然而,由于我们只是利用局部信息来确定每个节点的属性,可能存在一些微小的分支被错误地分离出来。
因此,为了获得更精确的结果,尤其在网络结构非常复杂的情况下,合并是必要的。
因为每个节点都选择了它的本地领导,所以我们只需要考虑树的这些根节点。
步骤如下:
- 如果根节点没有任何追随者(即,它是一个孤立节点),让根节点连接到在其邻居中具有最大领导权的节点。
- 如果存在多个具有最大领导权的邻居,则选择度最大的邻居作为其本地领导。
- 如果领导度最大的邻居也具有相同的程度,我们将随机选择一个。
在这里,我们只考虑非重叠的社区,所以简单地根据领导层选择一个是合理的。
对于第二种情况,解决方案有点复杂。
事实上,这种情况更为常见。
如果有一个围绕领导者形成的社区,而局部密集子图距离领导者 {6} 较远 {3 1 2 13 14},则局部密集子图中的节点将由其中领导能力最强的节点领导 {3} 。
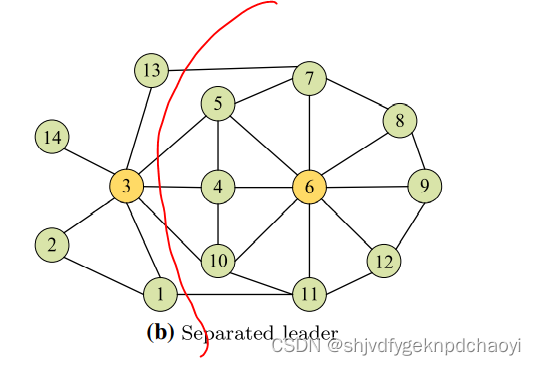
这个节点 {3} 没有直接连接到前面提到的leader,而且它不能附加到社区内的任何其他节点,因为它的leader值比leader节点小。
因此,局部密集子图往往被视为一个单独的聚类。
但子图实际上是围绕leader形成的社区的一部分,因为它与社区中的其他节点紧密相连。
例如,图5b绘制了一个玩具网络。
经过前面的步骤,我们可以得到两个初始集群{1,2,3,13,14}和{4,5,6,7,8,9,10,11,12},其中节点3和节点6是响应社区的leader。
然而,我们很容易发现,这两个簇之间的边比{1,2,3,13,14}簇中的边要多。
因此,在现实中,两个小集群应该合并成一个社区。
下面介绍如何更新初始领导节点
-
(候选集) 节点v的候选集是它的邻居满足相似性约束条件的子集:
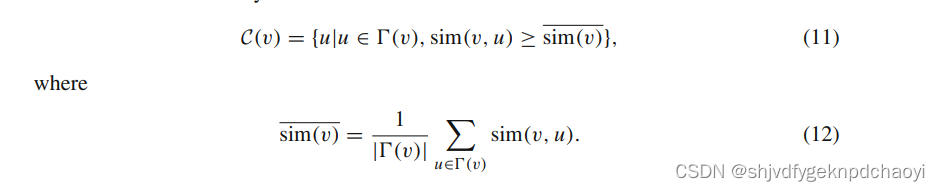
-
(更新的本地领导) 对于一个领导节点v,定义其更新的本地领导
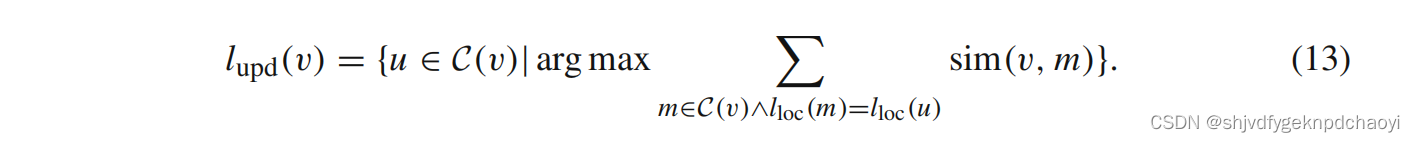
根据候选集合,我们需要从候选集合中进行选择,以确定是否应该更新初始领导节点。
对于一个leader节点v,通过扫描其 候选集C(v) 的局部leader,我们可以计算这些候选节点的唯一局部leader的权重。
1). 候选节点的初始化节点是节点v的两跳邻居,或者仅仅是节点v本身。
对于leader 3,由于相似性限制,其候选集为{1,2,4,5,10}。
2). 唯一leader的权重等于节点v与本地leader正好为l的候选节点的相似度之和,
候选节点4,5和10都是本地领导6的追随者,因此6的权重等于sim(3,4)、sim(3,5)和sim(3,10)的相似度之和。
3). 然后按降序排序,选择权重最大的leader p。
毫无疑问,根据节点3的候选集,本地leader 6是权重最大的。
因此,节点3需要更新自己的本地leader。
它可以从节点{4,5,10}中随机选择一个跟随,从而形成小分支的内聚。
4). 如果节点p恰好是节点v,则不需要更新leader节点v。如果不是,最后,节点v可以从候选集中随机选择一个节点u作为更新的本地leader,只要u的本地leader是p。形式化定义如下
对于leader 6,我们可以发现自己是权重最大的那个,这意味着不需要改变节点6的leader角色。
算法优点
-
Order-independency 顺序无关性:对于图G中的每个节点u,其本地leaderlocleader(u)是唯一的。因此,最终的社区结构是由依赖树唯一决定的。
访问节点的顺序对结果没有影响。
订单无关属性使Autoleader算法可并行,因为仅需要局部结构信息来识别局部leader。 -
Fast inquiry快速查询性:对于一个图G(V, E)和两个节点u和V,我们的Autoleader算法仅利用局部拓扑结构,不需要揭示所有的社区信息,就可以快速确定这两个节点是否在同一个集群中。
我们需要做的就是分别从两个节点u和v开始,沿着它们的本地前导指针,直到到达根结点。
如果它们的根是相同的,那么毫无疑问这两个节点在同一个集群中。
否则,节点u和v不能同时是一个组的成员。
利用该方法,无需对整个图进行分割,就可以快速识别复杂网络中不同节点的社区属性。 -
(人工合成网络) 不存在分辨率极限问题
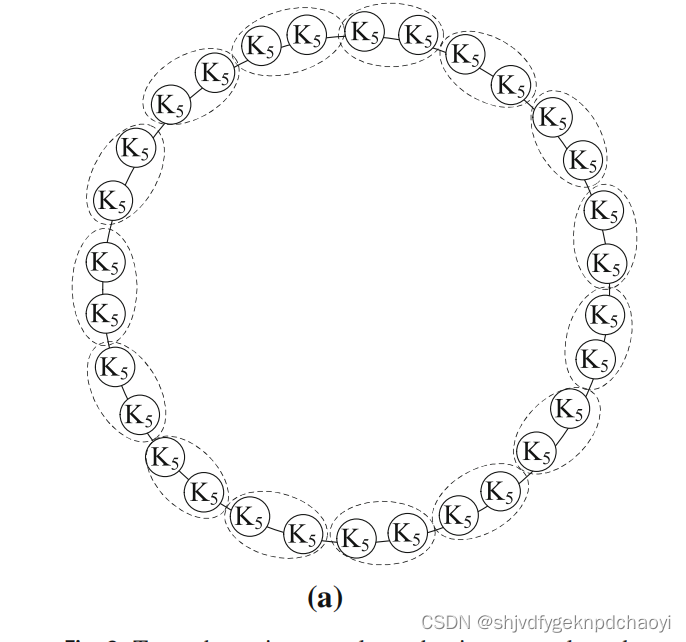
- 该图为环形网络,是由由单链路连接的相同派系Kn组成的环形网络
每个圆表示一个包含n个节点和n(n−1)/2个链接的完整图Kn。
图8a显示了一个由通过单一链接连接若干个小团体Kn组成的网络。
环网络中每个小团体都是一个社区,环网络的NMI和ARI值都为1.0。
若采用模块化优化方法,则社团检测结果会将成对的连续派系Kn视为单个群体(如虚线所示)。
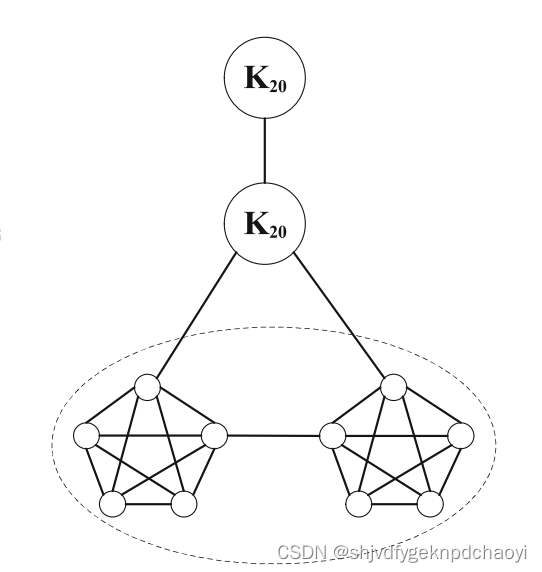
- 该图为成对网络,是由四个派系Kn组成的成对网络
1)若采用最大模块化方法,则对应于两个较小派系合并的分区(用虚线表示)。
2)然而,我们的算法Autoleader可以揭示准确的社区,并克服问题。
成对的网络中,我们还发现每个小团体都是一个社区。
NMI和ARI的结果也都是1.0。
派系之间的单一链接的边缘紧致性非常弱,以致于两个相邻的派系无法合并成一个共同体。
实验
在本节中,我们将与几种代表性的社区检测方法 (Louvain、FastModularity、LPA和SCAN) 进行比较,评估我们算法在合成数据集和真实数据集上的性能。
- 对于Louvain&SCAN,使用默认参数进行实验。
- 对于其他FastModularity&LPA,选择最好的结果进行比较。
- 对于Autoleader,参数λ被设置为0.5。
所有实验都在3.3 GHz CPU和32.0 GB RAM的工作站上进行
指标
为了定量比较不同社区检测方法的结果,我们采用了几种通常用于聚类评估的度量。
- 当网络的ground truth可用时(放到机器学习里面,再抽象点可以把它理解为真值、真实的有效值或者是标准的答案。),用 NMI (normizized Mutual Information 标准化的相互信息)、ARI (Adjusted Rand Index)和聚类纯度来衡量性能。
- 当网络的社区结构未知时,采用 the popular measure modularity ([29]: Newman ME (2006) Modularity and community structure in networks )
人工合成网络
并使合成网络与真实网络更加一致,应用了LFR基准网络,其中节点度大小和社区大小的分布可以很容易地由用户定义。
我们可以通过调节混合参数μ来控制社团检测的难度。
我们生成几个合成网络,分别包含10,000和100,000个节点。
对于每种类型的图,平均度是固定的,而混合参数μ在0.1 ~ 0.8之间。
用“S”和“B”标记的两种网络生成了不同的社区规模范围,其中“S”表示数据集中的社区规模相对较小,“B”表示社区规模相对较大。
不同算法的NMI和ARI性能分别如图6和图7所示。
这里显示的所有数值结果都是LFR基准图的十种实现所得到的平均值。
一般情况下,网络的混合参数μ越高,越难以实现社团检测。
因此,我们可以在所有这些图中看到随参数μ的增加而下降的线。
- 从图中可以看出,当混合参数不大于0.4时,SCAN和Autoleader都能获得很好的聚类效果。
- 随着参数μ的增大,其性能开始下降。
- FastModularity在大多数情况下表现最差。这是因为FastModularity基于模块化优化,并且倾向于找到较大的社区,这将*
导致分辨率限制的问题*。 - 此外,当网络中
含有大量噪声时,LPA无法发现社区结构。
因此,当参数μ > 0.7时,LPA的NMI和ARI值均为0。 - 对于BGLL,其性能随混合参数的增大而缓慢下降。
但是当网络划分变得非常困难时,BGLL的性能会急剧下降。 - 至于SCAN方法,也存在
边缘噪声的问题。
此外,为了获得更好的结果,SCAN的两个用户自定义参数不便于调优。
根据每条曲线的变化趋势,我们可以得出结论,我们的算法Autoleader的性能优于SCAN, FastModularity和bglll。
真实网络
我们选择了三个经常使用的真实世界网络进行实验。
采用NMI、ARI和Purity等指标评价方法的准确性。