1、改进transformer不擅长处理超长的序列的问题：输入u到状态x

        序列数据一般都是离散的数据 比如文本、图、DNA，但现实生活中还有很多连续的数据，比如音频、视频，对于音视频这种信号而言，其一个重要特点就是有极长的context window，而在transformer长context上往往会失败，或者注意力机制在有着超长上下文长度的任务上并不擅长。

         RNN 被诟病的一个点恰恰是 hidden state 的记忆能力有限(毕竟hidden state 的大小是固定的, 但是需要记忆的内容是随着 sequence length 增加的，用一个有限的容器去装源源不断的水流, 自然要有溢出)

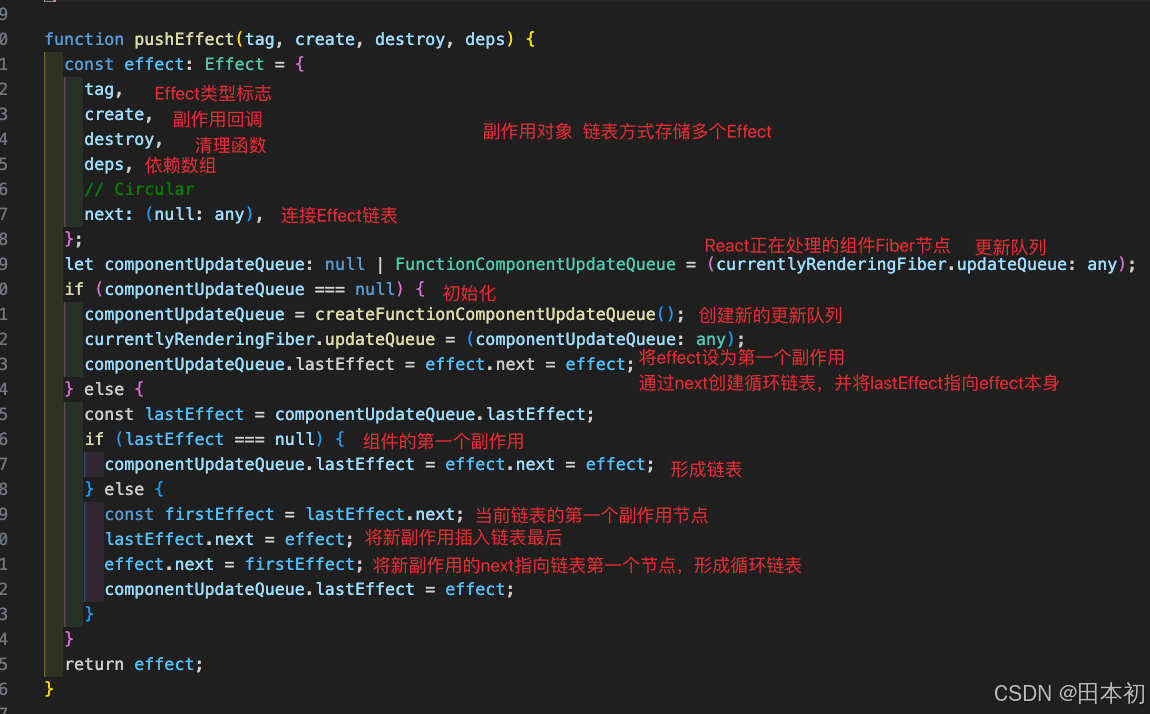
1.1 HiPPO的定义与推导：

假设 t0 时刻我们看到了原始输入信号  的之前部分，我们们希望在一个memory budget来压缩前面这一段的原始input来学习特征，一个很容易想到的方法是用多项式去近似这段input，在我们接收到更多signal的时候，我们希望仍然在这个memory budget内对整段signal进行压缩，自然，你得更新你的多项式的各项系数(这些系数一开始可以随机初始化，然后随着为了预测越发准确而对历史数据的不断更好压缩，在训练过程中调整系数的具体数值)，如下图底部所示：

HiPPO的正式定义，其为两个信号和两个矩阵的组合，HiPPO相当于将函数映射到函数，如下图所示，这里的是原始输入信号，是压缩后的信号(对应上文第一部分的状态hidden state)，而这个矩阵A就是HiPPO矩阵。

如果一条序列的长度为10000(横轴 sequence length=10000)，则代表有1万个1维的数字，那想完全表示这个序列，则需要10000unit，很明显不现实，我们考虑使用一个64unit的polynomial压缩器(相当于64个不同的hidden state，即N=64，对应A矩阵的大小为Rn*n，去表示10000unit(相当于拿 一个 64 维的向量 去记 一万个1 维的数字)，所以是非常高度的压缩。其中红色的线相当于对输入