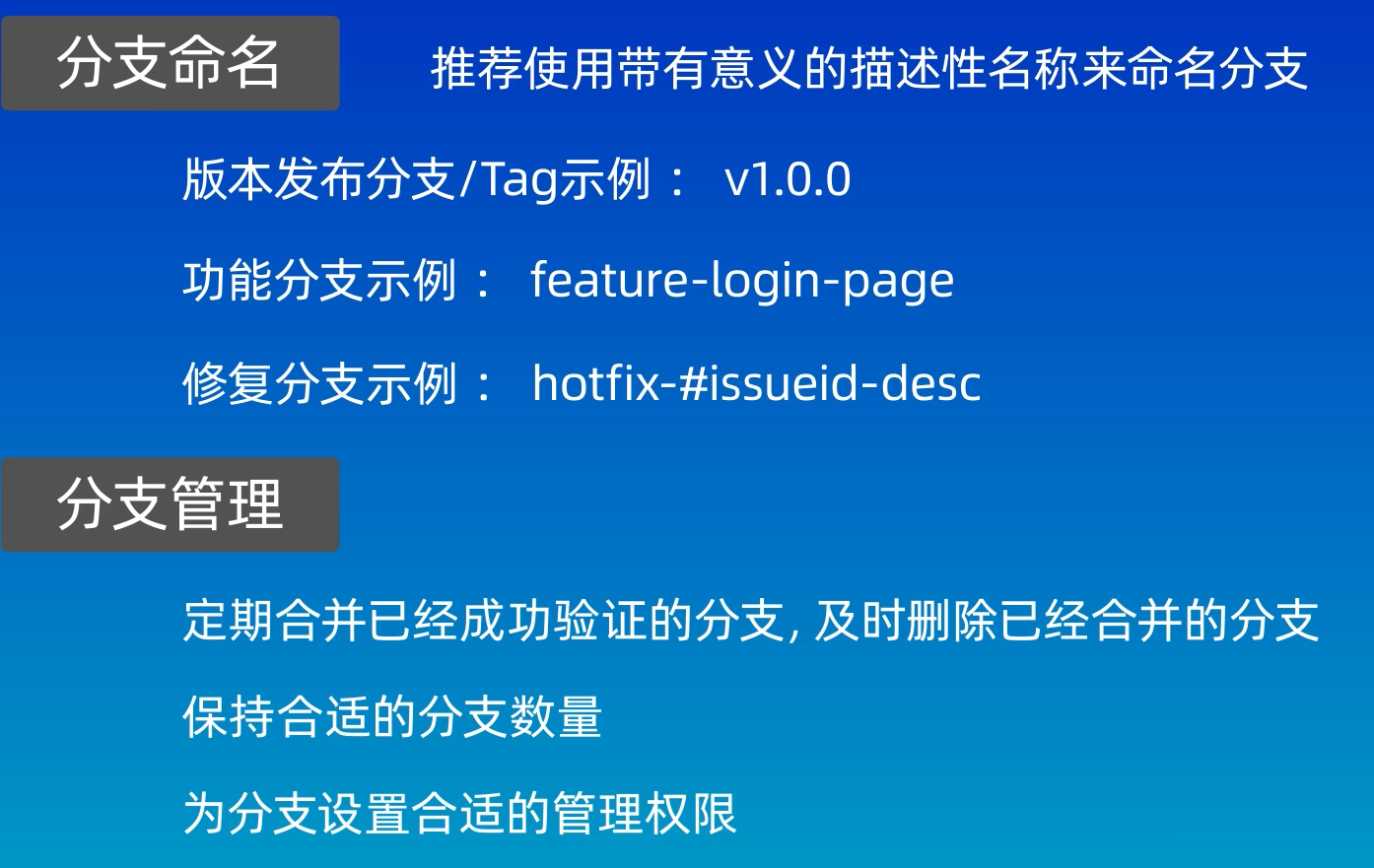
文章目录
- 一、外心法定义
- 二、习题
- 1、例题一
- 2、例题二
- 3、例题三
- 4、例题四
一、外心法定义
依然以三棱锥为例
即,找到三棱锥的外接球的球心,从而可以确定出外接球的半径R。
而三棱锥有四个顶点,这四个顶点必然都在外接球的球面上。
寻找思路:
找到底面外接圆的圆心,然后,过该圆心做垂线,那么,这个线上的点,到三个顶点的距离相等。
再找顶点到该垂线上的某个点的距离,使得该距离等于该点到底面顶点的距离。
此时,该点即为外接球的球心。
因为它到三棱锥的四个顶点的距离相等。
一般,我们把其中一个直角三角形作为底面,找它的外心。因为,直角三角形的外心必然在斜边上。

这种解法适合的题目,一般有个前提条件
1、可以找到一条线垂直某个面,那么,将该面作为底面。
可能用到的公式:
正弦定理

余弦定理

这两个定理,用于球三角形外接圆的半径。
二、习题
1、例题一

解析
我们发现,底面△ABC是一个直角三角形,所以,它的外心在斜边BC的中点。
然后,经过BC中点做垂线。
又发现面PBC⊥面ABC,所以,垂线必然在PBC平面内。
从而,变成找△PBC的外心。
由于,知道△PBC的三边长,于是,利用正弦定理和余弦定理,直接求出外接圆半径,即为三棱锥外接球的半径。

2、例题二

解析
从题目信息,可以发现△ABC是直角三角形,AC为斜边。取AC中点D。
在根据勾股定理,可以证明,PD⊥底面ABC
进而,三棱锥的外接球半径即为△PAC的外接圆半径

3、例题三

解析
发现△ACP是直角三角形,△ABP为等边三角形
在根据勾股定理,发现,△ACD也是直角三角形。
所以,AC⊥面ABP,于是,将△ABP作为底面求解。
注意,不要用Rt△ACP为底面,要用等边△ABP为底面找球心。

4、例题四

解析
以等边△BCD为底面,取BD中点T,则△ATC也是等边三角形。
所以,先找△BCD的外心,这个外心必然在CT直线上。
从而得解
为 2 13 3 \frac{2\sqrt{13}}{3} 3213





![[MyBatis-Plus]扩展功能详解](https://img-blog.csdnimg.cn/img_convert/6323b1b67cad92f3eba8e26b8402ca07.png)