910 最小差值

给你一个整数数组 nums，和一个整数 k 。

在一个操作中，您可以选择 0 <= i < nums.length 的任何索引 i 。将 nums[i] 改为 nums[i] + x ，其中 x 是一个范围为 [-k, k] 的任意整数。对于每个索引 i ，最多 只能 应用 一次 此操作。

nums 的 分数 是 nums 中最大和最小元素的差值。 

在对  nums 中的每个索引最多应用一次上述操作后，返回 nums 的最低 分数 。

示例 1：

输入：nums = [1], k = 0
输出：0
解释：分数是 max(nums) - min(nums) = 1 - 1 = 0。
示例 2：

输入：nums = [0,10], k = 2
输出：6
解释：将 nums 改为 [2,8]。分数是 max(nums) - min(nums) = 8 - 2 = 6。
示例 3：

输入：nums = [1,3,6], k = 3
输出：0
解释：将 nums 改为 [4,4,4]。分数是 max(nums) - min(nums) = 4 - 4 = 0。
 

提示：

1 <= nums.length <= 104
0 <= nums[i] <= 104
0 <= k <= 104

解题思路：先对数组排序

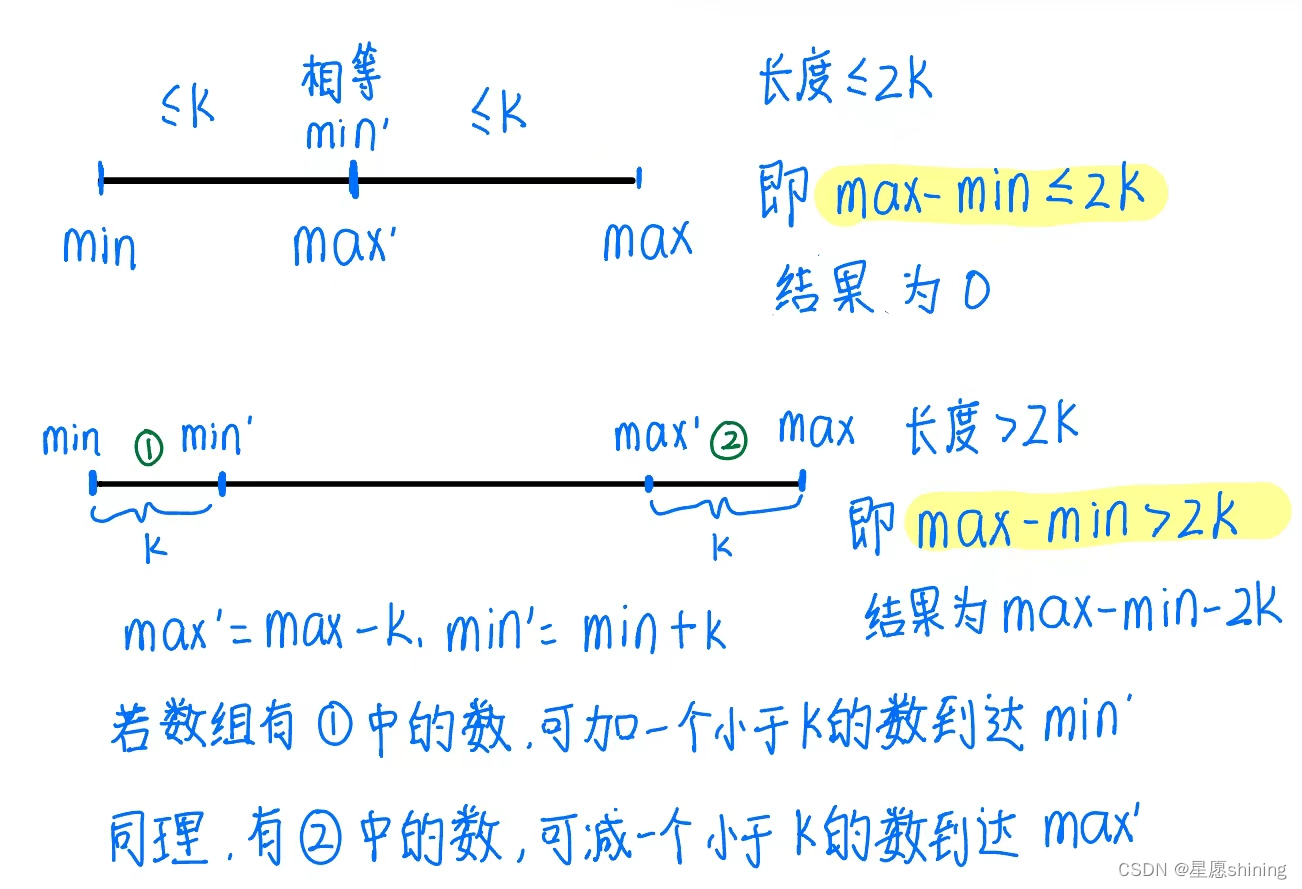
int cmp(const void *a,const void *b){return *(int*)a-*(int*)b;
}
int smallestRangeI(int* nums, int numsSize, int k) {qsort(nums,numsSize,sizeof(int),cmp);if(nums[numsSize-1]-nums[0]<=2*k)return 0;else return nums[numsSize-1]-nums[0]-2*k;
}

————————题目分界线————————

16 最接近的三数之和

给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。

返回这三个数的和。

假定每组输入只存在恰好一个解。

示例 1：

输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2)。
示例 2：

输入：nums = [0,0,0], target = 1
输出：0
解释：与 target 最接近的和是 0（0 + 0 + 0 = 0）。
 

提示：

3 <= nums.length <= 1000
-1000 <= nums[i] <= 1000
-104 <= target <= 104

解题思路：先对数组排序

int cmp(const void *a,const void *b){return *(int *)a-*(int *)b;
}
int threeSumClosest(int* nums, int numsSize, int target) {qsort(nums,numsSize,sizeof(int),cmp);int sum,close=1e7;for(int i=0;i<numsSize;i++){if(i>0&&nums[i]==nums[i-1])continue;int j=i+1,k=numsSize-1;while(j<k){int t;sum=nums[i]+nums[j]+nums[k];if(abs(sum-target)<abs(close-target))close=sum;if(sum==target)return target;if(sum>target){t=nums[k];k--;while(j<k&&nums[k]==t)k--;}else{t=nums[j];j++;while(j<k&&nums[j]==t)j++;}}}return close;
}