-
已知 f ( x ) = 1 + x + x 2 + ⋯ + x n − 1 f(x) = 1 + x + x^2 + \cdots + x^{n-1} f(x)=1+x+x2+⋯+xn−1,证明: f ( x ) ∣ [ f ( x ) + x n ] 2 − x n f(x) \mid \left[f(x) + x^n \right]^2 - x^n f(x)∣[f(x)+xn]2−xn。
x f ( x ) = x + x 2 + x 3 + ⋯ + x n xf(x) = x + x^2 + x^3 + \cdots + x^n xf(x)=x+x2+x3+⋯+xn
x f ( x ) − f ( x ) = x n − 1 xf(x) - f(x) = x^n - 1 xf(x)−f(x)=xn−1
现在计算 [ f ( x ) + x n ] 2 − x n \left[f(x) + x^n\right]^2 - x^n [f(x)+xn]2−xn:
[ f ( x ) + x n ] 2 − x n = f 2 ( x ) + 2 x n f ( x ) + x n ( x n − 1 ) = f 2 ( x ) + 2 x n f ( x ) + x n ( x − 1 ) f ( x ) = f ( x ) [ f ( x ) + x n + x n + 1 ] \begin{align*} \left [f(x) + x^n\right]^2 - x^n &= f^2(x) + 2x^n f(x) + x^n(x^n - 1) \\ &= f^2(x) + 2x^n f(x) + x^n(x - 1)f(x) \\ &= f(x) \left [f(x) + x^n + x^{n+1}\right] \end{align*} [f(x)+xn]2−xn=f2(x)+2xnf(x)+xn(xn−1)=f2(x)+2xnf(x)+xn(x−1)f(x)=f(x)[f(x)+xn+xn+1]
因此可以得出结论, [ f ( x ) + x n ] 2 − x n \left[f(x) + x^n\right]^2 - x^n [f(x)+xn]2−xn 是 f ( x ) f(x) f(x) 的倍数。
-
计算 n n n 阶行列式:
D n = ∣ x 1 2 − 2 x 1 x 2 ⋯ x 1 x n x 2 x 1 x 2 2 − 2 ⋯ x 2 x n ⋮ ⋮ ⋱ ⋮ x n x 1 x n x 2 ⋯ x n 2 − 2 ∣ D_n = \left| \begin{array}{cccc} x_1^2 - 2 & x_1 x_2 & \cdots & x_1 x_n \\ x_2 x_1 & x_2^2 - 2 & \cdots & x_2 x_n \\ \vdots & \vdots & \ddots & \vdots \\ x_n x_1 & x_n x_2 & \cdots & x_n^2 - 2 \end{array} \right| Dn= x12−2x2x1⋮xnx1x1x2x22−2⋮xnx2⋯⋯⋱⋯x1xnx2xn⋮xn2−2
记向量:
α = [ x 1 x 2 ⋮ x n ] \alpha = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} α= x1x2⋮xn
计算 D n D_n Dn 的值:
D n = ∣ α α T − 2 E n ∣ = ( − 1 ) n ∣ 2 E n − α α T ∣ = ( − 1 ) n 2 n − 1 ∣ 2 E 1 − α T α ∣ = ( − 2 ) n ( 1 − 1 2 ∑ k = 1 n x k 2 ) \begin{align*} D_n &= \left| \alpha \alpha^T - 2E_n \right| \\ &= (-1)^n \left| 2E_n - \alpha \alpha^T \right| \\ &= (-1)^n 2^{n-1} \left| 2E_1 - \alpha^T \alpha \right| \\ &= (-2)^n \left( 1 - \frac{1}{2} \sum_{k = 1}^n x_k^2 \right) \end{align*} Dn= ααT−2En =(−1)n 2En−ααT =(−1)n2n−1 2E1−αTα =(−2)n(1−21k=1∑nxk2)
进一步展开计算:
D n = ∣ 1 x 1 x 2 ⋯ x n 0 x 1 2 − 2 x 1 x 2 ⋯ x 1 x n 0 x 2 x 1 x 2 2 − 2 ⋯ x 2 x n 0 ⋮ ⋮ ⋱ ⋮ 0 x n x 1 x n x 2 ⋯ x n 2 − 2 ∣ = ∣ 1 x 1 x 2 ⋯ x n − x 1 − 2 0 ⋯ 0 − x 2 0 − 2 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ − x n 0 0 ⋯ − 2 ∣ = 1 2 ∣ 2 x 1 x 2 ⋯ x n − 2 x 1 − 2 0 ⋯ 0 − 2 x 2 0 − 2 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ − 2 x n 0 0 ⋯ − 2 ∣ = ( − 2 ) n − 1 ( 1 − 1 2 ∑ k = 1 n x k 2 ) \begin{align*} D_n &= \left| \begin{array}{ccccc} 1 & x_1 & x_2 & \cdots & x_n \\ 0 & x_1^2 - 2 & x_1 x_2 & \cdots & x_1 x_n \\ 0 & x_2 x_1 & x_2^2 - 2 & \cdots & x_2 x_n \\ 0 & \vdots & \vdots & \ddots & \vdots \\ 0 & x_n x_1 & x_n x_2 & \cdots & x_n^2 - 2 \end{array} \right| \\ &= \left| \begin{array}{ccccc} 1 & x_1 & x_2 & \cdots & x_n \\ -x_1 & -2 & 0 & \cdots & 0 \\ -x_2 & 0 & -2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -x_n & 0 & 0 & \cdots & -2 \end{array} \right| \\ &= \frac{1}{2} \left| \begin{array}{ccccc} 2 & x_1 & x_2 & \cdots & x_n \\ -2x_1 & -2 & 0 & \cdots & 0 \\ -2x_2 & 0 & -2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -2x_n & 0 & 0 & \cdots & -2 \end{array} \right| \\ &= (-2)^{n-1} \left( 1 - \frac{1}{2} \sum_{k = 1}^n x_k^2 \right) \end{align*} Dn= 10000x1x12−2x2x1⋮xnx1x2x1x2x22−2⋮xnx2⋯⋯⋯⋱⋯xnx1xnx2xn⋮xn2−2 = 1−x1−x2⋮−xnx1−20⋮0x20−2⋮0⋯⋯⋯⋱⋯xn00⋮−2 =21 2−2x1−2x2⋮−2xnx1−20⋮0x20−2⋮0⋯⋯⋯⋱⋯xn00⋮−2 =(−2)n−1(1−21k=1∑nxk2)
-
设 α i = ( a i 1 , a i 2 , ⋯ , a i n ) \alpha_i = (a_{i1}, a_{i2}, \cdots, a_{in}) αi=(ai1,ai2,⋯,ain), i = 1 , 2 , ⋯ , s i = 1, 2, \cdots, s i=1,2,⋯,s,且方程组的解满足:
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = 0 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = 0 ⋮ a s 1 x 1 + a s 2 x 2 + ⋯ + a s n x n = 0 \begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = 0 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = 0 \\ \vdots \\ a_{s1}x_1 + a_{s2}x_2 + \cdots + a_{sn}x_n = 0 \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=0a21x1+a22x2+⋯+a2nxn=0⋮as1x1+as2x2+⋯+asnxn=0
假设解还满足 b 1 x 1 + b 2 x 2 + ⋯ + b n x n = 0 b_1x_1 + b_2x_2 + \cdots + b_nx_n = 0 b1x1+b2x2+⋯+bnxn=0,记 β = ( b 1 , b 2 , ⋯ , b n ) \beta = (b_1, b_2, \cdots, b_n) β=(b1,b2,⋯,bn),证明: β \beta β 可由 α 1 , α 2 , ⋯ , α s \alpha_1, \alpha_2, \cdots, \alpha_s α1,α2,⋯,αs 线性表示。
系数矩阵为:
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a s 1 a s 2 ⋯ a s n ] , x = [ x 1 x 2 ⋮ x n ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{s1} & a_{s2} & \cdots & a_{sn} \end{bmatrix}, \quad x = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} A= a11a21⋮as1a12a22⋮as2⋯⋯⋱⋯a1na2n⋮asn ,x= x1x2⋮xn
方程组表示为:
A x = 0 Ax = 0 Ax=0
另定义扩展矩阵 B B B:
B = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a s 1 a s 2 ⋯ a s n b 1 b 2 ⋯ b n ] B = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{s1} & a_{s2} & \cdots & a_{sn} \\ b_1 & b_2 & \cdots & b_n \end{bmatrix} B= a11a21⋮as1b1a12a22⋮as2b2⋯⋯⋱⋯⋯a1na2n⋮asnbn
同样有 B x = 0 Bx = 0 Bx=0。
因为两个线性方程组同解,所以行向量组等价,即 r ( A ) = r ( B ) r(A) = r(B) r(A)=r(B)。这表示 { α 1 , α 2 , ⋯ , α s } \{\alpha_1, \alpha_2, \cdots, \alpha_s\} {α1,α2,⋯,αs} 与 { α 1 , α 2 , ⋯ , α s , β } \{\alpha_1, \alpha_2, \cdots, \alpha_s, \beta\} {α1,α2,⋯,αs,β} 的秩相等。因此, β \beta β 可以由 { α 1 , α 2 , ⋯ , α s } \{\alpha_1, \alpha_2, \cdots, \alpha_s\} {α1,α2,⋯,αs} 的线性组合表示。
-
已知 A = ( a i j ) n × n A=\begin{pmatrix}a_{ij}\end{pmatrix}_{n \times n} A=(aij)n×n 是 n n n 级正定矩阵,证明:
- a i i > 0 ( i = 1 , 2 , ⋯ , n ) a_{ii} > 0 \ (i=1,2,\cdots,n) aii>0 (i=1,2,⋯,n)
- 2 ∣ a i j ∣ < a i i + a j j ( i ≠ j ) 2 |a_{ij}| < a_{ii} + a_{jj} \ (i \neq j) 2∣aij∣<aii+ajj (i=j)
- A A A 的所有元素中绝对值最大的元素一定在主对角线上
证明 1:
记 A A A 为正定矩阵,因此存在一个 n n n 级实可逆矩阵 C C C,使得 A = C T C A = C^T C A=CTC,其中 c k i ( k = 1 , 2 , ⋯ , n ) c_{ki} \ (k=1,2,\cdots,n) cki (k=1,2,⋯,n) 不全为 0。
a i i = c i T c i = ∑ k = 1 n c k i 2 > 0 a_{ii} = c_i^T c_i = \sum_{k = 1}^n c_{ki}^2 > 0 aii=ciTci=k=1∑ncki2>0
证明 2:
c k i ( k = 1 , 2 , ⋯ , n ) c_{ki} \ (k=1,2,\cdots,n) cki (k=1,2,⋯,n) 和 c k j ( k = 1 , 2 , ⋯ , n ) c_{kj} \ (k=1,2,\cdots,n) ckj (k=1,2,⋯,n) 不全为 0,因此:
a i i − 2 ∣ a i j ∣ + a j j = c i T c i − 2 ∣ c i T c j ∣ + c j T c j = ∑ k = 1 n c k i 2 − 2 ∑ k = 1 n ∣ c k i c k j ∣ + ∑ k = 1 n c k j 2 = ∑ k = 1 n ( c k i 2 − 2 ∣ c k i c k j ∣ + c k j 2 ) = ∑ k = 1 n ( ∣ c k i ∣ − ∣ c k j ∣ ) 2 > 0 \begin{align*} a_{ii} - 2 |a_{ij}| + a_{jj} &= c_i^T c_i - 2 |c_i^T c_j| + c_j^T c_j \\ &= \sum_{k = 1}^n c_{ki}^2 - 2 \sum_{k = 1}^n |c_{ki} c_{kj}| + \sum_{k = 1}^n c_{kj}^2 \\ &= \sum_{k = 1}^n \left(c_{ki}^2 - 2 |c_{ki} c_{kj}| + c_{kj}^2\right) \\ &= \sum_{k = 1}^n \left(|c_{ki}| - |c_{kj}|\right)^2 \\ &> 0 \end{align*} aii−2∣aij∣+ajj=ciTci−2∣ciTcj∣+cjTcj=k=1∑ncki2−2k=1∑n∣ckickj∣+k=1∑nckj2=k=1∑n(cki2−2∣ckickj∣+ckj2)=k=1∑n(∣cki∣−∣ckj∣)2>0
因此, 2 ∣ a i j ∣ < a i i + a j j 2 |a_{ij}| < a_{ii} + a_{jj} 2∣aij∣<aii+ajj。
证明 3:
对任意 i ∈ { 1 , 2 , ⋯ , n } i \in \{1,2,\cdots,n\} i∈{1,2,⋯,n}, j ∈ { 1 , 2 , ⋯ , n } j \in \{1,2,\cdots,n\} j∈{1,2,⋯,n},且 i ≠ j i \neq j i=j,假设 a i i > a j j a_{ii} > a_{jj} aii>ajj,则有:
2 ∣ a i j ∣ < a i i + a j j < 2 a i i 2 |a_{ij}| < a_{ii} + a_{jj} < 2 a_{ii} 2∣aij∣<aii+ajj<2aii
因此, ∣ a i j ∣ < ∣ a i i ∣ |a_{ij}| < |a_{ii}| ∣aij∣<∣aii∣。由于 A A A 是正定矩阵,所以 a i j = a j i a_{ij} = a_{ji} aij=aji,即 ∣ a j i ∣ < ∣ a i i ∣ |a_{ji}| < |a_{ii}| ∣aji∣<∣aii∣。因此,对角线上元素的绝对值最大。
-
若 A A A 是 n n n 阶方阵,证明:
- A n = 0 A^n = 0 An=0 当且仅当 A A A 的特征值全为 0;
- A n = 0 A^n = 0 An=0,则 ∣ A + E ∣ = 1 |A + E| = 1 ∣A+E∣=1。
证明 1:
⇒ \Rightarrow ⇒
A A A 是数域 F F F 上的 n n n 级幂零矩阵,设幂零指数为 l l l,那么 A A A 的最小多项式是 λ l \lambda^l λl。
A A A 的最小多项式与 A A A 的特征多项式 f ( λ ) f(\lambda) f(λ) 在包含 F F F 的代数封闭域中有相同的根,因此 f ( λ ) = λ n f(\lambda) = \lambda^n f(λ)=λn。因此, A A A 的 n n n 个特征值均为 0。
⇐ \Leftarrow ⇐
若 A A A 的特征值为 0(重数 n n n),则 A A A 的特征多项式 f ( λ ) = λ n f(\lambda) = \lambda^n f(λ)=λn,所以 A n = f ( A ) = 0 A^n = f(A) = 0 An=f(A)=0。因此, A A A 是幂零矩阵。
证明 2:
由于 A A A 的特征值全为 0,所以 A + E A + E A+E 的特征值全为 1。因此 ∣ A + E ∣ = 1 |A + E| = 1 ∣A+E∣=1。
-
设 A = ( a i j ) n × n A = (a_{ij})_{n \times n} A=(aij)n×n 是一个 n ≥ 2 n \geq 2 n≥2 的矩阵, A ∗ A^{*} A∗ 为 A A A 的伴随矩阵,证明: ( A ∗ ) ∗ = ∣ A ∣ n − 2 A (A^{*})^{*} = |A|^{n-2} A (A∗)∗=∣A∣n−2A。
方法 1:
如果 A A A 可逆,则 A ∗ A = ∣ A ∣ E A^* A = |A| E A∗A=∣A∣E,因此 A ∗ = ∣ A ∣ A − 1 A^* = |A| A^{-1} A∗=∣A∣A−1。
( A ∗ A ) ∗ = A ∗ ( A ∗ ) ∗ = ∣ A ∗ ∣ E = ∣ A ∣ n − 1 E (A^* A)^* = A^* (A^*)^* = |A^*| E = |A|^{n-1} E (A∗A)∗=A∗(A∗)∗=∣A∗∣E=∣A∣n−1E
解得 ( A ∗ ) ∗ = ∣ A ∣ n − 2 A (A^*)^* = |A|^{n-2} A (A∗)∗=∣A∣n−2A。
如果 A A A 不可逆,即 ∣ A ∣ = 0 |A| = 0 ∣A∣=0,则存在可逆矩阵 P P P 和 Q Q Q,使得 P A Q = Λ = [ E r 0 0 0 ] PAQ = \Lambda = \begin{bmatrix} E_r & 0 \\ 0 & 0 \end{bmatrix} PAQ=Λ=[Er000],其中 r < n r < n r<n。
因此 Λ ∗ ∗ = 0 \Lambda^{**} = 0 Λ∗∗=0,从而 ( P A Q ) ∗ ∗ = P ∗ ∗ A ∗ ∗ Q ∗ ∗ (PAQ)^{**} = P^{**} A^{**} Q^{**} (PAQ)∗∗=P∗∗A∗∗Q∗∗,因为 P ∗ ∗ P^{**} P∗∗ 和 Q ∗ ∗ Q^{**} Q∗∗ 是可逆矩阵,所以 A ∗ ∗ = 0 = ∣ A ∣ n − 2 A A^{**} = 0 = |A|^{n-2} A A∗∗=0=∣A∣n−2A。
方法 2:
对于一般方阵 A A A,可取一列有理数 t k → 0 t_k \to 0 tk→0,使得 t k E + A t_k E + A tkE+A 为非奇异矩阵:
( ( t k E + A ) ∗ ) ∗ = ∣ t k E + A ∣ n − 2 ( t k E + A ) ((t_k E + A)^*)^* = |t_k E + A|^{n-2} (t_k E + A) ((tkE+A)∗)∗=∣tkE+A∣n−2(tkE+A)
注意到上式两边均为 n n n 阶方阵,其元素都是 t k t_k tk 的多项式,因此关于 t k t_k tk 连续。令 t k → 0 t_k \to 0 tk→0,即可得到结论。
-
设二次型 f ( x 1 , x 2 , x 3 ) = 2 x 1 2 + x 2 2 + x 3 2 + 2 x 1 x 2 + t x 2 x 3 f(x_1, x_2, x_3) = 2x_1^2 + x_2^2 + x_3^2 + 2x_1 x_2 + t x_2 x_3 f(x1,x2,x3)=2x12+x22+x32+2x1x2+tx2x3,回答:
- 当 t t t 为何值时,二次型 f ( x 1 , x 2 , x 3 ) f(x_1, x_2, x_3) f(x1,x2,x3) 正定?
- 当 t = 1 t=1 t=1 时,求二次型 f ( x 1 , x 2 , x 3 ) f(x_1, x_2, x_3) f(x1,x2,x3) 对应矩阵 A A A 的最小多项式 m A ( λ ) m_A(\lambda) mA(λ)。
解答 1:
对应的二次型矩阵为:
A = [ 2 1 0 1 1 t 2 0 t 2 1 ] A = \begin{bmatrix} 2 & 1 & 0 \\ 1 & 1 & \frac{t}{2} \\ 0 & \frac{t}{2} & 1 \end{bmatrix} A= 210112t02t1
A 的顺序主子式为:
H 1 = 2 , H 2 = 1 , H 3 = 2 ( 1 − t 2 4 ) − 1 = 1 − t 2 2 H_1 = 2, \quad H_2 = 1, \quad H_3 = 2 \left( 1 - \frac{t^2}{4} \right) - 1 = 1 - \frac{t^2}{2} H1=2,H2=1,H3=2(1−4t2)−1=1−2t2
因此,为了使 A A A 正定,需满足 t ∈ ( − 2 , 2 ) t \in (-\sqrt{2}, \sqrt{2}) t∈(−2,2)。
解答 2:
当 t = 1 t = 1 t=1 时,对应的矩阵为:
A = [ 2 1 0 1 1 1 2 0 1 2 1 ] A = \begin{bmatrix} 2 & 1 & 0 \\ 1 & 1 & \frac{1}{2} \\ 0 & \frac{1}{2} & 1 \end{bmatrix} A= 21011210211
计算 λ E − A \lambda E - A λE−A:
λ E − A = [ λ − 2 − 1 0 − 1 λ − 1 − 1 2 0 − 1 2 λ − 1 ] \lambda E - A = \begin{bmatrix} \lambda - 2 & -1 & 0 \\ -1 & \lambda - 1 & -\frac{1}{2} \\ 0 & -\frac{1}{2} & \lambda - 1 \end{bmatrix} λE−A= λ−2−10−1λ−1−210−21λ−1
计算 d 3 ( λ ) d_3(\lambda) d3(λ) 得:
d 3 ( λ ) = ∣ λ E − A ∣ = ( λ − 2 ) [ ( λ − 1 ) 2 − 1 4 ] + ( 1 − λ ) = ( λ − 2 ) [ λ 2 − 2 λ + 3 4 ] + ( 1 − λ ) = λ 3 − 4 λ 2 + 15 4 λ − 1 2 \begin{align*} d_3(\lambda) &= |\lambda E - A| \\ &= (\lambda - 2) \left [ (\lambda - 1)^2 - \frac{1}{4} \right] + (1 - \lambda) \\ &= (\lambda - 2) \left [ \lambda^2 - 2\lambda + \frac{3}{4} \right] + (1 - \lambda) \\ &= \lambda^3 - 4\lambda^2 + \frac{15}{4}\lambda - \frac{1}{2} \end{align*} d3(λ)=∣λE−A∣=(λ−2)[(λ−1)2−41]+(1−λ)=(λ−2)[λ2−2λ+43]+(1−λ)=λ3−4λ2+415λ−21
因此,最小多项式 m A ( λ ) m_A(\lambda) mA(λ) 为 λ 3 − 4 λ 2 + 15 4 λ − 1 2 \lambda^3 - 4\lambda^2 + \frac{15}{4}\lambda - \frac{1}{2} λ3−4λ2+415λ−21。
-
已知 A = ( 3 2 − 1 2 1 2 1 2 ) A = \begin{pmatrix} \frac{3}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{pmatrix} A=(2321−2121),求 A 100 A^{100} A100。
A = [ 3 2 − 1 2 1 2 1 2 ] = E + [ 1 2 − 1 2 1 2 − 1 2 ] = E + [ 1 2 1 2 ] [ 1 − 1 ] = E + α β T \begin{align*} A &= \begin{bmatrix} \frac{3}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix} \\ &= E + \begin{bmatrix} \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} \end{bmatrix} \\ &= E + \begin{bmatrix} \frac{1}{2} \\ \frac{1}{2} \end{bmatrix} \begin{bmatrix} 1 & -1 \end{bmatrix} \\ &= E + \alpha \beta^T \end{align*} A=[2321−2121]=E+[2121−21−21]=E+[2121][1−1]=E+αβT
由于 β T α = 0 \beta^T \alpha = 0 βTα=0,所以 ( α β T ) 2 = 0 (\alpha \beta^T)^2 = 0 (αβT)2=0,因此:
A 100 = ( E + α β T ) 100 = ∑ k = 0 100 C 100 k ( α β T ) k = E + 100 α β T = [ 51 − 50 50 − 49 ] \begin{align*} A^{100} &= \left(E + \alpha \beta^T\right)^{100} \\ &= \sum_{k = 0}^{100} C_{100}^k \left(\alpha \beta^T\right)^k \\ &= E + 100 \alpha \beta^T \\ &= \begin{bmatrix} 51 & -50 \\ 50 & -49 \end{bmatrix} \end{align*} A100=(E+αβT)100=k=0∑100C100k(αβT)k=E+100αβT=[5150−50−49]
-
设矩阵 A A A 的特征多项式 f ( λ ) = ( λ + 1 ) 3 ( λ − 2 ) 2 ( λ + 3 ) f(\lambda) = (\lambda + 1)^3(\lambda - 2)^2(\lambda + 3) f(λ)=(λ+1)3(λ−2)2(λ+3),最小多项式 m ( λ ) = ( λ + 1 ) 2 ( λ − 2 ) ( λ + 3 ) m(\lambda) = (\lambda + 1)^2(\lambda - 2)(\lambda + 3) m(λ)=(λ+1)2(λ−2)(λ+3),求:
- A A A 的所有不变因子。
- A A A 的若尔当标准型。
解答 1:
f ( λ ) f(\lambda) f(λ) 的次数为 6,说明 A A A 是一个 6 阶矩阵。最小多项式 m ( λ ) = ( λ + 1 ) 2 ( λ − 2 ) ( λ + 3 ) m(\lambda) = (\lambda + 1)^2(\lambda - 2)(\lambda + 3) m(λ)=(λ+1)2(λ−2)(λ+3),因此:
- d 6 ( λ ) = m ( λ ) = ( λ + 1 ) 2 ( λ − 2 ) ( λ + 3 ) d_6(\lambda) = m(\lambda) = (\lambda + 1)^2(\lambda - 2)(\lambda + 3) d6(λ)=m(λ)=(λ+1)2(λ−2)(λ+3)
- d 5 ( λ ) = ( λ + 1 ) ( λ − 2 ) d_5(\lambda) = (\lambda + 1)(\lambda - 2) d5(λ)=(λ+1)(λ−2)
- d 4 ( λ ) = 1 d_4(\lambda) = 1 d4(λ)=1
- d 3 ( λ ) = 1 d_3(\lambda) = 1 d3(λ)=1
- d 2 ( λ ) = 1 d_2(\lambda) = 1 d2(λ)=1
- d 1 ( λ ) = 1 d_1(\lambda) = 1 d1(λ)=1
所以, A A A 的所有不变因子为 ( λ + 1 ) , ( λ + 1 ) 2 , ( λ − 2 ) , ( λ − 2 ) , ( λ + 3 ) (\lambda + 1), (\lambda + 1)^2, (\lambda - 2), (\lambda - 2), (\lambda + 3) (λ+1),(λ+1)2,(λ−2),(λ−2),(λ+3)。
解答 2:
初等因子为 ( λ + 1 ) , ( λ + 1 ) 2 , ( λ − 2 ) , ( λ − 2 ) , ( λ + 3 ) (\lambda + 1), (\lambda + 1)^2, (\lambda - 2), (\lambda - 2), (\lambda + 3) (λ+1),(λ+1)2,(λ−2),(λ−2),(λ+3)。根据这些初等因子,可以构建 A A A 的若尔当标准型:
J = [ − 1 − 1 1 − 1 2 2 − 3 ] J = \begin{bmatrix} -1 & & & & & \\ & -1 & & & & \\ & 1 & -1 & & & \\ & & & 2 & & \\ & & & & 2 & \\ & & & & & -3 \end{bmatrix} J= −1−11−122−3
-
设 A A A 为 n n n 阶非零实矩阵, n ≥ 3 n \geq 3 n≥3,且 A T = A ∗ A^T = A^* AT=A∗。证明:
- ∣ A ∣ > 0 |A| > 0 ∣A∣>0。
- A A A 为正交矩阵。
解答 1:
由于 A T = A ∗ A^T = A^* AT=A∗,表示 A A A 为对称矩阵。因此有:
A A ∗ = A ∗ A = ∣ A ∣ E AA^* = A^* A = |A| E AA∗=A∗A=∣A∣E
因为 A T = A ∗ A^T = A^* AT=A∗,则有 A T A = ∣ A ∣ E A^T A = |A| E ATA=∣A∣E。记 B = A T A B = A^T A B=ATA, B B B 为对角矩阵,对于任意 i = 1 , 2 , ⋯ , n i = 1, 2, \cdots, n i=1,2,⋯,n 有:
b i i = ∣ A ∣ b_{ii} = |A| bii=∣A∣
进一步展开:
b i i = α i T α i = ∑ k = 1 n a k i 2 \begin{align*} b_{ii} &= \alpha_i^T \alpha_i \\ &= \sum_{k = 1}^n a_{ki}^2 \end{align*} bii=αiTαi=k=1∑naki2
由于 A A A 是非零实矩阵,故存在非零元,不妨假设为 a i j a_{ij} aij,因此 b j j = b i i = ∣ A ∣ > 0 b_{jj} = b_{ii} = |A| > 0 bjj=bii=∣A∣>0。
解答 2:
由 1 知, ∣ A ∣ > 0 |A| > 0 ∣A∣>0,说明 A A A 是可逆矩阵:
∣ A A T ∣ = ∣ A ∣ 2 = ∣ A A ∗ ∣ = ∣ ( ∣ A ∣ E ) ∣ = ∣ A ∣ n |AA^T| = |A|^2 = |AA^*| = |(|A| E)| = |A|^n ∣AAT∣=∣A∣2=∣AA∗∣=∣(∣A∣E)∣=∣A∣n
因此:
∣ A ∣ n − 2 = 1 |A|^{n-2} = 1 ∣A∣n−2=1
解得 ∣ A ∣ = 1 |A| = 1 ∣A∣=1,所以:
A A T = A A ∗ = ∣ A ∣ E AA^T = AA^* = |A| E AAT=AA∗=∣A∣E
这意味着 A T A = E A^T A = E ATA=E,即 A A A 为正交矩阵。
2024高等代数【南昌大学】
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/457510.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
iOS AVAudioSession 详解【音乐播放器的配置】
前言
在 iOS 音频开发中,AVAudioSession 是至关重要的工具,它控制着应用的音频行为,包括播放、录音、后台支持和音频中断处理等。对于音乐播放器等音频需求强烈的应用,设计一个合理的 AVAudioSession 管理体系不仅能保证音频播放…
三周精通FastAPI:16 Handling Errors处理错误
官网文档:https://fastapi.tiangolo.com/zh/tutorial/handling-errors 处理错误
某些情况下,需要向客户端返回错误提示。
这里所谓的客户端包括前端浏览器、其他应用程序、物联网设备等。
需要向客户端返回错误提示的场景主要如下:
客户端…
FastAPI、langchain搭建chatbot,langgraph实现历史记录
环境:openEuler、python 3.11.6、Azure openAi、langchain 0.3.3、langgraph 0.2.38
背景:基于FastAPI、langchain实现一个QA系统,要求实现历史记录以及存储特征信息
时间:20241022
说明:在历史记录的存储中&…
R语言机器学习算法实战系列(十四): CatBoost分类算法+SHAP值 (categorical data gradient boosting)
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍CatBoost的原理CatBoost的步骤教程下载数据加载R包导入数据数据预处理数据描述数据切割设置数据对象调节参数训练模型预测测试数据评估模型模型准确性混淆矩阵模型评估指标ROC Curv…
mysql 通过GROUP BY 聚合并且拼接去重另个字段
我的需求:
我想知道同一个手机号出现几次,并且手机号出现在哪些地方。下面是要的效果。 源数据:
CREATE TABLE bank (id bigint(20) unsigned NOT NULL AUTO_INCREMENT,user_id int(11) NOT NULL DEFAULT 0,tel varchar(255) COLLATE utf8mb4_unicode_…
【自然语言处理】BERT模型
BERT:Bidirectional Encoder Representations from Transformers
BERT 是 Google 于 2018 年提出的 自然语言处理(NLP)模型,它基于 Transformer 架构的 Encoder 部分。BERT 的出现极大提升了 NLP 任务的性能,如问答系…
Python | Leetcode Python题解之第509题斐波那契数
题目: 题解:
class Solution:def fib(self, n: int) -> int:if n < 2:return nq [[1, 1], [1, 0]]res self.matrix_pow(q, n - 1)return res[0][0]def matrix_pow(self, a: List[List[int]], n: int) -> List[List[int]]:ret [[1, 0], [0, …
自动化部署-02-jenkins部署微服务
文章目录 前言一、配置SSH-KEY1.1 操作jenkins所在服务器1.2 操作github1.3 验证 二、服务器安装git三、jenkins页面安装maven四、页面配置自动化任务4.1 新建任务4.2 选择4.3 配置参数4.4 配置脚本 五、执行任务5.1 点击执行按钮5.2 填写参数5.3 查看日志 六、查看服务器文件七…
51单片机STC8G串口Uart配置
测试环境
单片机型号:STC8G1K08-38I-TSSOP20,其他型号请自行测试; IDE:KEIL C51;
寄存器配置及主要代码
STC8G系列单片机具有4个全双工异步串行通信接口;本文以串口1为例,串口1有4种工作方式…
java疫苗发布和接种预约系统源码(springboot)
项目简介
疫苗发布和接种预约系统实现了以下功能:
疫苗发布和接种预约系统的主要使用者分为: 管理员对公告信息,医院信息,疫苗信息,医生信息,用户信息,论坛帖子信息以及预约接种信息等信息进行…
C语言程序设计:现代设计方法习题笔记《chapter5》下篇
第七题 题目分析:求最大最小值转换为条件判断问题,最大值有四种可能,最小值相应有三种情况,给出下列代码。
示例代码:
#include <stdio.h>int main() {int num1, num2, num3, num4; // 定义四个变量来存储输入…
【C++】抱C++中的函数式编程:使用`std::function`和Lambda表达式简化代码
C自C11标准引入了lambda表达式、std::function和std::bind,为开发者带来了强大的函数式编程特性。函数式编程让代码更加灵活、简洁、可重用,并使得开发者可以轻松处理回调、事件驱动编程和更复杂的函数组合。本文将详细介绍C中函数式编程的关键工具&…
解码专业术语——应用系统开发项目中的专业词汇解读
文章目录 引言站点设置管理具体要求包括: Footer管理基于URL的权限控制利用数据连接池优化数据库操作什么是数据连接池?优化的优势 利用反射改造后端代码,AJAX反射的作用及其在后端代码中的应用AJAX 实现前后端无刷新交互 引言 创新实践项目二…
Linux常用命令1
切换目录 cd
[rootlocalhost menge]# cd /[rootlocalhost /]#
cd: cd [-L|[-P [-e]] [-]] [目录]
查看当前的目录 pwd 浏览目录内容 ls ls浏览后颜色表示
白色:普通文件
蓝色:目录
红色:压缩包文件
黄色:设备文件
绿…
Python浪漫之画一个圆月亮
效果图: 完整代码:
import turtle
import time# 创建一个画布
screen turtle.Screen()
screen.bgcolor("darkblue") # 设置背景为深蓝色# 创建一个海龟(turtle)用于绘制月亮
moon turtle.Turtle()
moon.color("…
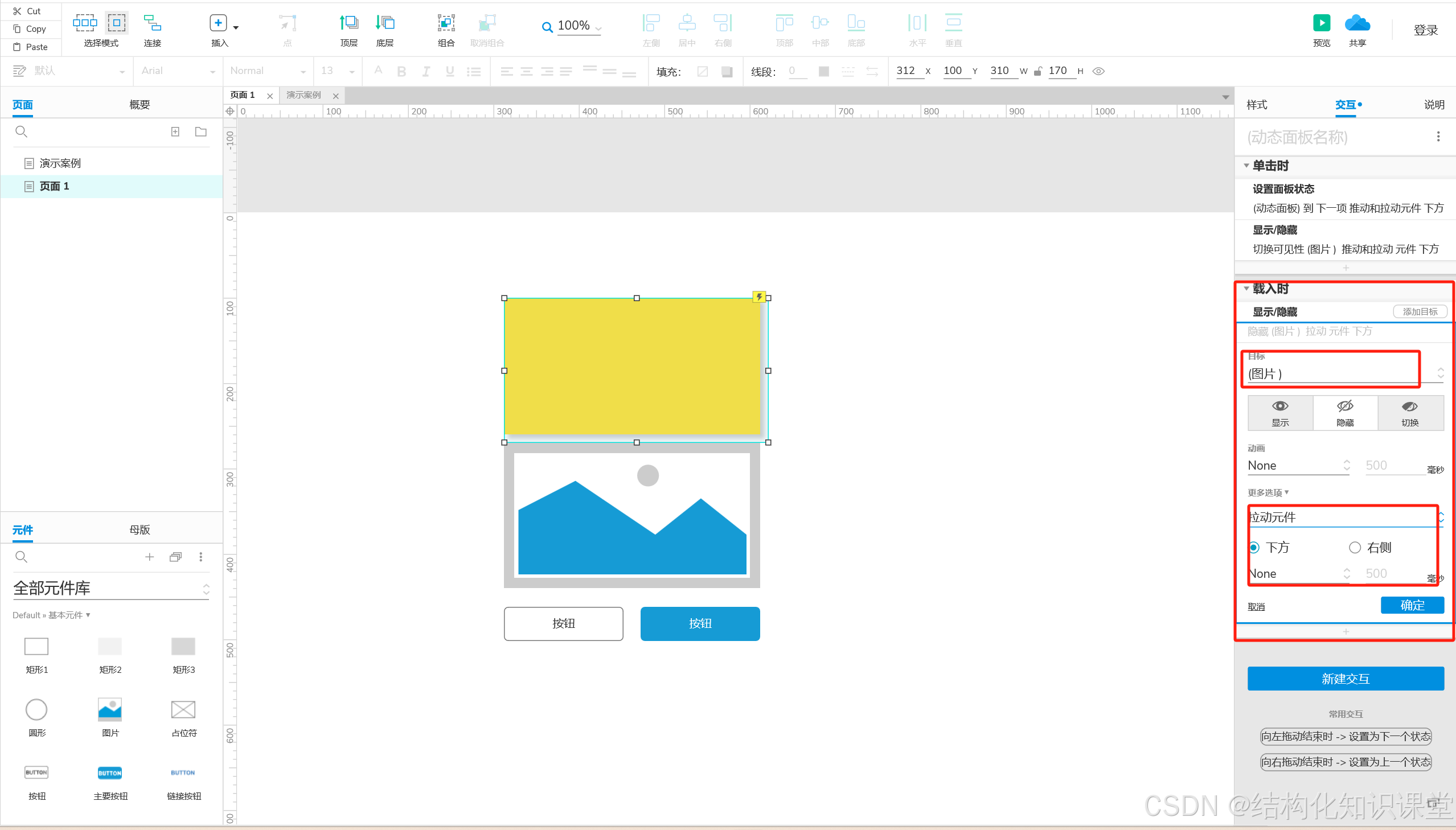
Axure设置面板状态——元件动作二
亲爱的小伙伴,在您浏览之前,烦请关注一下,在此深表感谢!因为有事断更了三天,从今天开始又回来了,继续为大家分享Axure相关知识点。
课程主题:设置面板状态
主要内容:State状态、推…
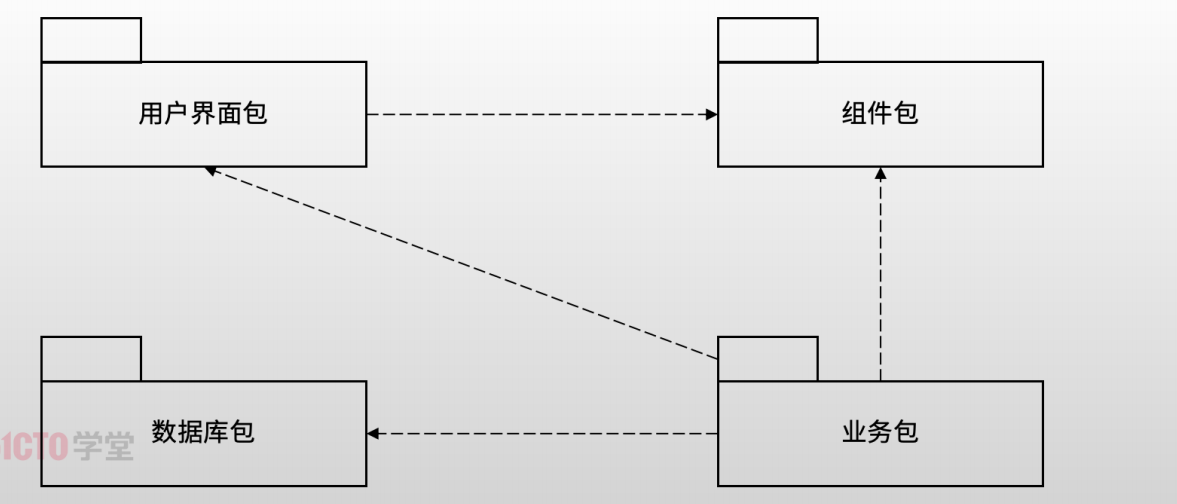
UML 总结(基于《标准建模语言UML教程》)
定义 UML 又称为统一建模语言或标准建模语言,是一种标准的图形化建模语言,它是面向对象分析与设计的一种标准表示。尽管UML 本身没有对过程有任何定义,但UML 对任何使用它的方法(或过程)提出的要求是:支持用…
springboot入门学习笔记
在我们创建了一个Springboot项目之后,我们会看到有很多文件夹和文件
Springboot程序中各类文件的意义
一.pom.xml
在 Spring Boot 项目中,pom.xml(Project Object Model)文件是 Maven 构建工具的核心配置文件。起到项目信息定义…
推荐文章
- ⭐ Unity Pico PXR_SDK转场淡入淡出
- - 工程实践 - 《QPS百万级的有状态服务实践》02 - 冷启动和热更新
- (013)window的Idea运行程序 Amazon java.nio.file.AccessDeniedException
- (1)(1.9) MSP (version 4.2)
- (GIS可视化)热力图
- (java) 进程调度
- (QT-UI)十四、在时间轴上绘制一段段时间片
- (菜鸟自学)漏洞利用——MS11-080
- (处理流)转换流与对象流
- (第75天)AutoUpgrade 升级:11GR2 到 19C
- (回溯) LeetCode 131. 分割回文串
- (生物信息学)R语言绘图初-中-高级——3-10分文章必备——饼图(初级)