一、说明
概率是支撑大部分统计分析的基本概念。从本质上讲,概率提供了一个框架,用于量化不确定性并对未来事件做出明智的预测。无论您是在掷骰子、预测天气还是评估金融市场的风险,概率都是帮助您驾驭不确定性的工具。本篇将讲授概率的原理和可操作性。
二、关键概念和示例
以下是样本空间、结果、事件和概率等关键概念的定义,以及有助于阐明每个概念的解释和示例:
2.1. 样本空间 (S)
样本空间是随机实验的所有可能结果的集合。样本空间包括实验可能出现的所有潜在结果。例如,在抛硬币时,样本空间由两个结果组成:正面和反面。
示例:
- 硬币翻转:样本空间 (S) 为 {正面、反面}。
- 掷六面骰子: 样本空间 (S) 为 {1, 2, 3, 4, 5, 6} 。
结果
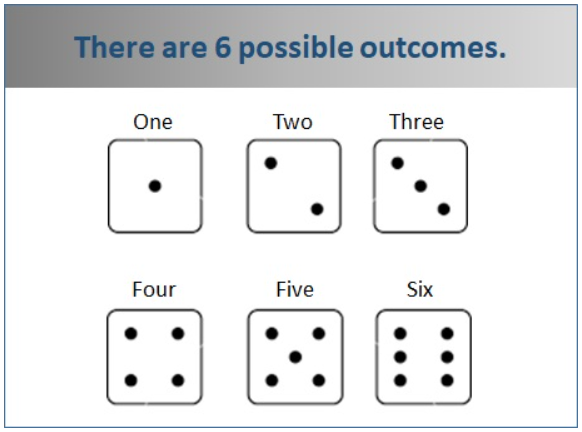
图 1.结果
结果是随机实验的单个可能结果。
结果是进行实验时发生的特定结果。样本空间的每个元素都代表一个唯一的结果。
示例:
- 硬币翻转:一种可能的结果是“正面”。
- 掷骰子:一种可能的结果是掷出“4”。
2.2 . 事件 (E)
事件是样本空间的子集,由一个或多个结果组成。
事件表示样本空间中的特定事件。它可以包括一个结果或结果的组合。事件可以用多种方式描述,例如“至少一个正面”或“掷出偶数”。
例:
- 抛硬币:事件可以是“正面朝上” E = {正面}。
- 掷骰子:事件可以是“掷偶数” E = {2, 4, 6} 。
2.3 概率 (P)
概率衡量事件发生的可能性,用 0 到 1 之间的数字表示,其中 0 表示不可能,1 表示确定性。
概率量化了事件发生的几率。概率为 0 表示事件不会发生(不可能),而概率为 1 表示事件是确定的。事件 E 的概率的计算方法是将 E 的有利结果数除以样本空间 S 中的结果总数。
例:
- 抛硬币:正面朝上的概率 P(正面) = 1/2。
- 掷骰子:掷出偶数 P(偶数) = 3/6 = 1/2 的概率,因为在六种可能的结果中,有三种有利的结果(2、4、6)。
三、事件类型
在概率中,可以根据事件与其他事件的关系来定义几种不同类型的事件:
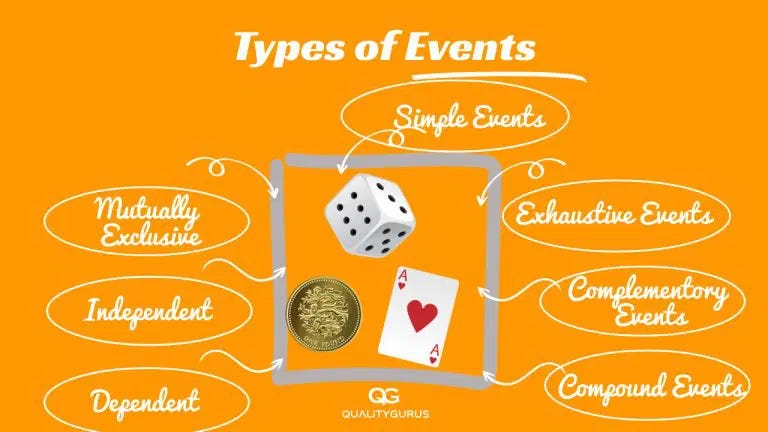
图 2.事件类型
1. 简单(或基本)事件
简单事件是指由样本空间中的一个结果组成的事件。
示例:
在一次六面骰子的掷骰中,“掷 4”事件是一个简单的事件,因为它只对应于一个结果:{4}。
2. 复合事件
复合事件是由两个或多个简单事件组成的事件。
示例:
在六面骰子的单次掷骰中,“掷偶数”事件是一个复合事件,因为它包括多个结果:{2, 4, 6}。
3. 特定事件
特定事件是保证发生的事件。它的概率始终为 1。
示例:
在六面骰子的单次掷骰中,“在 1 到 6 之间掷出一个数字”事件是确定的事件,因为掷骰子的每个结果都在这个范围内。因此,P(掷出 1 到 6 之间的数字)= 1
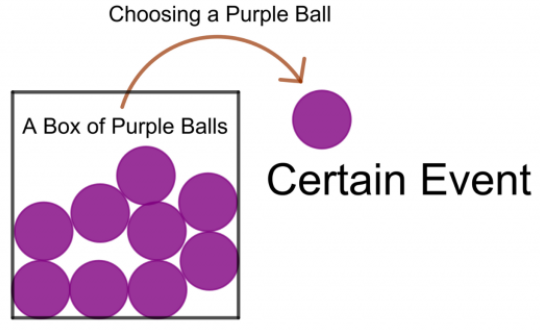
图 3.特定事件
4. 穷举事件
如果必须至少发生一个事件,则一组事件是穷举的。事件集涵盖实验的所有可能结果。
示例:
在一次六面骰子的掷骰中,{掷 1}、{掷 2}、{掷 3}、{掷 4}、{掷 5} 和 {掷 6} 的事件是详尽的,因为它们包括掷骰子的所有可能结果。他们的概率之和是 1:
P(掷 1) + P(掷 2) + P(掷 3) + P(掷 4) + P(掷 5) + P(掷 6) = 1

图 4. 穷举事件
某些事件和详尽事件之间的主要区别
- Certain Event:
— 指保证发生的单个事件。
— 事件的概率为 1。- Exhaustive Events(穷举事件):
— 指一组多个事件,这些事件共同包含实验的所有可能结果。
— 穷举集中所有事件的概率之和为 1。
5. 不可能的事件
不可能的事件是不可能发生的事件;它的概率为 0。
示例:
在单次掷出六面骰子时,“掷 7”事件是不可能的事件,因为没有与掷 7 相对应的结果。
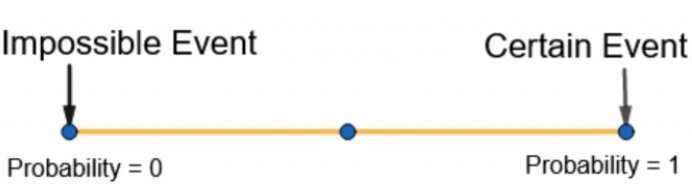
图 5.不可能和某些事件
6. 互斥(或不相交)事件
互斥事件是指不能同时或同时发生的事件;如果一个事件发生,另一个事件就不能。
示例:
在一次六面骰子掷骰子中,“掷 3”和“掷 5”事件是互斥的,因为两者不能同时发生。这些事件的交集为空:P(3 ∩ 5) = 0。
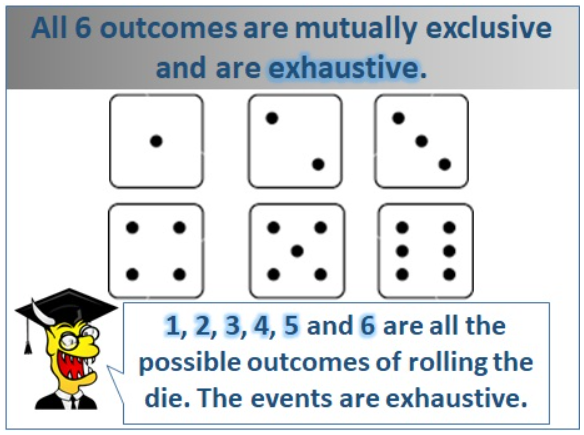
图 6. 互斥且详尽无遗
7. 非互斥事件
非互斥事件是指可以同时发生的事件;他们至少有一个共同的结果。
示例:
在一次六面骰子掷骰子中,“掷偶数”和“掷出大于 3 的数字”事件是非互斥的,因为结果 4 对两个事件都是通用的。
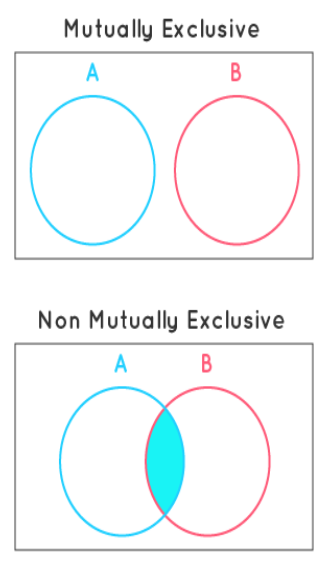
图 7. 显示互斥和非互斥的维恩图
8. 独立事件
独立事件是指一个事件的发生不会影响另一个事件发生的概率的事件。
示例:
在两个独立的实验中,抛硬币和掷骰子,“flipping faces”和“rolling a 4”这两个事件是独立的。翻转正面的概率是 1/2,掷出 4 的概率是 1/6;P(头 ∩ 4}) = 1/2 × 1/6 = 1/12。
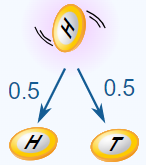
图 8. 独立活动
硬币之前“不知道”它曾出现过正面朝上。
而每一次抛硬币都是一个完美的孤立事物。
所以概率 = 1 / 2 = 0.5
9. 相关事件
相关事件是指一个事件的发生会影响另一个事件发生的概率的事件。
示例:
假设您想找到在第二次抽牌时抽到 A 的概率,假设抽到的第一张牌是 K。
- 第一次抽奖:
- 最初牌组中有 52 张牌。
- 第一次抽到 K 的概率为 4/52 = 1/13
2. 第二次抽奖(无替换):
- 如果先抽出 K,则现在牌组中还剩下 51 张牌。
- 牌组中还有 4 张 A。
- 假设先抽出 K,则在第二次抽中 A 的概率为 4/51。
“先抽 K”和“后抽 A”这两个事件是相关的,因为移除 K 会改变牌组的组成,从而影响接下来抽到 A 的概率。
10. 互补事件
互补事件是指一个事件的发生意味着另一个事件不会发生的两个事件。它们的概率之和为 1。
示例:
在一次六面骰子的掷骰中,“掷出 4”和“不掷 4”事件是互补的。如果 A 是“掷出 4”的事件,那么 Ac(A 的补数)是“不掷 4”。P(A) + P(Ac) = 1
11. 条件事件
条件事件是其概率取决于另一个事件发生的事件。
示例:
在一副 52 张牌中,如果已经抽到一张红牌,抽到红桃的概率是一个条件概率。如果 A 抽到红牌,B 抽到红桃,则 P(B|A) 是抽到红牌的情况下抽到红桃的概率。
四、概率规则:
- 联合规则:
两个事件并集的一般公式(无论它们是互斥的还是独立的)为:
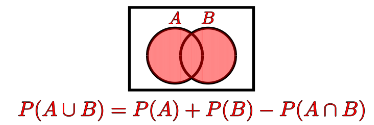
图 9. 联盟
此公式考虑了两种情况:
- 在互斥事件的情况下,其中 P(A ∩ B) = 0,公式简化为 P(A ∪ B) = P(A) + P(B)
- 在独立事件的情况下,其中 P(A ∩ B) = P(A) × P(B),公式也是 P(A ∪ B) = P(A) + P(B) + P(A) × P(B)
2. 交叉规则:
- 对于互斥事件,其中 P(A ∩ B) = 0
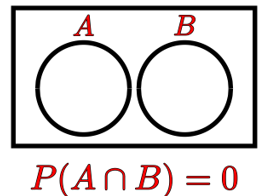
图 10. 当两个事件 A 和 B 是互斥事件时的交集规则
- 在独立事件的情况下,其中 P(A ∩ B) = P(A) × P(B),公式也是 P(A ∩ B) = P(A, B) = P(A) × P(B)
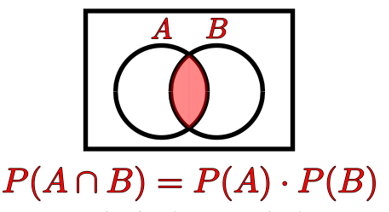
图 11. 两个事件 A 和 B 独立时的交集规则
示例:抛硬币并得到正面,然后掷骰子并获得 4 的概率是 1/2 × 1/6 = 1/12。
3. 互补规则
事件未发生的概率等于 1 减去事件发生的概率。
公式:P(Ac) = 1 − P(A)
如果 A 是事件,则 Ac (A 补码) 是 A 未发生的事件。事件的概率与其补数之和始终为 1。
示例:如果今天下雨的概率为 P(雨)=0.3,则不下雨的概率为:P(无雨)= 1−P(雨)= 1−0.3 = 0.7
五、结论
在第 17 讲,我们介绍了样本空间、结果、事件和概率等关键概念,讨论了 11 种类型的事件,并探索了基本的概率规则,包括加法、乘法和互补规则。在即将发布的博客文章。