Day41 | 动态规划：完全背包应用完全平方数单词拆分（类比爬楼梯）

Day41 | 动态规划：完全背包应用完全平方数&&单词拆分（类比爬楼梯）

动态规划应该如何学习？-CSDN博客

01背包模板 | 学习总结-CSDN博客

完全背包模板总结-CSDN博客

难点：

代码都不难写，如何想到完全背包并把具体问题抽象为完全背包才是关键

文章目录

Day41 | 动态规划：完全背包应用完全平方数&&单词拆分（类比爬楼梯）
- 279.完全平方数
- - 思路分析：
  - 1.回溯法
  - 2.记忆化搜索
  - 3.动态规划
  - 4.滚动数组
- 139.单词拆分(类比爬楼梯)
- - 思路分析：
  - - 类比爬楼梯
    - 而本题中呢
    - 难理解的点：||dp[i]的作用
  - 1.回溯法
  - 2.记忆化搜索
  - 3. 1:1翻译为动态规划

279.完全平方数

279. 完全平方数 - 力扣（LeetCode）

思路分析：

dfs(i,c)的含义是从前i个数里面选，能凑够容量c的完全平方数的最少数量

直观想法：

n是背包的容量，物品就是1到n这些数字

w重量数组为{1,2,3,4…n}。由于根号n*根号n=n，我们加的时候还是加的这些数字的平方数而不是它本身，所以w其实就是{1,2,3…根号n}到根号n就行了，后面的数平方一下肯定比n大，也没必要加了

v价值数组全都为1，因为选一个数只能给数量加1

那就和322. 零钱兑换 - 力扣（LeetCode）一模一样了

只是那道题w是硬币的面值，而这道题是1-n这些数字本身的数值

笔者这么理解就可以写出来了，看了题解后，其实w数组更加清晰的说是：完全平方数才是他们本身的重量

{1,4,9,16,25…}这样的吗，上面的{1,2,3,4}这些可以看做是序号i，{1,4,9,16}是序号i对应的完全平方数i*i

把 1,4,9,16,⋯ 这些完全平方数视作物品重量，物品价值都是 1。由于每个数（物品）选的次数没有限制，所以本题是一道标准的完全背包问题。

和零钱兑换一样，就是选或不选i²的问题

dp[i][c]=min(dp[i-1][c],dp[i][c-i*i]);

1.回溯法

1.参数和返回值

c是背包容量，本题是前i个数的完全平方数i²要凑成的数

i是物品编号，本题的物品编号i的完全平方数就是我们的物品，所以有这两个参数就够了

int dfs(int i,int c)

2.终止条件

i等于0，说明已经没有数可以选了，我们dfs的含义是前i个数凑成c，所以0和0前面已经没有数字了

此时如果要凑成的数c是0，说明我们找到了合法的方案，返回0（因为求的是物品的个数而不是凑成的方案数量，方案数量的话返回的就是1）

否则的话说明当前的分支不是合法的方法，返回正无穷（int最大值除以2是为了防止返回值+1操作溢出）

		if(i==0)if(c==0)return 0;elsereturn INT_MAX/2;

3.本层逻辑

如果说要凑的数c已经比i²小了，那就是不选i，继续往下递归，看能不能放上i-1

如果比i²大，那就在选或不选中挑一个最小值进行返回

		if(c<i*i)return dfs(i-1,c);return min(dfs(i-1,c),dfs(i,c-i*i)+1);

完整代码：

我们传入的时候物品编号从根号n开始就好，因为要凑成n，而根号n*根号n=n，比根号n大的数的平方一定比n大

当然是超时的

class Solution {
public:int dfs(int i,int c){if(i==0)if(c==0)return 0;elsereturn INT_MAX/2;if(c<i*i)return dfs(i-1,c);return min(dfs(i-1,c),dfs(i,c-i*i)+1);}int numSquares(int n) {return dfs(sqrt(n),n);}
};

2.记忆化搜索

就是还是全都初始化为-1，每次返回前给dp赋值，碰到不是-1的那就是算过的，那就直接返回计算过的结果，不需要再次递归了

完整代码：

class Solution {
public:int dfs(int i,int c,vector<vector<int>>& dp){if(i==0)if(c==0)return 0;elsereturn INT_MAX;if(dp[i][c]!=-1)return dp[i][c];if(c<i*i)return dp[i][c]=dfs(i-1,c,dp);return dp[i][c]=min(dfs(i-1,c,dp),dfs(i,c-i*i,dp)+1);}int numSquares(int n) {vector<vector<int>> dp(sqrt(n)+1,vector<int>(n+1,-1));return dfs(sqrt(n),n,dp);}
};

3.动态规划

1.确定dp数组以及下标的含义

dp[i][j]前i个数的完全平方数i²凑成j的最少方案数量

i是物品编号

j是当前要凑的数（背包容量）

2.确定递推公式

dp[i][j]=min(dp[i-1][j],dp[i][j-i*i]+1);

3.dp数组如何初始化

在回溯中，递归终止条件是i==0&&c==0，返回0

那就是dp[0][0]就是0，其他的都是正无穷（INT_MAX/2）

4.确定遍历顺序

和完全背包一样，先遍历物品在遍历容量，从前往后遍历

完整代码：

class Solution {
public:int numSquares(int n) {vector<vector<unsigned>> dp(sqrt(n)+1,vector<unsigned>(n+1,INT_MAX/2));dp[0][0]=0;for(int i=1;i<=sqrt(n);i++)for(int j=0;j<=n;j++)if(j<i*i)dp[i][j]=dp[i-1][j];else   dp[i][j]=min(dp[i-1][j],dp[i][j-i*i]+1);return dp[sqrt(n)][n];}
};

4.滚动数组

和01背包优化一样，把第一维直接删掉就行

class Solution {
public:int numSquares(int n) {vector<unsigned> dp(n+1,INT_MAX/2);dp[0]=0;for(int i=1;i<=sqrt(n);i++)for(int j=i*i;j<=n;j++)dp[j]=min(dp[j],dp[j-i*i]+1);return dp[n];}
};

139.单词拆分(类比爬楼梯)

139. 单词拆分 - 力扣（LeetCode）

思路分析：

这道题和爬楼梯、组合总和IV基本一模一样，求的都是排列数量，只是多加了一个条件

Day40 | 动态规划：完全背包应用组合总和IV（类比爬楼梯）-CSDN博客

我们这么想，把wordDict里面的单词看做我们的物品，而把s这个字符串看做背包

类比爬楼梯

在70.爬楼梯中，我们每次从 nums 中选一个数，作为往上爬的台阶数，问爬 target 个台阶有多少种方案。70 那题可以看作 nums=[1,2]，因为每次只能爬 1 个或 2 个台阶。

dp[i]的含义就是爬上第i个台阶的方案数量

1.在那道题中

我们的代码是

dp[i]=dp[i-1]+dp[i-2]

2.如果说我们一次可以爬k个台阶，当然k要比target（要爬的总楼梯数量）小

dp[i]=dp[i-1]+dp[i-2]+dp[i-3]+....+dp[i-k]
//等价于
for(int j=1;j<=k;j++)dp[i]+=dp[i-j];

3.如果说我们一次可以爬的台阶数量是nums数组里面的，那么j就是nums[j]，上面的1-k就相当于这里的nums数组的遍历

dp[i]=dp[i-nums[1]]+dp[i-nums[2]]+dp[i-nums[3]]+....+dp[i-nums[nums.size()-1]]
//等价于
for(int j=0;j<nums.size();j++)dp[i]+=dp[i-nums[j]];

相当于，在第一种情况中

nums数组为{1,2}

在第二种情况中

nums数组为{1,2,3,…,k}

而本题中呢

我们要爬到s.size()这个台阶上，每次可以爬的台阶数量呢就是wordDict[i].size()这么多个台阶

从这里开始就和爬楼梯不同了，因为字符串s这个背包是一个有形状的背包

类似于这样

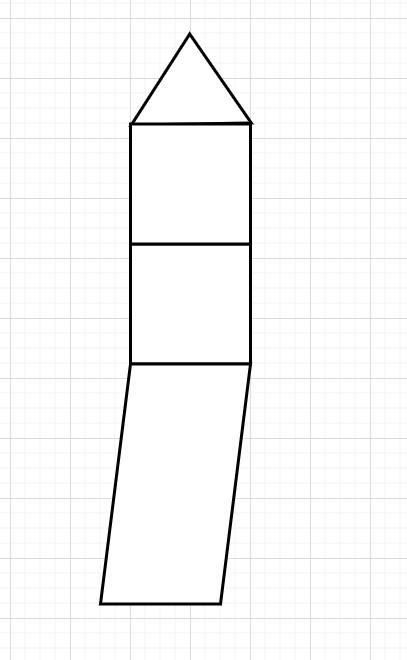
这个背包长这个倒霉样子，如果不先放平行四边形，那这个背包永远也不会装满，即使你的三角形大小为3，平行四边形可能为9

这个意思就是说，我们这次往背包里面放物品不仅仅取决于背包容量，还要看它的形状，形状那就体现在咱们要放的字符串和背包的这一截一不一样

用爬楼梯的话说就是，能爬到s.size()级台阶的方法不能只是数量大小上面达到了，你走过的路径，你选择的字符串拼起来要能组成我的s字符串才是合法的方案，才能返回true

体现在代码中就是：

爬楼梯这部分代码对应到本题，代码就会变成

for(int j=0;j<wordDict.size();j++)if(wordDict[j].size()<=i){string str;str=s.substr(i-wordDict[j].size(),wordDict[j].size());dp[i]=(str==wordDict[j]&&dp[i-wordDict[j].size()])||dp[i];}

dp[i]的含义是我们能不能用wordDict里面的字符串拼成s.begin()到s.begin()+i这个字符串，可以的话就是true，不行就是false，i是遍历背包容量

可以看到，在第一个if判断我们目前的背包可以装下这个字符串的时候，并不会立马放进去

（放进去就是(dp[i-wordDict[j].size()]，不放就是dp[i]）

而是把我们要放的字符串wordDict[i]和背包的某一截进行比较，如果一模一样的话，才会放进去

如果大家有点蒙圈的话，就再次对比一下爬楼梯，爬楼梯是看我这次爬nums[j]个台阶能不能爬到第i个台阶，这里我选这么些字符串(wordDict[j])能不能拼成s.begin()到s.begin()+i这个字符串

我可能是从第一个台阶爬两个到第三个台阶

我可能是从第二个台阶爬一个到第三个台阶

我可能是从已经拼好的部分再加上wordDict[1]就能拼成

我可能是从已经拼好的部分再加上wordDict[2]就能拼成

所以要把物品都给遍历一遍

难理解的点：||dp[i]的作用

这个是用来保留dp[i]的结果的

假如我运气好第一次循环就拼好了，dp[i]就是true，后面不管结果如果我就是true

但如果没有这个，我后面如果都没拼好过，那dp[i]就是false，就代表没有合法的方案，那这明显是错的

1.回溯法

1.参数和返回值

c是背包容量，我们要拼的字符串就是s.begin()到s.begin()+c

bool dfs(int c,string &s,vector<string>& wordDict)

2.终止条件

c==0，我们找到了合法方案，返回true

if(c==0)return true;

3.本层逻辑

这里就如上面所说，我就不过多解释了

		bool res=false;for(int i=0;i<wordDict.size();i++)if(c>=wordDict[i].size()){string str=s.substr(c-wordDict[i].size(),wordDict[i].size());res=(str==wordDict[i]&&dfs(c-wordDict[i].size(),s,wordDict))||res;}return res;

完整代码：

当然是超时的

class Solution {
public:bool dfs(int c,string &s,vector<string>& wordDict){if(c==0)return true;bool res=false;for(int i=0;i<wordDict.size();i++)if(c>=wordDict[i].size()){string str=s.substr(c-wordDict[i].size(),wordDict[i].size());res=(str==wordDict[i]&&dfs(c-wordDict[i].size(),s,wordDict))||res;}return res;}bool wordBreak(string s, vector<string>& wordDict) {return dfs(s.size(),s,wordDict);}
};

//lambda
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {function<bool(int)> dfs=[&](int c)->bool{if(c==0)return true;bool res=false;for(int i=0;i<wordDict.size();i++)if(c>=wordDict[i].size()){string str=s.substr(c-wordDict[i].size(),wordDict[i].size());res=(str==wordDict[i]&&dfs(c-wordDict[i].size()))||res;}return res;};return dfs(s.size());}
};

2.记忆化搜索

就是还是全都初始化为-1，每次返回前给dp赋值，碰到不是-1的那就是算过的，那就直接返回计算过的结果，不需要再次递归了

class Solution {
public:bool dfs(int c,string &s,vector<string>& wordDict,vector<int>& dp){if(c==0)return true;if(dp[c]!=-1)return dp[c];bool res=false;for(int i=0;i<wordDict.size();i++)if(c>=wordDict[i].size()){string str=s.substr(c-wordDict[i].size(),wordDict[i].size());res=(str==wordDict[i]&&dfs(c-wordDict[i].size(),s,wordDict,dp))||res;}return dp[c]=res;}bool wordBreak(string s, vector<string>& wordDict) {vector<int> dp(s.size()+1,-1);return dfs(s.size(),s,wordDict,dp);}
};

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {vector<int> dp(s.size()+1,-1);function<bool(int)> dfs=[&](int c)->bool{if(c==0)return true;if(dp[c]!=-1)return dp[c];bool res=false;for(int i=0;i<wordDict.size();i++)if(c>=wordDict[i].size()){string str=s.substr(c-wordDict[i].size(),wordDict[i].size());res=(str==wordDict[i]&&dfs(c-wordDict[i].size()))||res;}return dp[c]=res;};return dfs(s.size());}
};

3. 1:1翻译为动态规划

回溯终止条件为c==0的时候返回true，那动态规划dp数组初始化就是dp[0]=true

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {vector<bool> dp(s.size()+1,false);dp[0]=true;for(int i=1;i<=s.size();i++)for(int j=0;j<wordDict.size();j++)if(wordDict[j].size()<=i){string str;str=s.substr(i-wordDict[j].size(),wordDict[j].size());dp[i]=(dp[i-wordDict[j].size()]&&str==wordDict[j])||dp[i];}return dp[s.size()];}
};