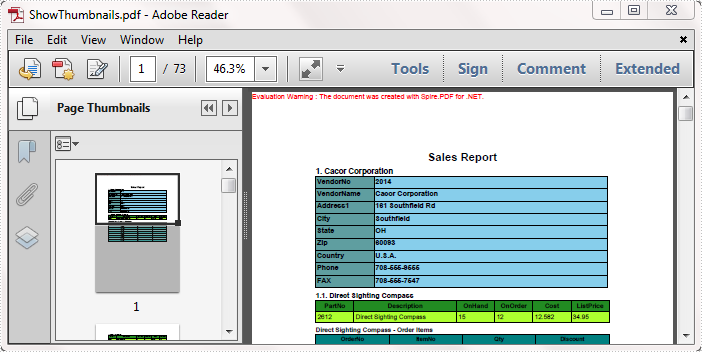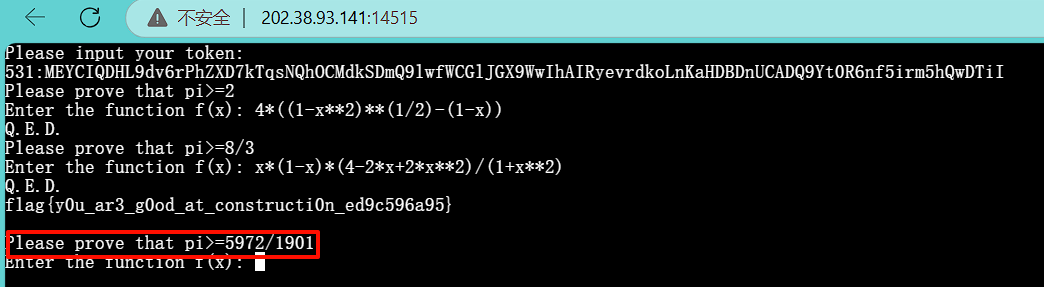
上一文《Easy》末尾出现了又要我们证明的例子,Hard难度就是继续答题答下去
其实一样可以用那篇文章https://zhuanlan.zhihu.com/p/669285539中的式子继续算下去,但是有三个系数,实在是太费时间和人力了

翻到下面的第十九种类型,可以看到一个只有两个系数的式子:

只需要π的系数为 1,常数项为负的目标有理数,且f(0)=a≥0,f(1)=a+b≥0即可
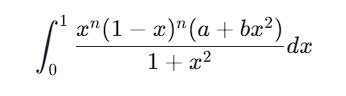
(到这里就很懵逼了,抄了大佬的代码,加上自己的token)

import numpy as np
import sympy
import pwn
import time
token= "531:MEYCIQDHL9dv6rPhZXD7kTqsNQhOCMdkSDmQ9lwfWCGlJGX9WwIhAIRyevrdkoLnKaHDBDnUCADQ9Yt0R6nf5irm5hQwDTiI"
r=pwn.remote('202.38.93.141', 14514)
time.sleep(2)
print(r.recv())
r.sendline(token)
time.sleep(2)
x,a = sympy.symbols('x,a')
eq = (-19812862426748847450700524950934251480543711738389516063357602688377780058039093204490404251005561 - 1286403201230523828226905/(-1 + a))/6306629984033528273161447763685161613920002253047080803323924073224122703966811721717856075776000for i in range(40):data = str(r.recv(),encoding='UTF-8')print(data)index1 = data.find('=')index2 = data.find('Enter')x,a = sympy.symbols('x,a')frac = sympy.sympify(data[index1+1:index2-1])aans = sympy.solve(eq+frac, a)ans = sympy.simplify(x**96*(1 - x)**96*(1 + aans[0]*x**2)/(1 + x**2)/70368744177664/(1 - aans[0]))print('----------- %d -----------' % (i+1))print(ans)r.sendline(str(ans).encode('UTF-8'))if i == 39:r.interactive()time.sleep(1)

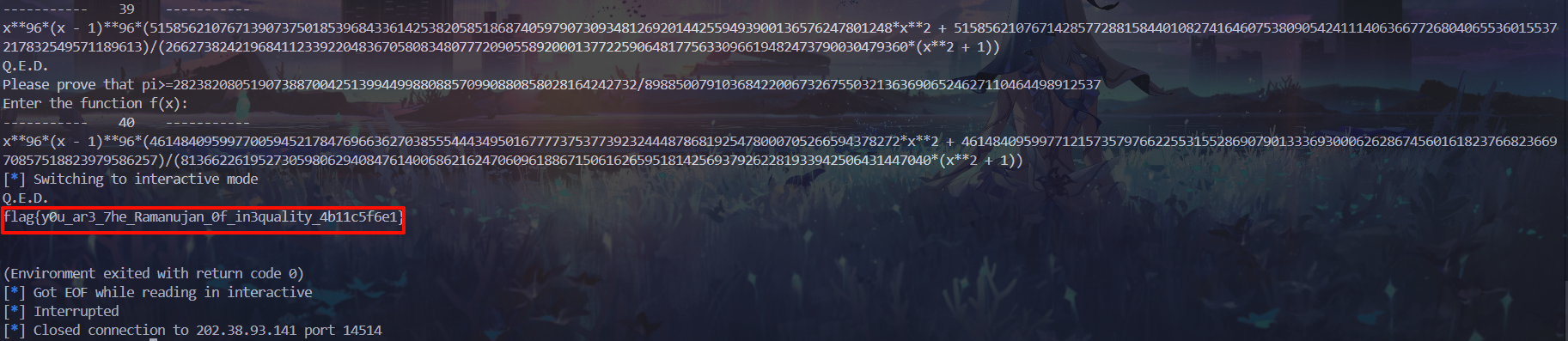
到第四十轮的时候,成功得到第二个flag