参考资源： 1.https://blog.csdn.net/zichen_ziqi/article/details/80408465
2.https://blog.csdn.net/HXG2006/article/details/79649154
3.https://blog.csdn.net/qq_32790593/article/details/84073238

1.图像分割指标

前言
在医学分割算法中，通常医生的手绘标注作为金标准（Ground Truth，简称GT），其他算法分割的作为预测结果（Rseg,简称SEG）。

分类问题
考虑一个二分类的情况，类别为1和0，我们将1和0分别作为正类（positive）和负类（negative），则实际分类的结果有4种，表格如下：
从这个表格中可以引出一些其它的评价指标：

• ACC：classification accuracy，描述分类器的分类准确率
  计算公式为：ACC=(TP+TN)/(TP+FP+FN+TN)
• BER：balanced error rate
  计算公式为：BER=1/2*(FPR+FN/(FN+TP))
• TPR：true positive rate，描述识别出的所有正例占所有正例的比例，敏感度（sensitivity）、查全率/召回率（Recall）
  计算公式为：IOU/TPR=TP/ (TP+ FN)
• FPR：false positive rate，描述将负例识别为正例的情况占所有负例的比例
  计算公式为：FPR= FP / (FP + TN)
• TNR：true negative rate，描述识别出的负例占所有负例的比例，特异度（specificity）
  计算公式为：TNR= TN / (FP + TN)
• PPV：Positive predictive value，阳性预测值、查准率（Precision）
  计算公式为：PPV=TP / (TP + FP)
• NPV：Negative predictive value，阴性预测值
  计算公式：NPV=TN / (FN + TN)

医学标准指标图

下面以医学中糖尿病人的筛查为例对敏感度和特异度进行解释。在这个例子中，我们只将病人血糖水平作为判断是否患有糖尿病的指标。下图为正常人和糖尿病患者血糖水平的统计图：

我们发现两个人群中有重叠的部分，这个时候判定标准定的不同，得到的结果就会不同。如果我们把标准定在最左边的虚线上，则低于这条线的为正常人，高于这条线的包含了两类人：正常人和糖尿病患者。这种时候就是灵敏度最高的时候，即实际有病而被诊断出患病的概率，没有放过一个患病的人。如果将标准定在最右边的虚线上，则是特异度最高的时候，即实际没病而被诊断为正常的概率，没有冤枉一个没病的人。
终上所述，敏感度高=漏诊率低，特异度高=误诊率低。理想情况下我们希望敏感度和特异度都很高，然而实际上我们一般在敏感度和特异度中寻找一个平衡点，这个过程可以用ROC(Receiver Operating Characteristic)曲线来表示：

即图中V34点，具有较高的灵敏度和特异度。

2. 两个问题

(记住我用这个程序来做) 问题1：医学图像分割领域中的模型评价指标总结

强烈建议参照以下两篇文章：

《Performance measure characterization for evaluating neuroimage segmentation algorithms》

《Metrics for evaluating 3D medical imagesegmentation: analysis, selection, and tool》

度量指标分析工具github:

1、医学图像比赛（ISBI2017或者MICCAI2007）中常用到的几个度量指标：DICE，VOE，RVD，ASD，MSD等等；如何编程实现？（Matlab代码与Python代码）

符号定义：
：代表 ground truth的分割结果
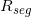：代表预测的分割结果

（1）DICE（值域为[0,1]）: 使用频率最高。数学定义如下，具体表示两个物体相交的面积占总面积的比值，完美分割该值为1。

（2）VOE（volumetric overlap error）： 与DICE类似，数学定义如下，它将and操作换成了减法操作，以此来代表错误率。

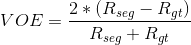
（3）RVD（relative volume difference）： 表示两者体积之间的差异，数学定义如下。

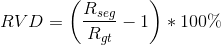
（4）ASD（average symmetric surface distance）： 先定义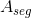代表的是预测的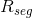中的边界的像素，同样地可以得到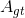的定义。然后对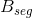的定义，同理可得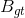的定义。那么ASD的数学定义为：


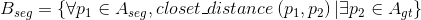
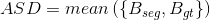
（5）MSD（maximum symmetric surface distance）：
与ASD定义比较类似，只不过把计算平均的操作替换成了计算最大值的操作。其数学定义为：

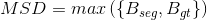
参照博客：图像分割评价标准代码
全部的分割指标MATLAB代码链接:https://pan.baidu.com/s/1u44TOhB7N0GwcyfpFUg2mQ ,提取码:9b10
内容如下：

（一）Matlab 具体的代码实现如下：

主函数demo：

clc;clear all;close all;
%% step 1：读入图像  
SEG = imread('0009_CHS.png');      % 读入分割图像
GT  = imread('0009.png');          % 读入真值图像%% step 2：灰度化
if (length(size(SEG))>2 && length(size(GT))>2)SEG = im2gray(SEG);            % 灰度化分割图像GT  = im2gray(GT);             % 灰度化真值图像
end%% step 3：二值化
SEG = imbinarize(SEG);             % 二值化分割图像
GT  = imbinarize(GT);              % 二值化真值图像%% step 4：画图预览
figure(1),
subplot(121),imshow(SEG);
title('二值化后的分割图像');
subplot(122),imshow(GT);
title('二值化后的真值图像');%% step 5：计算各个评价指标% (1)计算DICE系数
DSI = calDSI(SEG, GT);   
fprintf('(1) DICE系数：        DSI       =  %.4f\n',DSI);% (2)计算VOE系数
VOE = calVOE(SEG, GT);   
fprintf('(2) VOE系数：         VOE       =  %.4f\n',VOE);% (3)计算RVD系数
RVD = calRVD(SEG, GT); 
fprintf('(3) RVD系数：         RVD       =  %.4f\n',RVD);% (4)计算Precision系数
Precision = calPrecision(SEG, GT); 
fprintf('(4) Precision系数：   Precision =  %.4f\n',Precision);%（5）计算Recall系数
Recall = calRecall(SEG, GT); 
fprintf('(5) Recall系数：      Recall    =  %.4f\n\n\n',Recall);disp('其他评价指标的计算');
% (6)其他评价指标的计算
jaccard     = Jaccard_Index(SEG, GT)
sensitivity = getSensitivity(SEG, GT)
hd          = Hausdorff_Dist(SEG, GT)
apd         = Avg_PerpenDist(SEG, GT)
confm_index = ConformityCoefficient(SEG, GT)

其中调用函数文件分别为：
（a）calDSI函数文件：

function DSI = calDSI(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % 计算DICE系数，即DSI  DSI = 2*double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(SEG(:))) + sum(uint8(GT(:))));  
end

(b) calVOE函数文件：

function VOE = calVOE(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % 计算VOE系数，即VOE  VOE = 2*double(sum(uint8(SEG(:))) - sum(uint8(GT(:)))) / double(sum(uint8(SEG(:))) + sum(uint8(GT(:))));  
end

© calRVD函数文件：

function RVD = calRVD(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % 计算RVD系数，即RVD  RVD = double(sum(uint8(SEG(:))) ) / double(sum(uint8(GT(:)))) - 1;  
end 

(d) calPrecision函数文件：

function precision = calPrecision(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % precision  precision = double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(SEG(:))));  
end

(e) calRecall函数文件：

function recall = calRecall(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % recall  recall = double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(GT(:))));  
end 

(f) 其他指标的函数文件见以上链接。

（二）Python代码如下：

import cv2
from matplotlib import pyplot as plt# 计算DICE系数，即DSI
def calDSI(binary_GT,binary_R):row, col = binary_GT.shape  # 矩阵的行与列DSI_s,DSI_t = 0,0for i in range(row):for j in range(col):if binary_GT[i][j] == 255 and binary_R[i][j] == 255:DSI_s += 1if binary_GT[i][j] == 255:DSI_t += 1if binary_R[i][j]  == 255:DSI_t += 1DSI = 2*DSI_s/DSI_t# print(DSI)return DSI# 计算VOE系数，即VOE
def calVOE(binary_GT,binary_R):row, col = binary_GT.shape  # 矩阵的行与列VOE_s,VOE_t = 0,0for i in range(row):for j in range(col):if binary_GT[i][j] == 255:VOE_s += 1if binary_R[i][j]  == 255:VOE_t += 1VOE = 2*(VOE_t - VOE_s)/(VOE_t + VOE_s)return VOE# 计算RVD系数，即RVD
def calRVD(binary_GT,binary_R):row, col = binary_GT.shape  # 矩阵的行与列RVD_s,RVD_t = 0,0for i in range(row):for j in range(col):if binary_GT[i][j] == 255:RVD_s += 1if binary_R[i][j]  == 255:RVD_t += 1RVD = RVD_t/RVD_s - 1return RVD# 计算Prevision系数，即Precison
def calPrecision(binary_GT,binary_R):row, col = binary_GT.shape  # 矩阵的行与列P_s,P_t = 0,0for i in range(row):for j in range(col):if binary_GT[i][j] == 255 and binary_R[i][j] == 255:P_s += 1if binary_R[i][j]   == 255:P_t += 1Precision = P_s/P_treturn Precision# 计算Recall系数，即Recall
def calRecall(binary_GT,binary_R):row, col = binary_GT.shape  # 矩阵的行与列R_s,R_t = 0,0for i in range(row):for j in range(col):if binary_GT[i][j] == 255 and binary_R[i][j] == 255:R_s += 1if binary_GT[i][j]   == 255:R_t += 1Recall = R_s/R_treturn Recallif __name__ == '__main__':# step 1：读入图像，并灰度化img_GT = cv2.imread('0009.png',0)img_R  = cv2.imread('0009_CHS.png',0)# imgray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)   # 灰度化# img_GT = img_GT[:,:,[2, 1, 0]]# img_R  = img_R[:,: [2, 1, 0]]# step2：二值化# 利用大律法,全局自适应阈值 参数0可改为任意数字但不起作用ret_GT, binary_GT = cv2.threshold(img_GT, 0, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU)ret_R, binary_R   = cv2.threshold(img_R, 0, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU)# step 3： 显示二值化后的分割图像与真值图像plt.figure()plt.subplot(121),plt.imshow(binary_GT),plt.title('真值图')plt.axis('off')plt.subplot(122),plt.imshow(binary_R),plt.title('分割图')plt.axis('off')plt.show()# step 4：计算DSIprint('（1）DICE计算结果，      DSI       = {0:.4}'.format(calDSI(binary_GT,binary_R)))  # 保留四位有效数字# step 5：计算VOEprint('（2）VOE计算结果，       VOE       = {0:.4}'.format(calVOE(binary_GT,binary_R)))# step 6：计算RVDprint('（3）RVD计算结果，       RVD       = {0:.4}'.format(calRVD(binary_GT,binary_R)))# step 7：计算Precisionprint('（4）Precision计算结果， Precision = {0:.4}'.format(calPrecision(binary_GT,binary_R)))# step 8：计算Recallprint('（5）Recall计算结果，    Recall    = {0:.4}'.format(calRecall(binary_GT,binary_R)))

运行结果：

2、分割精度、过分割率、欠分割率的定义
（1）分割精度：分割准确的面积占GT图像中真实面积的百分比，数学定义如下：

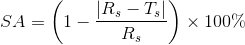
其中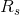表示专家手工勾画出的分割图像的参考面积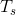，表示算法分割得到的图像的真实面积，表示错误分割的像素点个数。

（2）过分割率：即分割在GT图像参考面积之外的像素点的比率，数学定义如下：

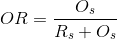
其中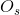表示本不应该包含在分割结果中的像素点个数，实际却在分割结果中的像素点个数。换句话讲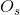，中的像素点出现在实际分割图像中，但不出现在理论分割图像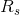中。

（3）欠分割率：即分割在GT图像参考面积之中欠缺的像素点的比率，数学定义如下：

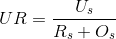
其中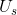表示本应该包含在分割结果中的像素点个数，实际却不在分割结果中的像素点个数。换句话讲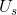，中的像素点出现在理论分割图像中，但不出现在实际分割图像中。

3、灵敏度与特异度的定义
假设实验图像为I，真实分割结果为G，实际分割结果为R。
（1）灵敏度：将实际是感兴趣区域的像素点正确地判断为感兴趣区域像素的比例，其衡量的是分割实验中能分割感兴趣区域的能力，其数学定义如下。

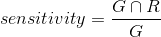
Matlab的灵敏度函数：

function sen = getSensitivity(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % sensitivity  sen = double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(SEG(:))));  
end 

（2）特异度：将实际不是感兴趣区域的像素点正确地判断为不是感兴趣区域像素的比例，其衡量的是分割实验中能正确判断不是感兴趣区域像素点的能力，其数学定义如下。

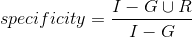
问题2：在显著性检测方面，假设现有三种方法（DSR，GMA，MCA）检测标准数据库中的部分图像（还有原图与真值图），分别得到三种结果，如何求三种方法与真值图之间的MAE（平均绝对误差），并绘制PR-curve曲线图呢？
（1）image原图

（2）mask图像 (ground truth，真值图)

（3）resultsDSR图像

（4）resultsGMA图像

（5）resultsMCA图像

文件夹内容如下图：链接https://pan.baidu.com/s/1ChxZo1OHzVUx9NtAAVPEhQ , 或PR-curve绘制，提取码:196z

输出结果：
具体实现——Matlab代码如下：

clear all;clc;close all;
addpath('Functions\');%加载文件夹Functions中的函数
%% 三种方法得到的结果路径，以及真值图路径
result1 = 'resultsDSR\';
result2 = 'resultsMCA\';
result3 = 'resultsGMR\';
mask = 'mask\';
%% 创建文件夹evaluation index，目的是保存PR曲线图
newFolder = 'evaluation index'; 
if ~exist(newFolder)mkdir(newFolder);
end
%% Evaluation index 1: evaluating MAE
resultSuffixDSR = '_DSR.png';
resultSuffixMCA = '_MCA.png';
resultSuffixGMR = '_stage1.png';
gtSuffix = '.png';maeDSR = CalMeanMAE(result1, resultSuffixDSR, mask, gtSuffix);
maeMCA = CalMeanMAE(result2, resultSuffixMCA, mask, gtSuffix);
maeGMR = CalMeanMAE(result3, resultSuffixGMR, mask, gtSuffix);
%% Evaluation index 2: ploting PR curve
[rec1, prec1] = DrawPRCurve(result1, resultSuffixDSR, mask, gtSuffix, true, true, 'r');
hold on
[rec2, prec2] = DrawPRCurve(result2, resultSuffixMCA, mask, gtSuffix, true, true, 'g');
hold on
[rec3, prec3] = DrawPRCurve(result3, resultSuffixGMR, mask, gtSuffix, true, true, 'b');
hold off;
grid on;
box on;
xlabel('Recall');
ylabel('Precision');
% title(strcat('PR-curve','  ( ',sprintf(' MAE = %1.6f ',maeDSR),' )'));
title('PR-curve');
lg = legend({'DSR method','CA method','GMR method'});
set(lg, 'location', 'southwest');
k=1.2;
set(gcf,'units',get(gcf,'paperunits'));
set(gcf,'paperposition',get(gcf,'position')*k);
saveas(gcf,strcat(newFolder,'\PR-curve','.bmp'));

3.IOU和假阳性率

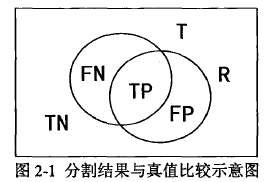
IOU：

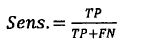
假阳性率：

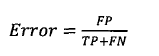
Matlab实现代码：

% 函数功能：计算两张图像的IOU
% lable_img：输入的图像A，只包含0和255像素值的图像
% res_img:输入的图像B，也同样只包含0和255像素值的图像
% 返回值：iou两张图像的iou；yl假阳性率
function [iou,yl] = Calc_IOU(lable_img, res_img)
[rows, cols] = size(lable_img);% 计算总面积
%total_area = rows * cols;% 统计lable_img、res_img中255像素值的个数
lable_area = 0; % 标记出来的面积
res_area = 0;   % 分割出来结果的面积
intersection_area = 0; % 相交区域的面积
combine_area = 0;      % 两个区域联合的面积% 开始计算各部分的面积
for i = 1: 1: rowsfor j = 1: 1: colsif lable_img(i, j)==255 && res_img(i, j)==255intersection_area = intersection_area + 1;lable_area = lable_area + 1;res_area = res_area + 1;elseif lable_img(i, j)==255 && res_img(i, j)~=255lable_area = lable_area + 1;elseif lable_img(i, j)~=255 && res_img(i, j)==255res_area = res_area + 1;endend
end
combine_area = combine_area + lable_area + res_area - intersection_area;% 得到IOU
iou = double(intersection_area) / double(combine_area);
fprintf('IOU: %f\n', iou);
% 得到假阳性率
yl = double(res_area - intersection_area) / double(combine_area);
fprintf('假阳性率为：%f\n', yl);end

		<link href="https://csdnimg.cn/release/phoenix/mdeditor/markdown_views-7f770a53f2.css" rel="stylesheet"></div><script>(function(){function setArticleH(btnReadmore,posi){var winH = $(window).height();var articleBox = $("div.article_content");var artH = articleBox.height();if(artH > winH*posi){articleBox.css({'height':winH*posi+'px','overflow':'hidden'})btnReadmore.click(function(){articleBox.removeAttr("style");$(this).parent().remove();})}else{btnReadmore.parent().remove();}}var btnReadmore = $("#btn-readmore");if(btnReadmore.length>0){if(currentUserName){setArticleH(btnReadmore,3);}else{setArticleH(btnReadmore,1.2);}}})()</script></article>

4. 准确率(Accuracy), 精确率(Precision), 召回率(Recall)和F1-Measure

1.准确率(Accuracy), 精确率(Precision), 召回率(Recall)和F1-Measure
机器学习(ML),自然语言处理(NLP),信息检索(IR)等领域,评估(Evaluation)是一个必要的 工作,而其评价指标往往有如下几点:准确率(Accuracy),精确率(Precision),召回率(Recall)和F1-Measure。(注： 相对来说，IR 的 ground truth 很多时候是一个 Ordered List, 而不是一个 Bool 类型的 Unordered Collection，在都找到的情况下，排在第三名还是第四名损失并不是很大，而排在第一名和第一百名，虽然都是“找到了”，但是意义是不一样的，因此 更多可能适用于 MAP 之类评估指标。)

本文将简单介绍其中几个概念。中文中这几个评价指标翻译各有不同，所以一般情况下推荐使用英文。

现在我先假定一个具体场景作为例子。

假如某个班级有男生80人,女生20人,共计100人.目标是找出所有女生.
现在某人挑选出50个人,其中20人是女生,另外还错误的把30个男生也当作女生挑选出来了.
作为评估者的你需要来评估(evaluation)下他的工作

首先我们可以计算准确率(accuracy),其定义是: 对于给定的测试数据集，分类器正确分类的样本数与总样本数之比。也就是损失函数是0-1损失时测试数据集上的准确率[1].

这样说听起来有点抽象，简单说就是，前面的场景中，实际情况是那个班级有男的和女的两类，某人(也就是定义中所说的分类器)他又把班级中的人分为男女两类。accuracy需要得到的是此君分正确的人占总人数的比例。很容易，我们可以得到:他把其中70(20女+50男)人判定正确了,而总人数是100人，所以它的accuracy就是70 %(70 / 100).

由准确率，我们的确可以在一些场合，从某种意义上得到一个分类器是否有效，但它并不总是能有效的评价一个分类器的工作。举个例子,google抓取了argcv 100个页面，而它索引中共有10,000,000个页面,随机抽一个页面，分类下,这是不是argcv的页面呢?如果以accuracy来判断我的工作，那我会把所有的页面都判断为"不是argcv的页面",因为我这样效率非常高(return false,一句话),而accuracy已经到了99.999%(9,999,900/10,000,000),完爆其它很多分类器辛辛苦苦算的值,而我这个算法显然不是需求期待的,那怎么解决呢?这就是precision,recall和f1-measure出场的时间了.

在说precision,recall和f1-measure之前,我们需要先需要定义TP,FN,FP,TN四种分类情况.
按照前面例子,我们需要从一个班级中的人中寻找所有女生,如果把这个任务当成一个分类器的话,那么女生就是我们需要的,而男生不是,所以我们称女生为"正类",而男生为"负类".

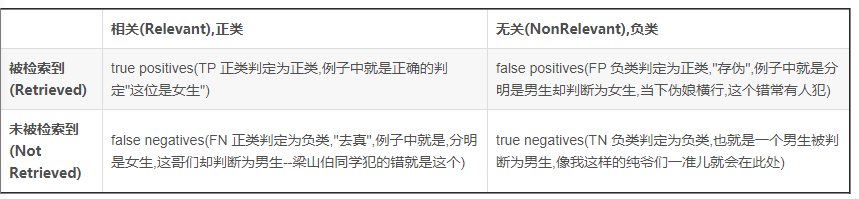
通过这张表,我们可以很容易得到这几个值:
TP=20
FP=30
FN=0
TN=50

精确率(precision)的公式是P = \frac{TP}{TP+FP},它计算的是所有"正确被检索的item(TP)"占所有"实际被检索到的(TP+FP)"的比例.

在例子中就是希望知道此君得到的所有人中,正确的人(也就是女生)占有的比例.所以其precision也就是40%(20女生/(20女生+30误判为女生的男生)).

召回率(recall)的公式是R = \frac{TP}{TP+FN},它计算的是所有"正确被检索的item(TP)"占所有"应该检索到的item(TP+FN)"的比例。

在例子中就是希望知道此君得到的女生占本班中所有女生的比例,所以其recall也就是100%(20女生/(20女生+ 0 误判为男生的女生))

F1值就是精确值和召回率的调和均值,也就是
\frac{2}{F_1} = \frac{1}{P} + \frac{1}{R}
调整下也就是
F_1 = \frac{2PR}{P+R} = \frac{2TP}{2TP + FP + FN}

例子中 F1-measure 也就是约为 57.143%(\frac{2 * 0.4 * 1}{0.4 + 1}).

需要说明的是,有人[2]列了这样个公式
F_a = \frac{(a^2 + 1 )PR}{a^2(P+R)}
将F-measure一般化.
F1-measure认为精确率和召回率的权重是一样的,但有些场景下,我们可能认为精确率会更加重要,调整参数a,使用Fa-measure可以帮助我们更好的evaluate结果.

准确率、召回率、F1
信息检索、分类、识别、翻译等领域两个最基本指标是召回率(Recall Rate)和准确率(Precision Rate)，召回率也叫查全率，准确率也叫查准率，概念公式:

召回率(Recall) = 系统检索到的相关文件 / 系统所有相关的文件总数
准确率(Precision) = 系统检索到的相关文件 / 系统所有检索到的文件总数

A： （搜到的也想要的）
B：检索到的，但是不相关的 （搜到的但没用的）
C：未检索到的，但却是相关的 （没搜到，然而实际上想要的）
D：未检索到的，也不相关的 （没搜到也没用的）

注意：准确率和召回率是互相影响的，理想情况下肯定是做到两者都高，但是一般情况下准确率高、召回率就低，召回率低、准确率高，当然如果两者都低，那是什么地方出问题了。一般情况，用不同的阀值，统计出一组不同阀值下的精确率和召回率，如下图：

如果是做搜索，那就是保证召回的情况下提升准确率；如果做疾病监测、反垃圾，则是保准确率的条件下，提升召回。所以，在两者都要求高的情况下，可以用F1来衡量。
F1 = * P * R / (P + R)

AP和mAP(mean Average Precision)
mAP是为解决P，R，F-measure的单点值局限性的。为了得到 一个能够反映全局性能的指标，可以看考察下图，其中两条曲线(方块点与圆点)分布对应了两个检索系统的准确率-召回率曲线

可以看出，虽然两个系统的性能曲线有所交叠但是以圆点标示的系统的性能在绝大多数情况下要远好于用方块标示的系统。

从中我们可以 发现一点，如果一个系统的性能较好，其曲线应当尽可能的向上突出。

更加具体的，曲线与坐标轴之间的面积应当越大。

最理想的系统， 其包含的面积应当是1，而所有系统的包含的面积都应当大于0。这就是用以评价信息检索系统的最常用性能指标，平均准确率mAP其规范的定义如下:(其中P，R分别为准确率与召回率)

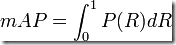
ROC和AUC
ROC和AUC是评价分类器的指标，上面第一个图的ABCD仍然使用，只是需要稍微变换。

回到ROC上来，ROC的全名叫做Receiver Operating Characteristic。

ROC关注两个指标

True Positive Rate ( TPR ) = TP / [ TP + FN] ，TPR代表能将正例分对的概率

False Positive Rate( FPR ) = FP / [ FP + TN] ，FPR代表将负例错分为正例的概率

在ROC 空间中，每个点的横坐标是FPR，纵坐标是TPR，这也就描绘了分类器在TP（真正的正例）和FP（错误的正例）间的trade-off。ROC的主要分析工具是一个画在ROC空间的曲线——ROC curve。我们知道，对于二值分类问题，实例的值往往是连续值，我们通过设定一个阈值，将实例分类到正类或者负类（比如大于阈值划分为正类）。因此我们可以变化阈值，根据不同的阈值进行分类，根据分类结果计算得到ROC空间中相应的点，连接这些点就形成ROC curve。ROC curve经过（0,0）（1,1），实际上(0, 0)和(1, 1)连线形成的ROC curve实际上代表的是一个随机分类器。一般情况下，这个曲线都应该处于(0, 0)和(1, 1)连线的上方。如图所示。

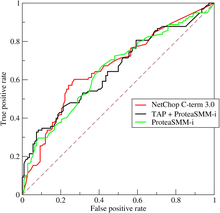
用ROC curve来表示分类器的performance很直观好用。可是，人们总是希望能有一个数值来标志分类器的好坏。

于是Area Under roc Curve(AUC)就出现了。顾名思义，AUC的值就是处于ROC curve下方的那部分面积的大小。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的Performance。

AUC计算工具：http://mark.goadrich.com/programs/AUC/

P/R和ROC是两个不同的评价指标和计算方式，一般情况下，检索用前者，分类、识别等用后者。
参考链接：http://www.vanjor.org/blog/2010/11/recall-precision/
http://bubblexc.com/y2011/148/
http://wenku.baidu.com/view/ef91f011cc7931b765ce15ec.html

：Recall，又称“查全率”——还是查全率好记，也更能体现其实质意义。
准确率

“召回率”与“准确率”虽然没有必然的关系（从上面公式中可以看到），在实际应用中，是相互制约的。要根据实际需求，找到一个平衡点。
当我们问检索系统某一件事的所有细节时（输入检索query查询词），Recall指：检索系统能“回忆”起那些事的多少细节，通俗来讲就是“回忆的能力”。“能回忆起来的细节数” 除以 “系统知道这件事的所有细节”，就是“记忆率”，也就是recall——召回率。简单的，也可以理解为查全率。

图像分割评价标准代码
main function （输入图像SEG 和 GT 分别为算法分割结果图像、分割金标准图像。对于多类分割的图像，需要先取出SEG和GT中对应的各类，然后使用下述函数单独计算该类。）

% test all segmentation metric functions  
SEG = imread('0.png');  
GT = imread('1.png');  % binarize  
SEG = im2bw(SEG, 0.1);  
GT = im2bw(GT, 0.1);  dr = Dice_Ratio(SEG, GT)  
hd = Hausdorff_Dist(SEG, GT)  
jaccard = Jaccard_Index(SEG, GT)  
apd = Avg_PerpenDist(SEG, GT)  
confm_index = ConformityCoefficient(SEG, GT)  
precision = Precision(SEG, GT)  
recall = Recall(SEG, GT)  

Dice_Ratio(即calDSI函数文件):

function dr = Dice_Ratio(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % dice ratio  dr = 2*double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(SEG(:))) + sum(uint8(GT(:))));  
end  

Hausdorff_Dist （得到hd 之后，还需要乘以像素的物理距离，才是真正的 Hausdorff 距离）（update: 对于三维体数据中该距离的计算，ITK方面给出的计算流程是：先将体数据匹配到同一物理空间，然后进行计算，这就要求两个体数据必须具备相同的物理参数。所以本代码不适用于三维体数据的计算。）:

function hd = Hausdorff_Dist(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % erode element  s = cat(3, [0 0 0 ; 0 1 0 ; 0 0 0], [0 1 0 ; 1 1 1 ; 0 1 0], [0 0 0 ; 0 1 0 ; 0 0 0]);  % generate boundary  Boundary_SEG = logical(SEG) & ~imerode(logical(SEG), s);  Boundary_GT = logical(GT) & ~imerode(logical(GT), s);  % distance to nearest boundary point  Dist_SEG = bwdist(Boundary_SEG, 'euclidean');  Dist_GT = bwdist(Boundary_GT, 'euclidean');  % distance to another boundary  min_S2G = sort(Dist_GT( Boundary_SEG(:) ), 'ascend');  min_G2S = sort(Dist_SEG( Boundary_GT(:) ), 'ascend');  % hausdorff distance  hd = max(min_S2G(end), min_G2S(end));  
end  

Jaccard_Index:

function jaccard = Jaccard_Index(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % jaccard index  jaccard = double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(SEG(:) | GT(:))));  
end  

Avg_PerpenDist （得到 apd 之后，还需要乘以像素的物理距离，才是真正的 apd 值）:

function apd = Avg_PerpenDist(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % erode element  s = cat(3, [0 0 0 ; 0 1 0 ; 0 0 0], [0 1 0 ; 1 1 1 ; 0 1 0], [0 0 0 ; 0 1 0 ; 0 0 0]);  % generate boundary  Boundary_SEG = logical(SEG) & ~imerode(logical(SEG), s);  Boundary_GT = logical(GT) & ~imerode(logical(GT), s);  % distance to nearest boundary point  Dist_GT = bwdist(Boundary_GT, 'euclidean');  % distance to another boundary  min_S2G = Dist_GT( Boundary_SEG(:) );  % average perpendicular distance from SEG to GT  apd = sum(min_S2G(:)) / length(min_S2G(:));  
end  

ConformityCoefficient:

function confm_index = ConformityCoefficient(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % dice ratio  dr = 2*double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(SEG(:))) + sum(uint8(GT(:))));  % conformity coefficient  confm_index = (3*dr - 2) / dr;  
end  

Precision:

function precision = Precision(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % precision  precision = double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(SEG(:))));  
end 

Recall:

function recall = Recall(SEG, GT)  % SEG, GT are the binary segmentation and ground truth areas, respectively.  % recall  recall = double(sum(uint8(SEG(:) & GT(:)))) / double(sum(uint8(GT(:))));  
end