光栅化2(抗锯齿)(Rasterization 2 - Antialiasing)
抗锯齿的内容包括:
- 采样理论(Sampling theory)
- 抗锯齿的实践应用(Antialiasing in practice)
接着上节
我们采样是在每个像素的中心进行采样,然后判断这个像素中心是否在三角形内,如果是三角形内就对其进行上色

最终得到的效果就是由多个像素均匀的正方形像素所组成的三角形:

emmmm,和我们想要的三角形不太一样,多了许多的棱角,不够平滑

在这个棱角很多的三角形中发生了一些采样错误,我们称其为锯齿。

锯齿在平常很常见,比如对一张图片放大,就可以明显看到锯齿,或者在游戏中,如果关闭了抗锯齿的选项,也能够看到很明显的锯齿

锯齿到底怎么来的,需要先从采样的理论开始说:
采样在图形学中广泛存在

光栅化 = 在2D的位置上进行采样

图片 = 对图像传感器进行采样

视频 = 在时间上进行采样
什么是视频呢,视频时将一系列图片连续的放出来从而达到一个连续的动画效果。人眼在观看视频时,就是对其中不同的时间上的图像进行采样,将这些采样的图像连接起来,最终得到一个动画的效果。比如一般动画片都是每秒24帧,就是说一秒内播放24张图片,然后人眼对这24张图片进行采样,得到动画的效果。每秒播放的图片越多,动画越流畅。

图形学中的采样错误(Sampling Artifacts in Computer Graphics)
采样错误有多种,如锯齿就是其中之一。

图像中的莫尔纹(Moiré Patterns in Imaging),也是一种采样错误。如下图所示,左边是原图,右边在采样时跳过了图像中的奇数行和列。

还有一种车轮效应,比如我们在看高速运转的车轮时,会发现车轮有时顺时针旋转,有时逆时针旋转,这也是一种采样错误
究竟为什么会出现采样错误?
信号变化的速度太快(主要指高频信号变化太快),而采样的速度太慢,最终结果就是会导致采样错误。
抗走样的主要思想:在采样之前进行模糊处理(Antialiasing idea:bluring before sampling)
如果不对其进行模糊处理,直接采样,就会出现下图的效果:

这样进行采样,就会发现:锯齿状的三角形像素值总为纯红或者纯白。单纯的两种颜色在边缘发生突变,就会导只锯齿十分的明显。
如果先对其进行模糊处理,然后再采样呢?

可以看到采样点增加了,并且在边缘处有一些颜色比较淡的点。也就是在光栅化的过程中,三角形的抗锯齿边缘的像素取了一个介于红色和白色之间的像素值,再进行染色时,边缘的像素点就会染色为中间值,边缘就能够获得一些更加平滑的效果,起到抗锯齿的作用。如下图所示:

下面左图为直接采样,右图为先模糊后采样的效果:

那么问题来了,如果先采样后模糊,会得到什么效果呢?

如左图所示,并不能实现抗锯齿的效果。那么问题就来了:
- 为什么采样不足会导致锯齿?
- 为什么先模糊后采样能够抗锯齿,而先采样后模糊不行?
要解释上面的愿意就要引入频域了
频域(Frequency Domain)
首先从最简单的正弦波和余弦波开始看:

用正弦和余弦有什么好处呢?

如果把正弦和余弦的系数f考虑进去,就可以得到频率不同的正弦波和余弦波,其中f就是频率。
傅里叶变换(Fourier Transform)
傅里叶变换就是说,一个函数f(x),能够分解成许多不同的正弦波或者余弦波的和。
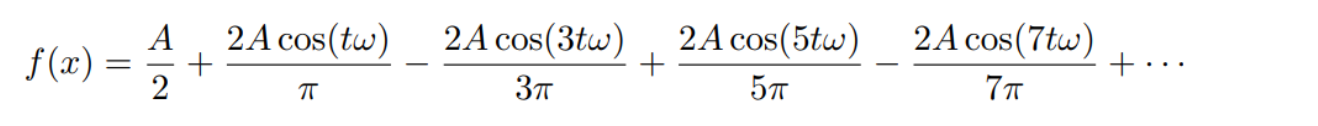
具体反应到函数图像上就是:

从第一个函数图像看,只有一个余弦波,将这个波加上一个数,让其整体向上位移,但是与目标函数f(x)相差很远
往下面看就可以发现,越来越多不同频率的余弦波叠加,最后就能够得到一个近似f(x)的函数图像。
**傅里叶变换的作用:**将信号从时域转换到频域。(时域并不是说就一定是时间的信息。图像并不带任何时间的信息,但我们认为空间上的信息也算是时域,时域只是一个单纯的名字。这里指把图像从图像的空间变换到频率的空间)

其逆变换能够从频域变换回时域。
之前曾经提到,因为采样速度跟不上信号变化的频率,所以导致采样出错。下面这个图就能解释:

垂直的虚线为采样点,绿色为函数图像,从上到下频率依次增高,黑点为在函数上采样的点,蓝色的虚线是将采样的点链接一起。
f1(x)中,采样的点的线连起来比较接近原来的图像,而下面随着频率的升高,连起来的蓝色的虚线无法再还原成原来的函数图像。所以就会导致采样出错。
要解决采样的错误,解决办法就是在采样之前进行模糊,既然说到模糊了,就不得不说一下滤波
滤波器 = 抛弃特定频率的内容(Filtering = Getting rid of certain frequency contents)
先看一个将图像转换到频域的例子:

左图为原图,右图为经过傅里叶变换得到图像的频谱,其中中间最亮的部分为低频率范围,而边上黑色的部分为高频率范围。
先看一下高通滤波器的效果:

高通滤波器消除了图像中的低频信息,然后在对频谱进行逆变换得到原图,最终得到的图像只有边缘的信息,为什么?因为某一点是边界点的话,那么该点的上下、或者左右的变化就会非常大,所以该点的信号变化就会非常大。所以高频信息代表着图像的边缘。
再看一下低通滤波器的效果:

低通滤波器消除了图像中的高频信息,最后得到的频谱逆变换为原图后,发现原图已经是一个模糊的效果。因为高频信息代表着图像的边界以及一些更为细节的信息,如果抹去高频信息,那么图像的细节就会消除,最后得到的就是模糊的图像。
中通滤波器:


两个为不同的中通滤波器的效果,下面的图通过的高频信息更多,图像的边界就更清楚一些,而上图通过的低频信息多,图像就更模糊一些。
滤波器 = 卷积 = 平均 (Filtering = Convolution = Averaging)
卷积的运算方法不做过多赘述,下面大概了解一下卷积定理:两个信号在时域上的卷积结果,就等价于,将两个信号转换到对应的频域,然后再用两个频谱相乘得到的结果。
卷积的运算方式:
- 直接用卷积核在时域上进行卷积运算
-
- 先将图像通过傅里叶变换转换到频域
- 在将卷积核通过傅里叶变换转换到频域,并且将两个频谱相乘
- 将最后得到的结果通过逆傅里叶变换转换到时域

上图就表示了卷积运算的两种方式。看一下在频域的变换,卷积核变换到频域后只保留了低频信息,然后将两个频谱相乘,最后得到的也只有低频信息,再对其进行逆傅里叶变换,最终就得到了一个模糊的图像。(低频信息图像时模糊图像,前面提到过)
卷积核 / 滤波器(Convolution Kernel / Box Filter)

这个卷积核就是求图像上某一点周围像素的平均值,然后将最后得到的结果作为中心点的像素。 前面的系数 1/9 是一个很特殊的数,把1/9乘到卷积核里,最后得到的卷积核内部九个数的和为1。如果不×1/9,那么周围的所有像素相加就会越加越亮,最后可能会导致全白的结果。也就是说,如果卷积核的和 = 1,就能够保持和原来图像相同的亮度,大于1图像就会变亮,小于1图像边暗。

一个滤波器有一定的大小,如上左图为一个滤波器在时域中的大小,右图为滤波器反应到频域中的状态。那么应该思考,如果滤波器在时域上的大小变大或者变小,频域会发生什么变化?
举个例子,使用3*3的滤波器能够达到一个使图像模糊的效果,如果用5 * 5, 7 * 7 ,甚至更大的滤波器,会得到什么效果呢?随着滤波器大小的增大,图像会变得越来越模糊,因为取平均值的范围越大,那么这个范围内的像素的区别就会越小,图像也就会越模糊;与之相反,如果用一个1 *1 的滤波器呢?那就相当于没有进行滤波,图像也就不会变模糊。
综合上面的信息,可以得到,滤波器越大,其图像越模糊,那么就说明能够通过的频率就越低,频谱上对应的频率的范围也就会变小。

上图就是滤波器变大,而对应的频率变得更低。
采样 = 重复 频率的内容 (Sampling = Repeating Frequency Contents)

上图a是一个连续函数的图像,b是a对应的频域的图像。我们要对函数a进行采样,如何进行采样呢?采样就是对函数进行离散化的过程,只保留函数上某些特定位置的函数值,其余不要。这就相当于 一个函数× 另一个函数。 反应到上图就是 a × c (c是冲激函数), 得到的结果e就是对a采样的结果,可以看到这个采样能够还原函数a的图像。
我们说,时域上的乘积 = 频域上的卷积,也就是说我在时域上对 a×c的操作,在频域上要把b和d进行卷积。b卷积d的结果就是f,就可以发现在时域上对一个连续函数进行采样,而在频域上,则是对该连续函数的频谱进行了一个复制粘贴的操作。所以说采样是什么,采样就是重复一个原始信号的频谱。也就是说在时域上进行采样 等价于 在频域上进行周期延拓。
在有了这样的理解之后,就可以探讨为什么会产生走样的现象
走样 = 频率内容混合 (Aliasing = Mixed Frequency Contents)

上面两幅图反映了不同采样频率下,最后得到的频域的频谱图。
采样不同的间隔,会影响频谱会以另外一种间隔移动。在第一行中,进行密集的采样时,频谱的移动范围间隔较大,能够保证各个频段分隔不会相互影响。而在下面的第二行中,当采样的频率不够时,频谱的移动范围就会变小,最终导致频谱混叠,这种情况下就发生了走样。
为什么时域和频域的间隔是互为反比的关系呢?我们上面已经讲到,采样相当于连续函数乘一个冲激函数,而冲激函数的间隔就是在时域上采样的间隔,因为冲激函数在频域里的间隔是时域里的倒数,所以时域越宽,频域越窄。
既然已经了解到为何会出现走样,那么接下来就应该来看一下,如何抗走样。
反走样(Antiliasing)
如何减少走样?
Option 1 : 提高采样率
- 提高显示器分辨率。如果用一个640*480的显示器,光栅化一个三角形,就能够明显发现锯齿很严重,但是如果使用1920 * 1080的显示器就能够明显改善这种情况
- 但是这种情况需要依赖于高分辨率的显示器,若是显示器分辨率不能改变时,这种方法就不行了
Option2 : 反走样
- 先把一个信号的高频信息抹除
- 然后再采样

如上图,在采样之前,先用滤波器(虚线框)抹除掉高频率的信息,然后再对图像进行采样。可以看到,如果不用滤波器进行滤波,那么就会像之前一样,在高频段的部分会导致频谱的叠加,然后发生走样。用滤波器进行滤波之后,就不会在发生频谱的叠加,也就减少了走样。
上面就是先用模糊再采样能够反走样的原理。
然后再回到我们的做法当中,先模糊 再采样 = 抗走样

在实际中,用什么样的滤波器进行一个模糊的操作?使用一个一定大小的低通滤波器对三角形进行卷积,就可以得到模糊的效果。
计算平均像素值实现抗走样(Antialiasing by Computing Average Pixel Value)
对于任何一个像素,被三角形覆盖的情况只有三种:1.完全被覆盖 2. 完全不被覆盖 3.部分被覆盖

对于任何一个被覆盖的像素,我们要计算这个像素的平均值就是看被覆盖的面积占整个像素多少比例,比如图1,三角形覆盖了1/8,未覆盖7/8,那么这个点的平均像素就是 1/8的黑色+7/8的白色作为最终的像素值。就是说把像素内部的值给平均一下,这就是所作的卷积操作。
MSAA(Antialiasing By Supersampling)
我将其翻译为通过多重采样反走样。
因为按照上面的那种求每个像素中的区域百分比十分困难,所以就有了MSAA这种反走样的方法,其思想也是如上面的那种方法,但是取的是一个近似的求区域像素平均值的方法。
什么是多重采样?
在之前采样时,都是对一个像素的像素中心进行一次采样。那么超采样就是对一个像素进行多次采样,如下图所示:

将一个像素划分为 4*4个小像素,每一个小像素都有一个像素中心,然后可以对这个小像素进行采样,判断这些小像素在不在三角形内,然后将最后的结果平均起来,就能够求的三角形对一个像素的区域的近似的覆盖。比如:

可以看到一个三角形覆盖了若干个像素,每个像素都挺大的。
假如说我把一个像素分为四个小像素,在像素内部多加一些采样点

然后每个点都可以判断是否在三角形内,如果四个点都在三角形内就是100%覆盖,如果只有三个点在三角形内,则三角形对这个像素就是75%覆盖。于是就可以得出每个像素的覆盖结果

通过这么一种方法,可以做到一个抗锯齿的效果。
有一点要注意:MSAA通过更多的样本,来近似的进行反走样的第一步,模糊,这个过程。模糊完了之后就相当于每一个像素内部都已经知道了三角形的覆盖率,求了平均之后是什么,就会得到上图的结果。到了这一步,就相当于模糊做完了,就相当于用卷积核对图像进行了一次卷积得到了模糊的效果。然后再采样,这时采样就会十分简单,以为每个格子的颜色都是平均的,采样完也就会得到上图的结果。
MSAA解决的是对信号进行模糊的操作,而采样的这一部操作实际上是隐含在了模糊的过程中。
MSAA的过程:
- 将每个像素划分为多个小像素
- 判断每个小像素的中心是否在三角形内部,从而得到三角形在该像素的覆盖率
- 得到覆盖率之后对这个像素的像素值进行平均,得到上图的结果
- 然后采样
MSAA并不是通过提高采样率而完成的,对更多的点进行采样只是为了得到三角形在一个像素上的覆盖比率而已。
MSAA的缺陷
MSAA提高了计算的量,将一个像素划分为多个区域,就要对每个区域进行多次计算,最后就提高了计算的成本。
其他反走样方式
- FXAA (Fast Approximate AA)
- TAA (Temporal AA)