• 本文介绍如何用 DQN 及它的两个改进 Double DQN & Dueling DQN 解二维滚球问题，这个环境可以看做 gym Maze2d 的简单版本
• 参考：《动手学强化学习》
• 完整代码下载：5_[Gym Custom] RollingBall (DQN and Double DQN and Dueling DQN)

---

1. 二维滚球环境

1.1 环境介绍

• 想象二维平面上的一个滚球，对它施加水平和竖直方向的两个力，滚球就会在加速度作用下运动起来，当球碰到平面边缘时会发生完全弹性碰撞，我们希望滚球在力的作用下尽快到达目标位置
  

• 此环境的状态空间为

  维度	意义	取值范围
  0	滚球 x 轴坐标	$[0,\text{width}]$
  1	滚球 y 轴坐标	$[0,\text{height}]$
  2	滚球 x 轴速度	$[-5.0,5.0]$
  3	滚球 y 轴速度	$[-5.0,5.0]$

  动作空间为

  维度	意义	取值范围
  0	施加在滚球 x 轴方向的力	$[-1.0,1.0]$
  1	施加在滚球 y 轴方向的力	$[-1.0,1.0]$

  奖励函数为

  事件	奖励值
  到达目标位置	$300.0$
  发生反弹	$-10.0$
  移动一步	$-2.0$

1.2 代码实现

• 通过 gym 的环境自定义方法实现以上二维滚球环境，具体的环境自定义方法可以参考：RL gym 环境（2）—— 自定义环境

  值得一提的是，借助 chatgpt 可以大幅提高这类工具代码的编写效率，以下代码有 80% 都是 chatgpt 自动生成的

• 代码实现

  import gym
  from gym import spaces
  import numpy as np
  import pygame
  import timeclass RollingBall(gym.Env):metadata = {"render_modes": ["human", "rgb_array"],     # 支持的渲染模式，'rgb_array' 仅用于手动交互"render_fps": 500,}                         # 渲染帧率def __init__(self, render_mode="human", width=10, height=10, show_epi=False):self.max_speed = 5.0self.width = widthself.height = heightself.show_epi = show_epiself.action_space = spaces.Box(low=-1.0, high=1.0, shape=(2,), dtype=np.float64)self.observation_space = spaces.Box(low=np.array([0.0, 0.0, -self.max_speed, -self.max_speed]), high=np.array([width, height, self.max_speed, self.max_speed]),dtype=np.float64)self.velocity = np.zeros(2, dtype=np.float64)self.mass = 0.005self.time_step = 0.01# 奖励参数self.rewards = {'step':-2.0, 'bounce':-10.0, 'goal':300.0}# 起止位置self.target_position = np.array([self.width*0.8, self.height*0.8], dtype=np.float32)self.start_position = np.array([width*0.2, height*0.2], dtype=np.float64)self.position = self.start_position.copy()# 渲染相关self.render_width = 300self.render_height = 300self.scale = self.render_width / self.widthself.window = None# 用于存储滚球经过的轨迹self.trajectory = []# 渲染模式支持 'human' 或 'rgb_array'assert render_mode is None or render_mode in self.metadata["render_modes"]self.render_mode = render_mode# 渲染模式为 render_mode == 'human' 时用于渲染窗口的组件self.window = Noneself.clock = Nonedef _get_obs(self):return np.hstack((self.position, self.velocity))def _get_info(self):return {}def step(self, action):# 计算加速度#force = action * self.massacceleration = action / self.mass# 更新速度和位置self.velocity += acceleration * self.time_stepself.velocity = np.clip(self.velocity, -self.max_speed, self.max_speed)self.position += self.velocity * self.time_step# 计算奖励reward = self.rewards['step']# 处理边界碰撞reward = self._handle_boundary_collision(reward)# 检查是否到达目标状态terminated, truncated = False, Falseif self._is_goal_reached():terminated = Truereward += self.rewards['goal']  # 到达目标状态的奖励obs, info = self._get_obs(), self._get_info()self.trajectory.append(obs.copy())  # 记录滚球轨迹return obs, reward, terminated, truncated, infodef reset(self, seed=None, options=None):# 通过 super 初始化并使用基类的 self.np_random 随机数生成器super().reset(seed=seed)# 重置滚球位置、速度、轨迹self.position = self.start_position.copy()self.velocity = np.zeros(2, dtype=np.float64)self.trajectory = []return self._get_obs(), self._get_info()def _handle_boundary_collision(self, reward):if self.position[0] <= 0:self.position[0] = 0self.velocity[0] *= -1reward += self.rewards['bounce']elif self.position[0] >= self.width:self.position[0] = self.widthself.velocity[0] *= -1reward += self.rewards['bounce']if self.position[1] <= 0:self.position[1] = 0self.velocity[1] *= -1reward += self.rewards['bounce']elif self.position[1] >= self.height:self.position[1] = self.heightself.velocity[1] *= -1reward += self.rewards['bounce']return rewarddef _is_goal_reached(self):# 检查是否到达目标状态（例如，滚球到达特定位置）# 这里只做了一个简单的判断，可根据需要进行修改distance = np.linalg.norm(self.position - self.target_position)return distance < 1.0  # 判断距离是否小于阈值def render(self):if self.render_mode not in ["rgb_array", "human"]:raise Falseself._render_frame()def _render_frame(self):canvas = pygame.Surface((self.render_width, self.render_height))canvas.fill((255, 255, 255))    # 背景白色if self.window is None and self.render_mode == "human":pygame.init()pygame.display.init()self.window = pygame.display.set_mode((self.render_width, self.render_height))if self.clock is None and self.render_mode == "human":self.clock = pygame.time.Clock()# 绘制目标位置target_position_render = self._convert_to_render_coordinate(self.target_position)pygame.draw.circle(canvas, (100, 100, 200), target_position_render, 20)# 绘制球的位置ball_position_render = self._convert_to_render_coordinate(self.position)pygame.draw.circle(canvas, (0, 0, 255), ball_position_render, 10)# 绘制滚球轨迹if self.show_epi:for i in range(len(self.trajectory)-1):position_from = self.trajectory[i]position_to = self.trajectory[i+1]position_from = self._convert_to_render_coordinate(position_from)position_to = self._convert_to_render_coordinate(position_to)color = int(230 * (i / len(self.trajectory)))  # 根据轨迹时间确定颜色深浅pygame.draw.lines(canvas, (color, color, color), False, [position_from, position_to], width=3)# 'human' 渲染模式下会弹出窗口if self.render_mode == "human":# The following line copies our drawings from `canvas` to the visible windowself.window.blit(canvas, canvas.get_rect())pygame.event.pump()pygame.display.update()# We need to ensure that human-rendering occurs at the predefined framerate.# The following line will automatically add a delay to keep the framerate stable.self.clock.tick(self.metadata["render_fps"])# 'rgb_array' 渲染模式下画面会转换为像素 ndarray 形式返回，适用于用 CNN 进行状态观测的情况，为避免影响观测不要渲染价值颜色和策略else:return np.transpose(np.array(pygame.surfarray.pixels3d(canvas)), axes=(1, 0, 2))def close(self):if self.window is not None:pygame.quit()def _convert_to_render_coordinate(self, position):return int(position[0] * self.scale), int(self.render_height - position[1] * self.scale)
  

• 由于 DQN 类方法都只能用于离散动作空间，我们进一步编写动作包装类，将原生的二维连续动作离散化并拉平为一维离散动作空间

  class DiscreteActionWrapper(gym.ActionWrapper):''' 将 RollingBall 环境的二维连续动作空间离散化为二维离散动作空间 '''def __init__(self, env, bins):super().__init__(env)bin_width = 2.0 / binsself.action_space = spaces.MultiDiscrete([bins, bins]) self.action_mapping = {i : -1+(i+0.5)*bin_width for i in range(bins)}def action(self, action):# 用向量化函数实现高效 action 映射vectorized_func = np.vectorize(lambda x: self.action_mapping[x])    result = vectorized_func(action)action = np.array(result)return actionclass FlattenActionSpaceWrapper(gym.ActionWrapper):''' 将多维离散动作空间拉平成一维动作空间 '''def __init__(self, env):super(FlattenActionSpaceWrapper, self).__init__(env)new_size = 1for dim in self.env.action_space.nvec:new_size *= dimself.action_space = spaces.Discrete(new_size)def action(self, action):orig_action = []for dim in reversed(self.env.action_space.nvec):orig_action.append(action % dim)action //= dimorig_action.reverse()return np.array(orig_action)
  

• 随机策略测试代码

  import os
  import sys
  base_path = os.path.abspath(os.path.join(os.path.dirname(__file__), '..'))
  sys.path.append(base_path)import numpy as np
  import time
  from gym.utils.env_checker import check_env
  from environment.Env_RollingBall import RollingBall, DiscreteActionWrapper, FlattenActionSpaceWrapper
  from gym.wrappers import TimeLimit env = RollingBall(render_mode='human', width=5, height=5, show_epi=True)    
  env = FlattenActionSpaceWrapper(DiscreteActionWrapper(env, 5))
  env = TimeLimit(env, 100)
  check_env(env.unwrapped)    # 检查环境是否符合 gym 规范
  env.action_space.seed(10)
  observation, _ = env.reset(seed=10)# 测试环境
  for i in range(100):while True:action = env.action_space.sample()#action = 19state, reward, terminated, truncated, _ = env.step(action)if terminated or truncated:env.reset()breaktime.sleep(0.01)env.render()# 关闭环境渲染
  env.close()
  

2. 使用 DQN 系列方法求解

2.1 DQN

2.1.1 算法原理

• DQN 方法的出发点是将 Q-Learning 扩展到连续、高维状态空间中，这些情况下无法构造 Q-Learning 中的 Q 表。DQN
  使用函数近似方法来拟合无限大的 Q 表，该网络输入一个状态，输出各个动作的 Q 价值
  
  注意到网络的输出个数为动作空间尺寸，因此 DQN 方法仅适用于离散动作空间的环境。在训练使用 $\omega$ 参数化的 DQN 网络 $Q_{\omega }$ 时，我们通过优化关于 TD error 的 mse loss，来让价值估计靠近 TD target
  $${\omega }^{\ast }=\arg \underset{\omega }{\min }\frac{1}{2N}\sum _{i=1}^N{\left[\left(r_i+\gamma \underset{a^{\prime }}{\max }{Q}_{\omega }\left(s_i^{\prime },a^{\prime }\right)\right)-Q_{\omega }\left(s_i,a_i\right)\right]}^2$$ 其中 $N$ 为 batch size
• 如果 online 地使当前交互得到的 transition 样本去更新网络参数，会导致 训练不稳定、数据相关性强 和 数据利用率低 等问题。这里的核心矛盾在于 DQN 的训练方式本质是监督学习，而 on-policy RL 框架违背了监督学习基本的 i.i.d 原则。为了解决这个问题，DQN 引入了 经验重放 方法，维护一个 transition 缓冲区，将每次从环境中采样得到的 transition 四元组数据 $(s,a,r,s^{\prime })$ 存储到回放缓冲区中，训练 $Q$ 网络的时候再从回放缓冲区中随机采样若干数据来进行训练
  
  这样可以增强训练数据的 i.i.d 性质，并且增加样本利用率
• 使用经验重放机制仍然不足以稳定训练。注意到 DQN 训练的本质还是 Q-Learning 的 TD boostrap 迭代方法，分析上面的损失函数，我们是在使用由 DQN 生成的优化目标 TD target 来优化 DQN 网络。这就导致优化目标随着训练进行不断变化，违背了监督学习的 i.i.d 原则，导致训练不稳定。为了解决这一问题，进一步引入目标网络，它的结构、输入输出等和 DQN 完全一致，每隔一段时间，就把其网络参数 ${\omega }^{-}$ 更新为 DQN 网络参数 $\omega$，其唯一的作用就是给出 TD target $$r_i+\gamma \underset{a^{\prime }}{\max }{Q}_{{\omega }^{-}}\left(s_i^{\prime },a^{\prime }\right)$$ 在两次参数更新之间目标网络被冻结，这样就能给出平稳的优化目标，让训练更稳定。除此以外，目标网络部分打破了 DQN 自身的 Bootstrapping 操作，一定程度上缓解了 Q 价值高估的问题。
• DQN 论文的详细解读见：论文理解【RL经典】 —— 【DQN】Human-level control through deep reinforcement learning

2.1.2 代码实现

• 经验重放缓冲区（replay buffer）

  class ReplayBuffer:''' 经验回放池 '''def __init__(self, capacity):self.buffer = collections.deque(maxlen=capacity)        # 先进先出队列def add(self, state, action, reward, next_state, done):  self.buffer.append((state, action, reward, next_state, done))def sample(self, batch_size):  transitions = random.sample(self.buffer, batch_size)state, action, reward, next_state, done = zip(*transitions)return np.array(state), np.array(action), reward, np.array(next_state), donedef size(self): return len(self.buffer)
  

• DQN 网络

  class Q_Net(torch.nn.Module):''' Q 网络是一个两层 MLP, 用于 DQN 和 Double DQN '''def __init__(self, input_dim, hidden_dim, output_dim):super().__init__()self.fc1 = torch.nn.Linear(input_dim, hidden_dim)self.fc2 = torch.nn.Linear(hidden_dim, output_dim)def forward(self, x):x = F.relu(self.fc1(x)) return self.fc2(x)
  

• DQN agent

  class DQN(torch.nn.Module):''' DQN算法 '''def __init__(self, state_dim, hidden_dim, action_dim, action_range, lr, gamma, epsilon, target_update, device, seed=None):super().__init__()self.action_dim = action_dimself.state_dim = state_dimself.hidden_dim = hidden_dimself.action_range = action_range        # action 取值范围self.gamma = gamma                      # 折扣因子self.epsilon = epsilon                  # epsilon-greedyself.target_update = target_update      # 目标网络更新频率self.count = 0                          # Q_Net 更新计数self.rng = np.random.RandomState(seed)  # agent 使用的随机数生成器self.device = device                # Q 网络self.q_net = Q_Net(state_dim, hidden_dim, action_range).to(device)  # 目标网络self.target_q_net = Q_Net(state_dim, hidden_dim, action_range).to(device)# 使用Adam优化器self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=lr)def max_q_value_of_given_state(self, state):state = torch.tensor(state, dtype=torch.float).to(self.device)return self.q_net(state).max().item()def take_action(self, state):  ''' 按照 epsilon-greedy 策略采样动作 '''if self.rng.random() < self.epsilon:action = self.rng.randint(self.action_range)else:state = torch.tensor(state, dtype=torch.float).to(self.device)action = self.q_net(state).argmax().item()return actiondef update(self, transition_dict):states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)                             # (bsz, state_dim)next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)                   # (bsz, state_dim)actions = torch.tensor(transition_dict['actions'], dtype=torch.int64).view(-1, 1).to(self.device)               # (bsz, act_dim)rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device).squeeze()     # (bsz, )dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device).squeeze()         # (bsz, )q_values = self.q_net(states).gather(dim=1, index=actions).squeeze()                # (bsz, )max_next_q_values = self.target_q_net(next_states).max(axis=1)[0]                   # (bsz, )q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)                  # (bsz, )dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))  self.optimizer.zero_grad()                                                         dqn_loss.backward() self.optimizer.step()if self.count % self.target_update == 0:# 按一定间隔更新 target 网络参数self.target_q_net.load_state_dict(self.q_net.state_dict())  self.count += 1
  

• 训练并绘制性能曲线

  if __name__ == "__main__":def moving_average(a, window_size):''' 生成序列 a 的滑动平均序列 '''cumulative_sum = np.cumsum(np.insert(a, 0, 0)) middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_sizer = np.arange(1, window_size-1, 2)begin = np.cumsum(a[:window_size-1])[::2] / rend = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]return np.concatenate((begin, middle, end))def set_seed(env, seed=42):''' 设置随机种子 '''env.action_space.seed(seed)env.reset(seed=seed)random.seed(seed)np.random.seed(seed)torch.manual_seed(seed)state_dim = 4                               # 环境观测维度action_dim = 1                              # 环境动作维度action_bins = 10                            # 动作离散 bins 数量action_range = action_bins * action_bins    # 环境动作空间大小hidden_dim = 32lr = 1e-3num_episodes = 1000gamma = 0.99epsilon_start = 0.01epsilon_end = 0.001target_update = 1000buffer_size = 10000minimal_size = 5000batch_size = 128device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")# build environmentenv = RollingBall(width=5, height=5, show_epi=True)    env = FlattenActionSpaceWrapper(DiscreteActionWrapper(env, bins=10))env = TimeLimit(env, 100)check_env(env.unwrapped)            # 检查环境是否符合 gym 规范set_seed(env, seed=42)              # build agentreplay_buffer = ReplayBuffer(buffer_size)agent = DQN(state_dim, hidden_dim, action_dim, action_range, lr, gamma, epsilon_start, target_update, device)# 随机动作来填充 replay bufferstate, _ = env.reset()while replay_buffer.size() <= minimal_size:action = env.action_space.sample()next_state, reward, terminated, truncated, _ = env.step(action)replay_buffer.add(state, action, reward, next_state, done=terminated or truncated)if terminated or truncated:env.render()state, _ = env.reset()#print(replay_buffer.size())# 开始训练return_list = []max_q_value_list = []max_q_value = 0for i in range(20):with tqdm(total=int(num_episodes / 20), desc='Iteration %d' % i) as pbar:for i_episode in range(int(num_episodes / 20)):episode_return = 0state, _ = env.reset()while True:# 保存经过状态的最大Q值max_q_value = agent.max_q_value_of_given_state(state) * 0.005 + max_q_value * 0.995 # 平滑处理max_q_value_list.append(max_q_value)                                    # 选择动作移动一步action = agent.take_action(state)next_state, reward, terminated, truncated, _ = env.step(action)# 更新replay_bufferreplay_buffer.add(state, action, reward, next_state, done=terminated or truncated)# 当buffer数据的数量超过一定值后,才进行Q网络训练assert replay_buffer.size() > minimal_sizeb_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)transition_dict = {'states': b_s,'actions': b_a,'next_states': b_ns,'rewards': b_r,'dones': b_d}agent.update(transition_dict)state = next_stateepisode_return += rewardif terminated or truncated:env.render()break#env.render()return_list.append(episode_return)if (i_episode + 1) % 10 == 0:pbar.set_postfix({'episode':'%d' % (num_episodes / 10 * i + i_episode + 1),'return':'%.3f' % np.mean(return_list[-10:])})pbar.update(1)#env.render()agent.epsilon += (epsilon_end - epsilon_start) / 10# show policy performencemv_return_list = moving_average(return_list, 29)episodes_list = list(range(len(return_list)))plt.figure(figsize=(12,8))plt.plot(episodes_list, return_list, label='raw', alpha=0.5)plt.plot(episodes_list, mv_return_list, label='moving ave')plt.xlabel('Episodes')plt.ylabel('Returns')plt.title(f'{agent._get_name()} on RollingBall')plt.legend()plt.savefig(f'./result/{agent._get_name()}.png')plt.show()# show Max Q value during trainingframes_list = list(range(len(max_q_value_list)))plt.plot(frames_list, max_q_value_list)plt.axhline(max(max_q_value_list), c='orange', ls='--')plt.xlabel('Frames')plt.ylabel('Max Q_value')plt.title(f'{agent._get_name()} on RollingBall')plt.savefig(f'./result/{agent._get_name()}_MaxQ.png')plt.show()
  

2.1.3 性能

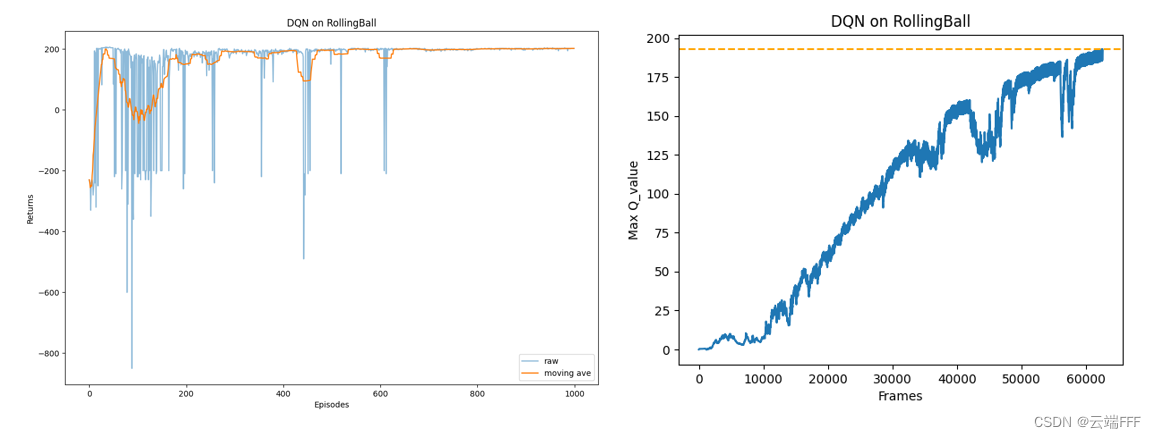
2.2 Double DQN

2.2.1 算法原理

• Bellman Optimal Equation 中有最大化 $\max$ 操作，这会导致价值函数的高估，而且高估会被 bootstrap 机制不断加剧 最终我们得到的是真实 $Q^{\ast }$ 的有偏估计。其实高估本身没什么，但关键是高估是不均匀的，如果某个 $(s,a)$ 被迭代计算更多，那么由于 bootstrap 机制其价值也被高估更多，显然 replay buffer 中的 $(s,a)$ 分布是不均匀的，很可能某个次优动作就变成最优动作了，这会导致 agent 性能下降

• 我们可以对 $Q$ 值的过高估计做简化的定量分析。假设在状态 $s$ 下所有动作的期望回报均无差异，即 $Q^{\ast }(s,a)=V^{\ast }(s)$（此设置是为了定量分析所简化的情形，实际上不同动作的期望回报通常会存在差异）；假设神经网络估算误差 $Q_{{\omega }^{-}}(s,a)-Q^{\ast }(s,a)$ 服从 $[-1,1]$ 之间的均匀独立同分布；假设动作空间大小为 $m$。那么，对于任意状态，有 $$\mathbb{E}\left[\underset{a}{\max }{Q}_{{\omega }^{-}}(s,a)-\underset{a^{\prime }}{\max }{Q}_{\ast }\left(s,a^{\prime }\right)\right]=\frac{m-1}{m+1}$$ 即动作空间越大时，$Q$ 值过高估计越严重

  

• $Q$ 价值过估计问题在表格型的 Q-learning 中也存在，一个解决方案是把选择动作和计算价值分开处理，这种方法称为 Double Q-learning ，详见强化学习笔记（6）—— 无模型（model-free）control问题 5.4 节。Double DQN 方法模仿 Double Q-learning 的思路处理了 DQN 的价值高估问题，它做的改动其实非常小，观察 TD target 公式
  $$y=r_i+\gamma \underset{a^{\prime }}{\max }{Q}_{{\omega }^{-}}\left(s_i^{\prime },a^{\prime }\right)$$ 它可以看作选择最优动作 $a^{\ast }$ 和计算 TD target $y$ 两步

  1. 原始 DQN 中，两步都用目标网络完成，即
     $$\begin{gathered} a^{\ast }=\underset{a^{\prime }}{\mathrm{argmax}}{Q}_{{\omega }^{-}}\left(s_i^{\prime },a^{\prime }\right) \\ y=r+\gamma Q_{{\omega }^{-}}\left(s_i^{\prime },a^{\ast }\right) \end{gathered}$$
  2. Double DQN 中，第一步用 DQN 完成，第二步用目标网络完成，即
     $$\begin{gathered} a^{\ast }=\underset{a^{\prime }}{\mathrm{argmax}}{Q}_{\omega }\left(s_i^{\prime },a^{\prime }\right) \\ y=r+\gamma Q_{{\omega }^{-}}\left(s_i^{\prime },a^{\ast }\right) \end{gathered}$$

  显然有（左边来自 Double DQN，右边来自 DQN）
  $$Q_{{\omega }^{-}}\left(s_i^{\prime },\underset{a^{\prime }}{\mathrm{argmax}}{Q}_{\omega }\left(s_i^{\prime },a^{\prime }\right)\right)\le \underset{a^{\prime }}{\max }{Q}_{{\omega }^{-}}(s_i^{\prime },a^{\prime })$$ 因此 Double DQN 得到的估计值比 DQN 更小一些。总的来看，DDQN 不但缓解了最大化导致的偏差，还和 DQN 一样部分缓解了 Bootstrapping 导致的偏差，因此其价值估计更准确

2.2.2 代码实现

• 继承原始 DQN 类，修改其中的 update 方法即可

  class Double_DQN(DQN):''' Double DQN算法 '''        def update(self, transition_dict):states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)                             # (bsz, state_dim)next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)                   # (bsz, state_dim)actions = torch.tensor(transition_dict['actions'], dtype=torch.int64).view(-1, 1).to(self.device)               # (bsz, act_dim)rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device).squeeze()     # (bsz, )dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device).squeeze()         # (bsz, )q_values = self.q_net(states).gather(dim=1, index=actions).squeeze()                # (bsz, )max_action = self.q_net(next_states).max(axis=1)[1]                                 # (bsz, )max_next_q_values = self.target_q_net(next_states).gather(dim=1, index=max_action.unsqueeze(1)).squeeze()             q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)                  # (bsz, )dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))  self.optimizer.zero_grad()                                                         dqn_loss.backward() self.optimizer.step()if self.count % self.target_update == 0:# 按一定间隔更新 target 网络参数self.target_q_net.load_state_dict(self.q_net.state_dict())  self.count += 1
  

• 其余代码都可以维持不变

2.2.3 性能

• 注意到 Double DQN 的最大 $Q$ 价值估计相比普通 DQN 减少很多，说明值过高估计的问题得到了很大缓解

2.3 Dueling DQN

2.3.1 算法原理

• RL 中 $Q(s,a)$ 价值可以拆分为 $V(s)$ 价值和动作优势 $A(s,a)$ 之和，即
  $$Q(s,a)=V(s)+A(s,a)$$ 根据价值函数定义 $V(s)={\mathbb{E}}_a\left[Q(s,a)\right]$，在同一个状态下所有动作的优势值之和 ${\sum }_{a}A(s,a)=0$
• DQN 和 Double DQN 都是直接对 $Q$ 函数进行建模，而 Dueling DQN 对 $A$ 和 $V$ 分别建模，通过组合二者来计算 $Q$ 函数。这样做的好处在于：某些情境下智能体只会关注状态的价值，而并不关心不同动作导致的差异，此时将二者分开建模能够使智能体更好地处理与动作关联较小的状态
  
  如图所示的驾驶车辆游戏中，agent 注意力集中的部位被显示为橙色，当智能体前面没有车时，车辆自身动作并没有太大差异，此时智能体更关注状态（道路尽头位置）的价值，而当智能体前面有车时（智能体需要超车），智能体开始关注不同动作优势值的差异。
• 为了同时拟合 $V(s)$ 和 $A(s,a)$，将原始的 $Q(s,a)$ 改成一个共享隐藏层的双头 mlp，这可以理解为二者共享输入的状态特征，最后通过不同的线性组合参数组合得到 $A$ 和 $V$，公式表示如下
  $$Q_{\eta ,\alpha ,\beta }(s,a)=V_{\eta ,\alpha }(s)+A_{\eta ,\beta }(s,a)$$ 这里有一个对于值和值建模不唯一性的问题。例如，对于同样的 $Q$ 值，如果将 $V$ 值加上任意大小的常数 $C$，再将所有 $A$ 值减去 $C$，则得到的 $Q$ 值依然不变，这就导致了训练的不稳定性。为了解决这一问题，Dueling DQN 强制最优动作的优势函数的实际输出为 0，即
  $$Q_{\eta ,\alpha ,\beta }(s,a)=V_{\eta ,\alpha }(s)+A_{\eta ,\beta }(s,a)-\underset{a^{\prime }}{\max }{A}_{\eta ,\beta }\left(s,a^{\prime }\right)$$ 此时 $V(s)={\max }_{a}Q(s,a)$ 可以确保值建模的唯一性。在实现过程中，我们还可以用平均代替最大化操作，即：
  $$Q_{\eta ,\alpha ,\beta }(s,a)=V_{\eta ,\alpha }(s)+A_{\eta ,\beta }(s,a)-\frac{1}{|\mathcal{A}|}\sum _{a^{\prime }}{A}_{\eta ,\beta }\left(s,a^{\prime }\right)$$ 此时 $V(s)=\frac{1}{|\mathcal{A}|}{\sum }_{a^{\prime }}Q\left(s,a^{\prime }\right)$，虽然它不再满足贝尔曼最优方程，但实际应用时更加稳定
• Dueling DQN 能更高效学习状态价值函数。每一次更新时，$V$ 函数都会被更新，这也会影响到其他动作的 $Q$ 值。而传统的 DQN 只会更新某个动作的 $Q$ 值，其他动作的值就不会更新。由 Dueling DQN 的原理可知，随着动作空间的增大，Dueling DQN 相比于 DQN 的优势更为明显

2.3.2 代码实现

• 实现同时拟合 $V$ 和 $A$ 的双头网络

  class VA_Net(torch.nn.Module):''' VA 网络是一个两层双头 MLP, 仅用于 Dueling DQN '''def __init__(self, input_dim, hidden_dim, output_dim):super(VA_Net, self).__init__()self.fc1 = torch.nn.Linear(input_dim, hidden_dim)   # 共享网络部分self.fc_A = torch.nn.Linear(hidden_dim, output_dim)self.fc_V = torch.nn.Linear(hidden_dim, 1)def forward(self, x):A = self.fc_A(F.relu(self.fc1(x)))V = self.fc_V(F.relu(self.fc1(x)))Q = V + A - A.mean().item()                         # Q值由V值和A值计算得到return Q
  ``
  

• 继承原始 DQN 类，在初始化时重新将 q_net 和 target_q_net 重新指向 VA_Net 对象，并新建优化器

  class Dueling_DQN(DQN):''' Dueling DQN 算法 '''            def __init__(self, state_dim, hidden_dim, action_dim, action_range, lr, gamma, epsilon, target_update, device, seed=None):super().__init__(state_dim, hidden_dim, action_dim, action_range, lr, gamma, epsilon, target_update, device, seed)# Q 网络self.q_net = VA_Net(state_dim, hidden_dim, action_range).to(device)  # 目标网络self.target_q_net = VA_Net(state_dim, hidden_dim, action_range).to(device)# 使用Adam优化器self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=lr)
  

• 其余代码都可以维持不变

2.3.3 性能

3. 总结

• 本文讲解了 DQN 算法及其两个容易实现的变式 —— Double DQN 和 Dueling DQN
  1. DQN 的主要思想是用一个神经网络来拟合最优 $Q$ 函数，利用 Q-learning 的思想，通过优化 TD error 的 MSE 损失进行参数更新。为了保证训练的稳定性和高效性，DQN 算法引入了经验回放和目标网络两大模块
  2. Double DQN 将 TD target 的构造分成最优动作选取和提取价值两个部分，第一步用 DQN 完成，第二步用目标网络完成，缓解了 DQN 中对值的过高估计问题
  3. Dueling DQN 将对 $Q$ 函数的建模拆分成对 $V$ 和 $A$ 两部分进行建模，使智能体更好地处理与动作关联较小的状态，更高效学习状态价值函数。当动作空间很大时相对 DQN 有更大优势