均匀”的本质------贝特朗悖论的思考

摘要 贝特朗悖论是概率论中的著名悖论。文章对古典概型中的无差别原则以及引起争议的贝特朗悖论做出了简要解释和介绍，并通过线性条件修正对悖论的经典计算方法进行驳斥，最后肯定了悖论在数学发展历程中的重要意义。
关键词 贝特朗悖论无差别原则概率论公理化线性无差别条件古典概型

无差别原则

古典概率论的基础是伯努利（Jakob Bernoulli）和拉普拉斯（Pierre Simon Laplace）提出的“不充分理由原则”（The Principle of Insufficient Reason）。伯努利曾提出，“如果因为无知，使得我们没有办法判断哪一个结果会比另外一个结果更容易出现，那么应该给予它们相同的概率”。在不充分理由原则的基础上，皮埃尔-西蒙·拉普拉斯（Pierre-Simon Laplace）确立了古典概率的定义，即未知的概率都是等概率。逻辑学家凯恩斯（John Maynard Keynes）将这条原则固定下来并加以更名、完善。“无差别原则主张，对于主体进行预测是，如果没有已知的理由选取其中一种方案而不选取其他的备选方案，相对于这些知识每个备选方案的主张都应该具有相同的概率。因此，如果没有积极的理由来作为分配不平等的理由，那么每个论证都必须分配相等的概率。”这种认识也在十九世纪统一了数学界，并被广泛使用与发展。
对于古典概型而言，逻辑解释使用了无差别原则来作为确定初始概率的基本原则。然而由于无差别原则的主观性，其逻辑本身是有漏洞的，容易导致逻辑悖论。如果不能为无差别原则导致的逻辑悖论给出相应解释与合理的解决，那么会是对逻辑概率的毁灭。

贝特朗悖论的解读

1888年，法国数学家贝特朗（Joseph Louis Bertrand）在他的著作《概率的计算》（《Calcul des probabilités》）中构造了这样一个悖论：“在一个圆内任意选一条弦，这条弦的弦长长于这个圆的内接等边三角形的边长的概率是多少？”接着，贝特朗给出了三种不同的算法，并得到了1/2、1/3、1/4三个完全不同的答案。下面我们就对贝特朗悖论的三种算法进行介绍与阐述。
第一种算法：圆内的任意一条弦都一定与圆有两个交点，又由于圆的对称性，我们不妨先确定弦上一个点的位置，如图为点A。过该点做圆切线DE，那么圆上任意一点就可以与点A相连进而形成相应弦。我们将这条弦与DE的夹角称为 θ ，那么很显然，当θ∈(60°，120°) 时，这条弦的长度是大于三角形的边长的。我们没有理由说明θ是在区间[0°，180° ]中的某个值而不是其他值，所以根据无差别原则，θ在这个区间上是均匀分布的。因此我们可以得到，
P=((120°-60°))⁄(180°)=1⁄3
第二种算法：根据几何学的知识，我们可以先过一个顶点做这个圆的一条直径AD，刚好可以平分这个三角形。那么，在直径上任取一个点，可以做出平行于三角形边BC的弦。如果要使得我们做出的弦长大于三角形的边长，那么很显然，这些弦在下半圆内应该要处于BCB’C’内，即三角形边与直径之间。而直径AD在这部分中的长度OQ=R/2，根据对称性，在上半圆中符合要求弦长对应的区段长度也应该是R/2。同样根据无差别原则，我们可以认为弦中点M在直径AD上是均匀分布的，因此符合要求的区域应该是：
P=((2×R/2))⁄2R=1⁄2
第三种算法：我们现在考虑弦中点的位置，在内接三角形中再画一个三角形的内接圆，分别于三角形的三条边再相交。这个内接圆和大圆是同心圆，且小圆的半径是大圆半径的一半。如果弦的中点在小圆内部，则无论这条弦是怎样的旋转角度，它的长度都比三角形的边长腰长。同样根据无差别原则，弦中点的位置是均匀分布的，那么概率就应该用面积进行计算。这种情况下：
P=((π×(R/2)^2 ))⁄((π×R^2 ) )=1⁄4
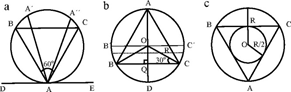
在这里插入图片描述

图为三种经典解法
令人难以接受的是，这三种答案在自身的推理步骤与相应结论上都是完全正确、令人信服与接受的，悖谬之处就在于这些推演以及他们的结果相互之间是不相容的。出于数学上的依据，贝特朗认为这样的演算有无穷多，但明显，一个带有无穷多结论的二律背反不能被压缩成一个论证。贝特朗对自己的悖论解答持有相当的怀疑态度：“在这三个答案中，真正的答案是哪一个？这三个答案都不是错误的，但也没有一个是确切的，而是这个问题提出的不合适。”
在此之后，包括杰恩斯（Edwin T.Jaynes）、泰勒（Dr. Charles E.Tyler）、陈小平、加德纳（Martin Gardner）在内的多位数学家通过实验试图对悖论进行验证与解读，但不同实验得到的结果也不尽相同，不同认知之间的摩擦碰撞不断发生，至今也始终没有确切的结论。

新思路的出现------线性无差条件

自悖论出现以来，除了上述的三种经典解答之外，也有诸多学者对该问题进行了不少研究与探讨。下介绍两种新的思路，并通过这两种思路对之前的三种方案进行反思与论证。
李文明对此问题做出了另一种解法，他从长度的方向出发分析，对问题给出了解答。贝特朗悖论的基本问题可以转化为：“圆内任取一条弦，其长度大于√3 R的概率是多少？”若圆的半径为R，则圆内弦长的取值必定在(0,2R] ┤之间。再对现场运用无差别原则可以得到:
P=((2-√3))⁄2
这种计算方式仅仅是考虑了弦长度的绝对值，将问题粗略地转化为一维进行运算。然而这种直接降为的方式虽易于理解但并没有强有力的理论支撑，且可以广泛利用到无数种其他模型，如把圆变成椭圆、正方形、长方形等，全部都可以等价计算。但很明显，这样的计算方式难以令人信服。
陈晓平在研究无差别原则的过程中，对酒水悖论和贝特朗悖论均有所探察，并对线性无差别条件做出了解释和修正。陈在吉利斯（Donald Gillies）理论的基础上提出了无差别条件，即对于某一复合函数，当且仅当该复合分布函数本身是均匀分布，且内部函数为一次函数时，内部函数才可以认为也是均匀分布。举个更为直观的例子，当横坐标上的动点在区间上匀速运动时，它投射到任意一条斜线上的点自然也是匀速移动；而若该动点的投射线为曲线，则曲线上的动点自然不是匀速运动。简言之，如果我们认定某一变量为均匀分布的，则对于与该变量相关的另一变量，其均匀性取决于自身是否为线性条件。
按照陈的观点，我们可以对第一种答案（即关于角度的概率问题）与第三种答案（关于面积的概率问题）进行相应反驳：对于第一种解释，我们考虑的是弦的长度，夹角θ显然是均匀分布的，但是弦长度ρ=2R cos⁡(π-θ/2)，二者之间的关系显然不是线性关系，因此可以认为在角度旋转变化的过程中，对应的弦长度是不均匀的；同样第三种答案中，目标函数为面积分布，应该与半径的平方呈线性关系，因此利用面积计算也并非“均匀分布”。笔者认为这种思路相对而言较为完善与妥当。

悖论以后

贝特朗悖论的出现使得人们对什么是概率的疑惑放大到了极致。人们明白必须要解决这个问题，解决问题的方法就是给出概率的严密的定义，再在此基础上推演概率的理论体系，即将概率论公理化。1900年，Hilbert在数学家大会上提出了23个20世纪应该解决的数学问题，建立概率的公理化体系就在列其中。希尔伯特建议用数学的公理化方法推演出全部物理，首先是概率和力学。1993年，前苏联数学家柯尔莫哥洛夫建立了概率论的公理化体系。可以说，悖论的出现对公理化体系的建立起到了不可低估的作用；而公理化体系的建立，沟通了概率论和其他数学分支的联系。
在数学的发展史上，每一次悖论的出现，都是数学理论体系漏洞的暴露；每一次悖论的出现，都是人们重新思考与完善数学基础的机会。数学史上三次大的数学危机的出现都与悖论密不可分，同样都使得数学大厦不断坚固，并在此过程中愈加光辉灿烂。