这里写目录标题
- C语言底层逻辑剖析函数篇(其三),函数递归与迭代超详解,递归经典例题斐波那契数列,汉诺塔问题,青蛙跳台阶
- 开篇语
- 函数递归
- 递归的两个必要条件
- 递归案例1
- 递归案例2
- 递归和迭代
- 递归经典例题——斐波那契数列
- 汉诺塔问题和青蛙跳台阶问题
C语言底层逻辑剖析函数篇(其三),函数递归与迭代超详解,递归经典例题斐波那契数列,汉诺塔问题,青蛙跳台阶
开篇语
对于本节内容相对来说也是比较难的,但是函数递归却是C语言中一个非常重要的知识点,是一定一定要掌握的,如果第一遍没有看懂也没有关系,递归这个东西就是需要多看多画图去理解,下面我会介绍画图的方法,帮助大家来理解,当然我也会尽量写的详细去解释清楚,所以这期内容可是花费了不少精力,如果觉得还不错就点赞收藏一下吧!
函数递归
函数递归在C语言中是极其重要并且难以理解的知识点,所以我们才会单独拿出一期内容来单独学习,大家集中精力,开始发车了。
由于递归的定义并不太好描述并且比较抽象,我们来看一下,
程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。
一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略,只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
乍一看其实是极为抽象的,不要着急我们要结合例子来理解,我们还需要先记住,递归的核心思想其实就是大事化小,将一个复杂问题不断简化为一个与其相似但是较小的问题,那么接下来我们先来看一个史上最简单但是是错误的递归,死递归;先要知道递归是什么东西,
代码如下:
#include<stdio.h>
int main()
{printf("hehe\n");main();return 0;
}
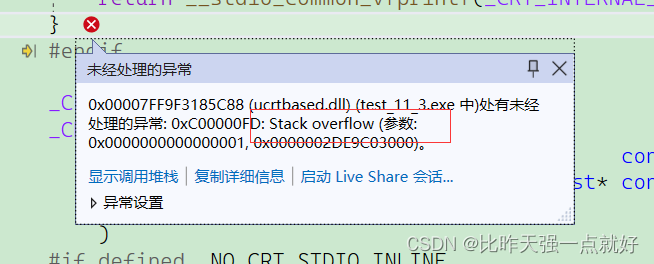
我们来分析一下这段代码,我在main函数里调用了main函数,这就是递归最最基本的使用思想。但是这段代码是一个典型的死递归,为什么叫死递归呢,因为他是个错误的递归,如果你拿这段代码去编译器上去运行,你会发现它死循环的打印hehe,但是打印到一定数量后这个程序就崩溃了,如果你去调试还会弹出一个错误警告:
stack
overflow,意思是栈溢出了。栈是什么呢?这不是我们这一期要重点学习的内容,我们下一期会专门来解释函数栈帧问题,详细解释变量是怎么定义和销毁的,以及函数是怎样传参和工作的过程,现在你只需要留下一个概念栈区就是计算机一块存储空间,而每次调用函数都会向内存申请创建一块空间,而这个死递归不断的去调用函数,就会把栈区耗干,这就是栈溢出了。
递归的两个必要条件
在我们使用递归的过程中一般会两个非常重要的地方,这两个地方也是我们要好好去斟酌的地方,
1.存在限制条件,当满足这个限制条件的时候,递归便不再继续。
2.每次递归调用之后越来越接近这个限制条件。
什么意思呢,我们先来看一个递归的案例:
递归案例1
题目:接受一个整型值(无符号),按照顺序打印它的每一位。
例如:输入1234
输出:1 2 3 4;
我们需要先来整理一下思路

要取到每一个数字的话我们只有一条路可走,就是不断地%10,得到它的余数,但是如果直接%10先打印出的一定是4,而我们的目的要先打印1,这里我们可以考虑用递归,如图,我们要打印1234的每一位,我们可以化解成打印123的每一位和4,而打印123的每一位又可以分解,最终函数实现的代码如下:
#include<stdio.h>
void Print(int num)
{if ((num / 10) != 0){Print(num/10);}printf("%d ",num%10);}int main()
{int num = 0;scanf("%d",&num);//假设我要使用Print函数来帮我打印出1234Print(num);return 0;
}
看到这里我相信你是很懵逼的,不要着急,既然说了要讲清楚,接下来我们通过一个图来解释一下
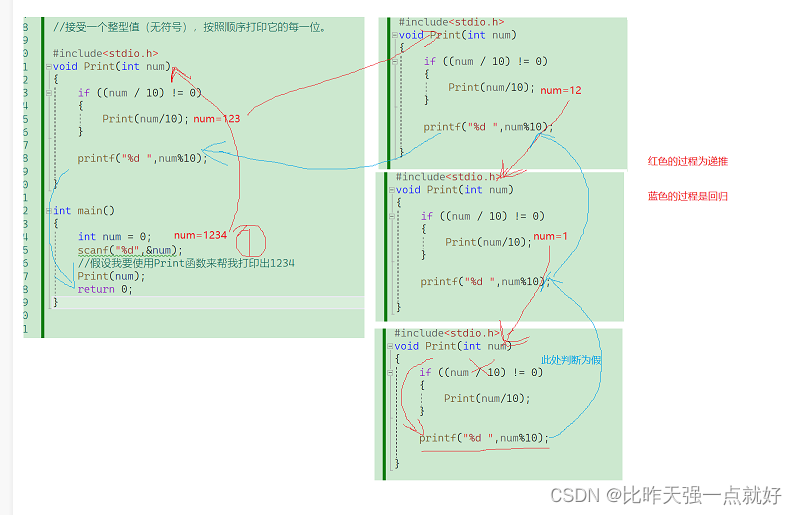
我们先走的是红色的过程不断函数里面套函数,然后最后条件不满足的时候就开始回归,所以条件此处一定要好好斟酌,否则你的递归很容易就是个死递归,就会造成程序崩溃,我们再来看这个代码,仅仅几行代码就完成了大量的重复性的工作,但是一个很明显的缺点就是难想出来,但是也不要慌张,慢慢来。关于递归真正的存在的问题下面我们会讨论。
递归案例2
题目:编写函数不允许创建临时变量,求字符串的长度
求字符串长度我们已经学过一个函数strlen,那么这个题目的意思不就是让我们自己编写一个strlen出来吗?
假设我们先不考虑题目条件,允许创建临时变量,我们应该怎么样写,我们先理清一下思路,我们只要创建一个临时变量,将数组里每一个元素依次与‘\0’来比较,如果不是就让变量加一,当为‘\0’时意味着字符串结束了,这时候返回这个值即可,那么我们来看代码如何写呢?
#include<stdio.h>int my_strlen(char* pa)
{int count = 0; while ((*pa != '\0')){//pa++;意味着向后跳一个字符;//类似的,如果是整形++,意味着向后跳一个整形,大小4个字节;pa++;count++;}return count;
}int main()
{char arr[] = "abcdef";//数组名本身是字符串第一个元素的地址int ret=my_strlen(arr);printf("%d\n",ret);return 0;
}
好好分析一下这个代码,我们要以这个思路为铺垫,虽然我们创建了临时变量,不符合题目要求,如果要考虑题目条件,下面我们用递归的方式来解决,

这是我们分析的基本思路,有了这个思路代码就很好写了。
#include<stdio.h>
int my_strlen(char* pa)
{if (*pa != '\0')return 1 + my_strlen(pa + 1);elsereturn 0;
}int main()
{char arr[] = "abcdef";int ret = my_strlen(arr);printf("%d\n",ret);return 0;
}
这就是我们题目要求的代码,如果你还是看不懂,没有关系,我们依旧是通过画图的方式来理解;
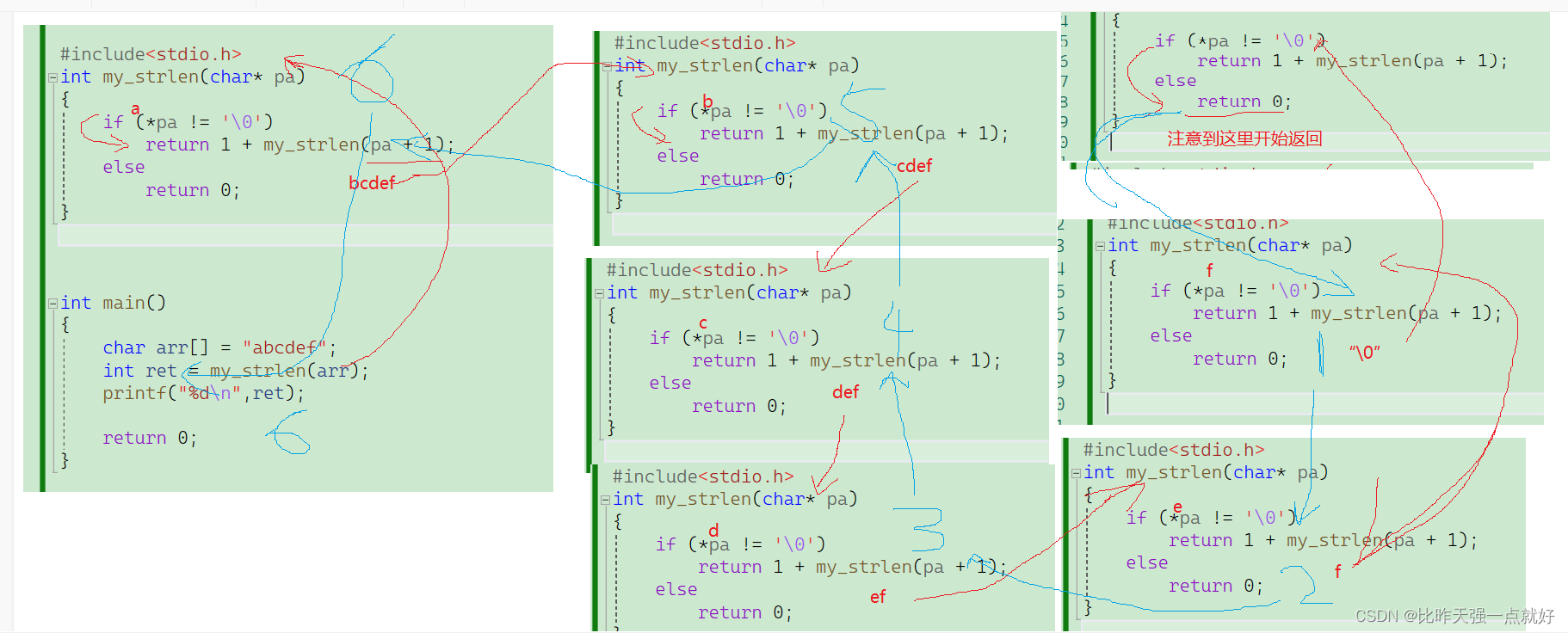
其中红色的线是递推的过程,蓝色的是回归的过程。关于递归这个画图已经是最好的理解方式了,一定要多画图理解,当你慢慢见的多了就掌握了,当然递归也是必须掌握的,当到后面学习数据结构的时候,你会发现用递归可能几行代码就解决了,但是用迭代的方式可能得几十行代码,但是也不要着急,我们以后慢慢理解。
递归和迭代
这里先来做一个小练习,
题目:求n的阶乘,我们要求用两种方法,一种是迭代(非递归),你可以看成循环就是一种迭代;另一种就是我们刚学的递归。
我们先来看第一种,学到现在我们看到这个题目应该思路立马就出来了,从1一直乘到n,写一个循环即可。
#include<stdio.h>
int mul(int n)
{int i = 0;int fac = 1;for (i = 1; i <= n; i++){fac *= i;}return fac;
}int main()
{int n = 0;scanf("%d",&n);int ret=mul(n);printf("%d\n",ret);return 0;
}
这是我们的第一种循环的写法,接下来我们看递归怎么写;
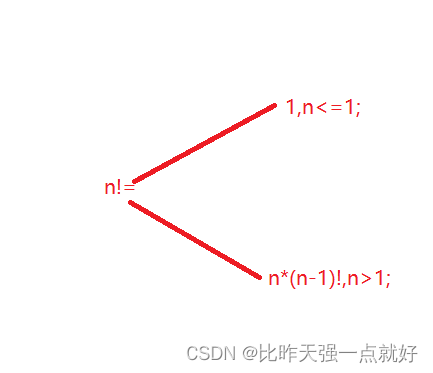
当我们有了这个公式,递归就非常好写了,我们来看代码:
#include<stdio.h>
int mul(int n)
{if (n <= 1)return 1;elsereturn n * mul(n-1);}int main()
{int n = 0;scanf("%d",&n);int ret = mul(n);printf("%d\n",ret);return 0;
}
推荐大家用上面画图的方式去好好理解一下。相信到这里你会对递归有一个深刻的理解。
这里我们使用了两种方式来解决这个问题,第一种是通过循环的方式,第二种是通过递归的方式,其实循环就是一种迭代,迭代的意思就是通过一次又一次的重复的方式去解决。迭代可以简单理解为循环。
递归经典例题——斐波那契数列
接下来就是我们的重头戏了,斐波那契数列问题,请一定一定要集中精力,下面我们会对递归和迭代的优缺点进行比较,这点是一定要注意的。
题目:求第n个斐波那契数。(不考虑溢出)
我们首先要知道什么是斐波那契数列,斐波那契数列就是1,1,2,3,5,8,13,21,34,55…我们找一下规律,其实就是前两个数相加得到第三个数。
我们还是要先分析一下思路:

有了这个思路我们的代码也是很简单了,我们先来看代码;
#include<stdio.h>int Fib(n)
{if (n <= 2)return 1;elsereturn Fib(n - 1) + Fib(n - 2);}int main()
{int n = 0;scanf("%d",&n);int ret=Fib(n);printf("%d\n",ret);return 0;
}
这个代码通过递归的方式很简单就写出来了,但是这段代码用递归的方式它真的是最好的解决办法吗?如果你去试一下求50的阶乘,你会发现你的电脑一直在运行,很长时间都算不出来,电脑是不会偷懒的,它是真的一直在运算。那么为什么会出现这种状况呢
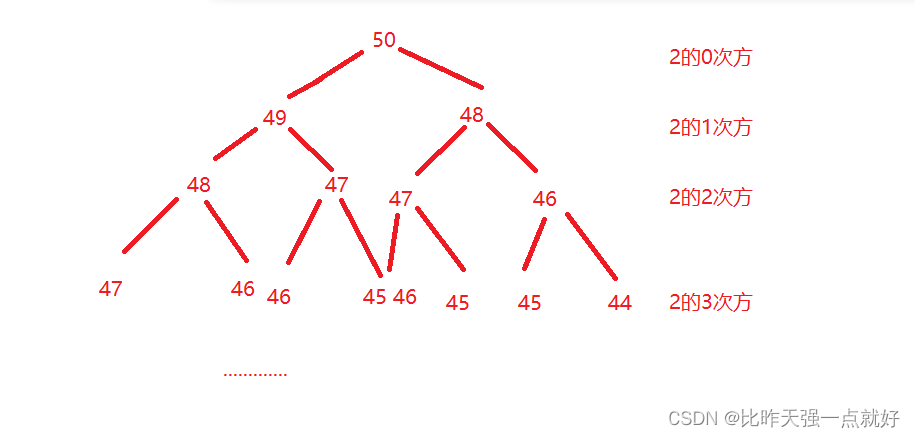
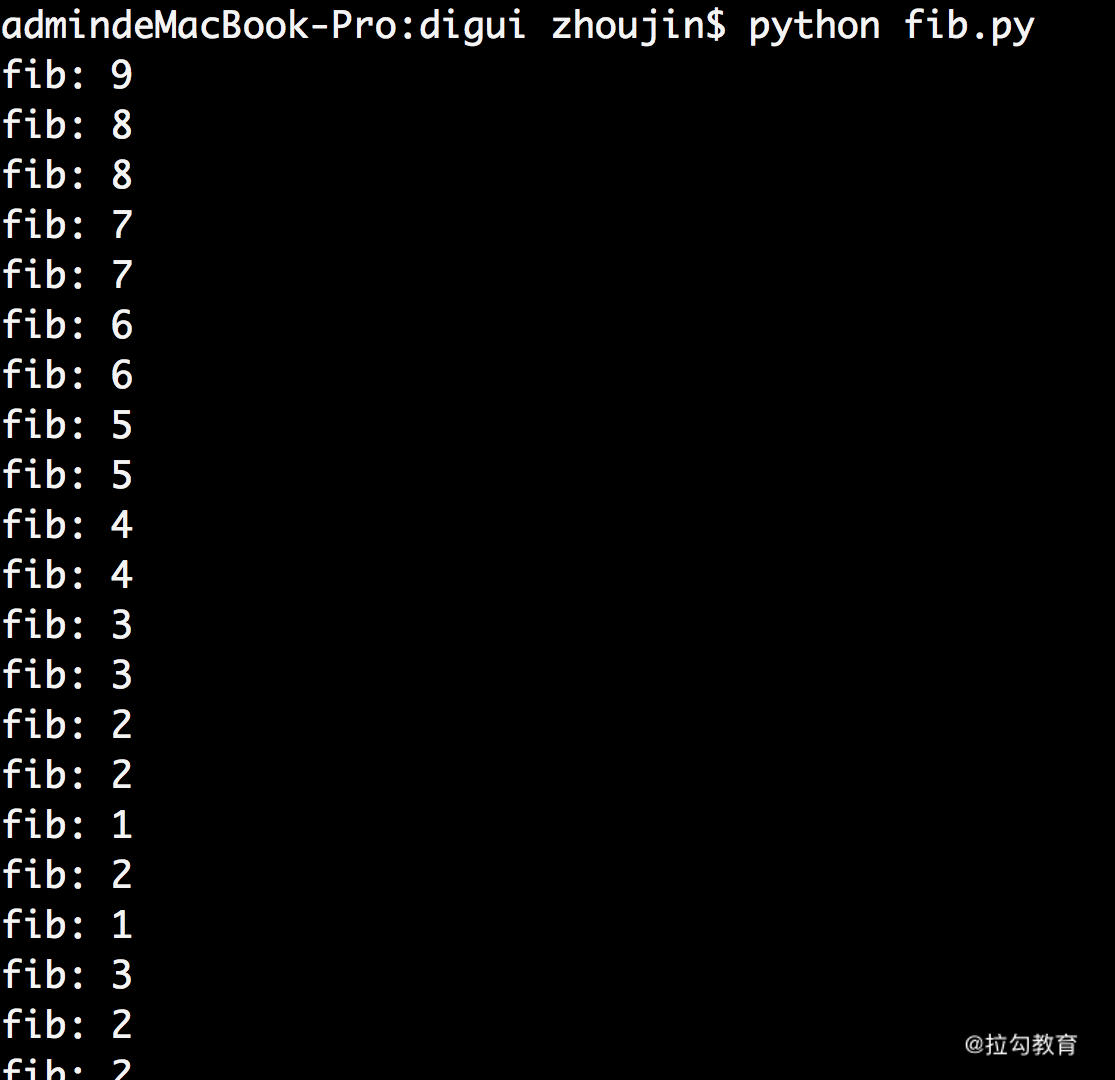
我们看一下它的运行思路,你会发现计算量是成指数式的爆炸式增长,当我们计算第50个斐波那契数的时候就是2的50次方,这多少有点难为电脑了,我们还会发现里面是有大量的重复计算,一个数字会被重复很多次我们可以在代码中来看一下:
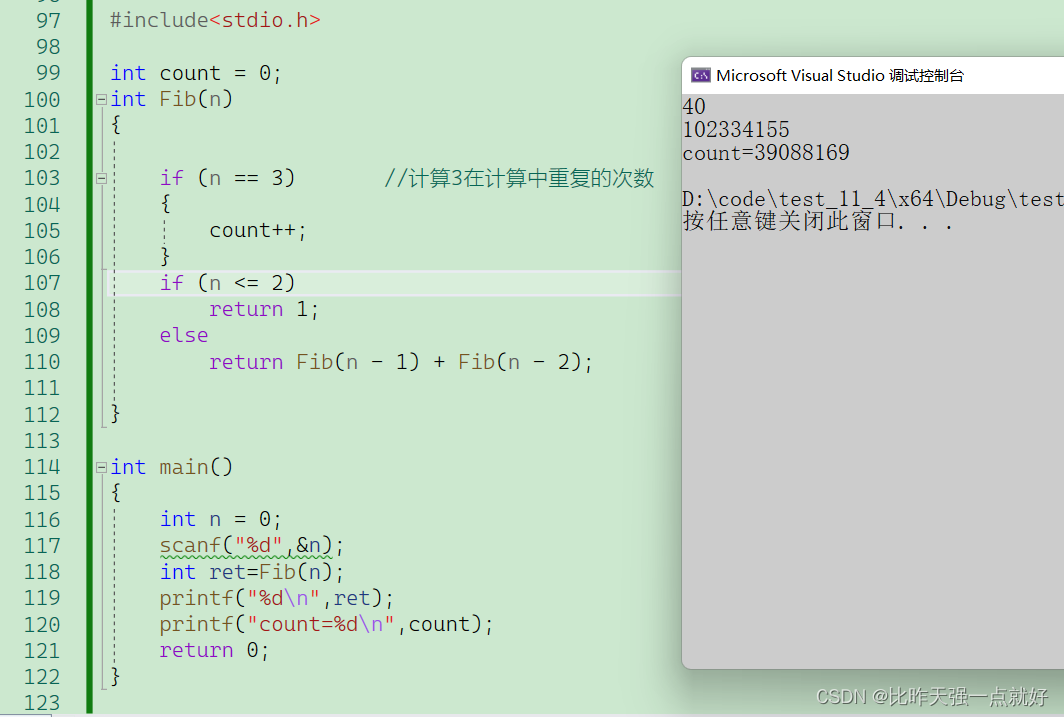
当我们计算40个斐波那契数的时候,仅仅是第3个这个数字就重复计算了3900多万次,可以发现这其实问题是非常大的。所以这时候用递归的方式可能就不太合适了。
我们就要考虑迭代的方式,那么我们怎么来解决呢?

所以我们代码的思路就有了,代码如下:
#include<stdio.h>
int Fib(n)
{int a = 1;int b = 1;int c = 1;while (n>2){c = a + b;a = b;b = c;n--;}return c;
}int main()
{int n = 0;scanf("%d",&n);int ret=Fib(n);printf("%d\n",ret);return 0;
}
接下来我们再来看一下我们求阶乘的代码,如果你要求一万的阶乘,递归和迭代的方式,分别去测试你会发现两个不同的结果:
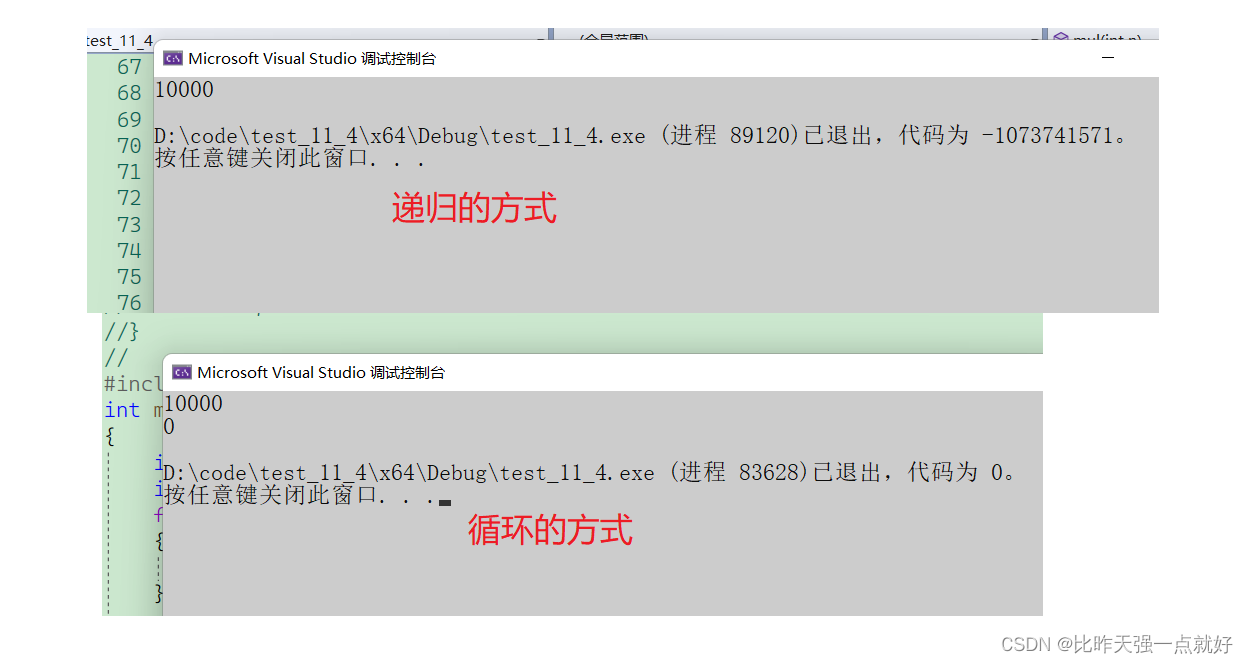
我们知道10000的阶乘肯定是放不下的,可以看到,如果是递归的方式,程序直接就崩了,但是迭代的方式虽然算出来结果是错的,但是至少不至于程序崩了。
这时候再回过头来对比递归和迭代,他们的优缺点其实很难说,迭代写起来比较麻烦,递归写起来简单却容易出问题,所以没有绝对的好坏,如果有的话,另一个就没有存在的必要了。
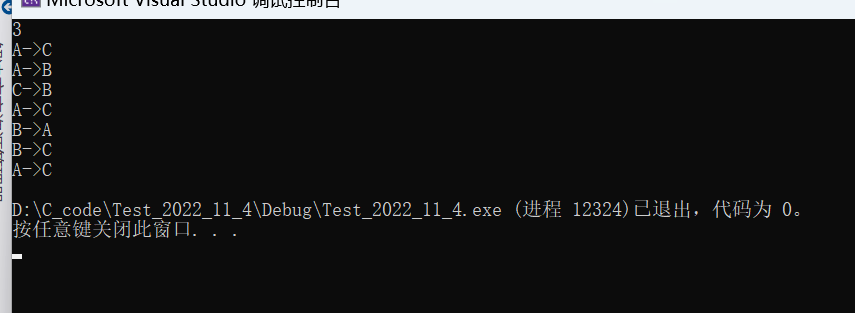
汉诺塔问题和青蛙跳台阶问题
写到这里这篇已经非常长了,由于这两个也是非常经典的问题,展开来说的话篇幅也实在不短,我们放到下一期会单独来分析。