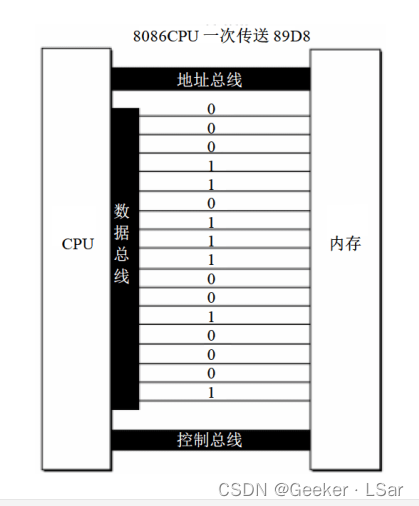
EEG-GAN: Generative adversarial networks for electroencephalograhic (EEG) brain signals

Abstract

生成对抗网络(GANs)最近在涉及图像的生成应用中非常成功，并开始应用于时间序列数据。在这里，我们将EEG- gan描述为生成脑电图(EEG)大脑信号的框架。我们引入了对Wasserstein GANs的改进训练的修改，以稳定训练并研究一系列对时间序列生成至关重要的架构选择(最显著的是向上和向下采样)。为了进行评估，我们考虑并比较不同的指标，如Inception得分、Frechet Inception距离和切片Wasserstein距离，共同表明我们的EEG- gan框架生成了自然的EEG示例。因此，它在神经科学和神经学领域开辟了一系列新的生成应用场景，例如脑机接口任务中的数据增强、脑电图超级采样或损坏数据段的恢复。产生特定类别和/或具有特定属性的信号的可能性也可能为研究大脑信号的潜在结构开辟一条新的途径。

1. Introduction

虽然机器学习的很大一部分是处理从现实数据(如分类任务)中解码信息，但最近也有一个非常活跃的领域，即如何通过隐式生成模型生成这种现实数据。例如，生成人工数据可以用于数据增强，通过生成原始数据集中不包括的自然外观的样本，从而人为地增加训练数据中的未见样本。此外，生产具有某些特性的自然外观样品的可能性，以及对模型的研究创建它们，可以成为理解用于训练GAN的原始数据分布的有用工具。GAN最近提出的生成人工数据的框架是生成对抗网络(Goodfellow等人，2014)，它显示了生成人工图像的突破性结果。最初，香草GANs严重受训练不稳定性的影响，并且仅限于低分辨率的图像。Arjovsky等人，2017;Gulrajani等人，2017;Kodali等人，2017)，并在训练期间逐步提高图像分辨率(Karras等人，2017)。GAN还允许有意地操纵生成样本中的特定属性(Radford et al.， 2015)，因此可以被证明是理解用于训练GAN的原始数据分布的有用工具。

GANs主要开发并应用于图像生成，研究时间序列的研究较少;最近，他们在生成人工音频方面展示了有希望的结果(Donahue et al.， 2018)。人工脑电图信号的生成将应用于处理解码和理解大脑信号的许多不同领域，但据我们所知，目前还没有关于用GANs生成原始脑电图信号的研究发表。

在这项工作中，我们将GAN框架应用于人工脑电图信号的生成。虽然时间序列数据的生成通常采用自回归模型(例如van den Oord等人的WaveGAN(2016))，但我们故意选择了常规卷积神经网络——一方面是因为大多数GAN研究使用基于cnn的DCGAN (Radford等人，2015)架构，另一方面是因为cnn的局部和层次结构可能允许更好的可解释性(Sturm等人，2016;Kindermans等人，2017;Schirrmeister等人，2017;Hartmann等人，2018)，这对神经科学或临床背景下的大脑信号尤为重要。

为了生成脑电图数据的自然样本，我们提出了对Wasserstein GAN训练的改进，显示出更高的训练稳定性。此外，我们比较了不同的评价指标，并讨论了方法和网络的架构选择在本研究中交付了最好的结果。

2. Methods

2.1. GAN background and improvementGAN背景及改进

GAN框架由两个相互对立的网络组成，试图击败对方(Goodfellow等人，2014)。第一个网络，鉴别器，被训练来区分真实和虚假的输入数据。第二个网络是生成器，它将潜在噪声变量z作为输入，并尝试生成鉴别器无法识别的假样本。这导致了一个极大极小博弈，其中生成器被鉴别器强迫产生更好的样本。

GANs的一个大缺点是训练期间鉴别器的臭名昭著的不稳定性。鉴别器可能会崩溃，只识别输入分布的少数和狭窄的模式为实，这驱使生成器只产生有限数量的不同输出。Arjovsky等人，2017;Gulrajani等人，2017;Kodali等人，2017)。

Wasserstein GANs和Arjovsky等人(2017)提出的改进版本在训练稳定性方面取得了有希望的进展。原始GAN框架试图最小化真实数据分布Pr和虚假数据分布Pθ之间的Jensen-Shannon (JS)发散(Goodfellow et al.， 2014)。如果鉴别器被训练为最优，这可能会导致生成器的梯度消失问题(Arjovsky等人，2017)。Arjovsky等人(2017)提出最小化分布之间的Wasserstein距离，而不是js散度。这导致鉴别器(现在称为批评家)将差异最大化。

 且发生器使Exf ~ Pθ[D(xf)]最大化。他们表明，如果D(x)是K-Lipschitz，则该临界为生成器提供了一个有用的梯度。在他们的原始论文中，他们通过将鉴别器的权值剪辑到区间[- c, c] (WGANclip)来加强Lipschitz连续性，但后来通过添加梯度惩罚项得到了更优雅的解决方案

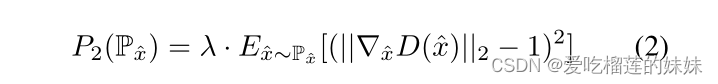
P‑x包含位于真实样本和生成样本之间的直线上的点，到临界损失(Gulrajani等人，2017)。

在训练带有梯度惩罚的WGAN-GP时，λ的选择是至关重要的。如果λ选得过高，惩罚项很容易支配距离项。反过来说，如果λ选得太小，李普希兹连续性就不能充分实现。我们注意到λ的一个好的选择很大程度上取决于Pr和Pθ之间的距离。如果距离很高，λ必须选择相应的高。如果它们是接近的，λ必须选择相应的低。然而，在训练过程中，生成器学习近似Pr。这导致Pr和Pθ之间的距离减小，而λ保持不变。

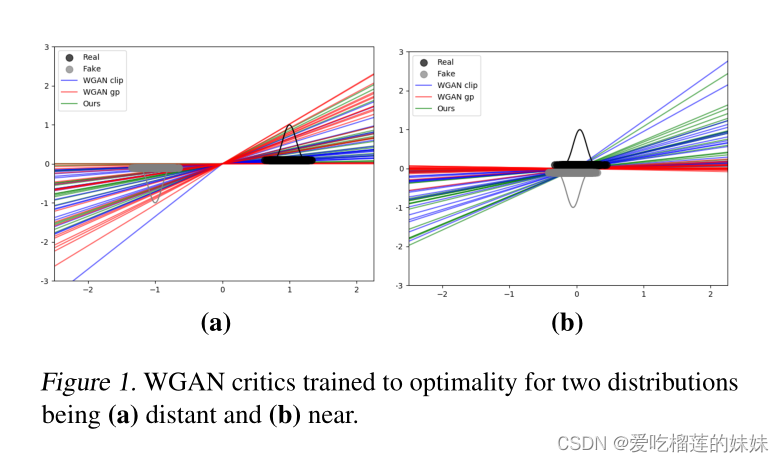
 图1 WGAN判别器训练为两个分布的最优(a)远(b)近。

图1a显示了训练有素的WGAN-clip和WGAN-GP判别器，以区分两个正态分布。参数c和λ的选择使得评论家提供了一个有用的梯度，并且对于大多数评论家来说||∇xD(x)||2 <= 1。图1b再次显示了判别器使用相同的参数设置训练来区分两个分布，但现在它们之间的距离缩短了。这模拟了Pθ与Pr的近似。WGAN-GP评论家明显地崩溃为消失的梯度，在一些情况下显示Exf∼Pθ[D(xf)] > Exr∼Pr[D(xr)]。具有权值剪辑的WGAN保持稳定，因为它的唯一目标是通过限制网络权值来最大化正则化的临界差。然而，限制权重会导致网络参数不希望收敛到这些极限(Gulrajani et al.2017)。

 

因此，我们提出对WGAN-GP进行改进，逐步放宽梯度约束。我们不仅用λ对惩罚项进行加权，还通过当前判别器差异~ W (Pr, Pθ)对其进行缩放。因此，惩罚项只有在满足判别器区分Pr和Pθ的第一个目标，并且λ被缩小以减少分布距离时才会被严格执行。此外，我们将不使用Gulrajani et al.(2017)推荐的双侧惩罚P2(P x)，而是使用单边惩罚

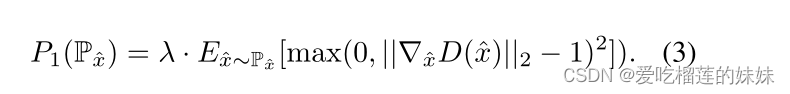
他们没有说明选择双侧惩罚而不是单侧惩罚的具体原因，但从经验结果来看，他们更倾向于选择双侧惩罚。由此得出的判别器的损失函数则成为

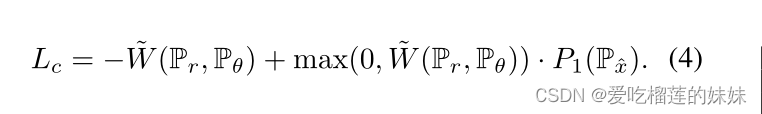
用这种损失训练出来的判别器对距离递减的分布表现出稳定的梯度（图1）。

2.2. Training and architecture choices训练和结构选择

我们根据Karras等人（2017）中描述的设置来训练我们的网络。 他们表明，随着分辨率的提高，通过逐步训练网络，可以提高生成的图像质量。因此，我们从24个时间样本的分辨率开始，在6个步骤中以系数2增加分辨率，到达768个样本。因子2引入了最少的频率伪影，导致了最好的结果。我们加入了Karras等人（2017）的额外技术，如最小批量标准偏差、均衡学习率和像素归一化。而不是他们提出的额外惩罚项以防止批评家离0太远，我们使用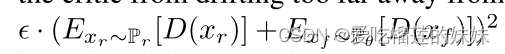其中∈=0.001，以保持判别器在0的中心。

与Karras等人（2017）的做法相反，我们不对判别器和生成器进行同等的训练，而是先对判别器进行训练，直到最优为止（按Arjovsky等人（2017）最初的建议，通过5次判别器迭代）。我们设置λ=10，正如Gulrajani等人（2017）最初提出的那样）每个解析阶段训练2000个历时（相当于876.000次信号显示），每个阶段还有2000个历时用于消退。网络使用ADAM优化器（Kingma & Ba, 2014）训练，lr = 0.001，β1 = 0，β2 = 0.99。生成器的潜变量z从N（0，1）中取样。

我们的网络结构可以在表1中看到。生成器中的每个上采样块由一个上采样层和两个大小为9的卷积层组成。同样地，每个判别器由2个卷积层和1个下采样层组成。对于下采样，我们使用平均池化和跨度为2的跨度卷积。我们在判别器和生成器中使用 leaky ReLU 来避免稀疏梯度。

对于上采样，我们比较了近邻上采样以及线性和立方插值。正如Donahue等人（2018）所说，上采样总是会引入混叠频率伪影。虽然他们认为这些伪影可能是产生细粒度细节所必需的，但我们认为它不必要地使生成器的训练复杂化，至少在脑电信号的情况下。近邻上采样引入了强烈的高频伪影，而线性或立方插值导致的伪影要弱得多（图2）。我们认为这是有利的，因为我们不希望生成器在上采样后过滤掉伪影，而是预计会产生额外的高频特征。

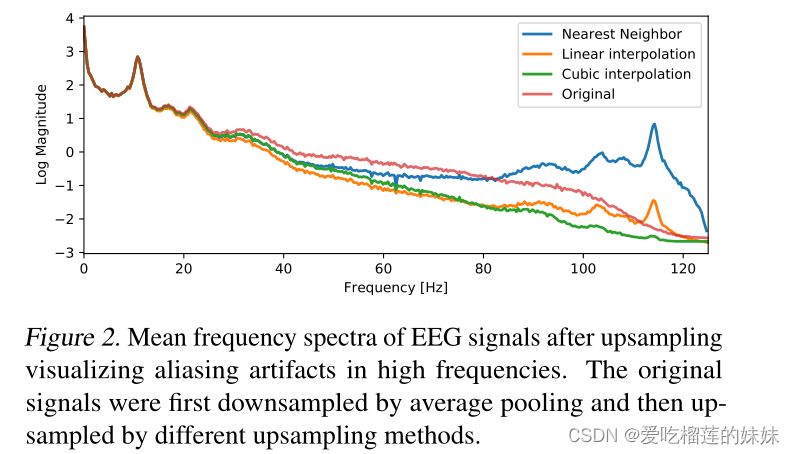
图2  高频混叠伪影上采样后脑电图信号的平均频谱。首先对原始信号进行平均池化下采样，然后采用不同的上采样方法进行上采样。

2.3. Evaluation metrics 评价指标

2.3.1. INCEPTION SCORE初始得分

对生成器产生的样本分布的评估是一个持续的挑战。对生成的样本进行目测有助于识别明显的故障和模式崩溃，但无法提供任何关于生成样本的差异以及它们与训练数据的相似程度的定量信息。一个常用的方法是使用初始分数（IS）来给出关于训练生成器质量的信息（Salimans等人，2016）。

为了计算初始分数，在训练数据上训练分类器，并用于确定生成样本的条件标签分布的熵（应该很低）和它们的边际熵（应该很高）。虽然初始得分被证明与作者注释有很好的相关性，但它不能提供关于生成器质量的有用信息。

起始得分对噪音高度敏感，并且不能检测模式崩溃，因为它完全依赖于分类器的最终概率。我们使用预先训练好的Deep4模型（Schirrmeister等人，2017）作为脑电图数据的初始模型的替代。

 2.3.2. FRECHET INCEPTION DISTANCE 弗雷歇起始距离

Frechet起始距离(FID) (Heusel et al.， 2017)旨在更好地评估生成样本的质量，是一个合适的距离。与初始评分类似，FID也使用训练过的分类器。但是，FID不是简单地评估生成样本的类别概率分布，而是比较真实样本和生成样本在嵌入层(即最终分类层之前的层)中的值。Frechet距离用于计算真实样本和假样本嵌入层中值分布之间的Wasserstein2距离，假设它们遵循多元高斯分布。Heusel等人已经证明FID与人类判断一致，并且与初始评分相比，对噪声更稳健，提供了关于生成样本质量的信息，并对模式崩溃敏感。然而，它也不能检测生成器对训练样本的过拟合。

 2.3.3. EUCLIDEAN DISTANCE欧式距离

欧几里得距离可以用来评估生成的样本与训练数据的相似程度。通过比较生成样本和真实样本之间的距离，我们可以研究生成器只是从训练集中复制样本或产生一些看不见的东西，生成模型通常不会评估这个属性，但对我们来说尤其重要，因为与非常大的图像数据集相比，我们的训练样本数量更少。最优情况下，真实样本和虚假样本之间的最小距离分布(EDmin)应该等价于真实样本与其他样本之间的最小距离分布。

2.3.4. SLICED WASSERSTEIN DISTANCE切片瓦瑟斯坦距离

 瓦瑟斯坦距离描述了在给定的成本函数下将一个分布转换为另一个分布的成本(参见(Peyr´e & Cuturi, 2018)以获得更详细的解释和概述)。切片瓦瑟斯坦距离(SWD)是使用1d投影的瓦瑟斯坦距离的近似值。它通过计算两个分布的所有一维投影(切片)之间的瓦瑟斯坦距离来近似瓦瑟斯坦距离。这种方法具有闭形式解和相应的一维情况快速计算的优点。在实践中，切片的Wasserstein距离本身是通过使用有限的随机1d投影集来近似的(Rabin et al.， 2012)。低切片的Wasserstein距离表明，两种分布在外观和样本的变化上是相似的。

 3. Data

我们将用于训练的脑电图信号来自一个简单的运动任务，在这个任务中，受试者被指示休息或移动左手。用128电极脑电图系统记录信号，并将采样降至250 Hz。

受试者在alpha、beta和高gamma范围内显示了电极通道FCC4h左手运动的特征光谱信息。在这里，我们将只使用通道FCC4h来训练GAN。通过减去平均值，然后除以最大绝对值，将数据集缩放为[−1,1]。总体而言，数据集包含438个信号，其中286个信号将用作初始分类器的训练数据，72个信号作为验证数据，80个信号作为测试集。所有438个信号将用于训练GAN。

4. Results

4.1. Distance results

表2显示了使用我们的方法(1-4)和原始WGANGP(5)训练的不同架构的度量结果。VG表示通过平均池化进行下采样，CONV表示通过跨步卷积进行下采样。对于上采样，NN表示最近邻，LIN线性插值和CUB三次插值。用于计算启始评分和Frechet启始距离的启始分类器的测试准确率为91.25%。真实数据和噪声(从真实数据的均值和方差的正态分布中采样)的分数被列出用于比较。

 

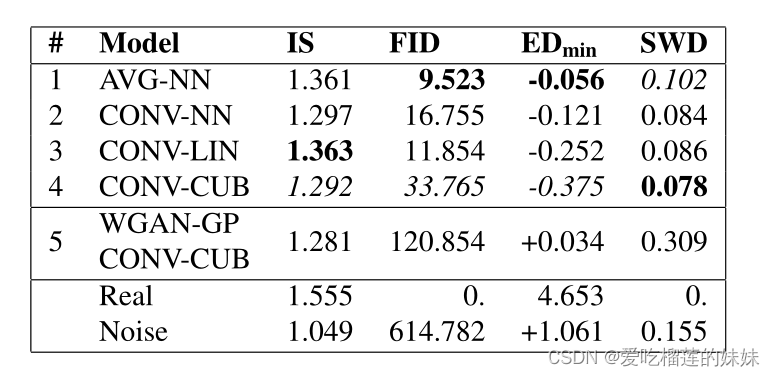
表2。不同体系结构的GANs的结果。VG表示平均池化，CONV跨步卷积表示下采样。NN为最近邻上采样，LIN为线性插值，CUB为三次插值。除WGAN-GP外，其余模型均采用本方法训练。WGAN-GP在训练中崩溃。最好的分数用粗体标出，最差的分数用斜体字体标出。

从视觉检查、FID和切片Wasserstein距离来看，很明显WGAN-GP模型崩溃了，尽管我们必须注意到，我们既没有执行任何超参数搜索，也没有多次运行以找到一个工作模型。然而，对于用我们的方法训练的模型，我们也没有这样做，尽管它们在性能上有所不同，但它们都没有崩溃。IS没有给出该模型崩溃的有力证据。

对于用我们的方法训练的模型，不同的架构对于不同的指标表现最好。convi - lin在IS中表现最好，VG-NN紧随其后。对于FID, VG-NN确实表现最好，convc - cub明显最差。EDmin是最接近真正的EDmin对于一个VG-NN, convc - cub是最差的。然而，对于SWD, CONV -CUB显然是最好的，而A VG-NN显然是表现最差的模型。总的来说，CONV -CUB是除SWD外所有指标表现最差的模型。

4.2. Visual inspection目测

4.2.1. TIME SAMPLES 时间样本

图3显示了由我们的模型训练的4个架构创建的信号与真实信号的平均值和标准差。样本在每个时间点的相似性从体系结构1增加到体系结构4。而VG-NN显示出生成的样本分布与真实数据的明显偏差，CONV -CUB显示出非常好的拟合。

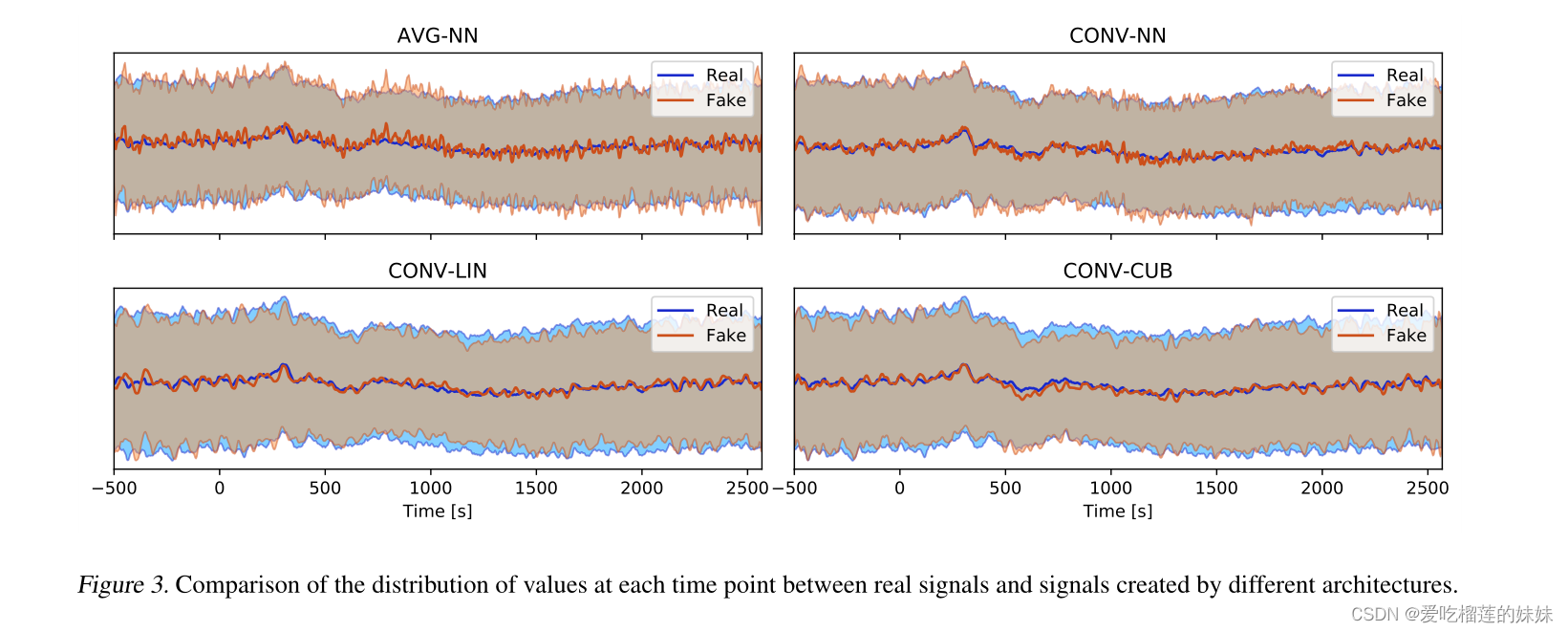
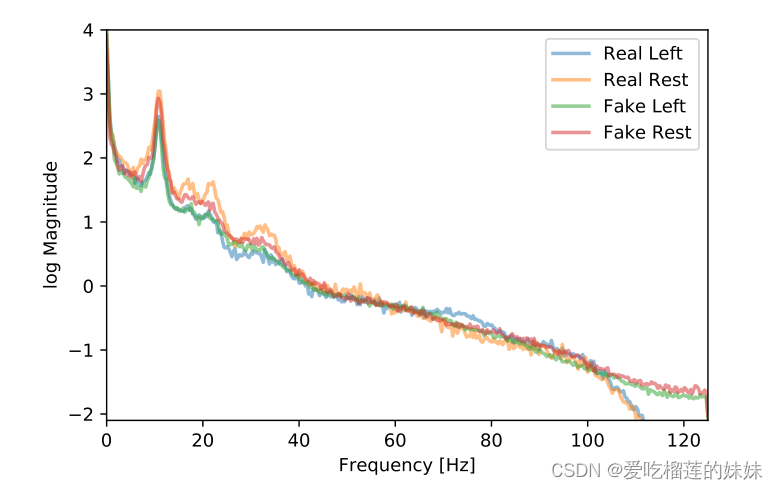
4.2.2. FREQUENCY SPECTRA 频率谱

 类似地，图4显示了频率分辨光谱功率分布的比较。VG-NN和CONV NN即使在低频也显示出与真实频谱的偏差，而convn - lin和convn - cub再次显示出良好的拟合。可以说，convi - lin更适合低频，而convi - lin更适合高频。没有任何模型能够正确地适应高于100赫兹的频率(然而，这种频率的功率非常低)。

 4.2.3. GENERATED SAMPLES 生成样本

 

图5为A VG-NN和CONV -CUB生成的随机样本。这两个模型都是可视化生成的声音信号。信号之间的一个显著区别是convc - cub通常只生成包含弱振荡序列的信号。当通过与真实信号进行视觉比较时，这些序列对假信号具有高度指示性。

4.3. Class-specific properties 特定类别的属性

为了研究CONV-CUB生成的信号的特定类别属性，我们使用初始分类器来确定被分类为属于任一类别的信号，准确率>90%。同样地，我们用同样的方法来确定表现为任一类别的概率>90%的真实信号。图6中显示了各自频率谱的比较。被归类为左手运动的生成信号与真实信号中阿尔法和贝塔活动的减少相匹配，直到40Hz左右。生成的左手信号虽然没有表现出在真实的左手信号中存在的高伽马活动信号的增加。

 

5. Discussion & Conclusion讨论与结论

通过这项工作，我们表明有可能用生成式对抗网络生成人工EEG信号。

通过对改进的WGAN训练的修改（Gulrajani等人，2017），我们能够逐步训练GAN，以稳定的方式产生人工信号，在时域和频域上与单通道的真实EEG信号非常相似。

我们通过与各种指标的比较，评估了上采样和下采样的几种选择的优点和缺点。在我们的案例中，初始得分（IS）（Salimans等人，2016）并没有提供关于模型生成的信号质量的有意义的信息。此外，我们观察到，具有最低Frechet inception distances（FID）（Heusel等人，2017）的模型不一定能产生与真实输入样本相似的空间和光谱特性的信号。根据空间和光谱特性产生最自然分布的信号的模型被赋予最差的FID。因此，用于脑电图的GANs向好的IS或FID的优化可能会导致产生被错误地认为与真实数据相似的信号分布。表达最自然的空间和光谱分布的模型具有最好的切片瓦瑟斯坦距离（SWD）。较低的欧氏距离表明生成器对特定的训练样本有偏好，尽管在我们的案例中，它没有低到表明训练样本的简单再现。总的来说，没有一个单一的指标能够提供关于模型质量的足够信息，但是FID、SWD和ED的组合能够很好地说明其可能的整体属性。因此，我们不推荐任何单一指标，而是鼓励使用具有不同优势和劣势的几个指标。

6. Outlook展望

随着人工脑电信号生成的第一步完成，现在有许多进一步调查的开放可能性。当然，下一步不仅要生成单通道信号，还要对完整的多通道EEG记录进行建模。为此，进一步了解不同的设计选择，如卷积大小和上采样和下采样技术的影响将是很重要的。在我们的实验中，我们注意到卷积大小对生成器正确表达的频率范围有很大影响。此外，我们目前正在将我们的模型应用于来自不同受试者的大量脑电图记录样本，并将由医学专家小组评估所产生信号的质量。

总之，EEG-GANs为新的应用提供了可能性，不仅限于数据的增加，而且例如

空间或时间上的超级采样（Corley和Huang，2018年）或恢复被破坏的信号。产生某类信号和/或具有特定属性的信号的可能性也可能为研究大脑信号的基本结构开辟一条新途径。