1.1集合

1.2 函数

1.4数列极限

1.5函数的极限

1.6无穷小和无穷大

1.7极限的运算准则

1.8极限存在准则

定义一：夹逼定理

夹逼定理的例题

夹逼定理 不一定要用，因为你不知道左右边找哪个！！！

 定义二：单调有界数列必有极限

1.8两个重要极限

第一个重要极限

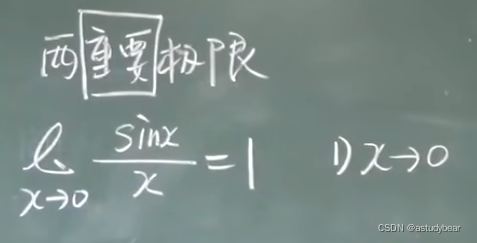
使用条件一：x一定是趋于0的

怎么用这两个极限呢，凑！凑成这两个重要函数 

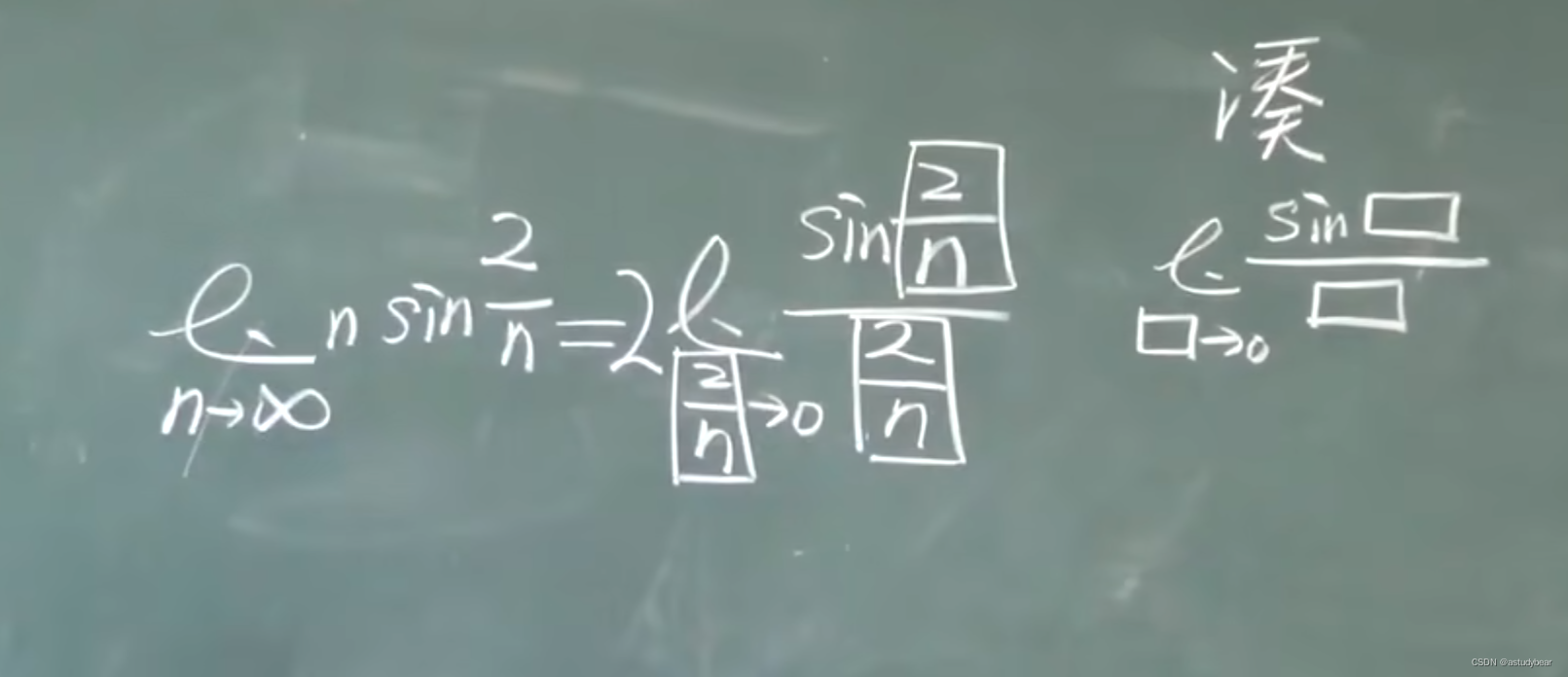
 例题二：

 例题三：

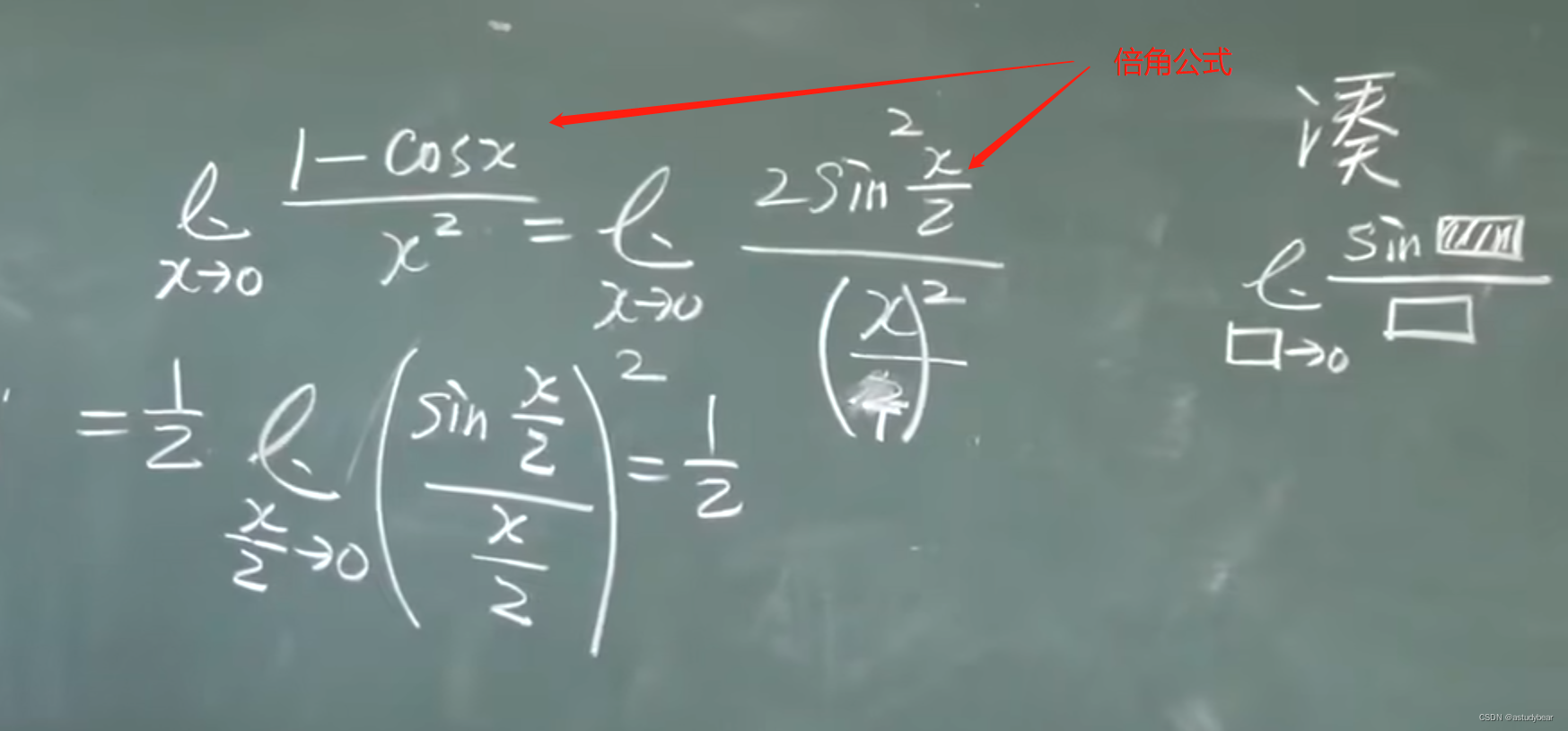
例题四：

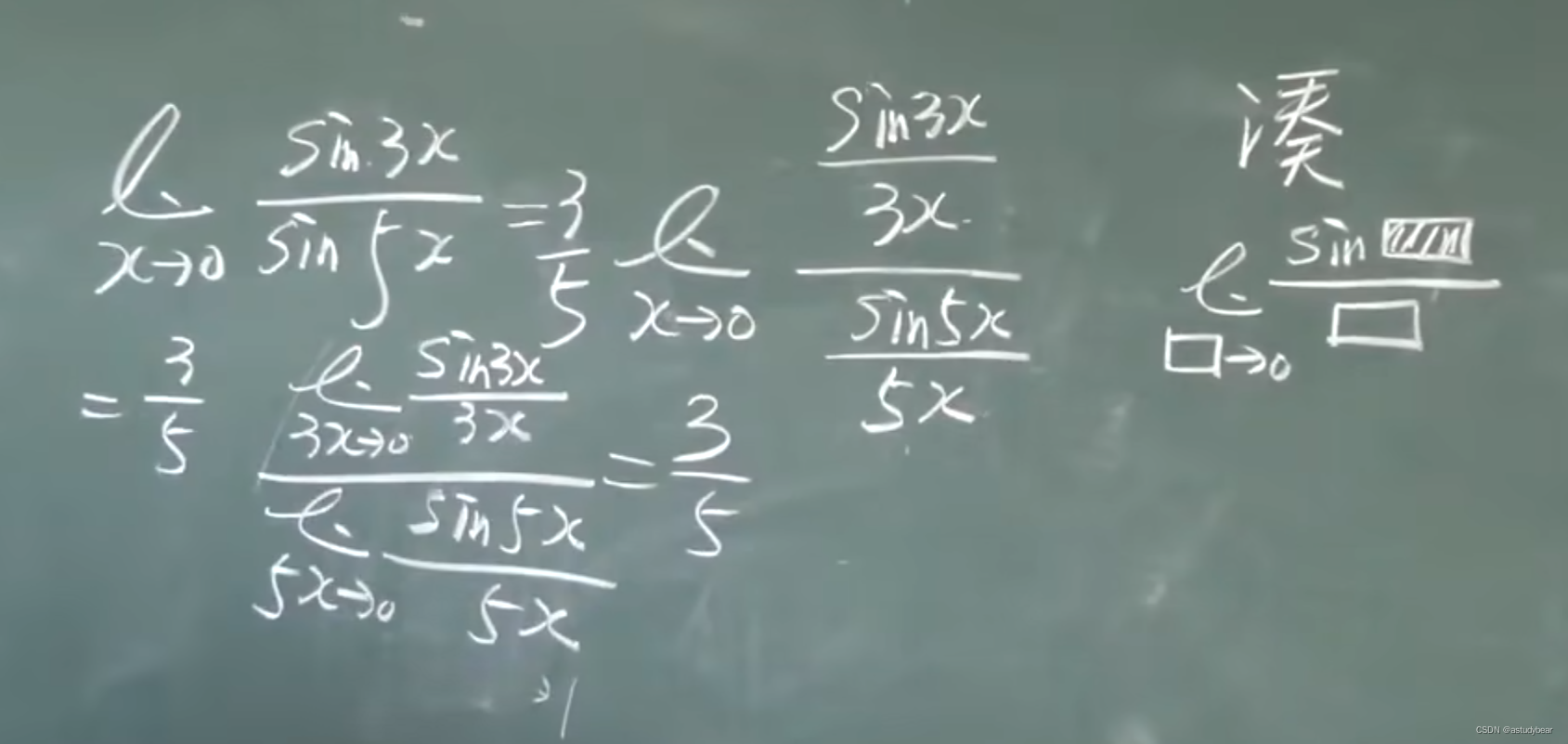 例题五：

？？？ 

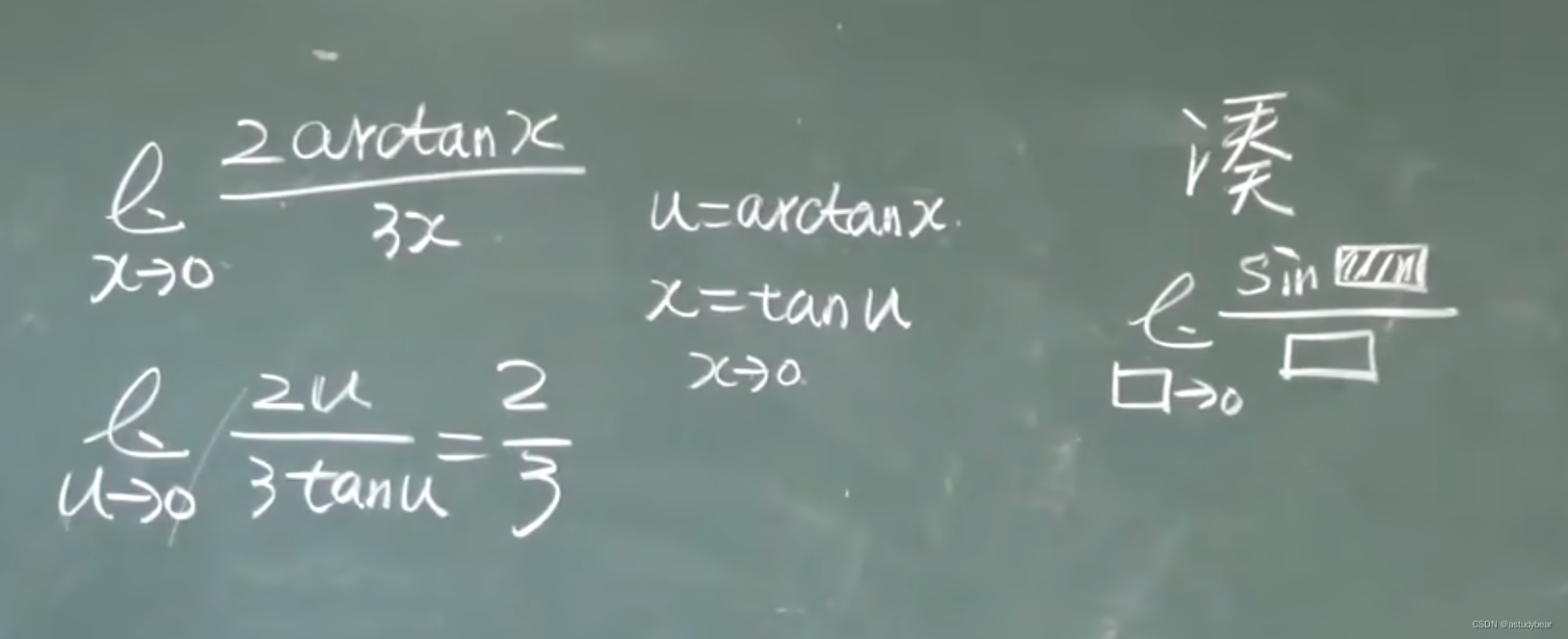题型解析：

1.上下都是sin的没有x，你得去凑

2.有tan和arctan和有cos没有sin的你怎么去处理 

第二个重要极限 

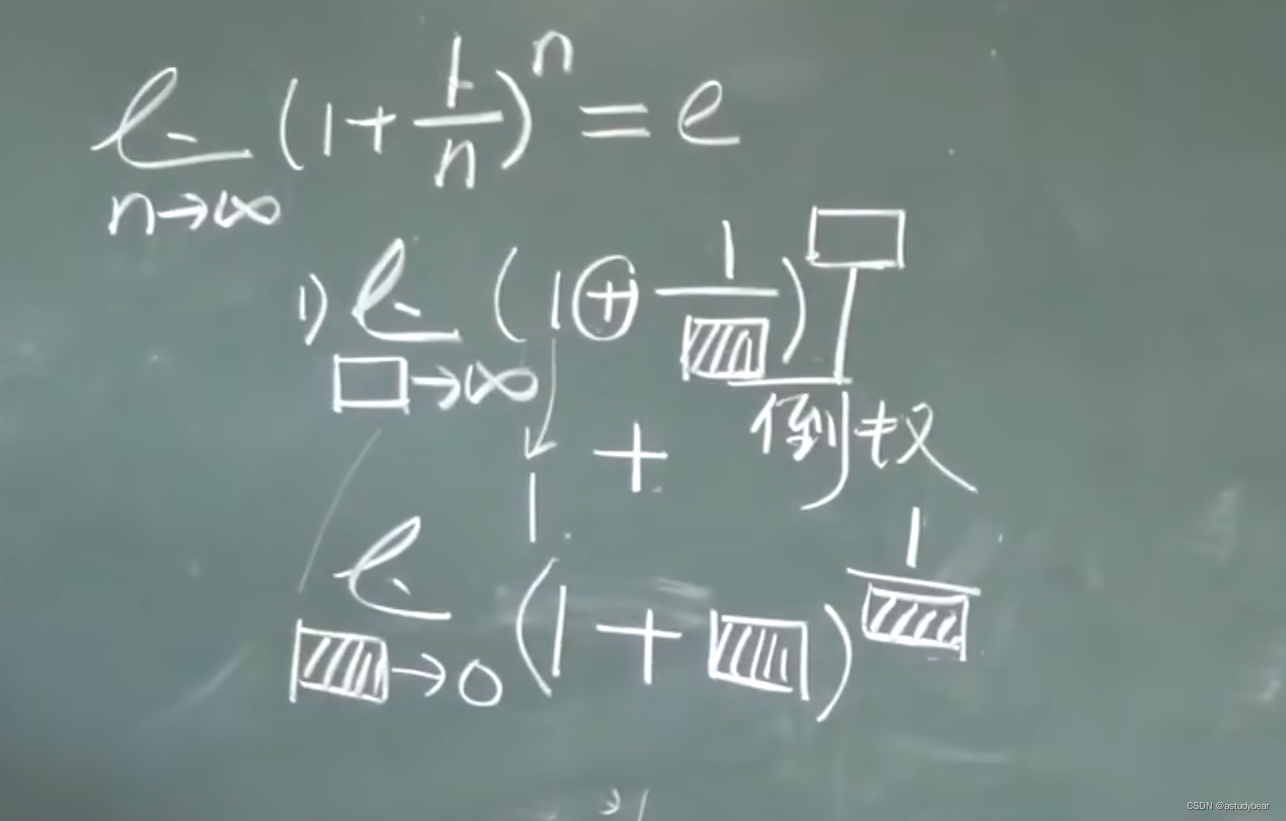
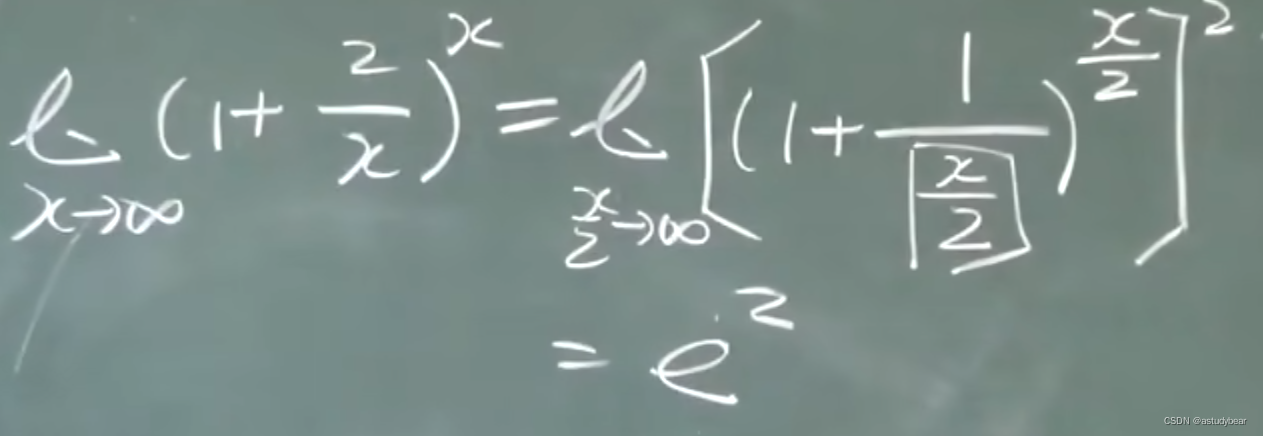
 例题二：

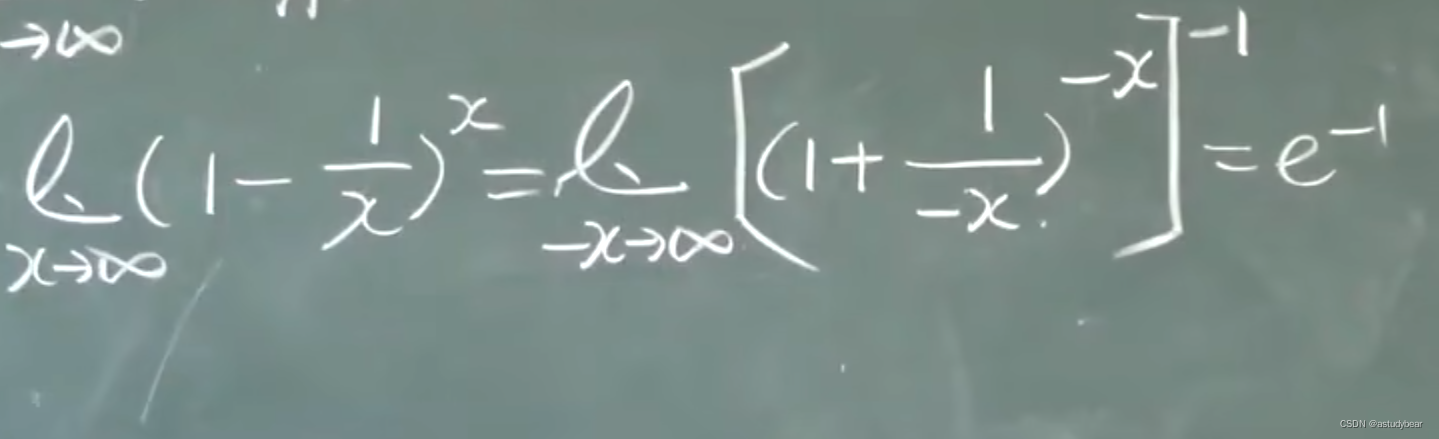
 例题三：

解法一

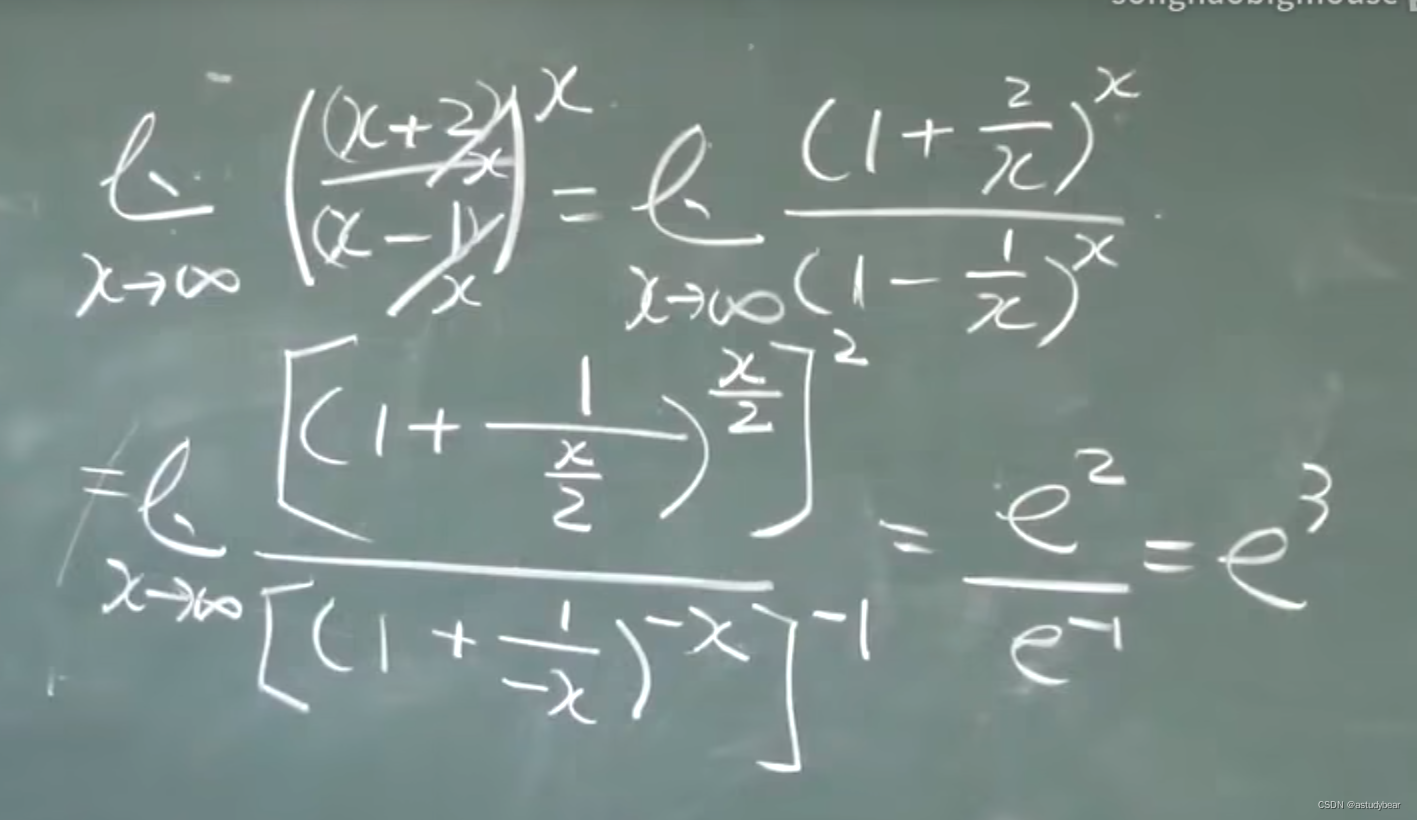
解法二

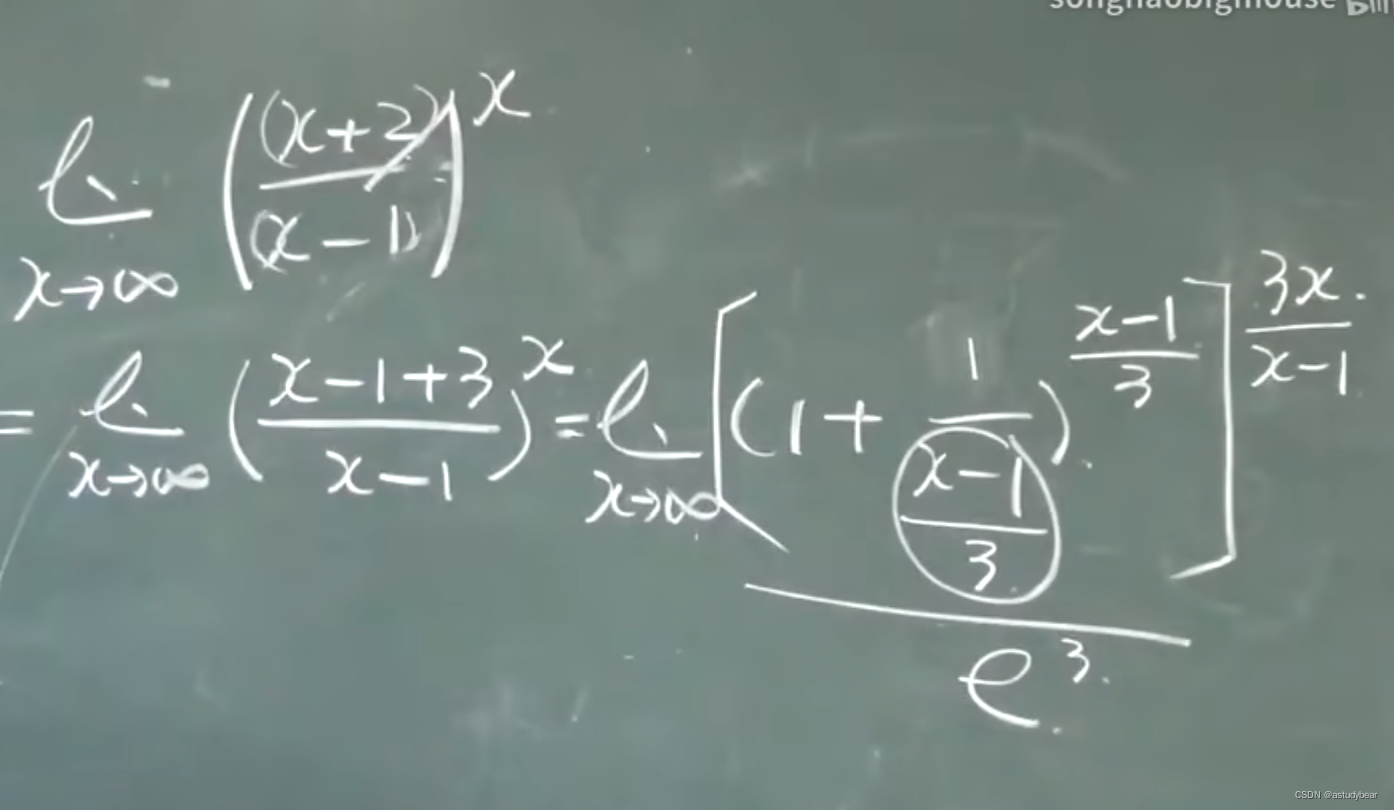
例题五：

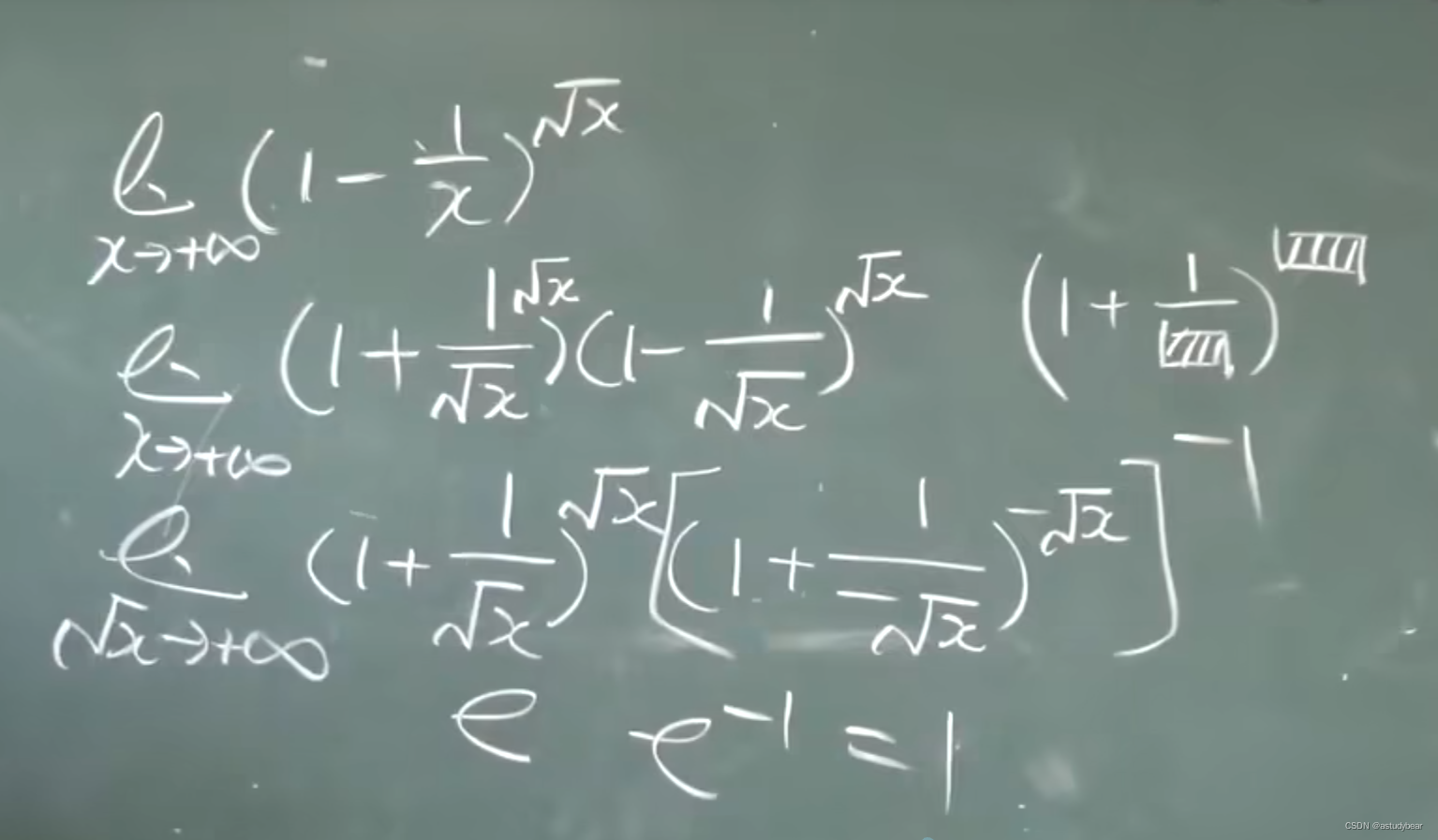
1.9无穷小的比较

     

例题一 

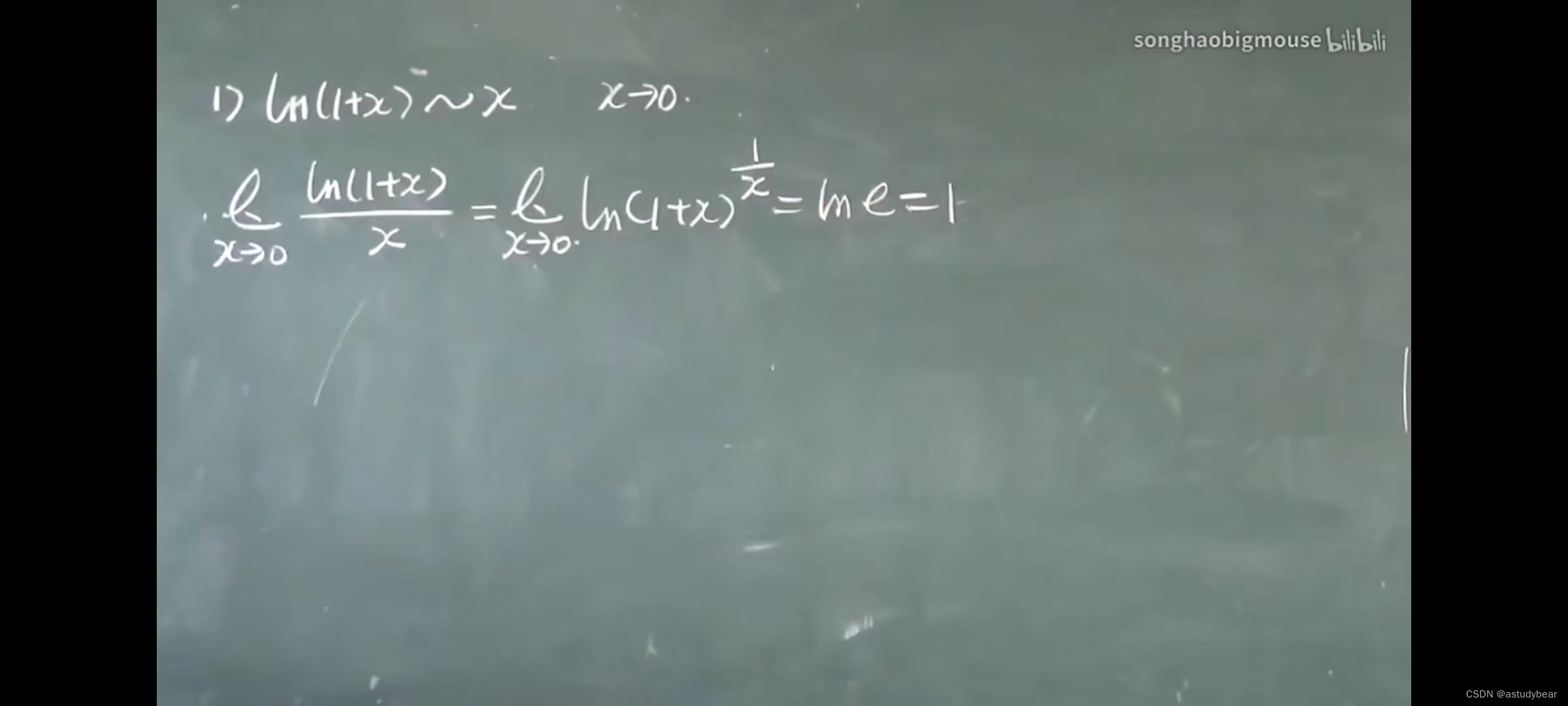
例题二

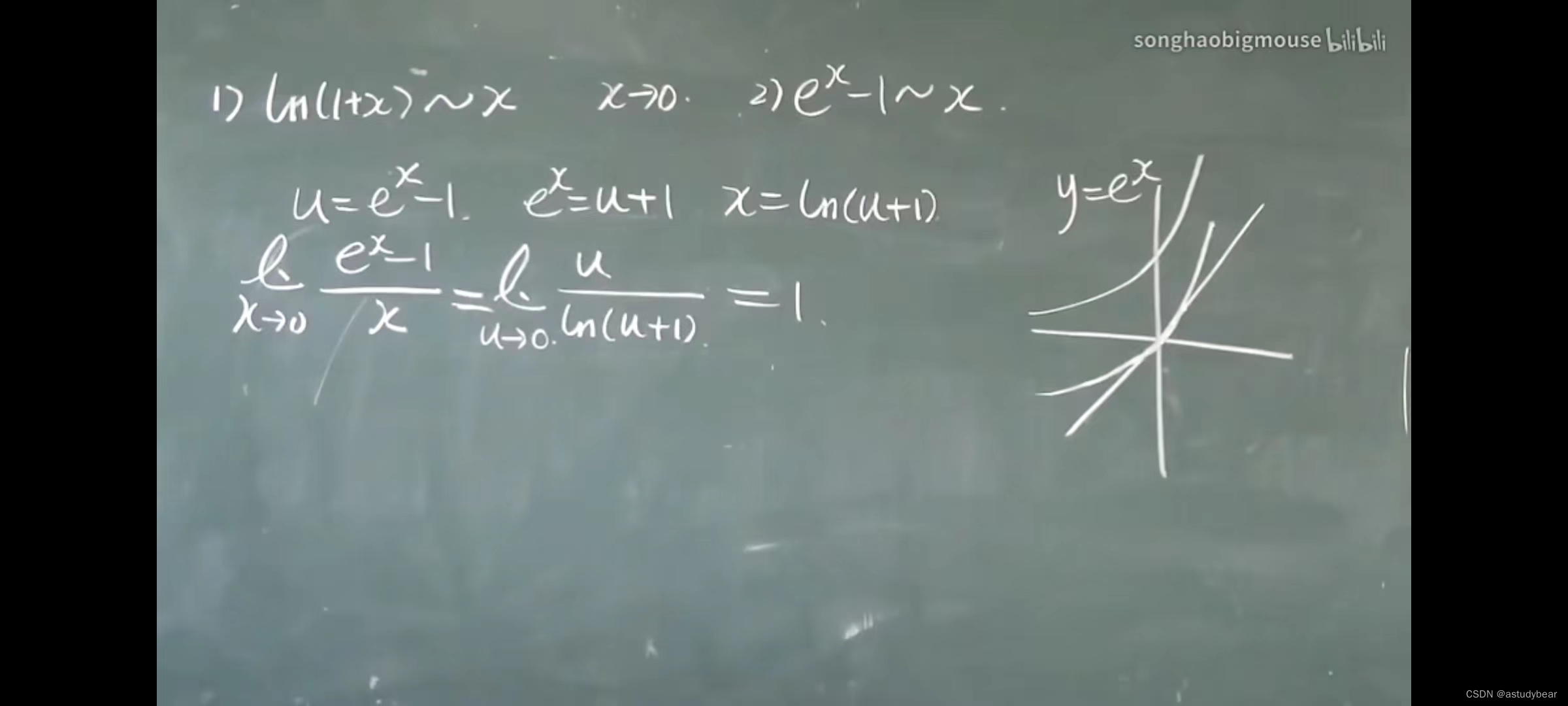
例题三

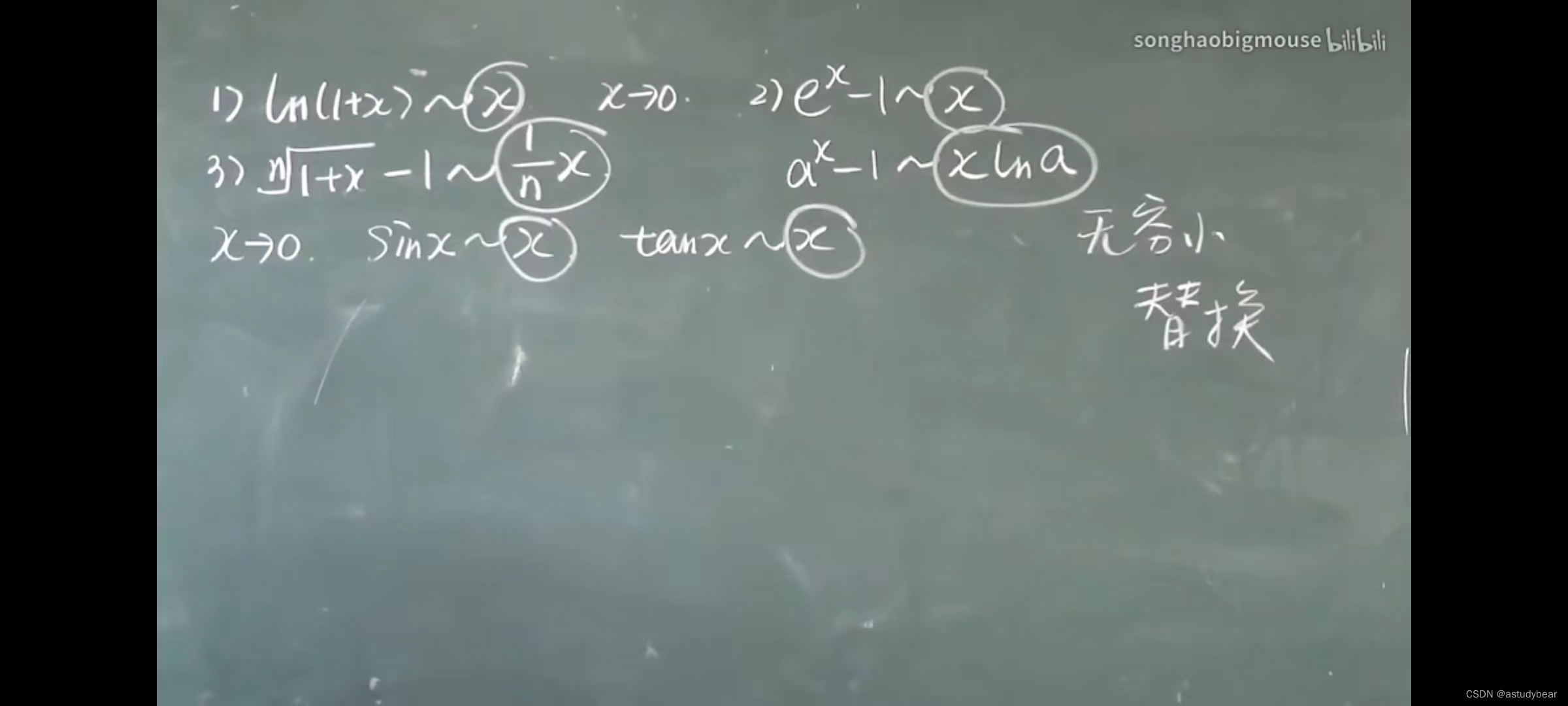
 无穷小替换的应用：

无穷小替换，求极限的时候看你趋向于多少，是可以直接无穷小替换的

可以用无穷小替换来证明极限相等

 使用的前提是:

 求极限有几种情况，一就是两个极限，二是无穷小替换，三是洛必达，四是化简并带入

例题四

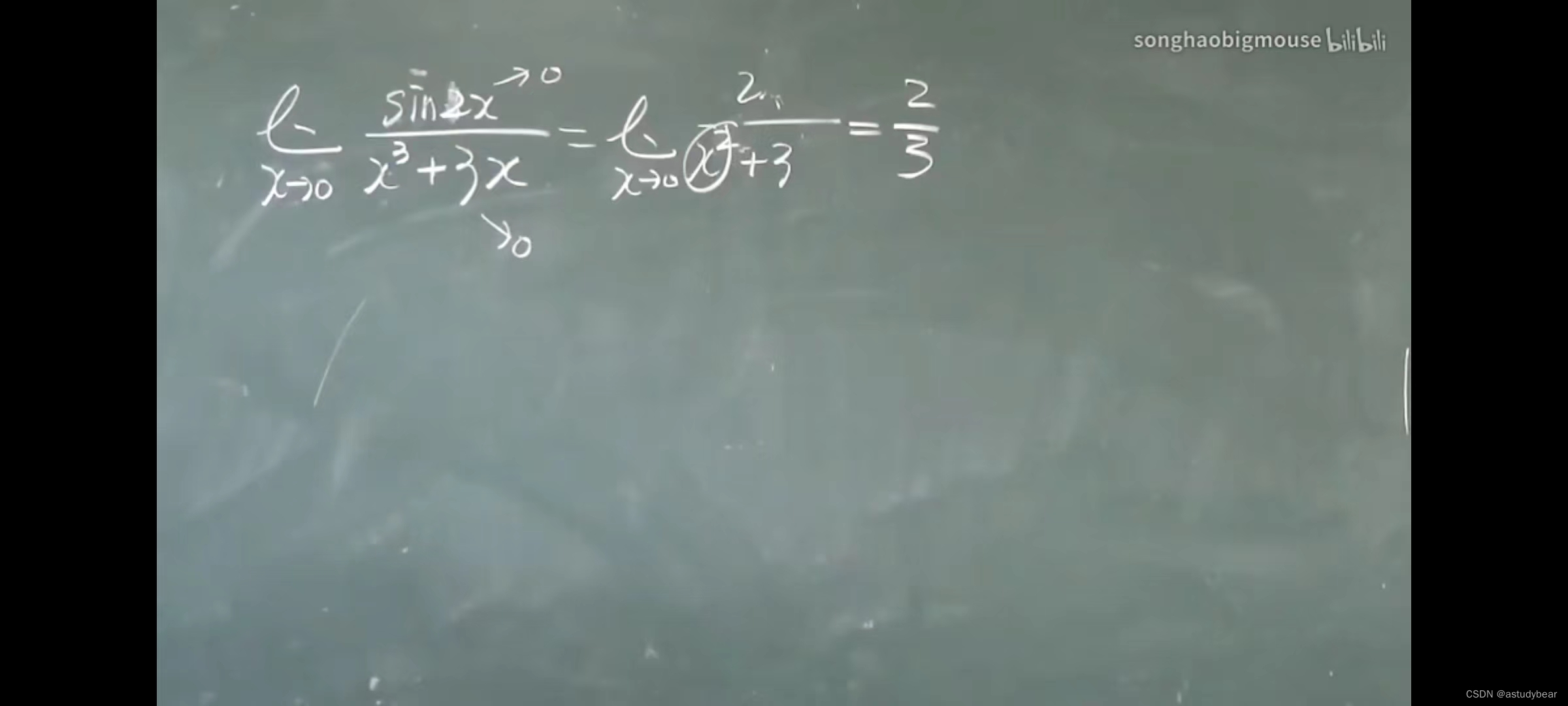
例题五

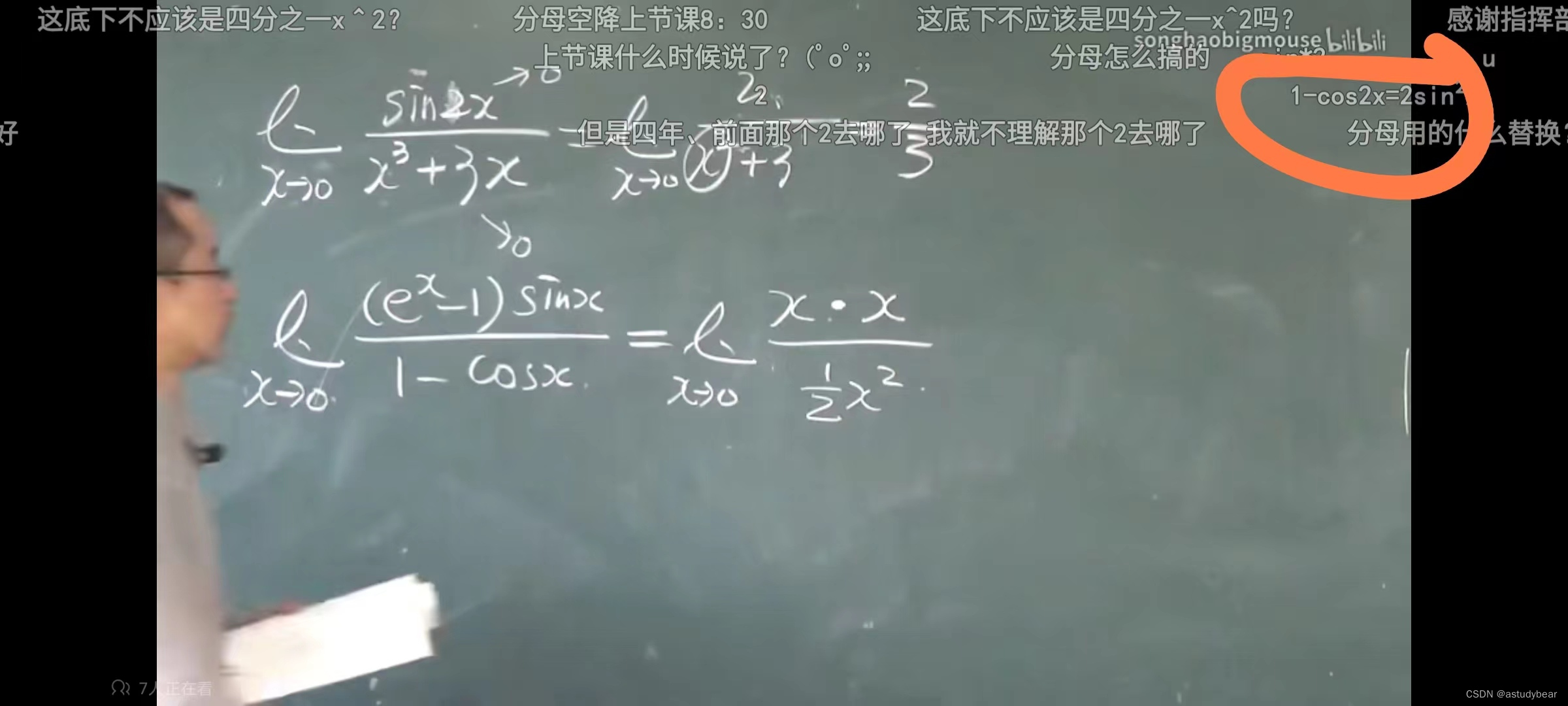
1.10函数的连续性 

如何定义连续性，就是x越小y也一定越小

连续性的定义和条件

 左右连续

区间连续

考点：连续性的考点在于证明它是连续的（基本不考）

间断点

条件：

        1）x0有定义

        2）x到x0有极限

        3）极限=定义

三条条件有一条不满足都证明是间断点，三条都满足的话就连续

考点：它是什么类型的间断点

一共有四种间断点：

        可去、振荡、跳跃、无穷

第一类间断点的定义是：左右极限均存在（可以不想等）

第二类的定义是：除了第一类都是第二类 

小技巧：一笔画（能够一笔画的函数都是连续的）

例题1：左右间断点不相等

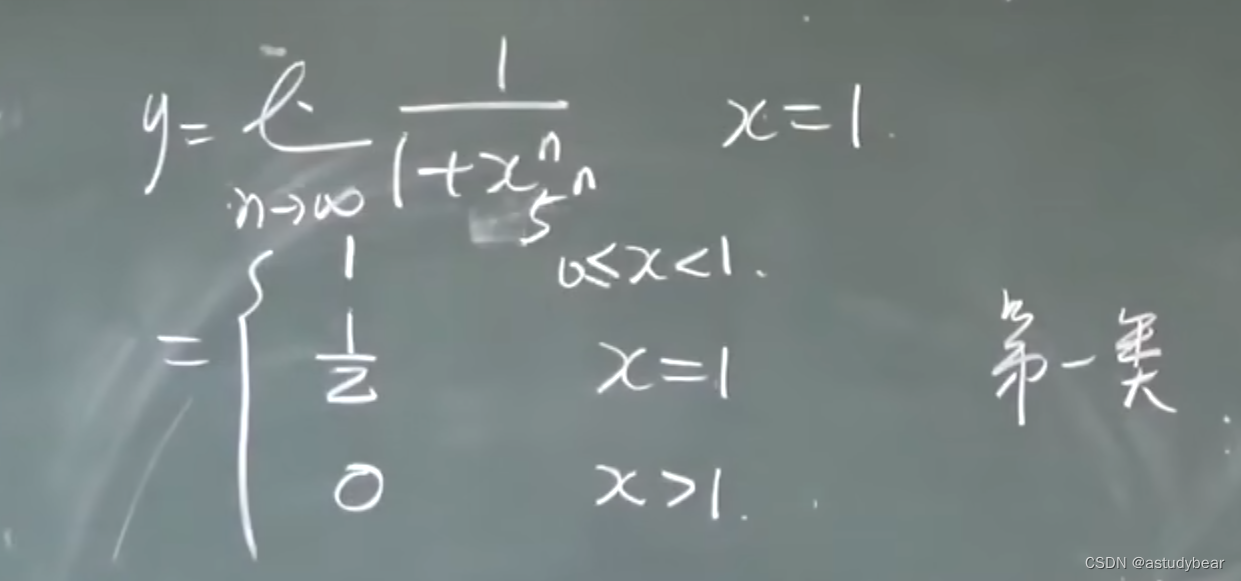
例题1：（重要考点，考选择、填空）

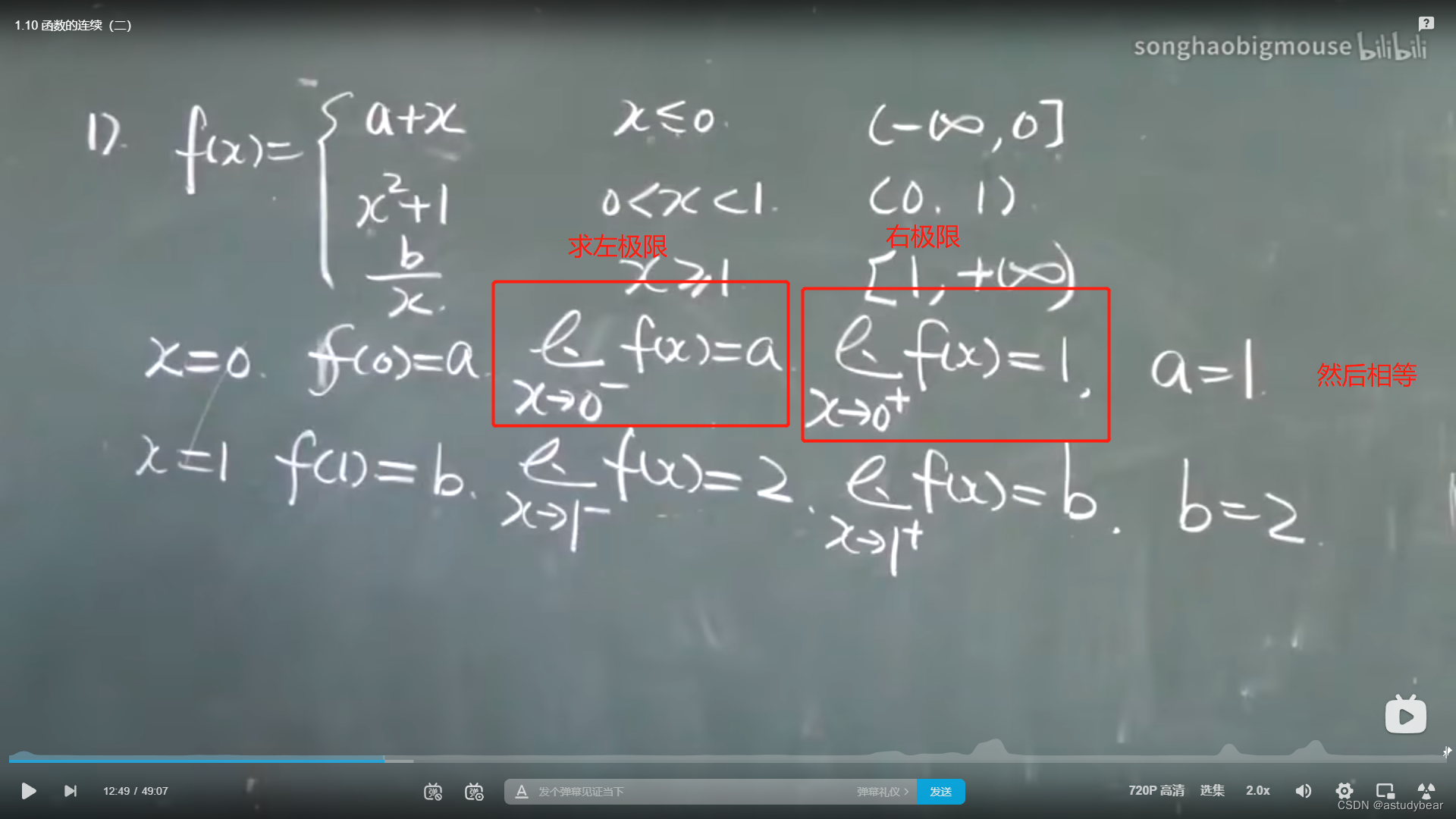 例题2：（还可以和重要函数联合）

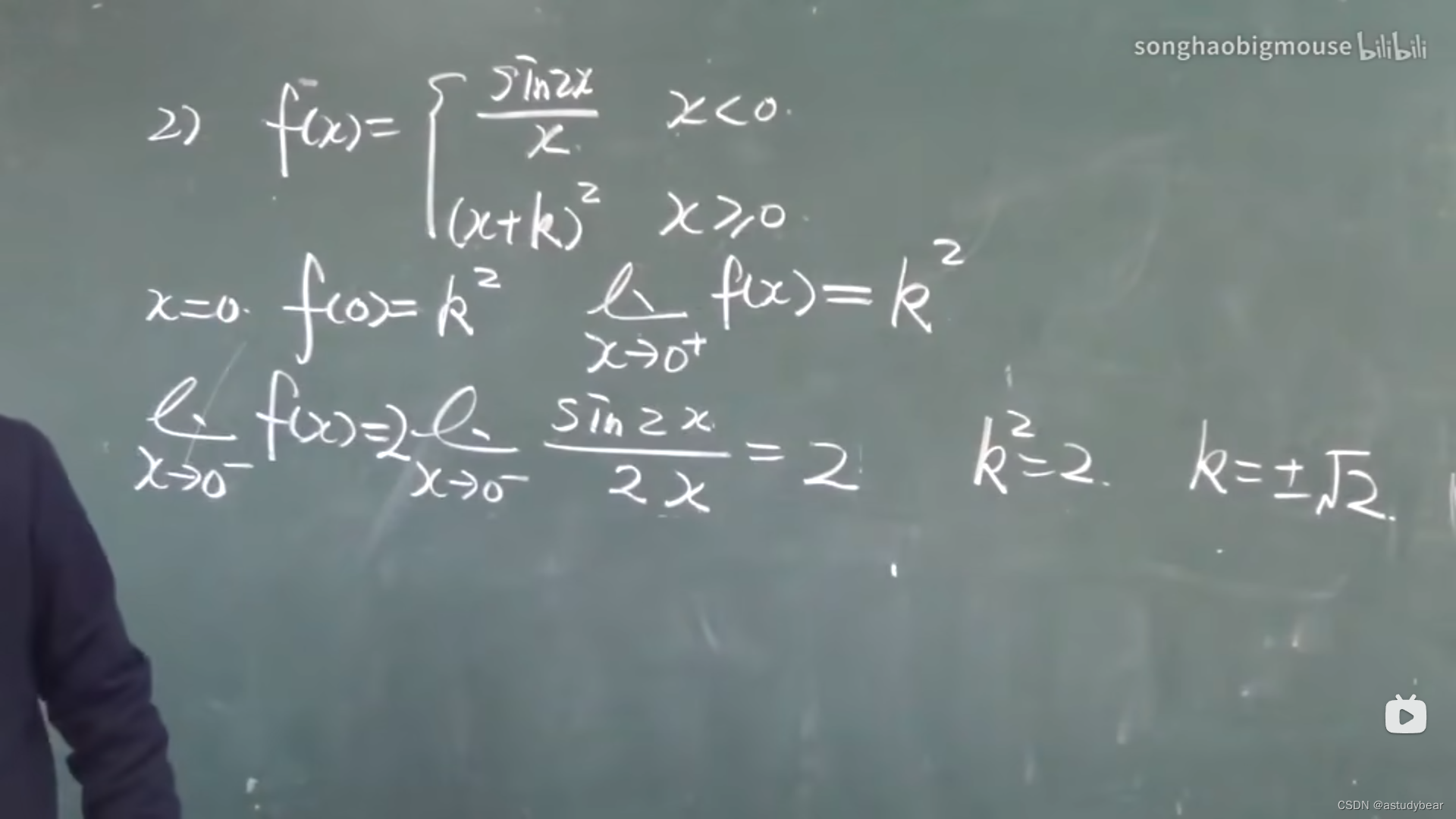
例题3、4：（例题4用到了复合函数的连续性，直接用就好了，不用说明） 

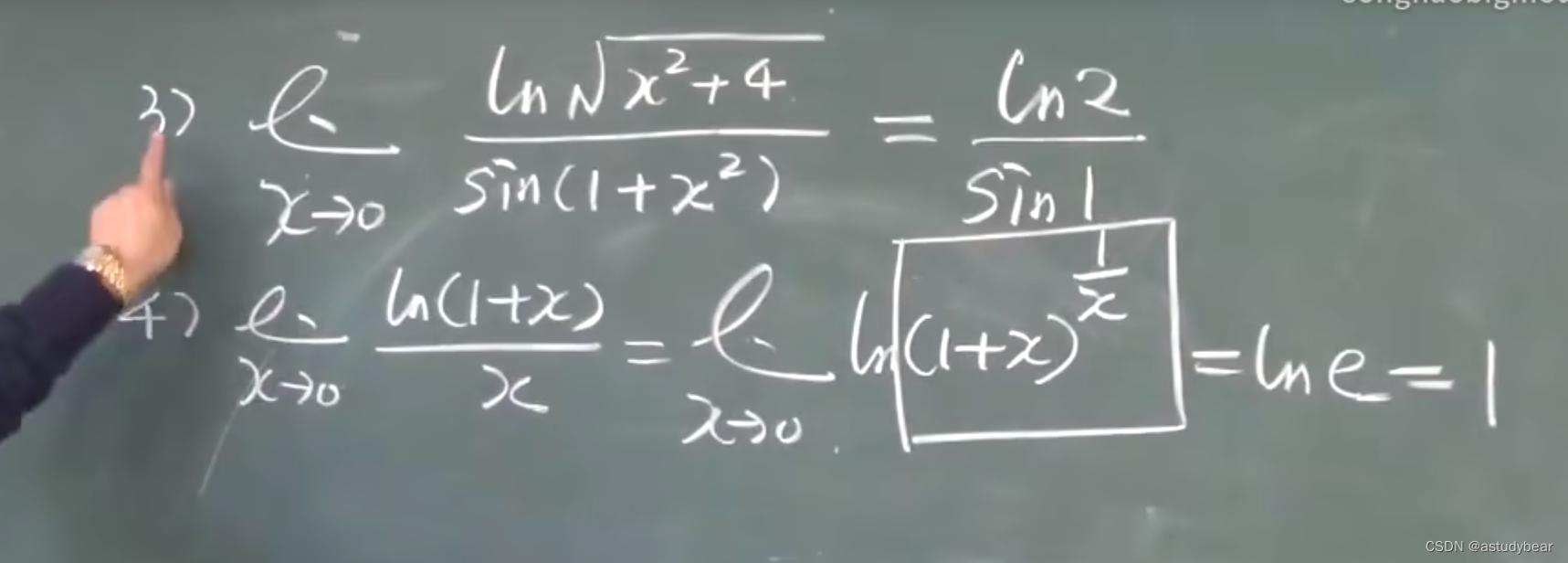
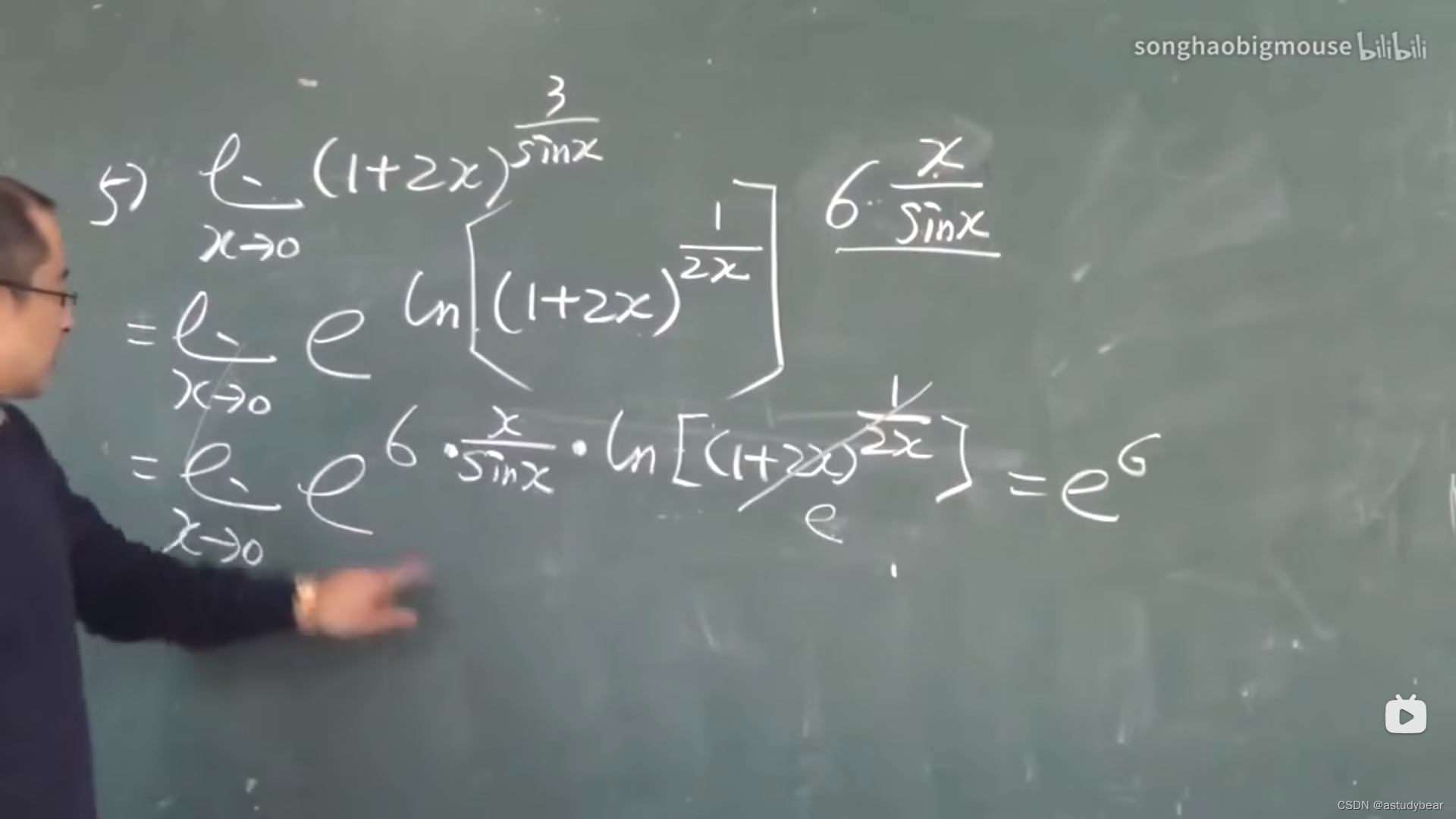
 一个公式的推导证明👇 

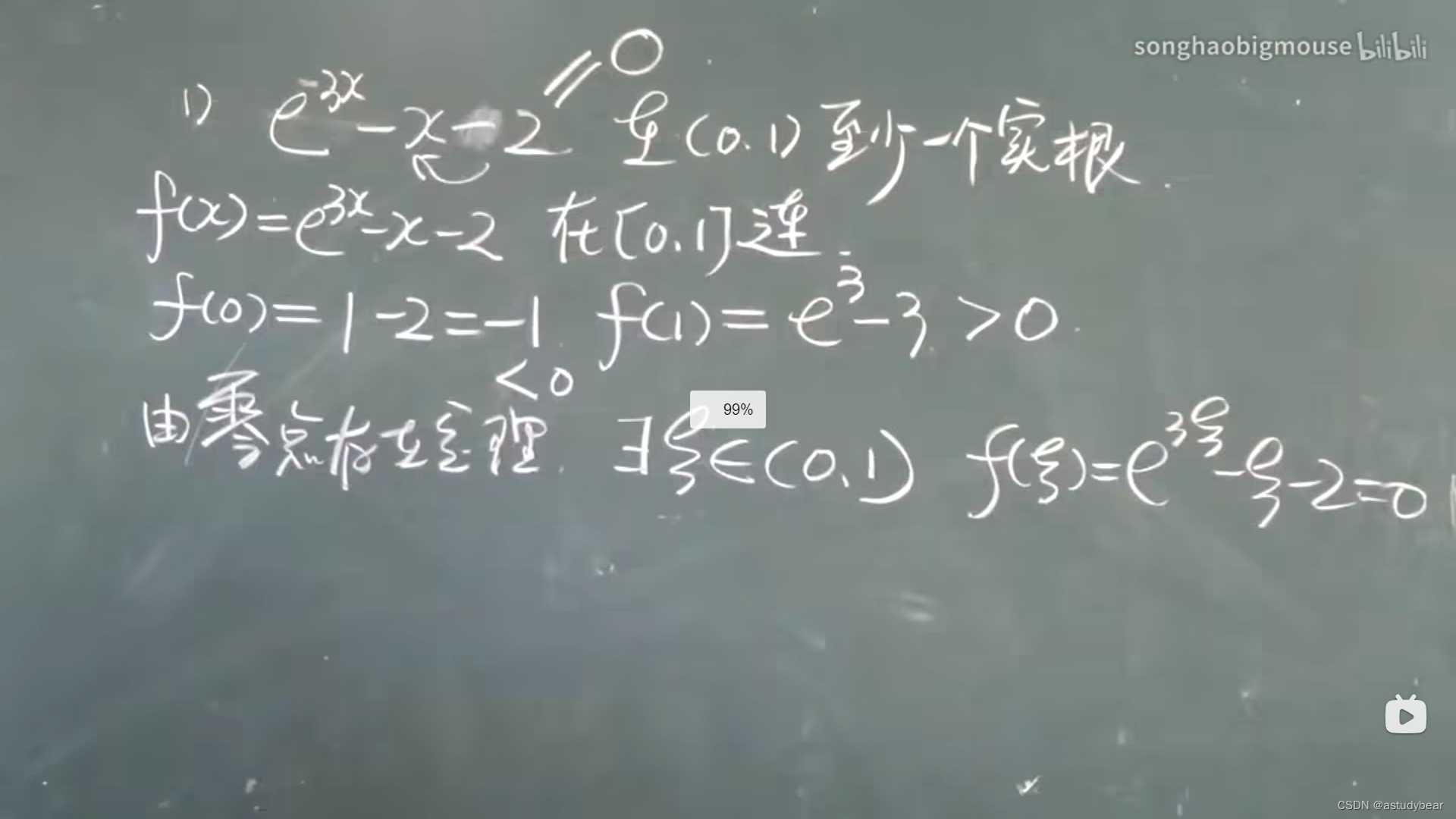
小结：

函数的连续这部分，比较重要的三种题型①零点存在定理②由连续性求复合函数的极限③已知连续求里面的参数的取值 

2.1导数的定义

 

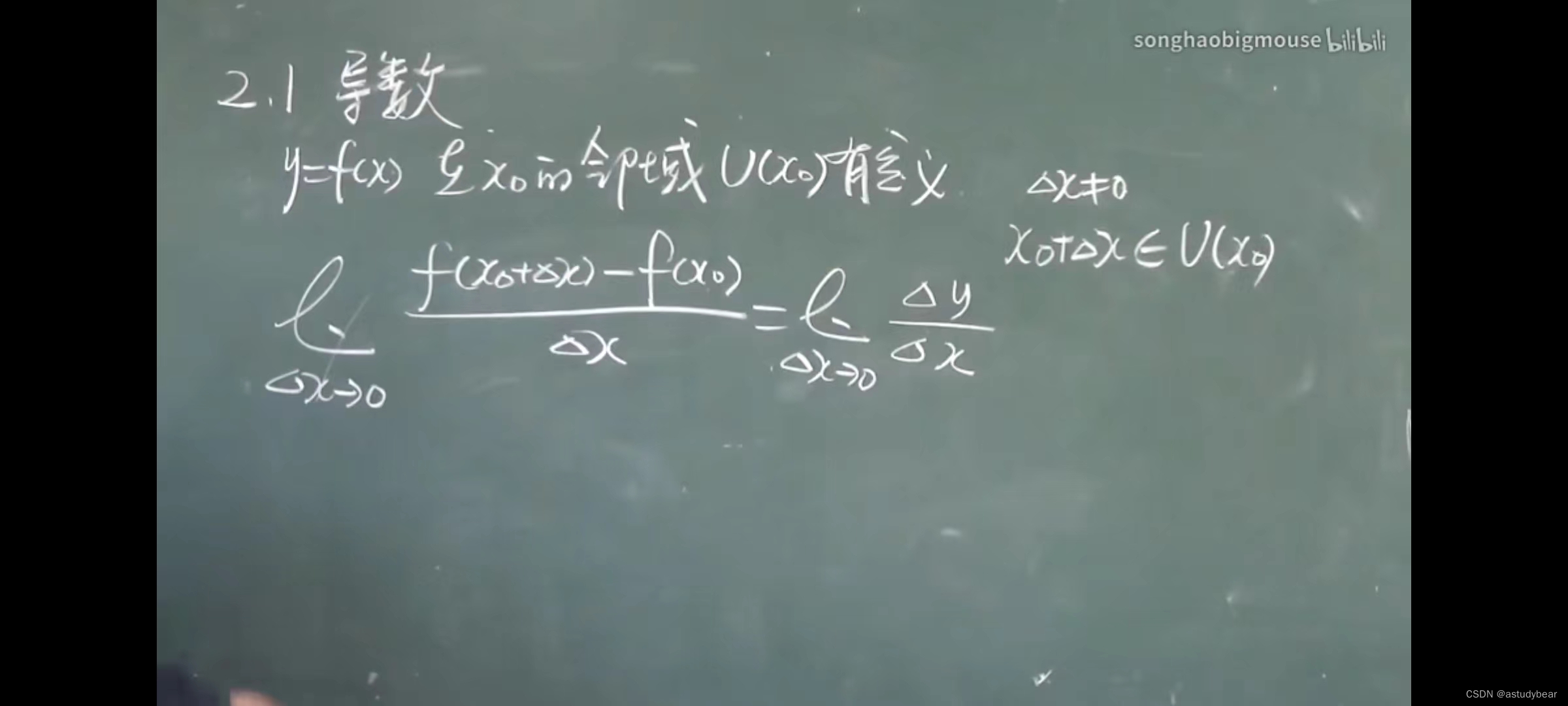
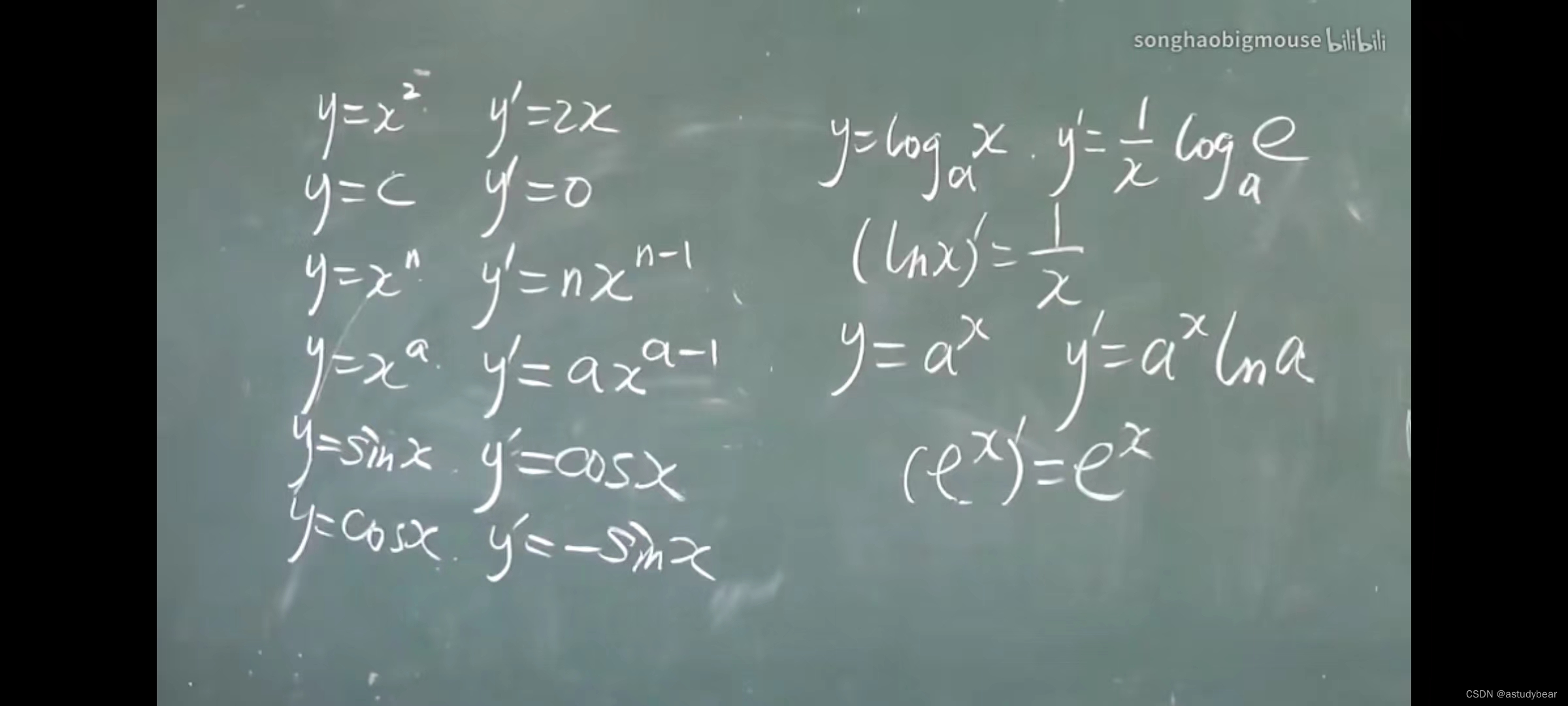
切线和法线

 

例题（求某点是否可导） 

判断在某点处是否可导就是求他的左右导数是否相等 

可导和连续的关系 （导数的定义比连续的定义强）

 例题：

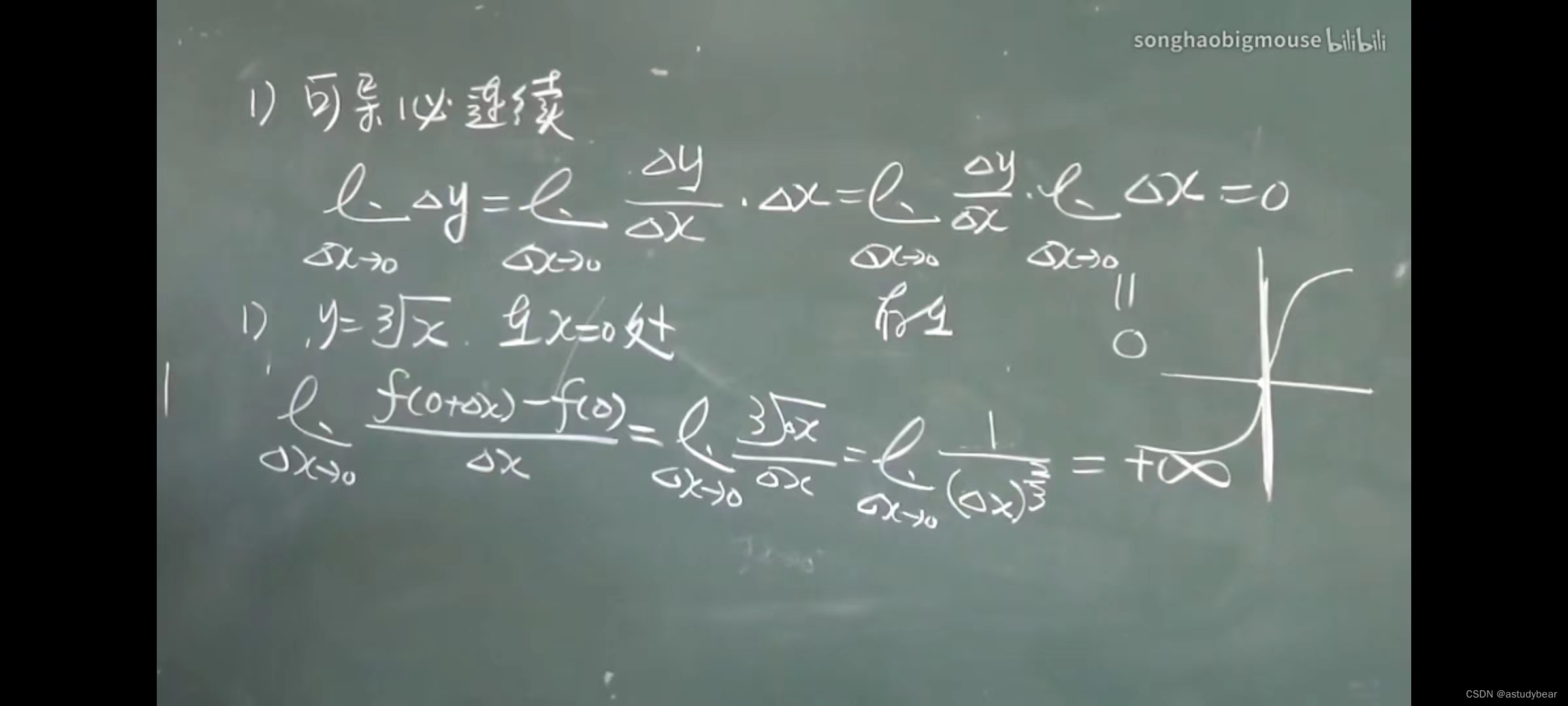
2.2求导法则

 

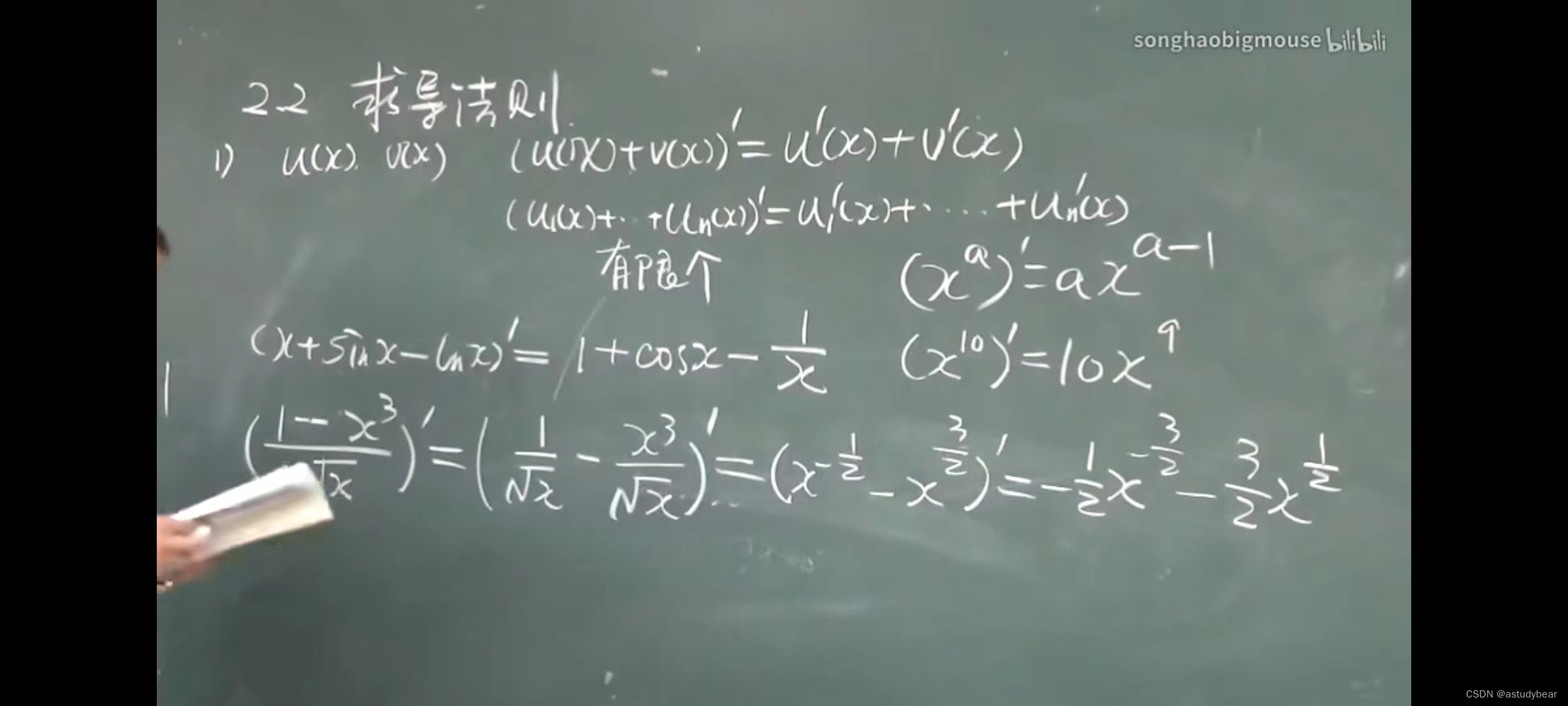
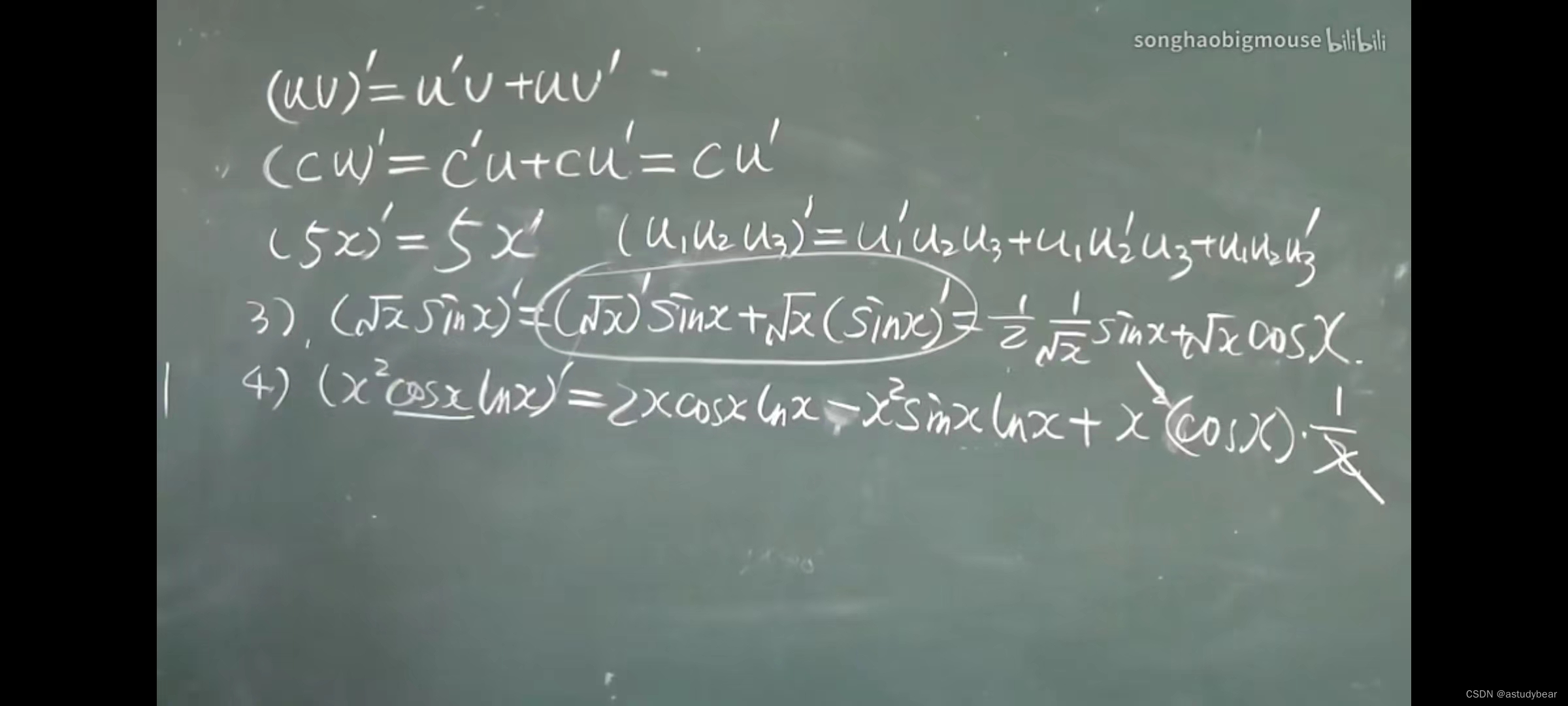
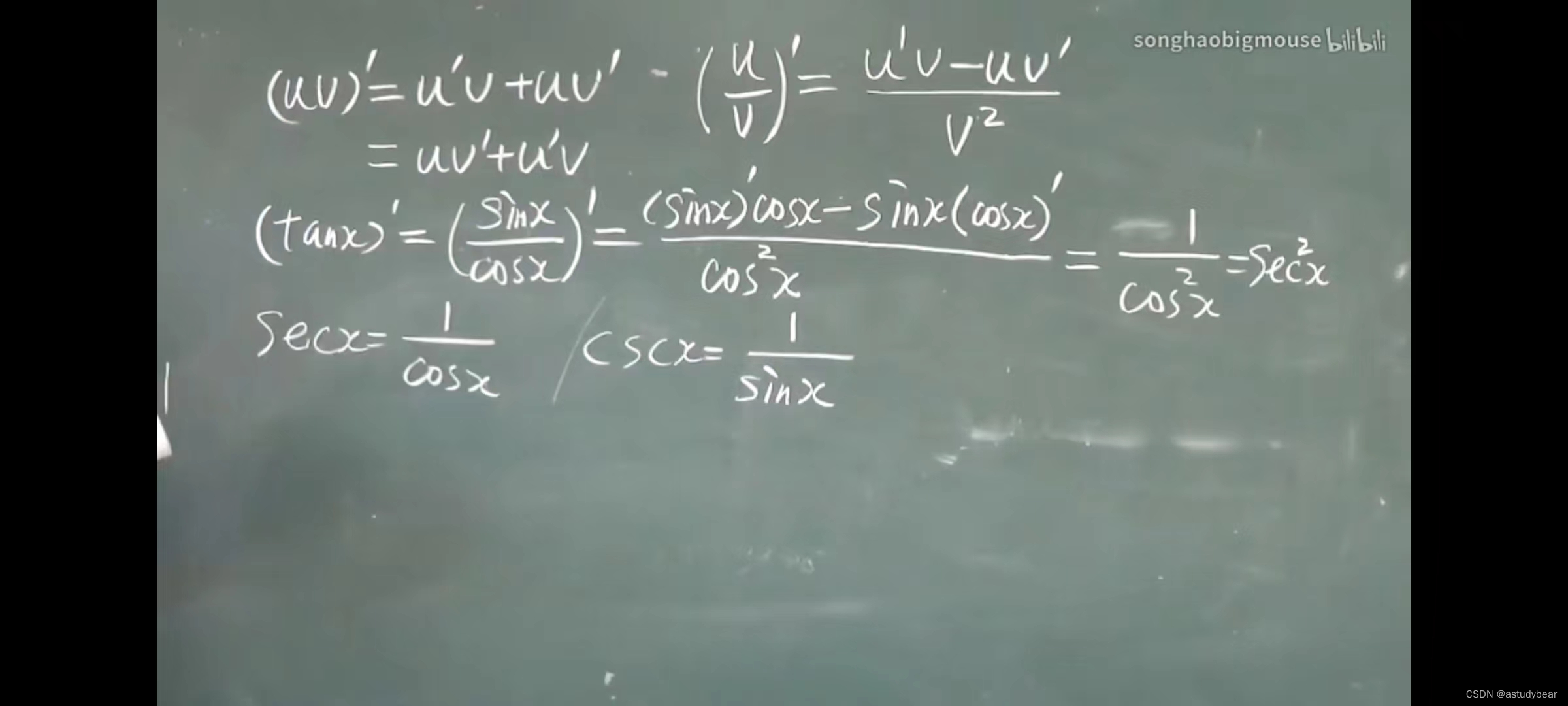
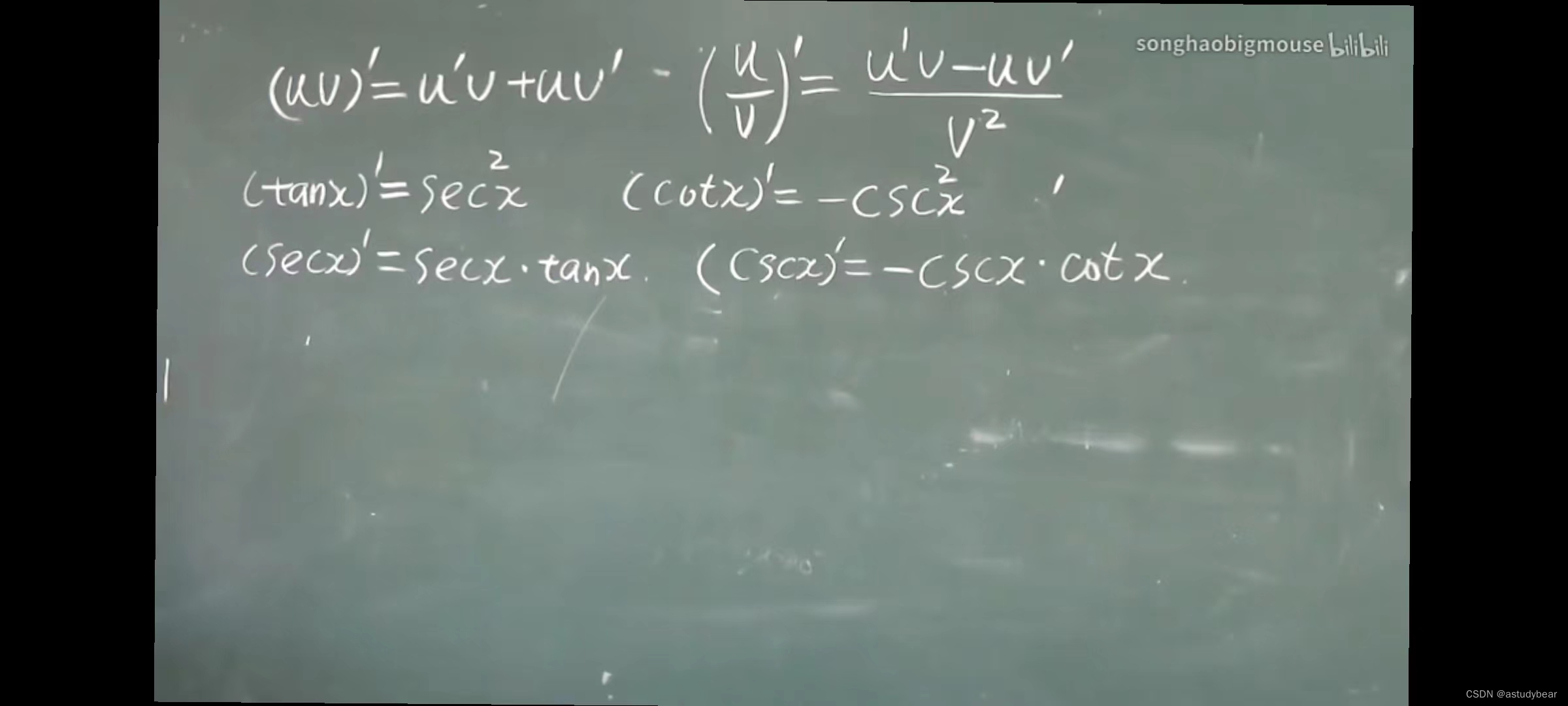
 利用反函数求导（导数等于反函数的倒数）

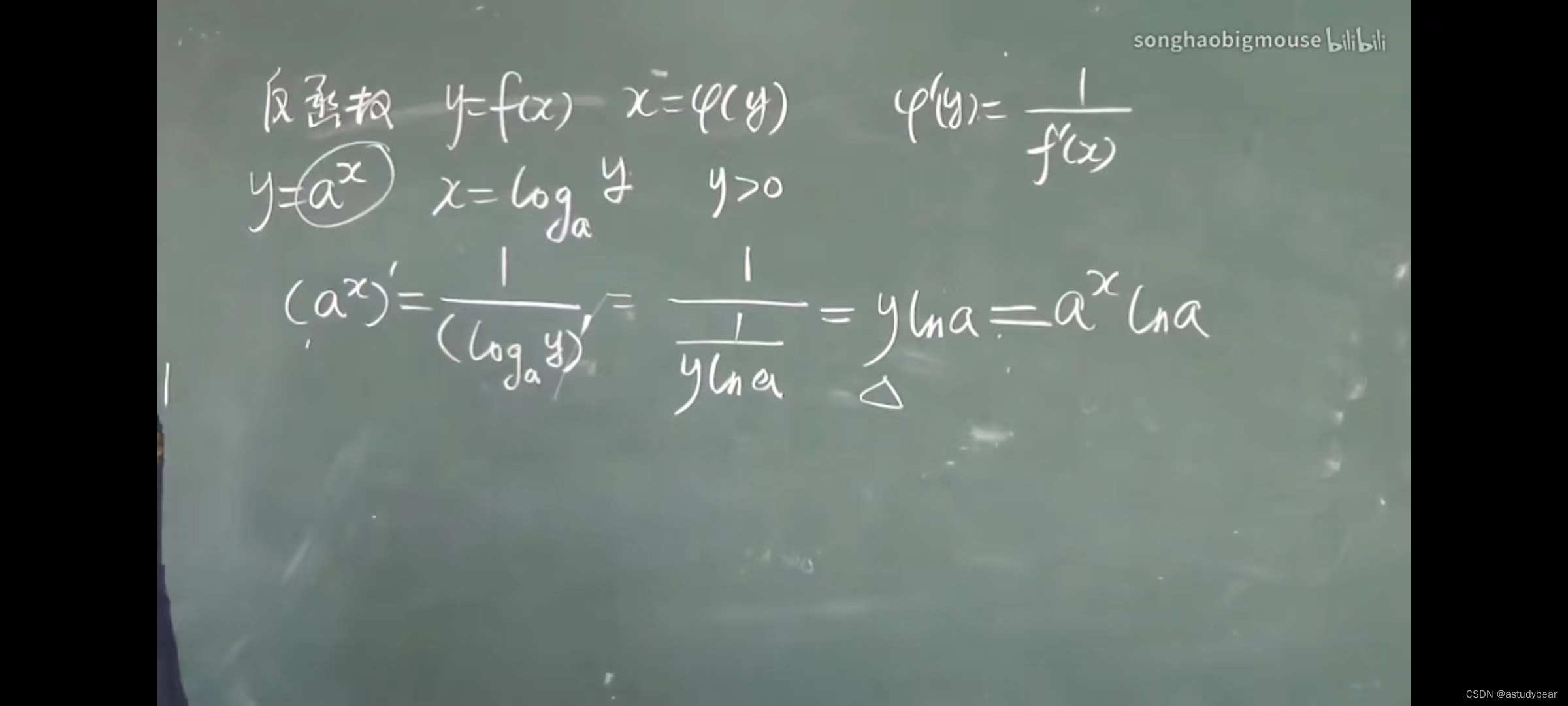
 结论

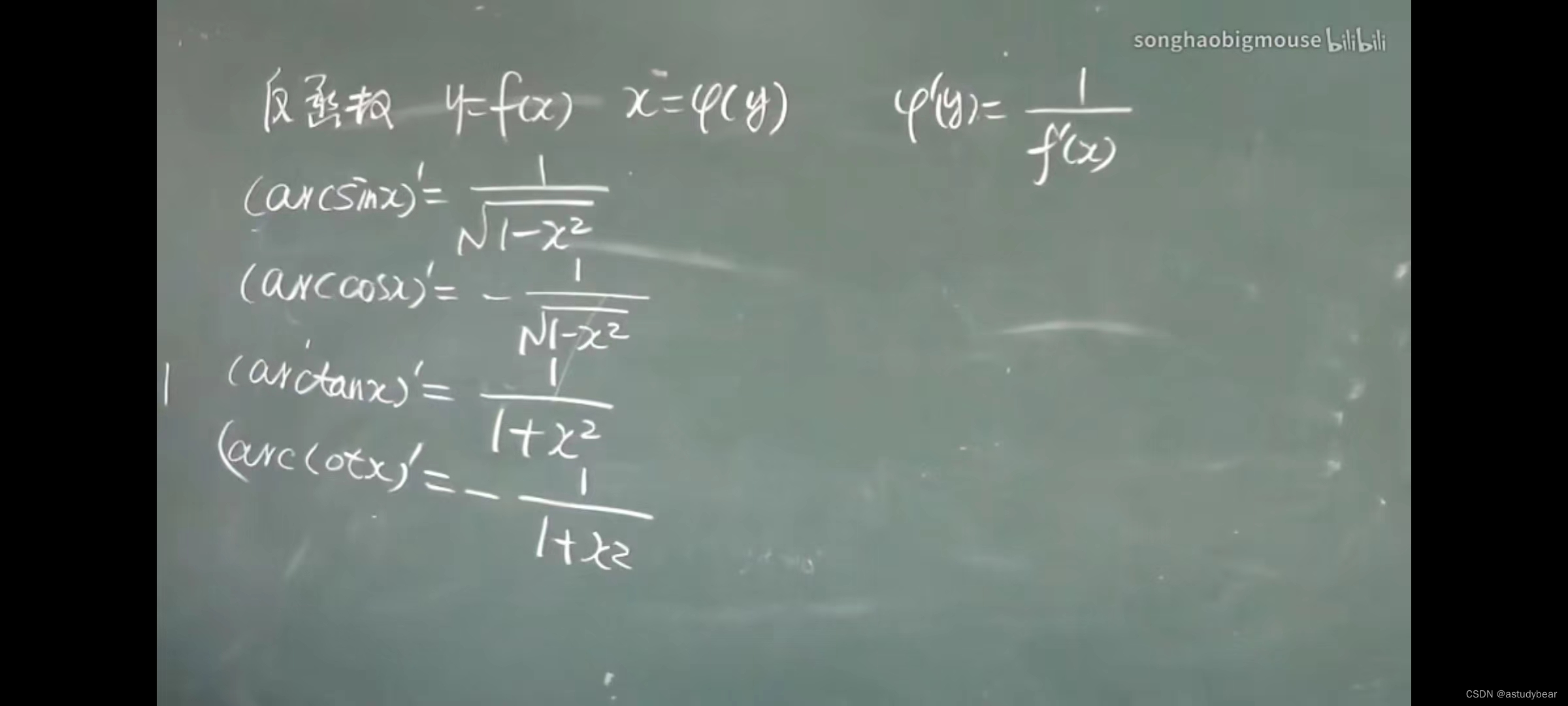
 复合函数的链式法则

 复合求导法则的拨洋葱

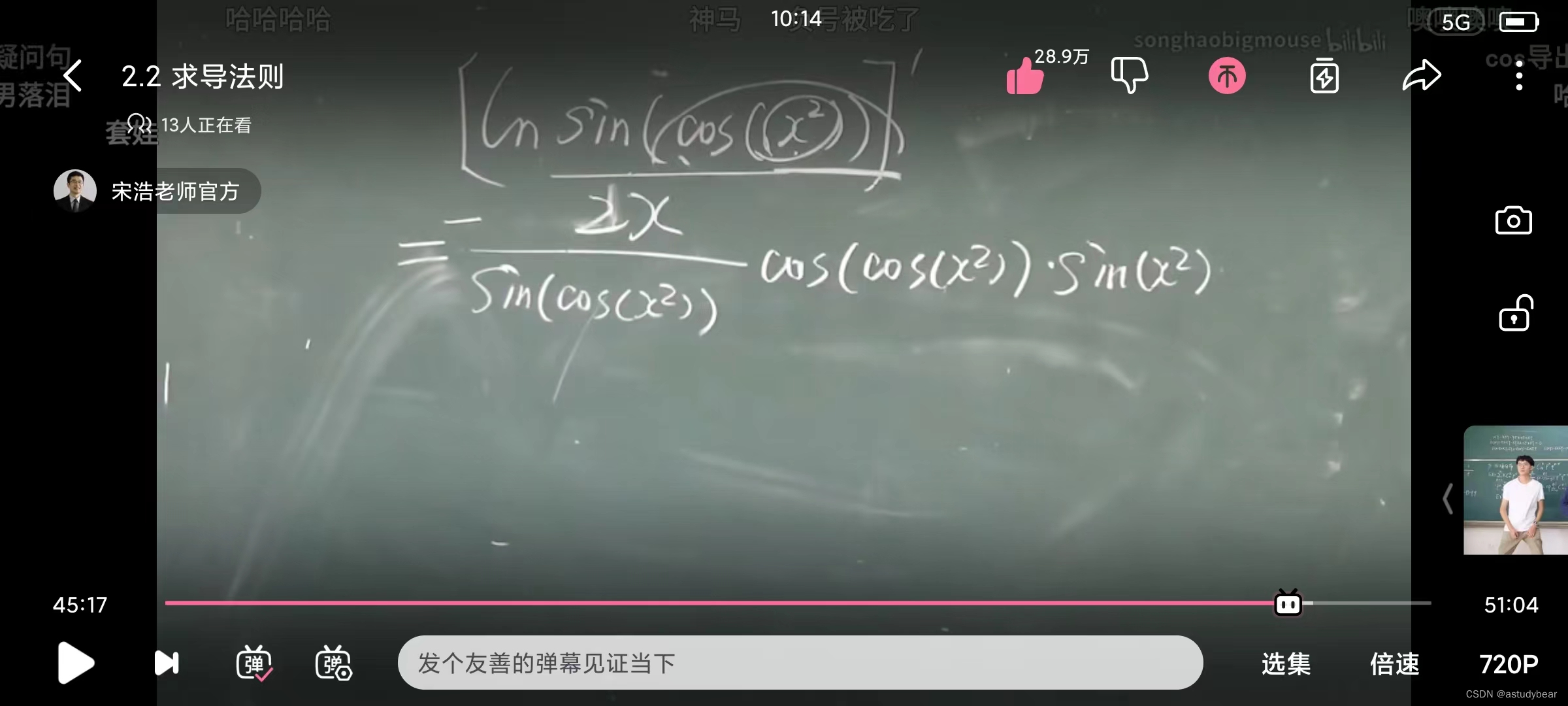
 例题

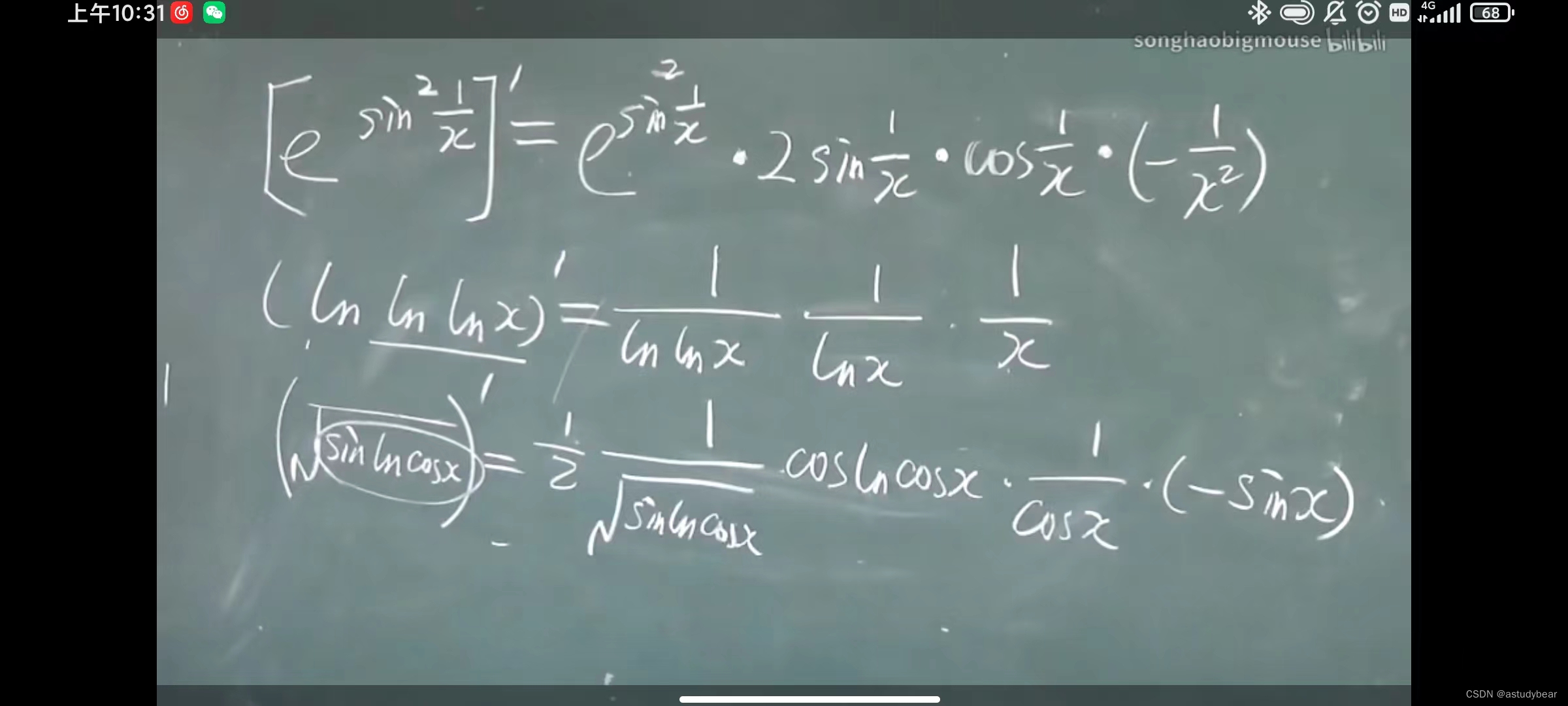
2.5微分

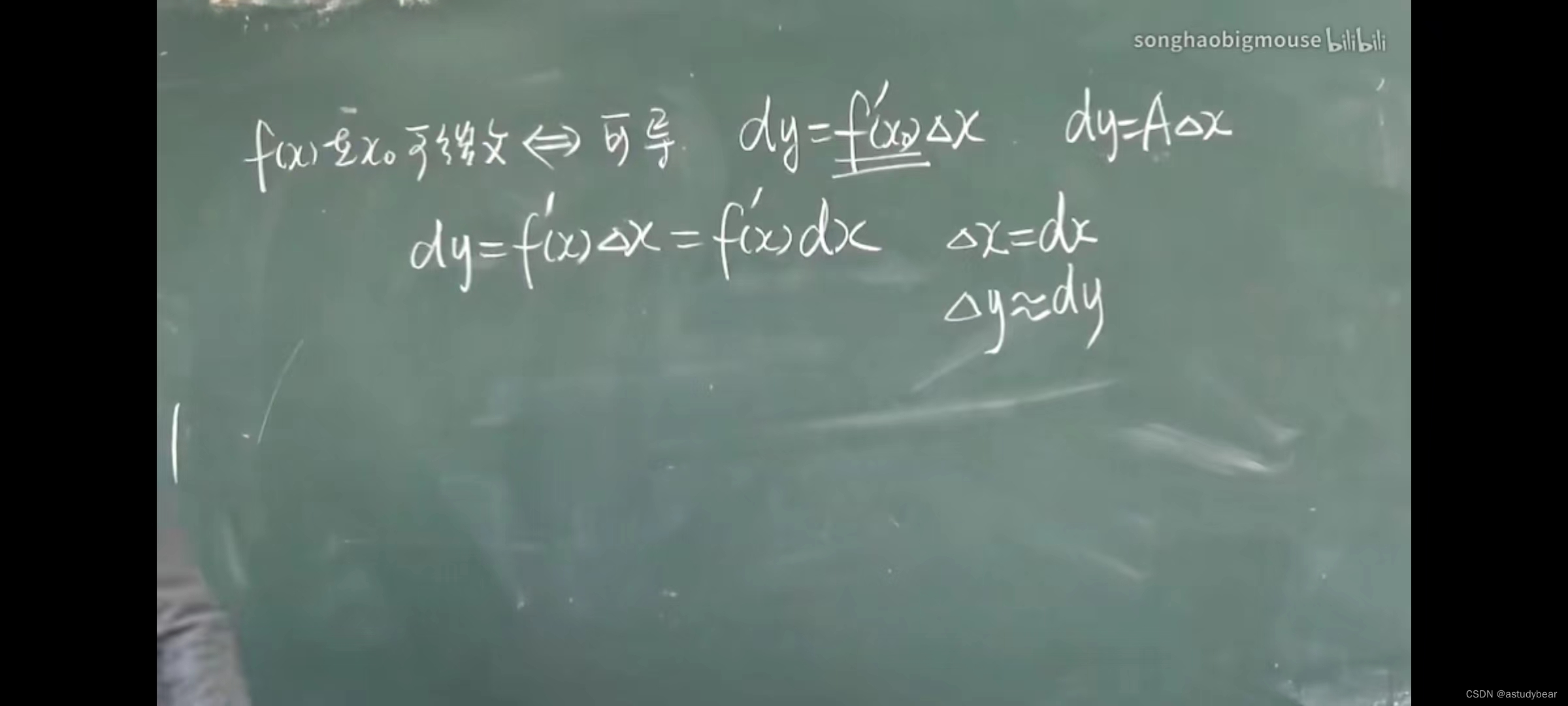
 例题

 图形理解

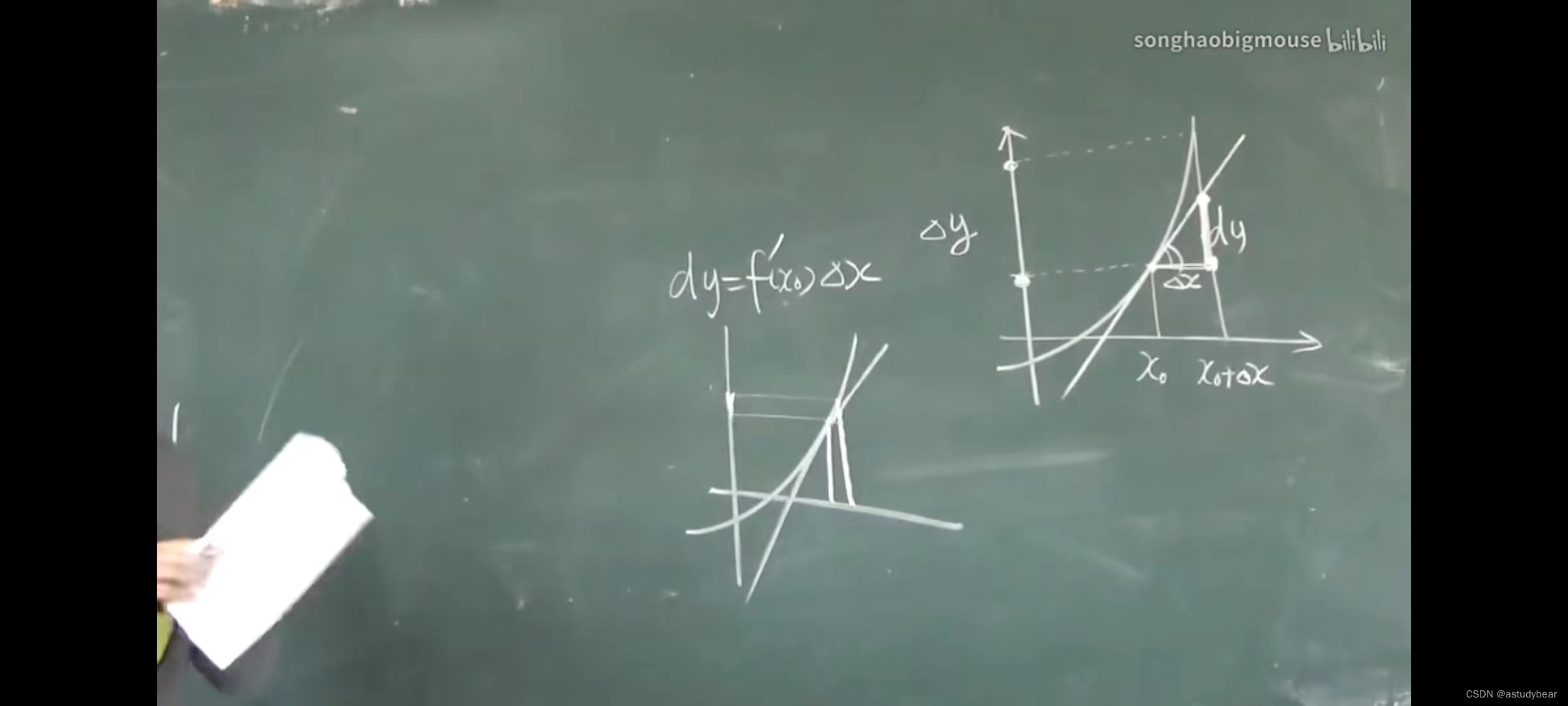
 微分四则运算

 例题一

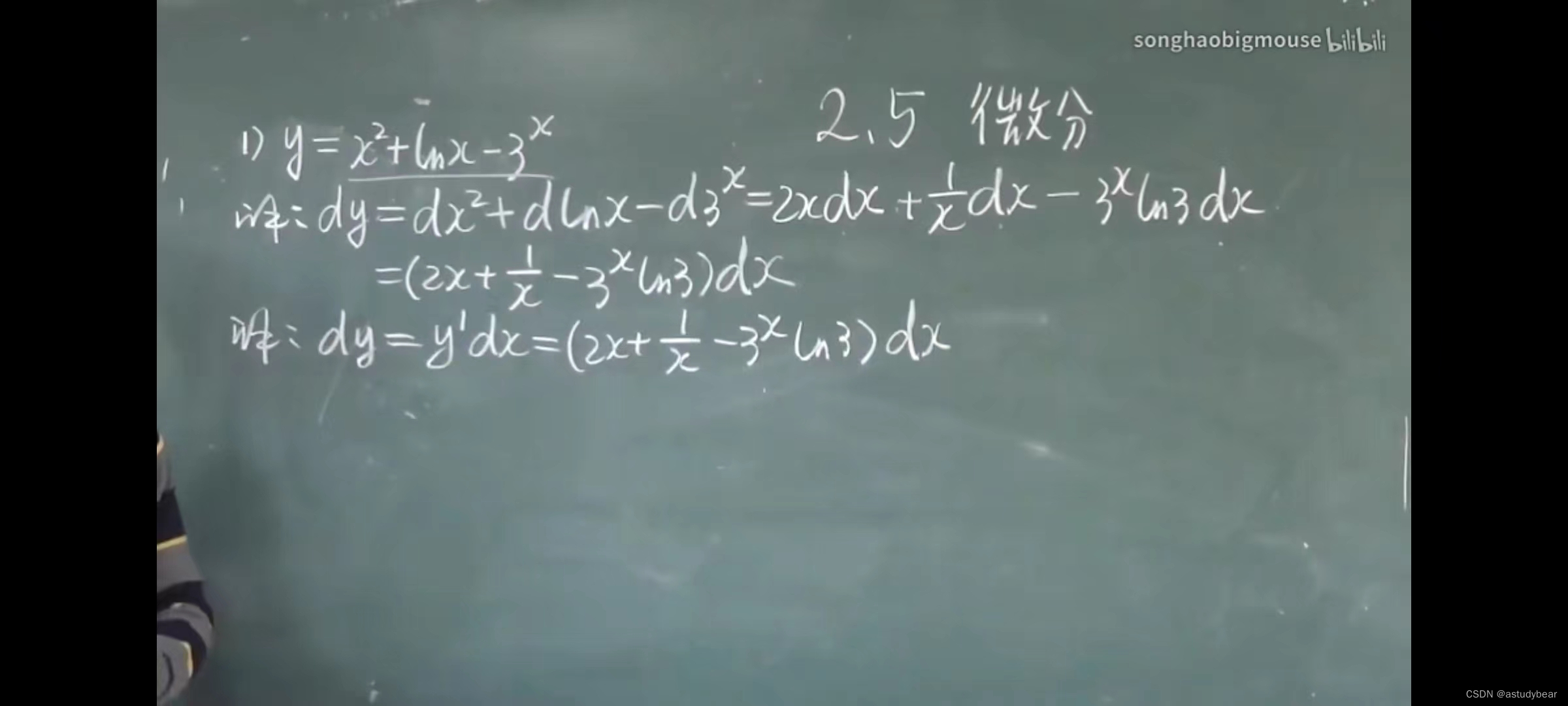
 小技巧，分子次数比分母高或相同的时候可以凑一下然后化简

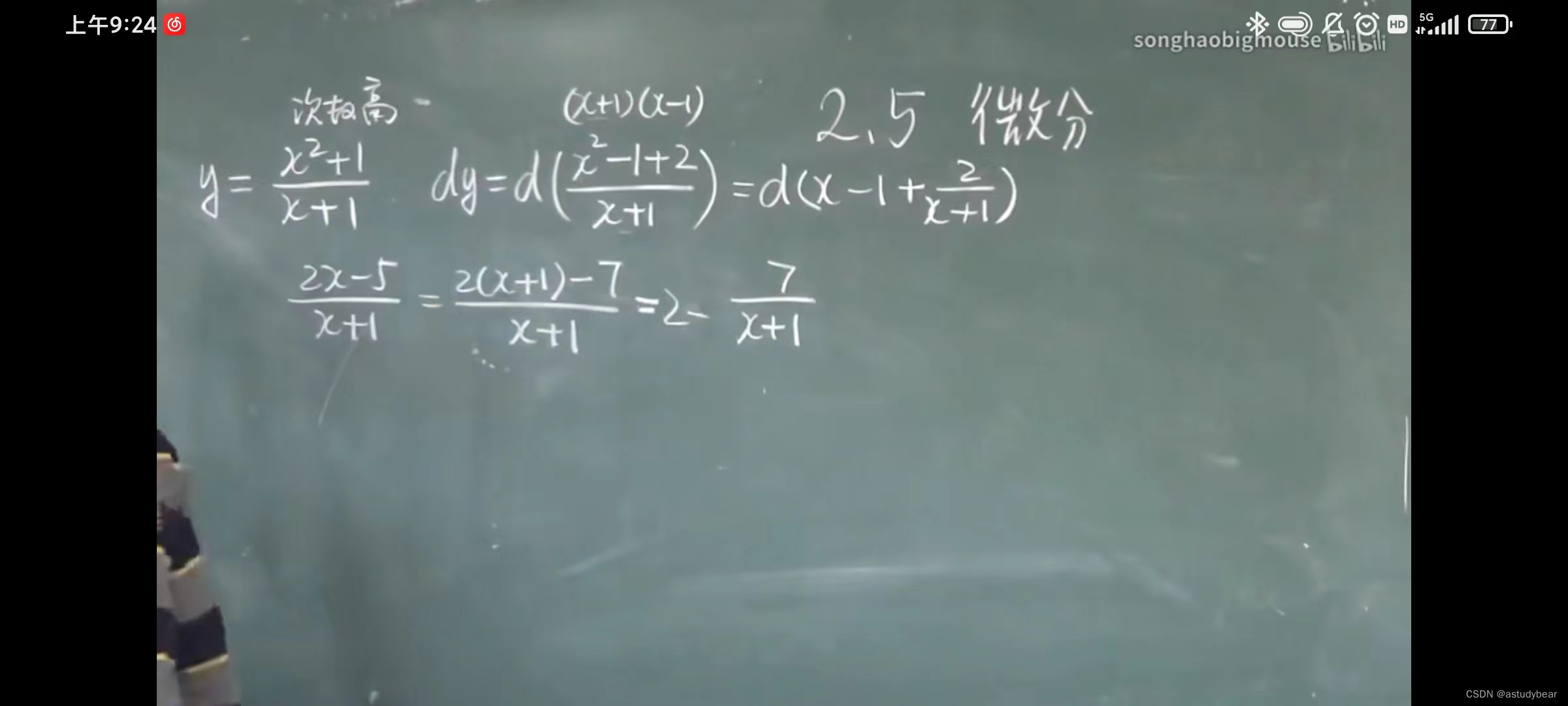
 例题二

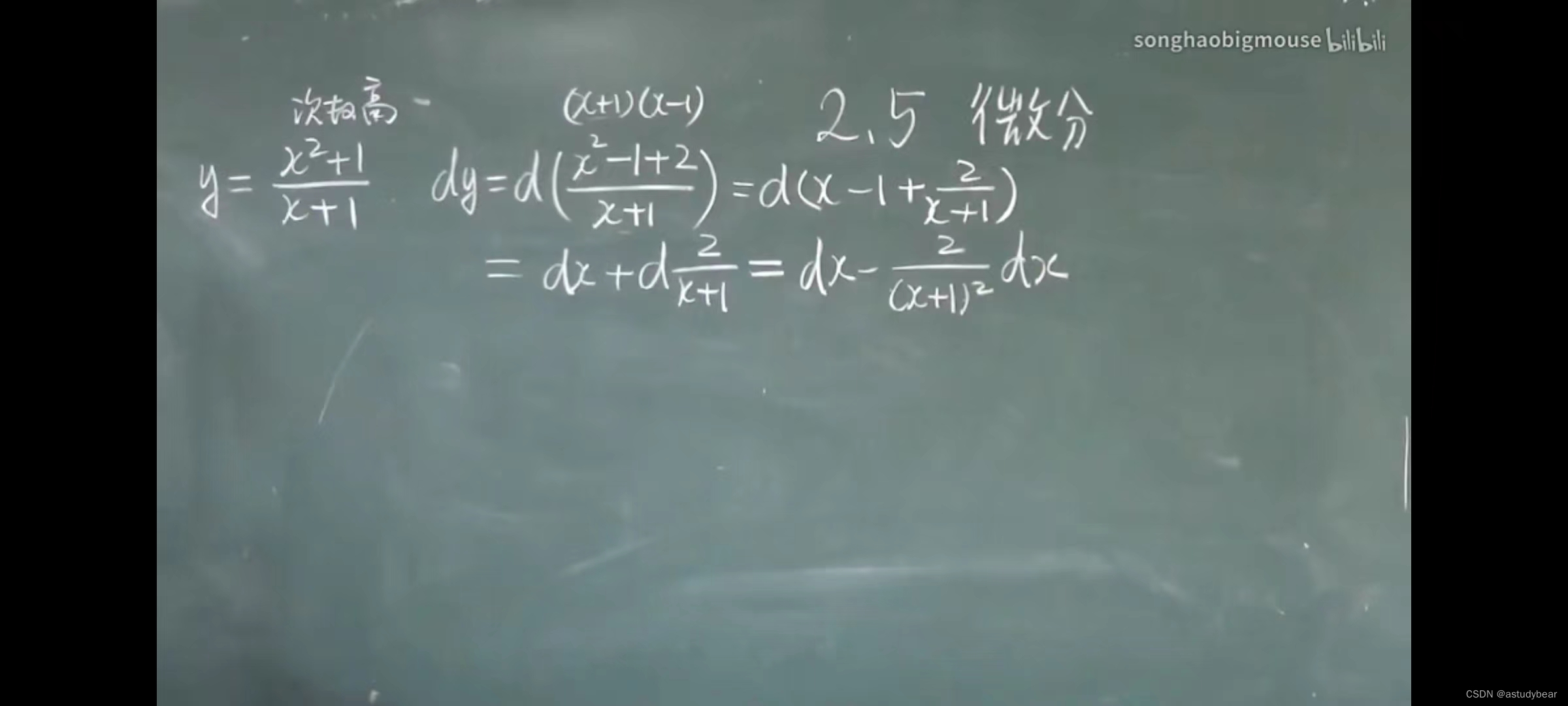
 一个概念:一阶微分形势不变性（基本没啥用，了解）

不管u是函数还是变量，他最后的形式都是不变的

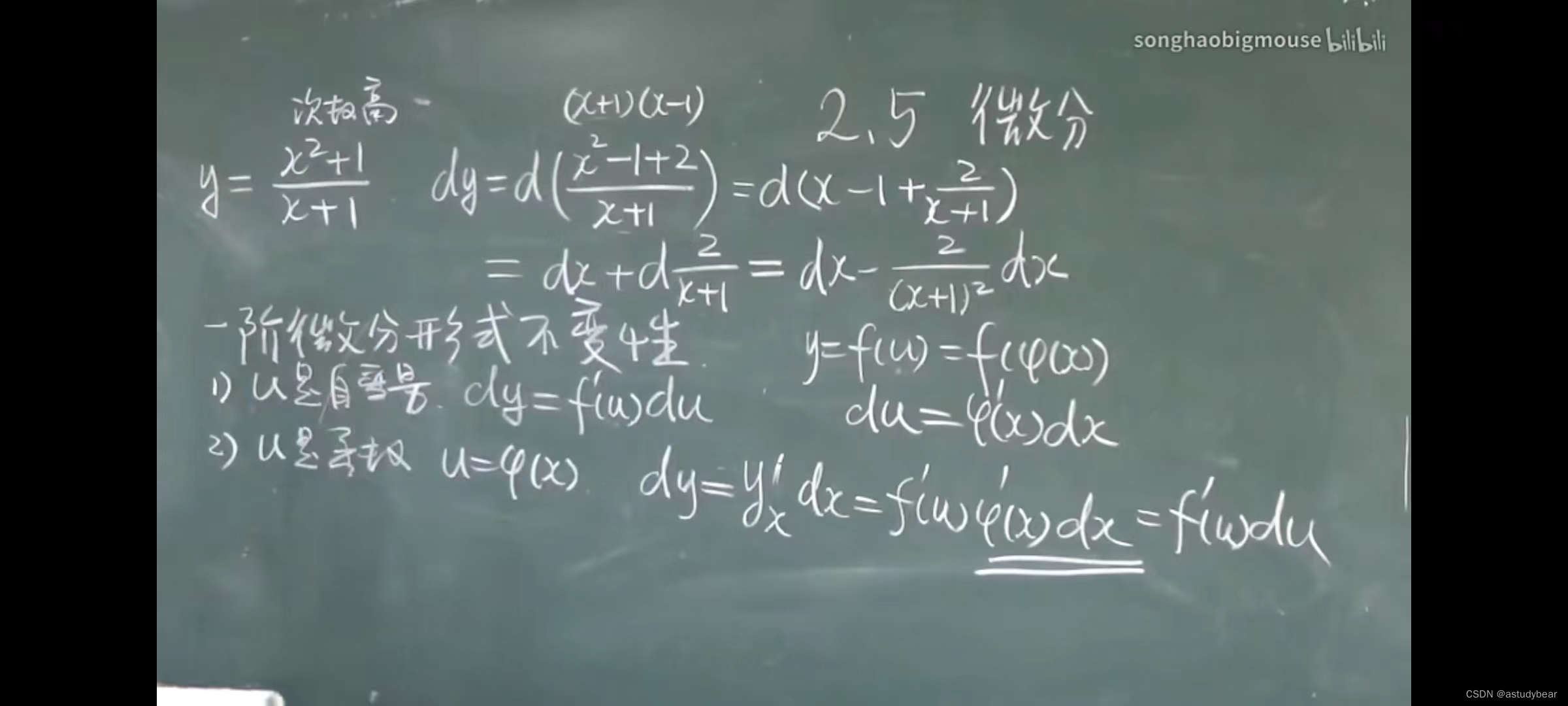
 例题

 

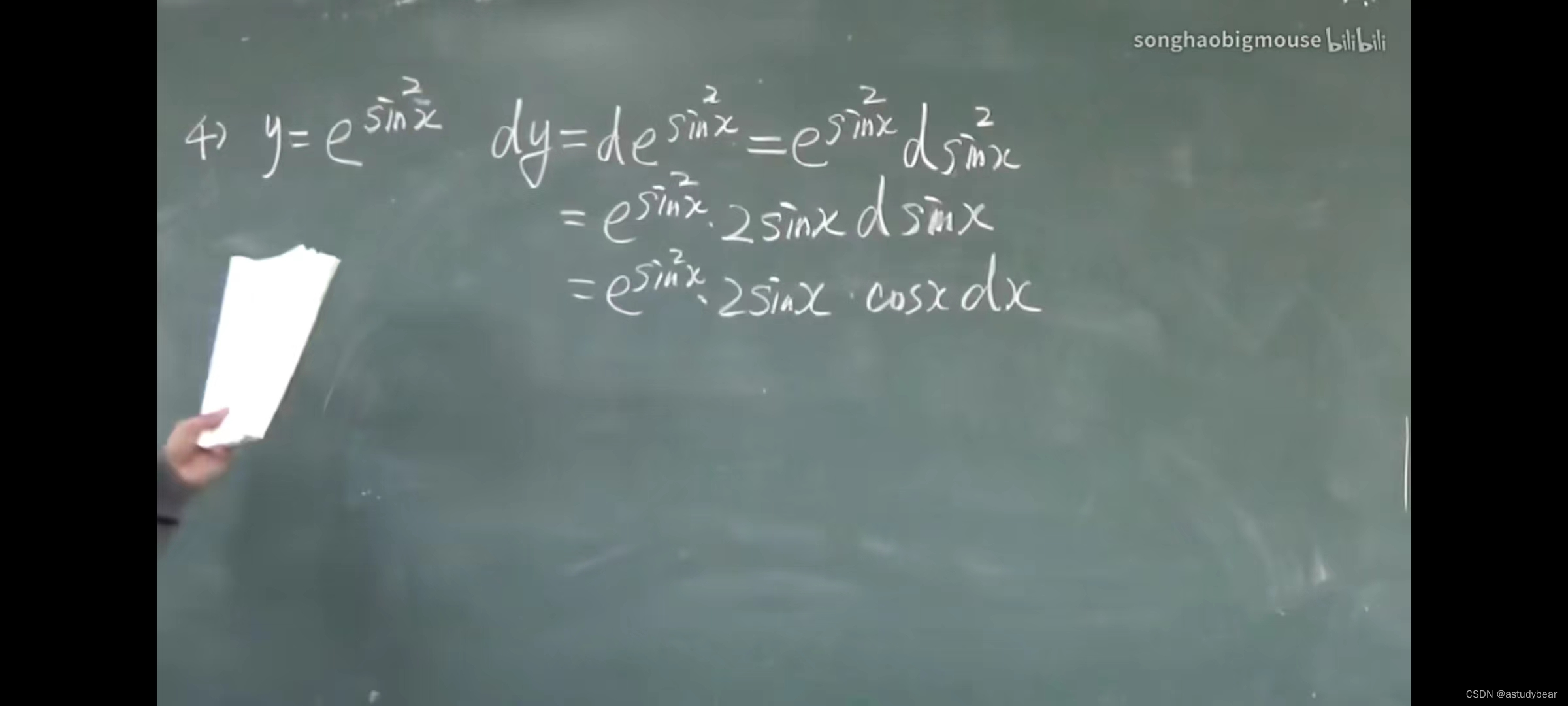
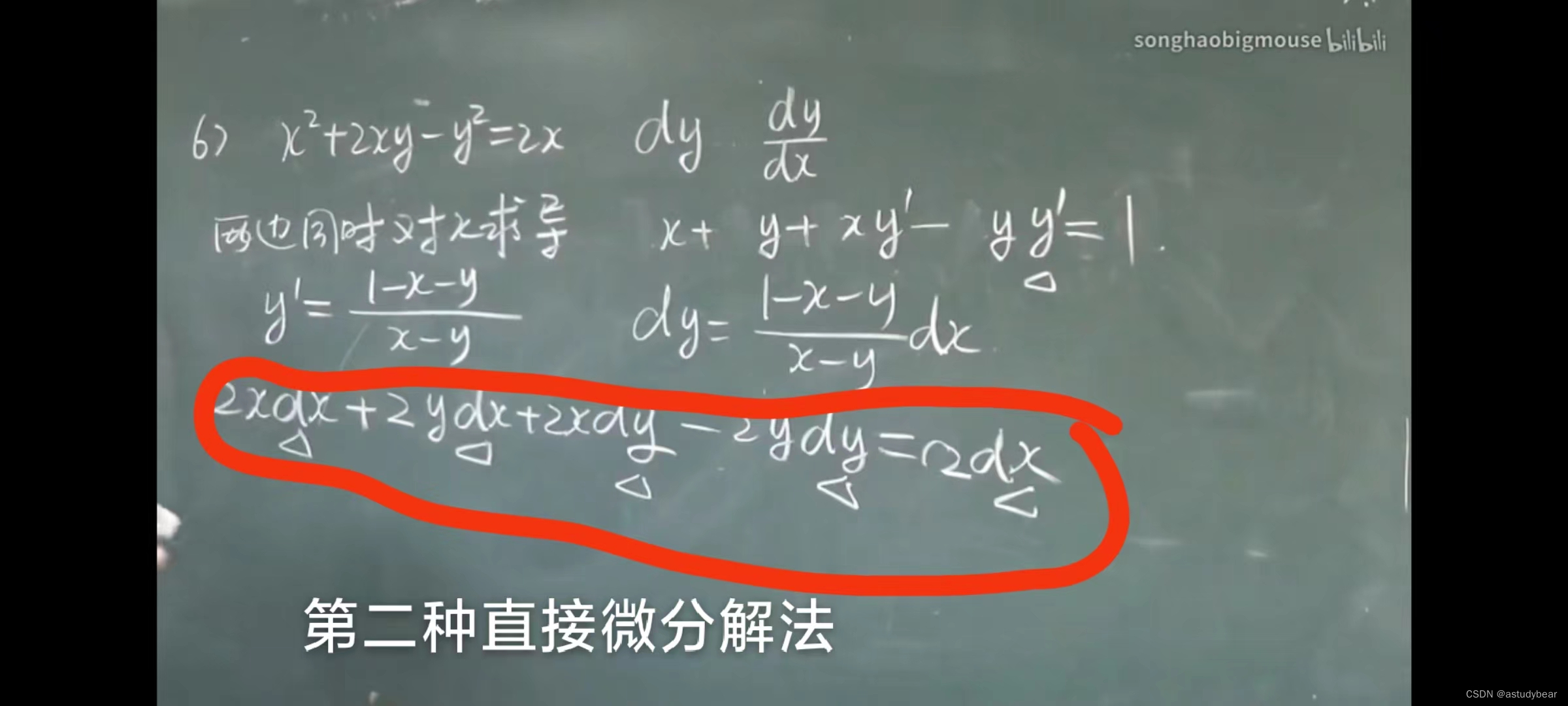
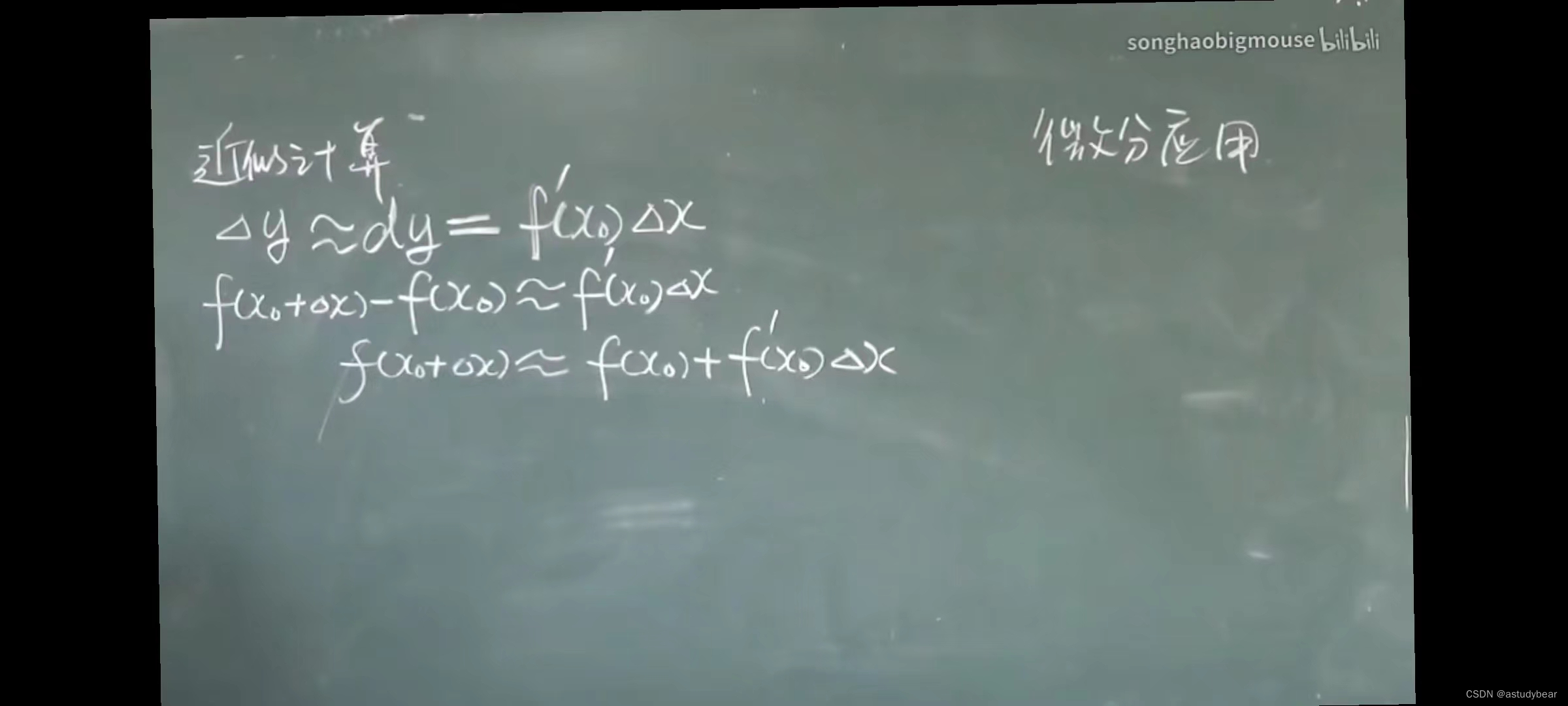 例题一

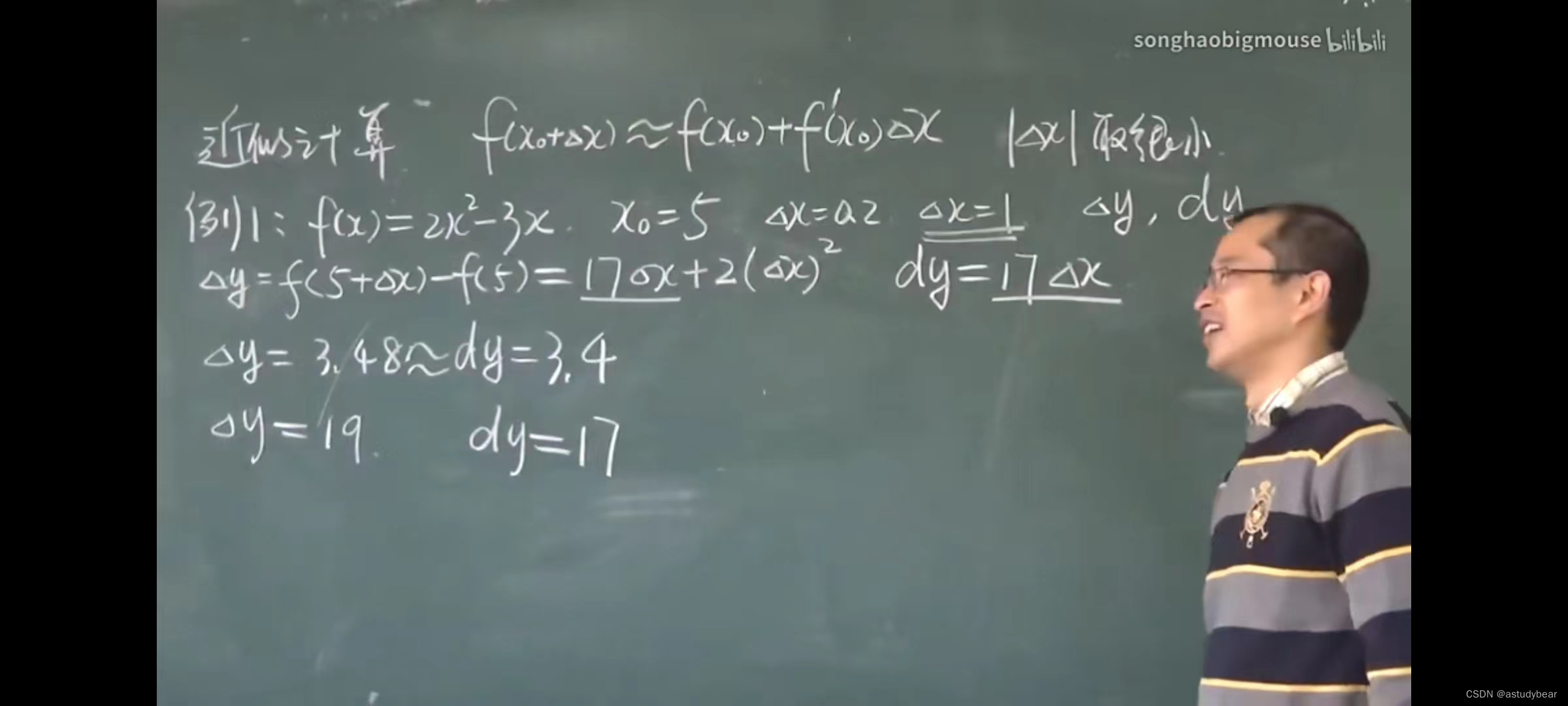
 由近视计算推导出来的八个公式

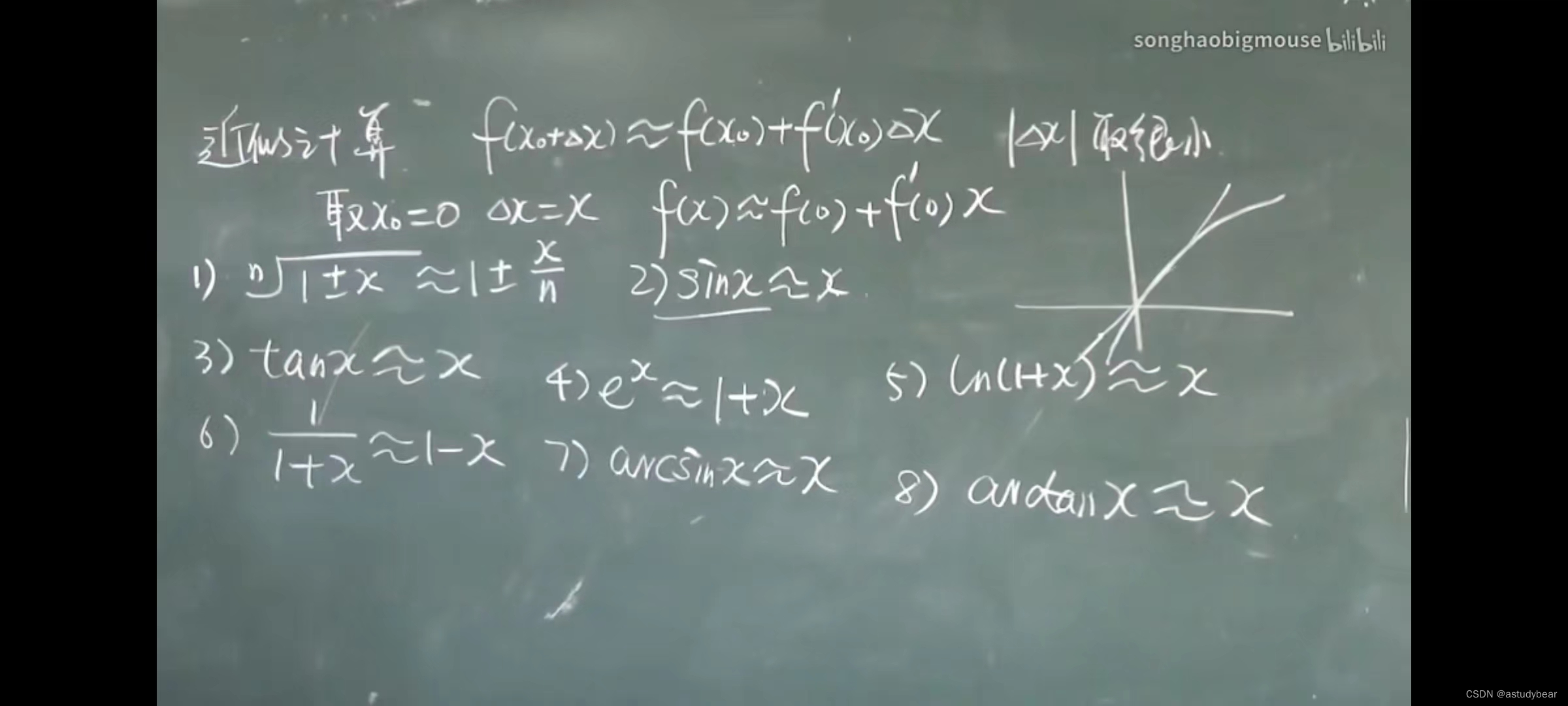
 例题二

 3.1微分中值定理

费马引理

罗尔定理

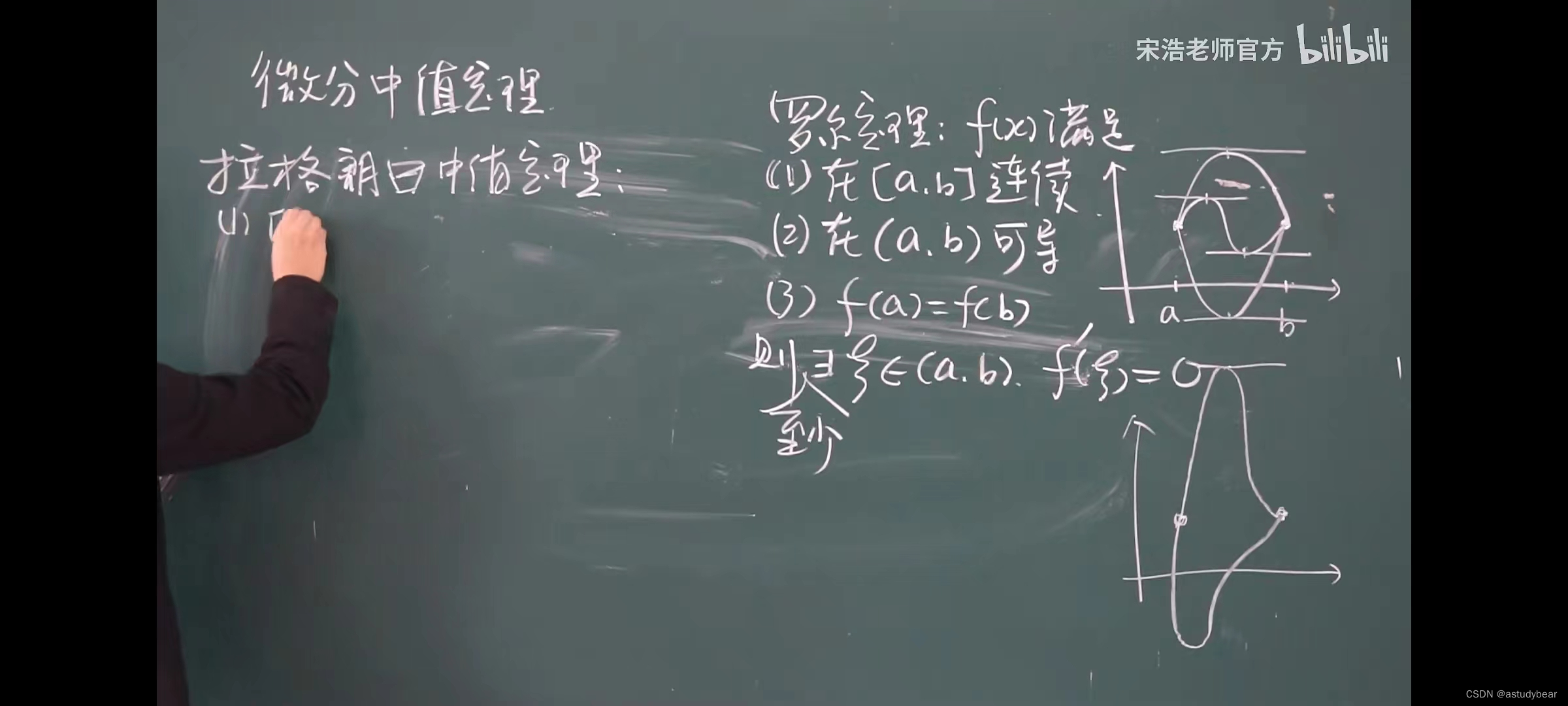 拉格郎日中定理

 

 推导定理

柯西中值定理

 两个函数要在同一个点

3.2洛必达法则

证明：

 结论：

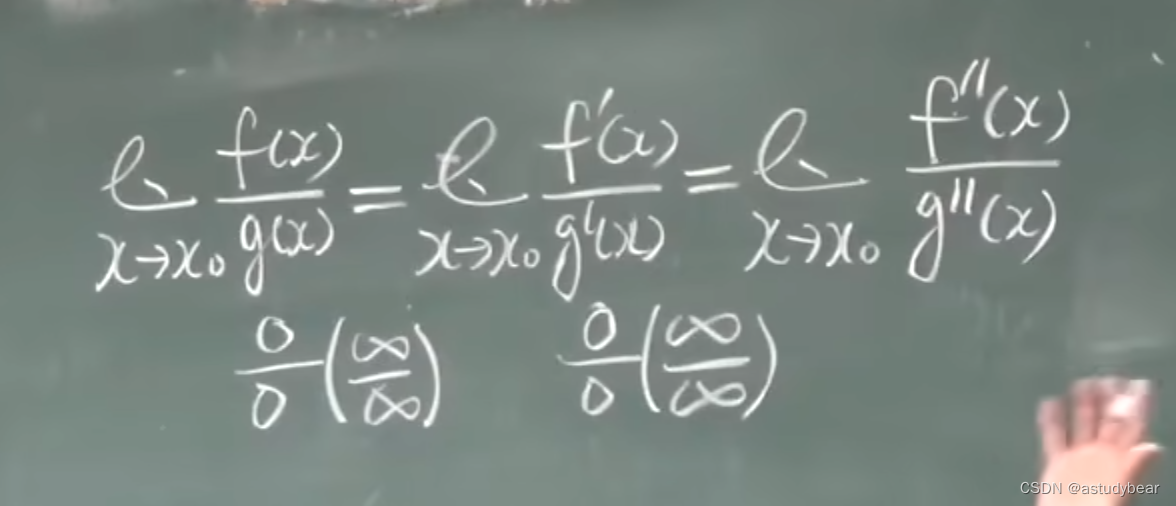
 例题：

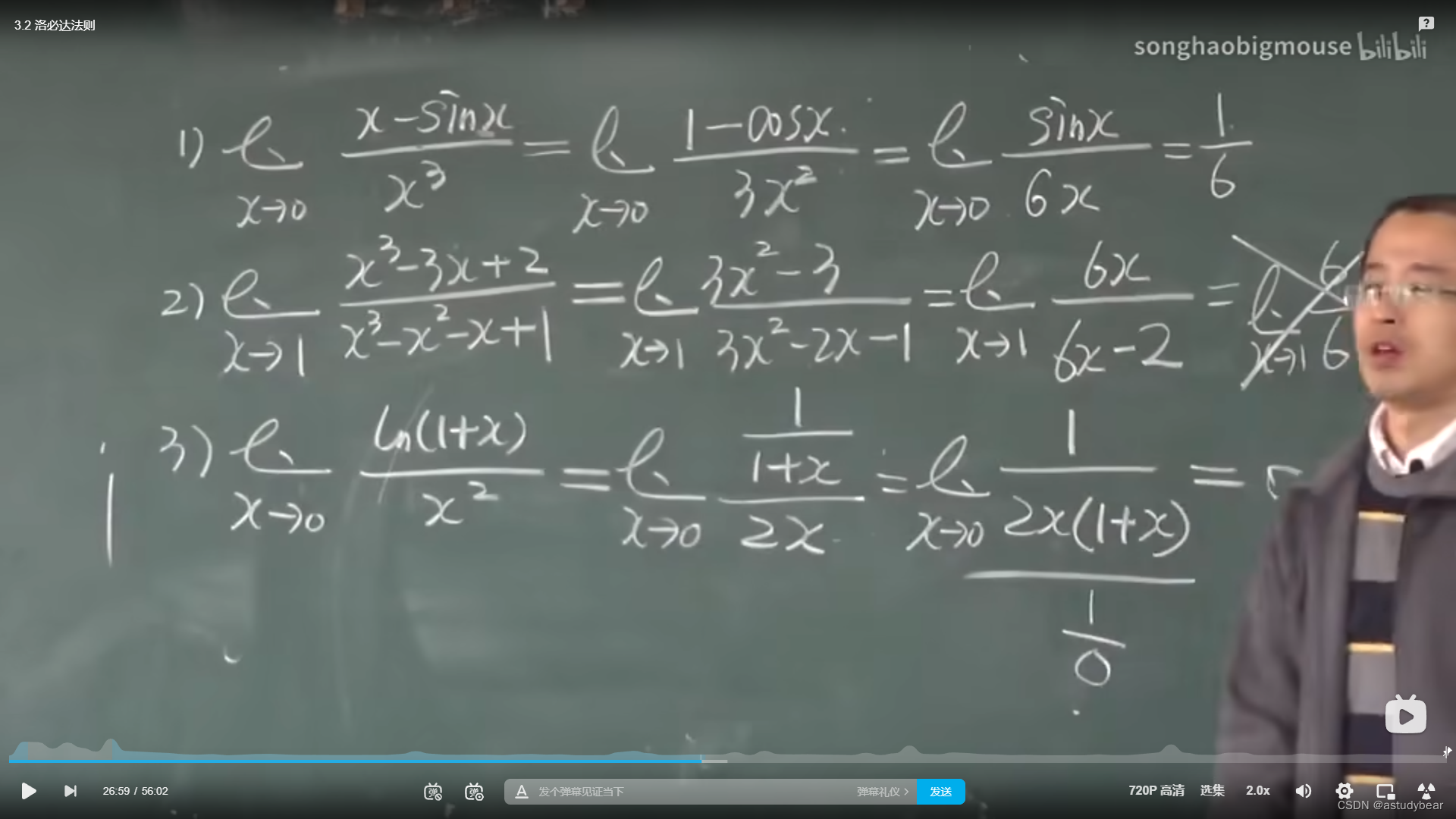
 必须是上下比是0/0或者无穷/无穷才能用

 例题

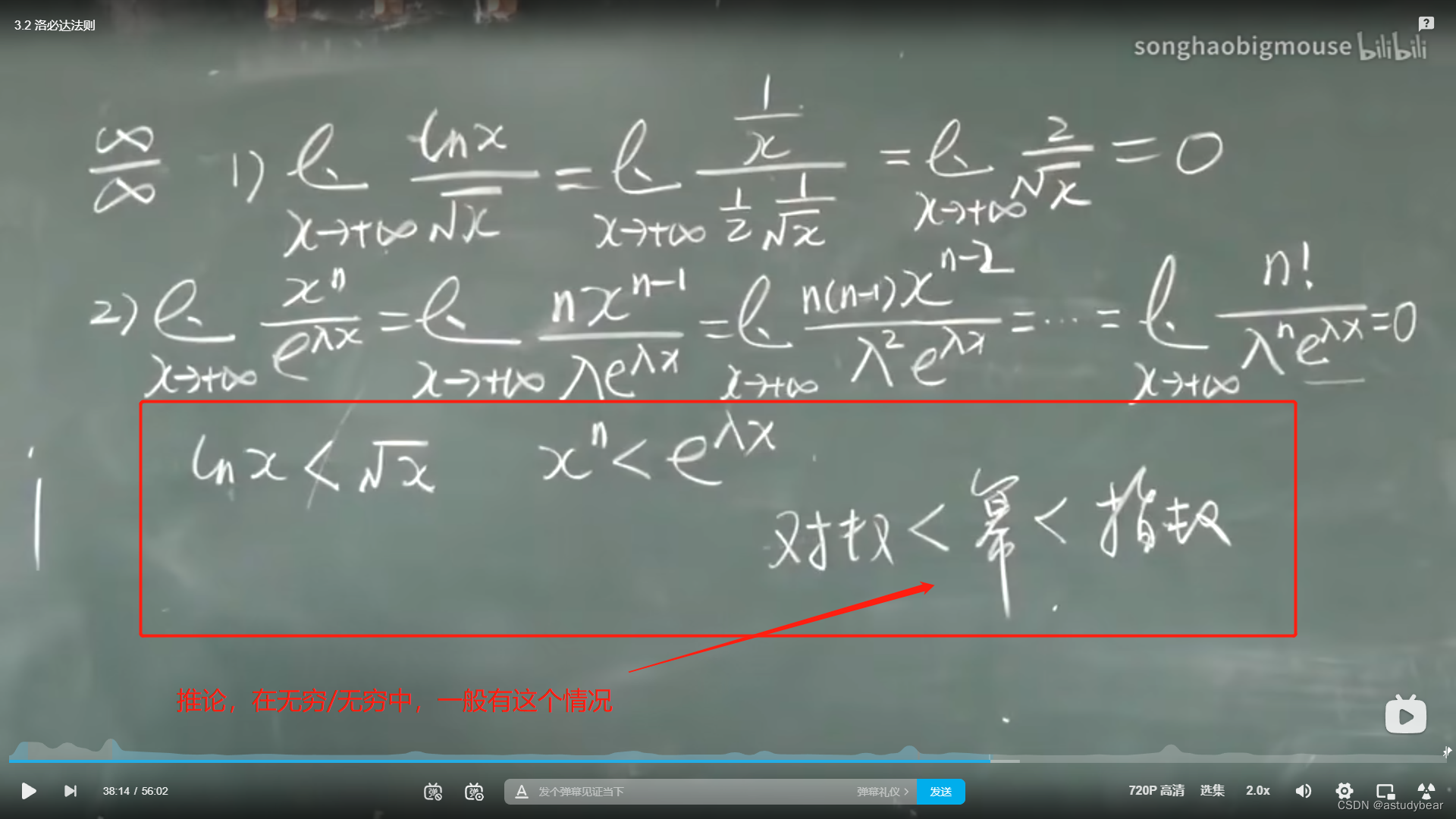
总结

 例题

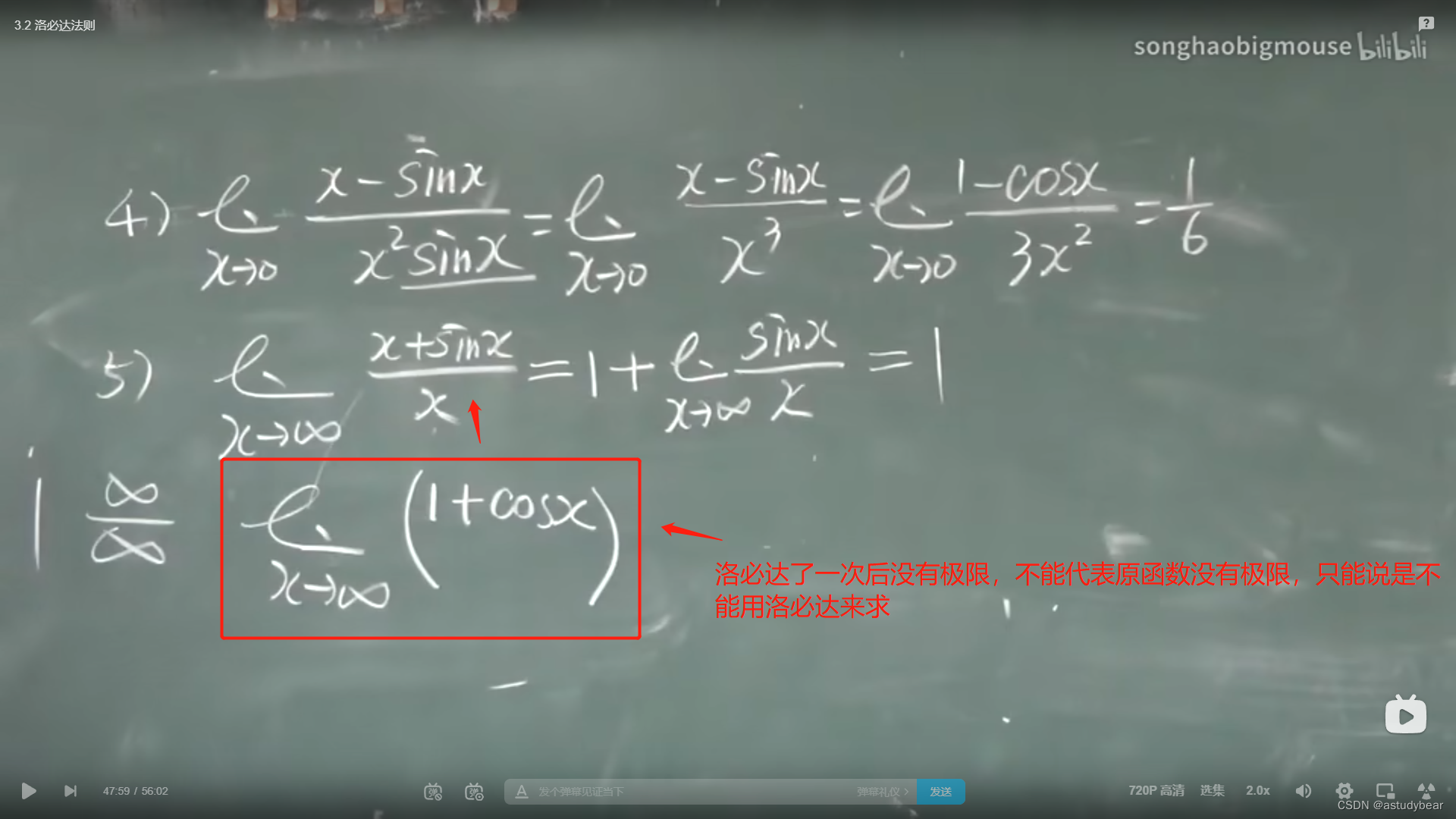
 洛必达适用的情况：（后面的必须转化成前面的才能用） 

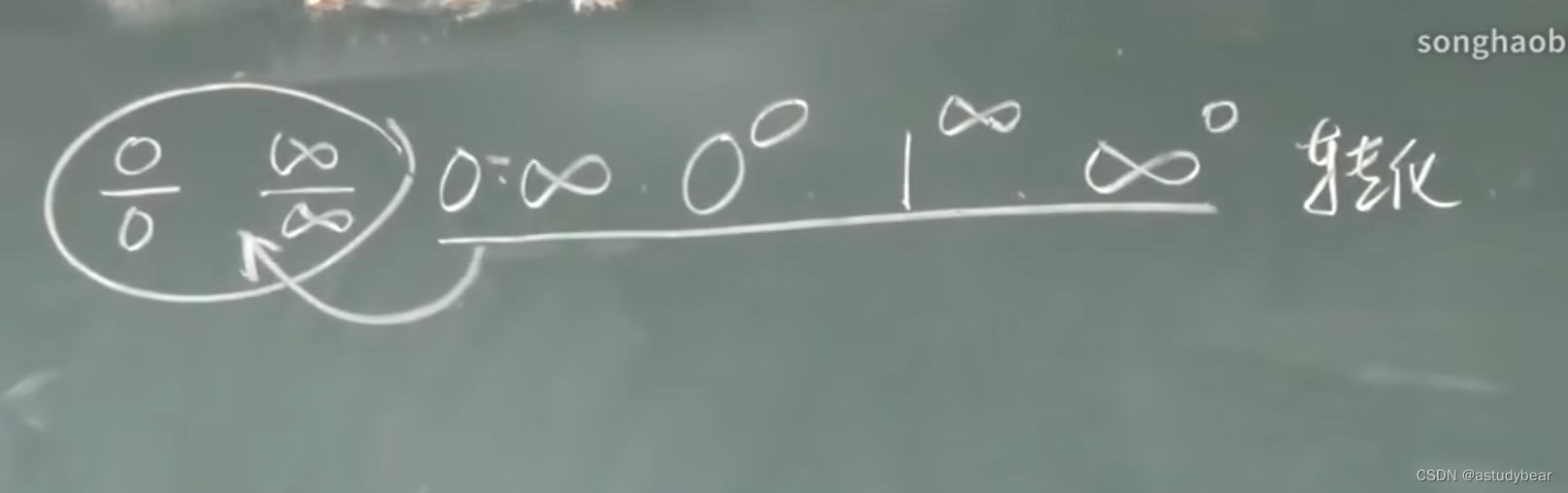
 例题

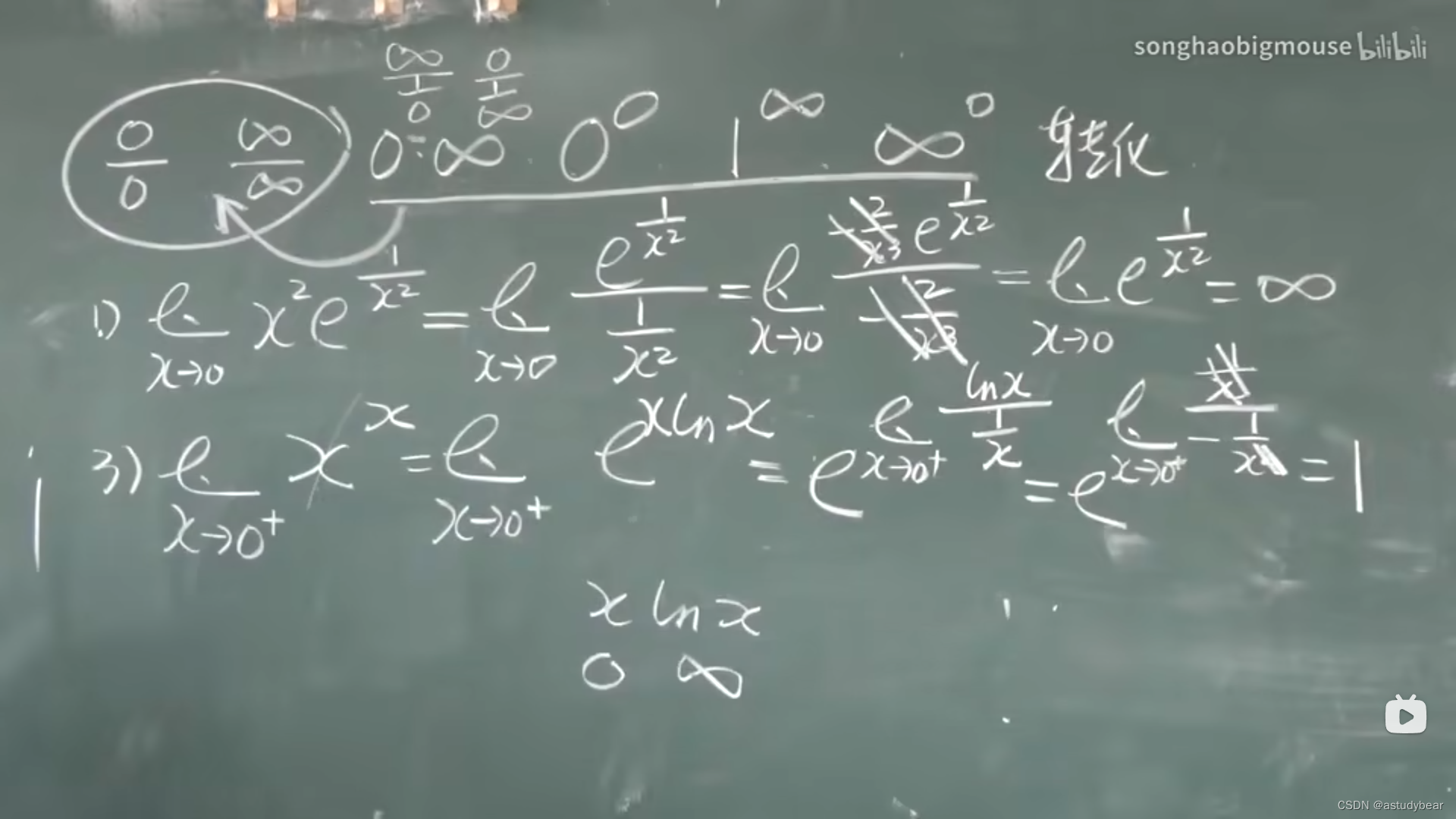
一般像第三题这种上下都有x的，可以先换成e的ln****次方，然后再去“玩”

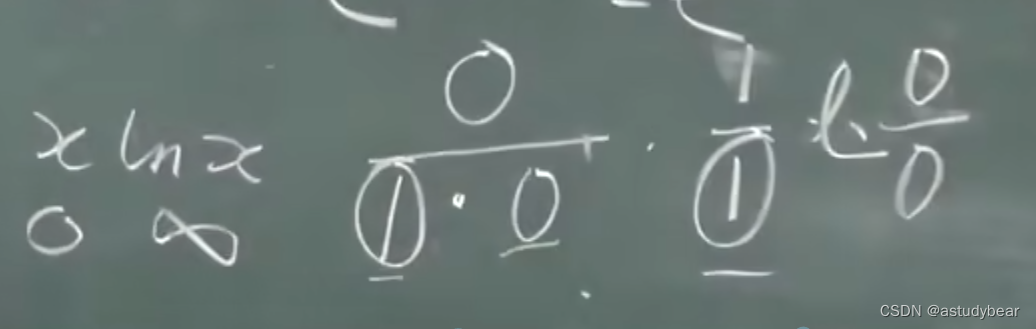
像这种情况直接算结果会有问题，不如将那个“1”拿出去再来玩

3.3单调性 凹凸性

单调性定义

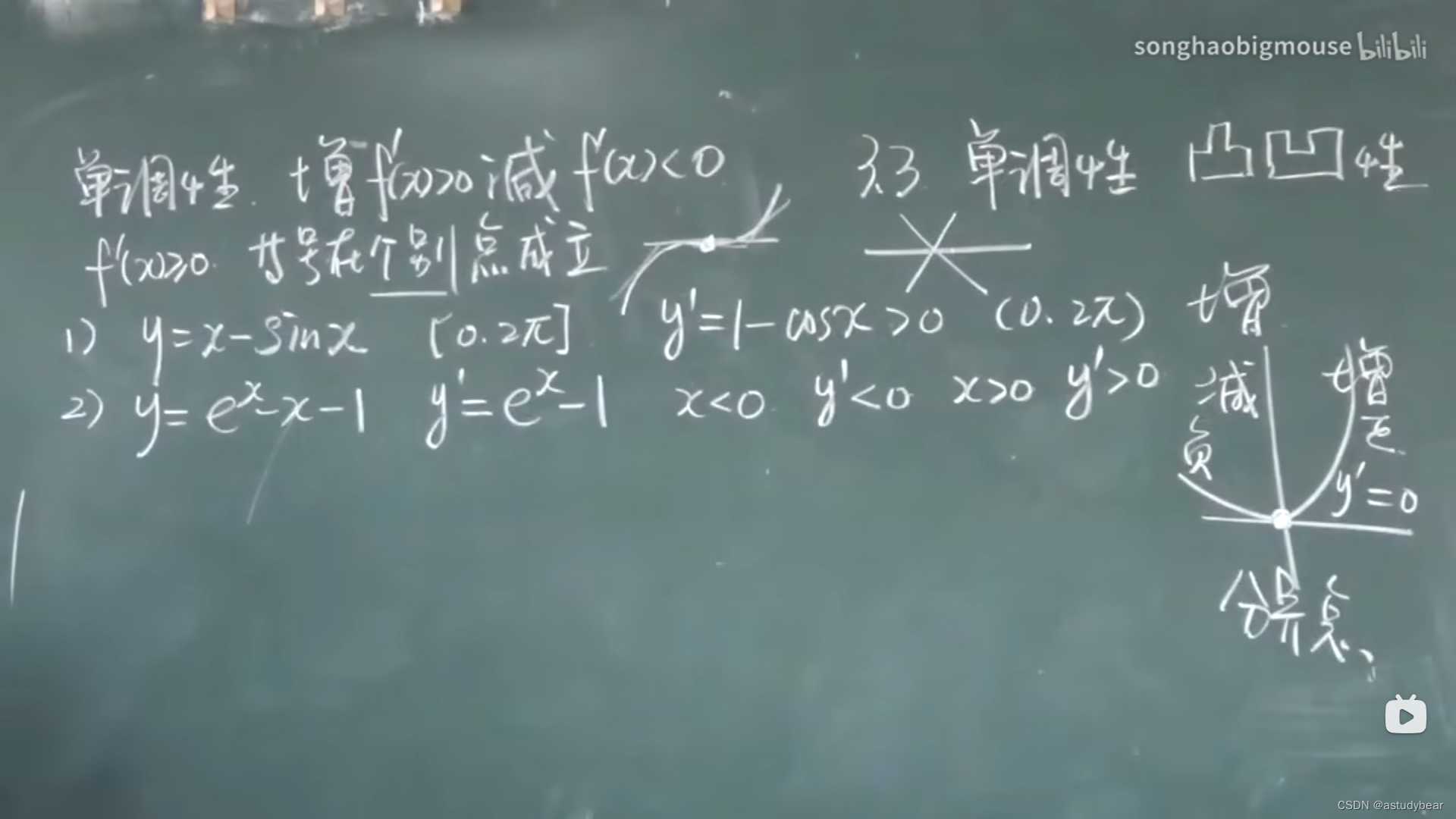
例题

 

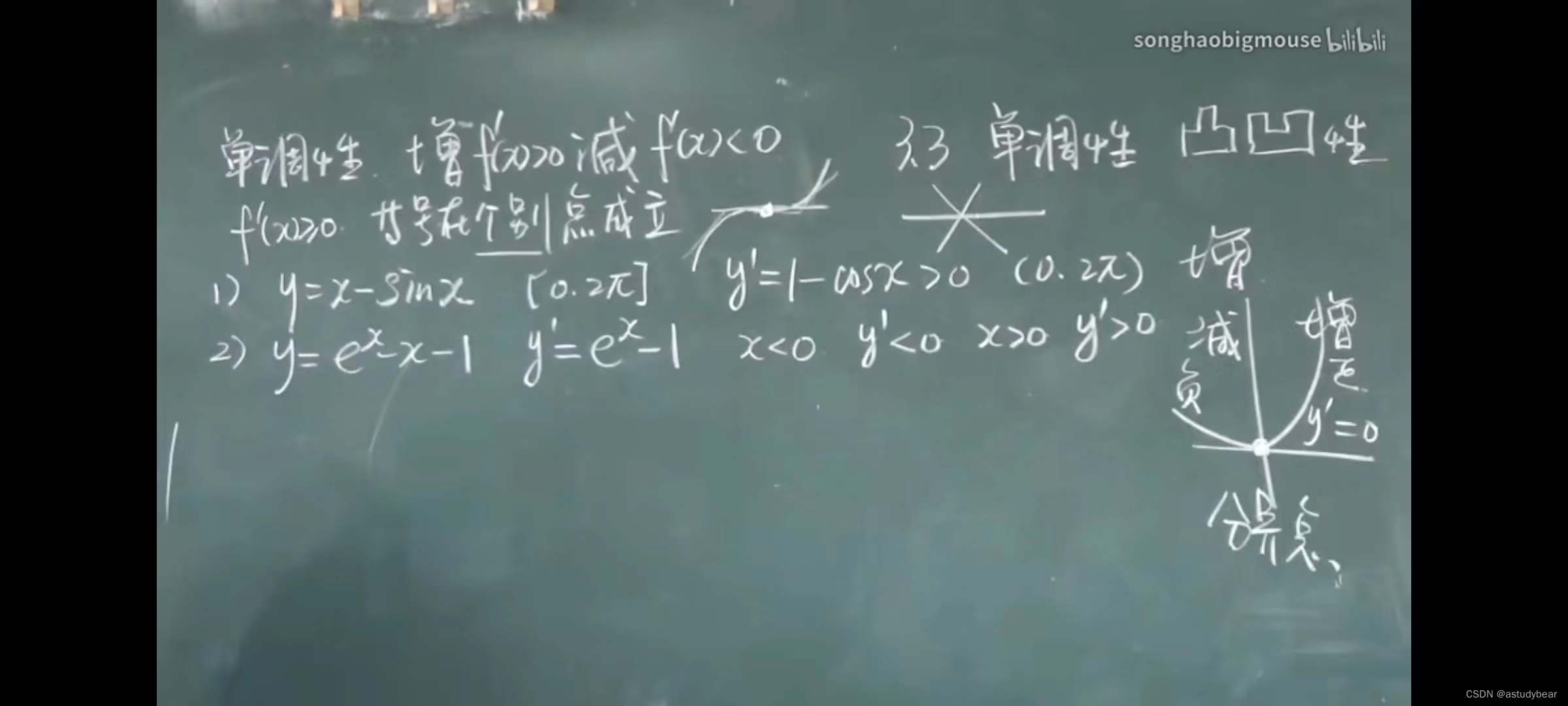
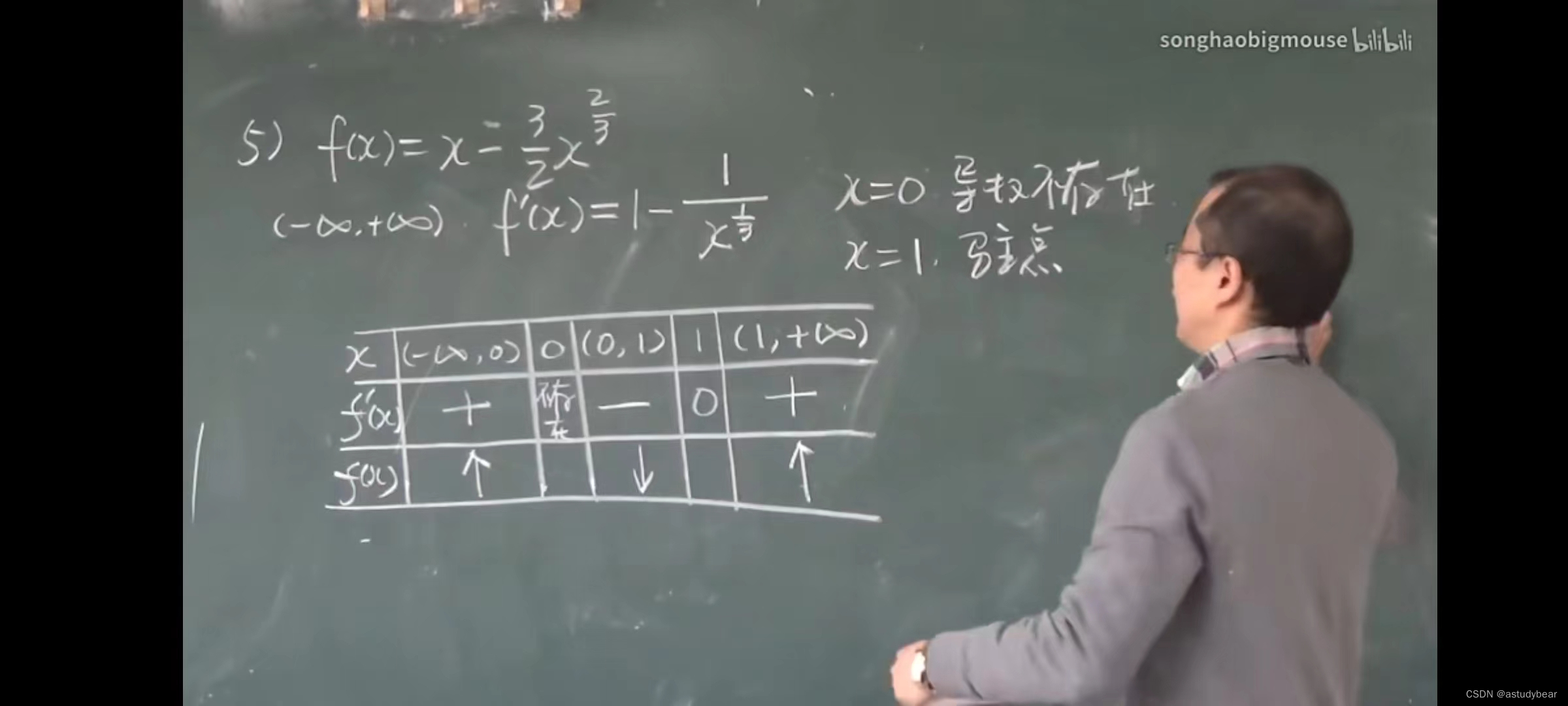
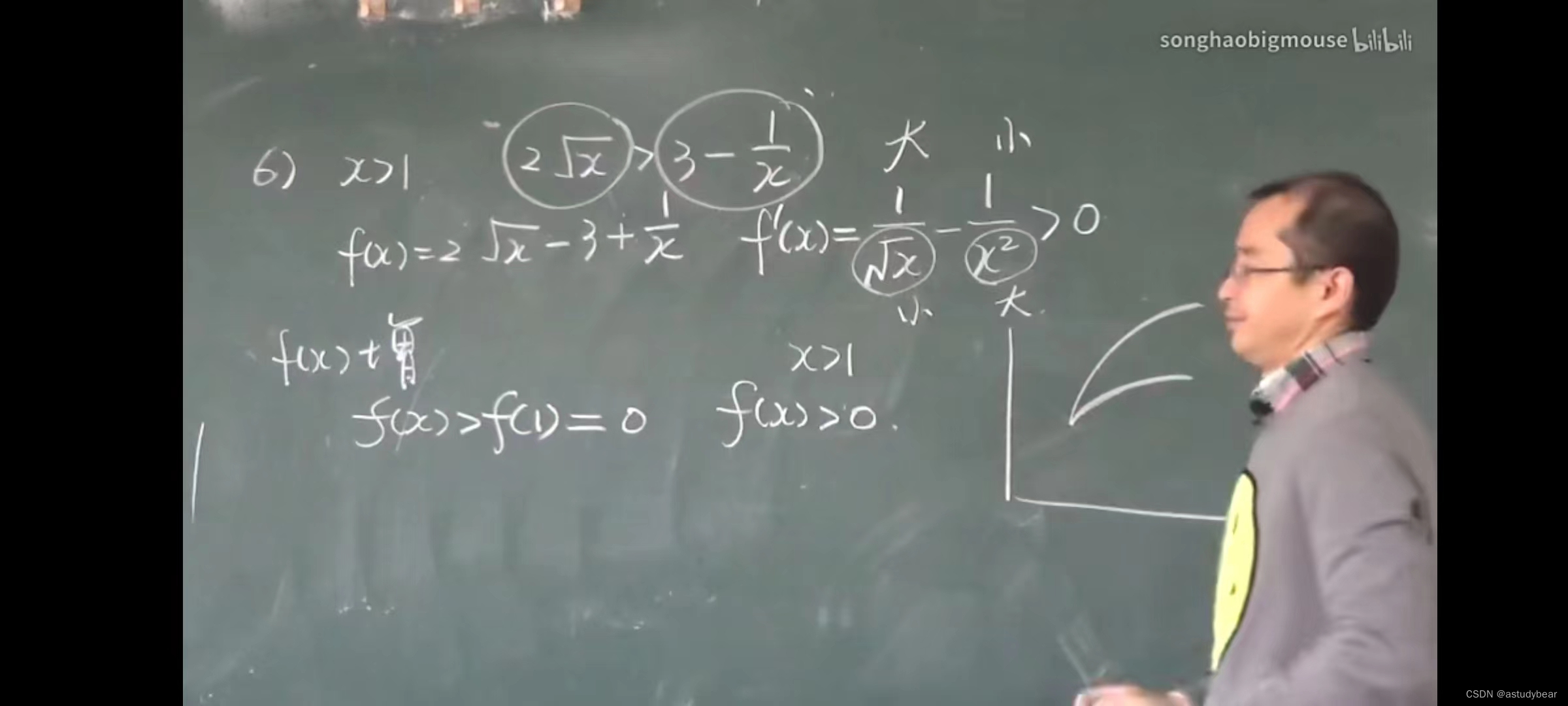
 凹凸性定义

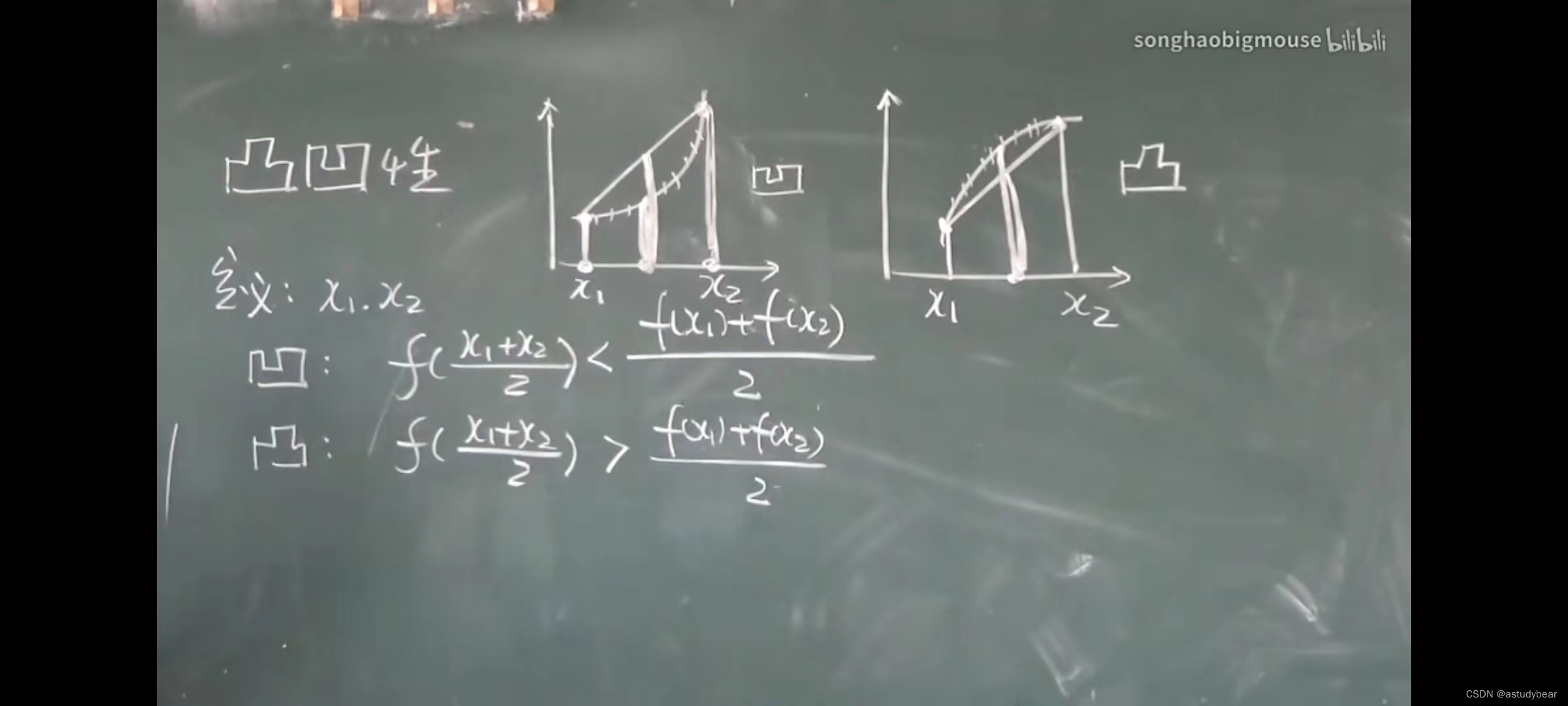
二阶导数大于0是凹，小于0是凸

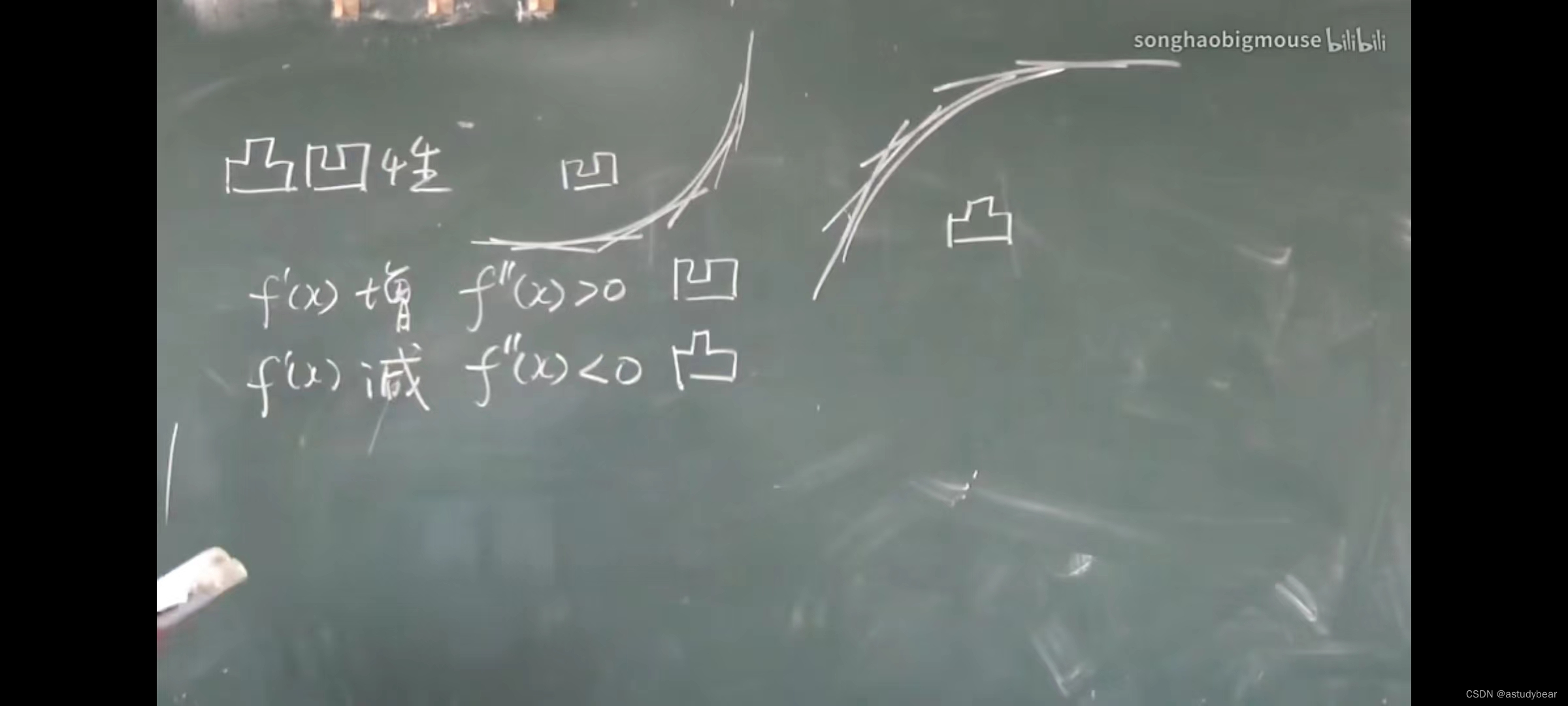
 证明

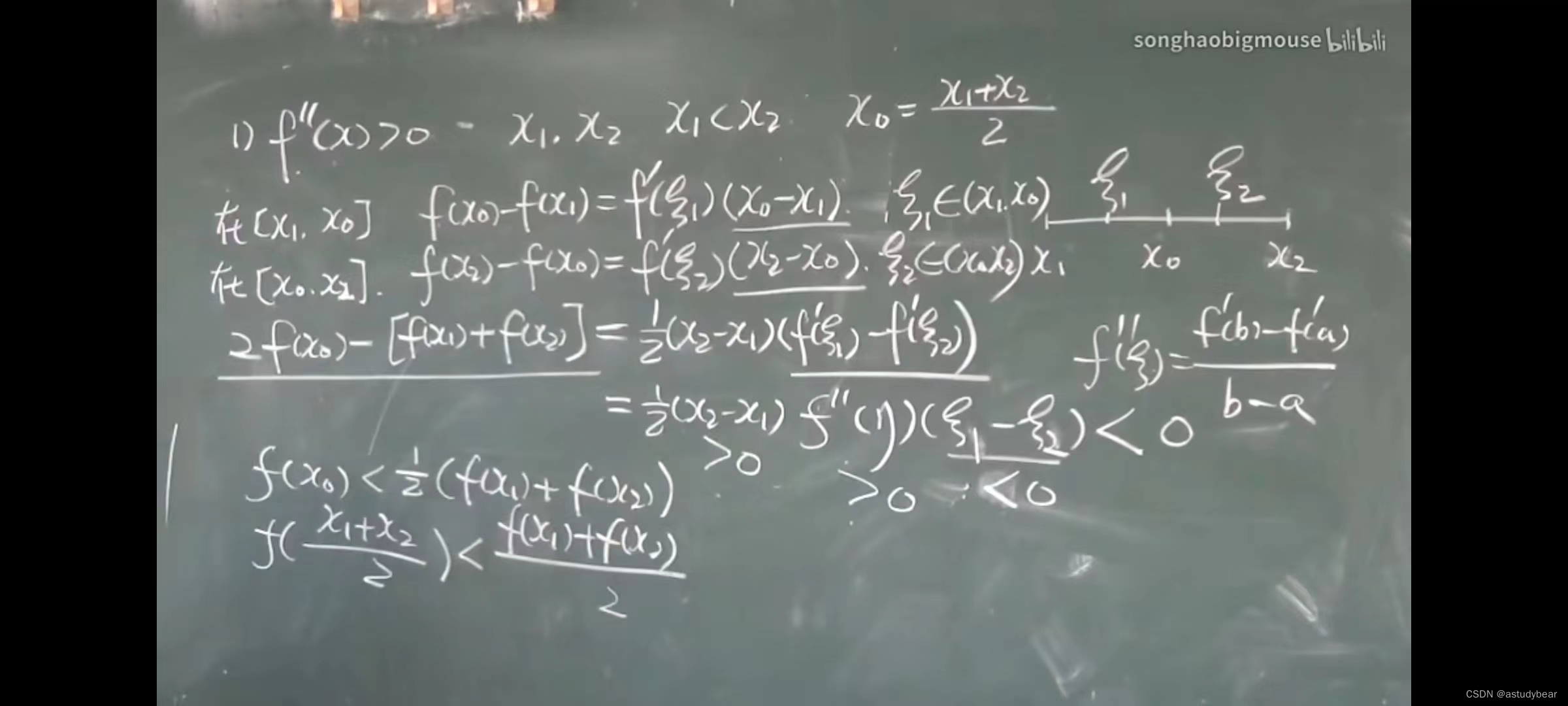
 例题

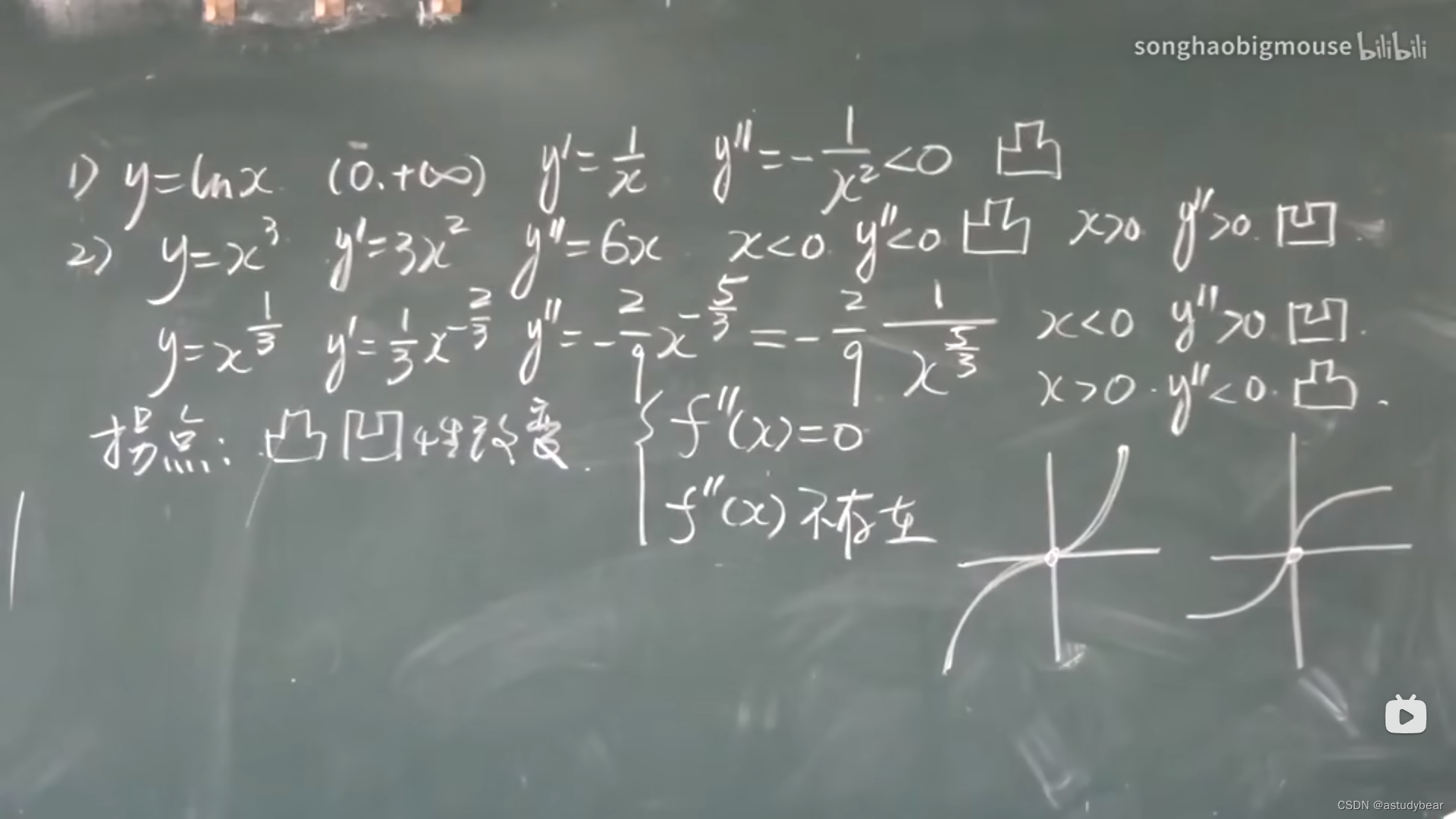
 拐点：①二阶导数=0或不存在可能是拐点。②左右两边凹凸性不同

例题

 

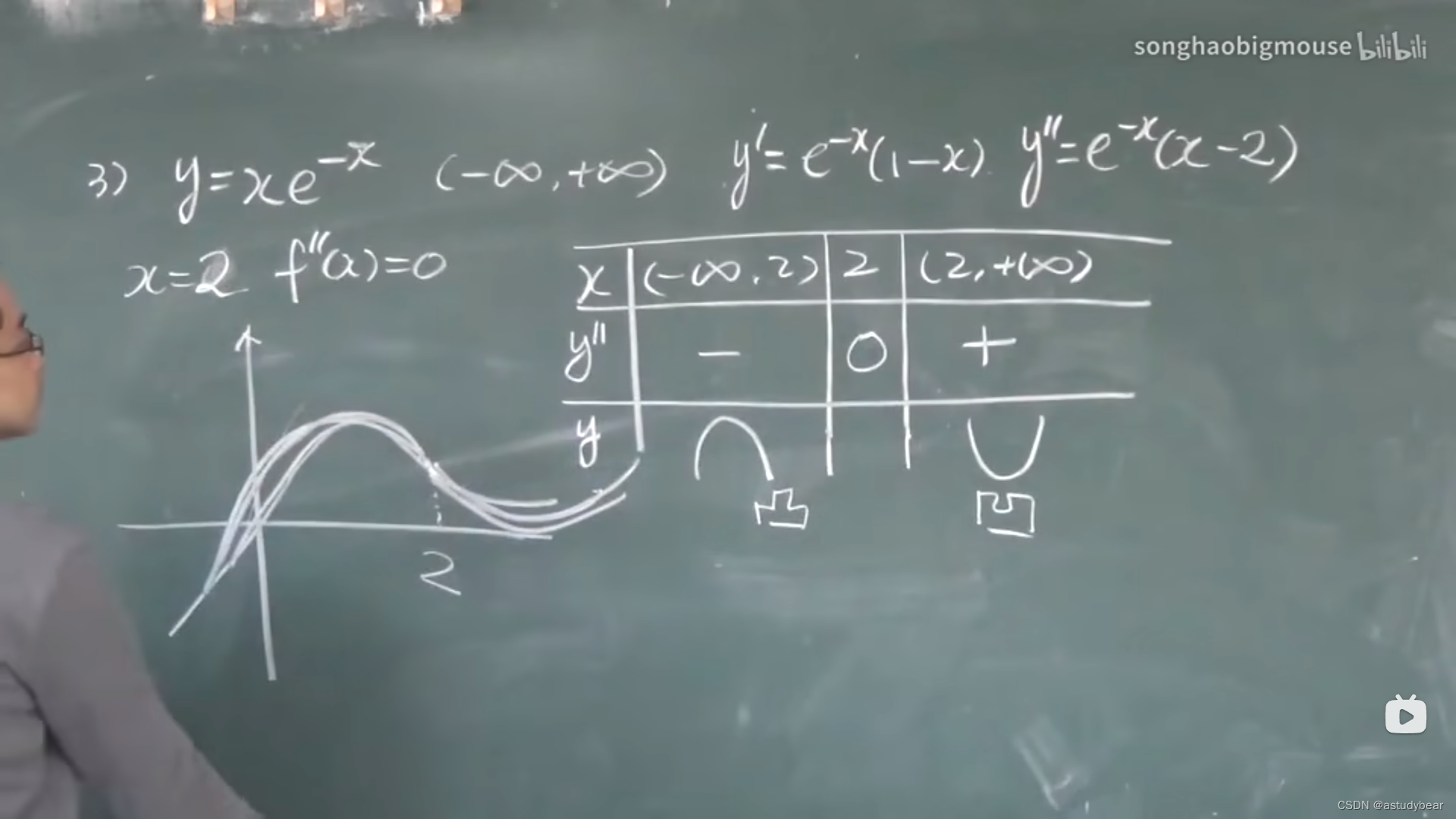
 总结：

单调性，看定义域，然后求导数看大小，大就单调增，小就单调减

 凹凸性，常见的题型解法：先求一阶导数然后二阶，找二阶不存在和等于0的点，然后把定义域分成不同的小区间，然后看区间上的凸凹性，如果过了那个点凸凹性变了就是拐点

3.4极值和最值

极值定义

定理

 

极值的解题步骤

①解定义域，求导数=0和不存在的点

②求导数左右的符号，然后看是极大还是极小

③求函数值

例题：

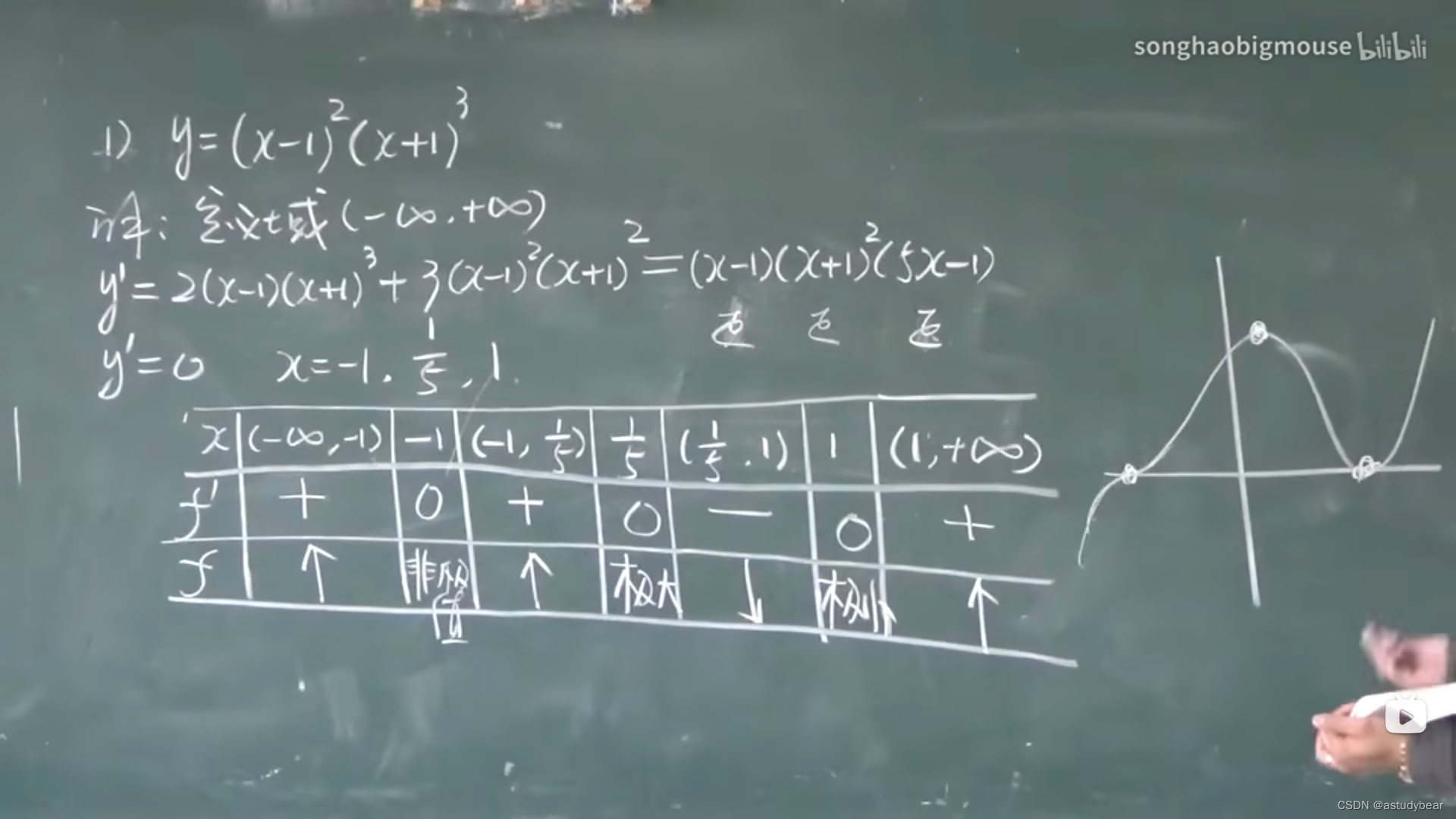
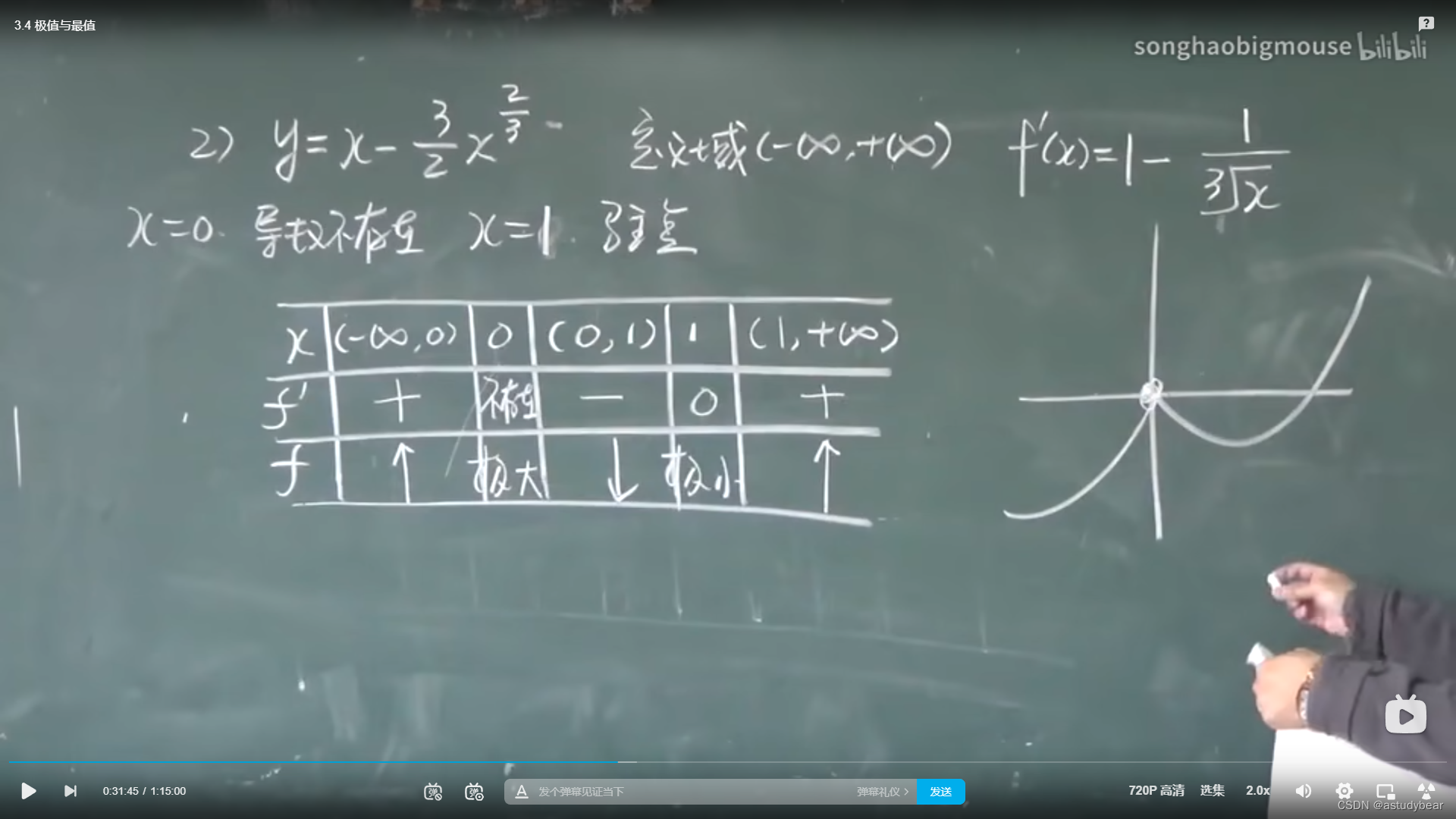
 定理

 例题

4.1不定积分

 简单讲就是找f(x)的原函数然后再加上c

例题以及几何含义

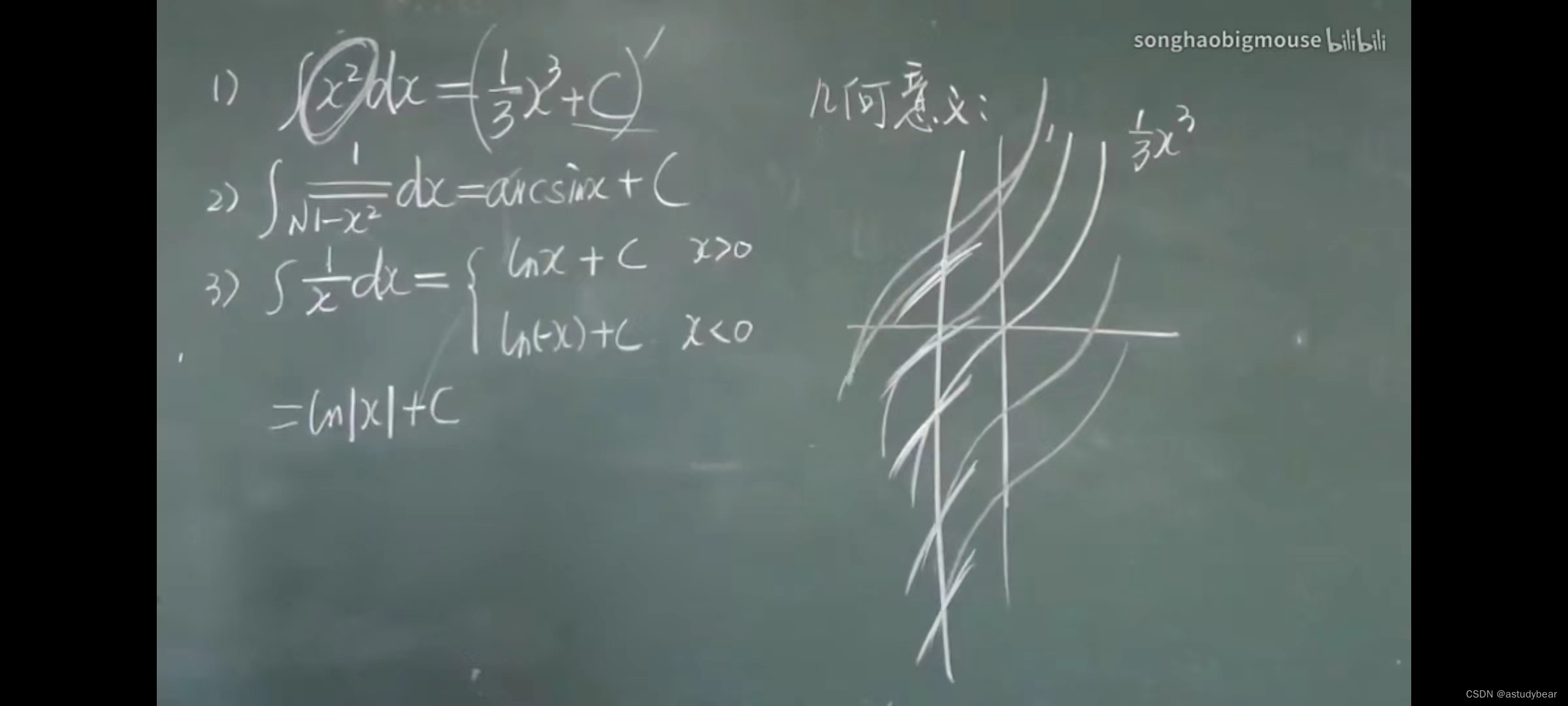
 几何含义:上下平行移动

 

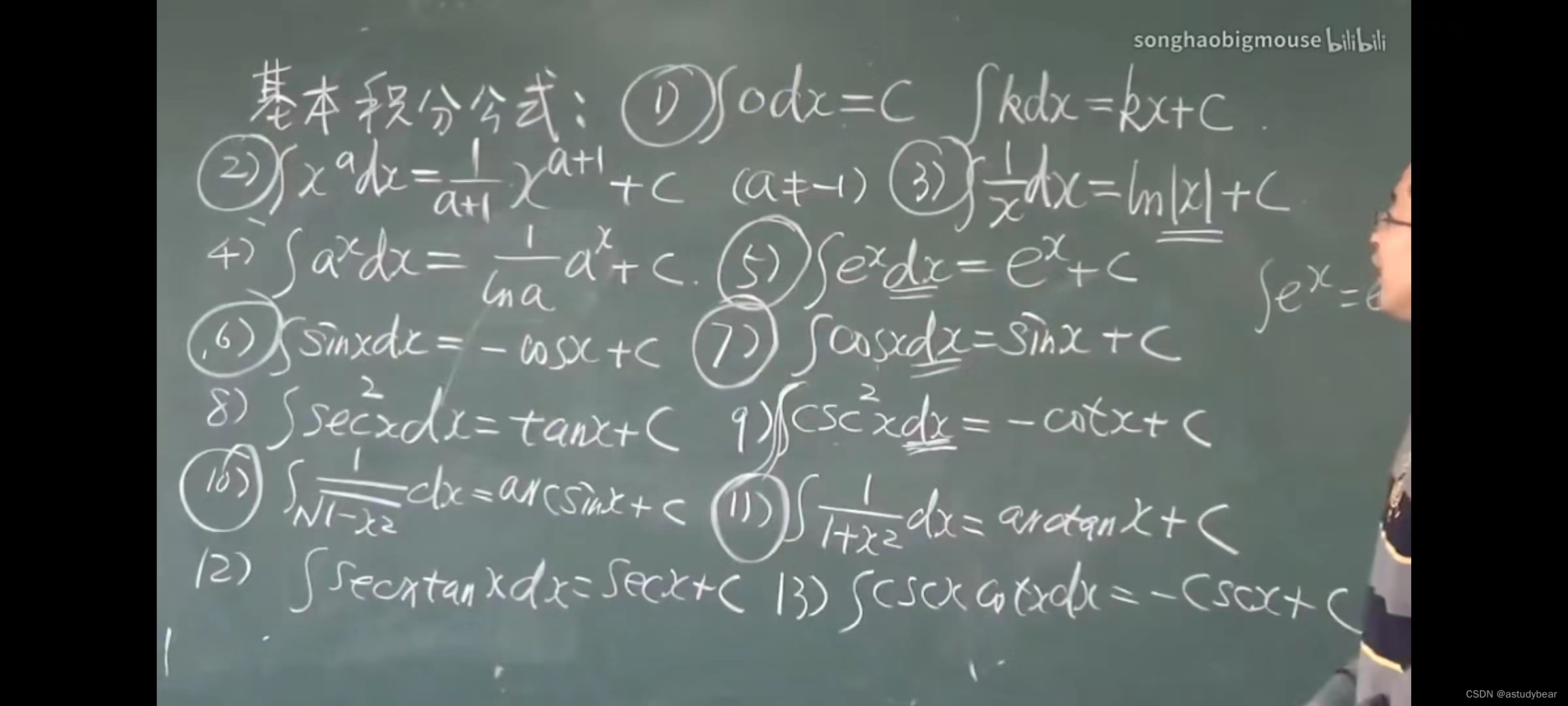
 例题

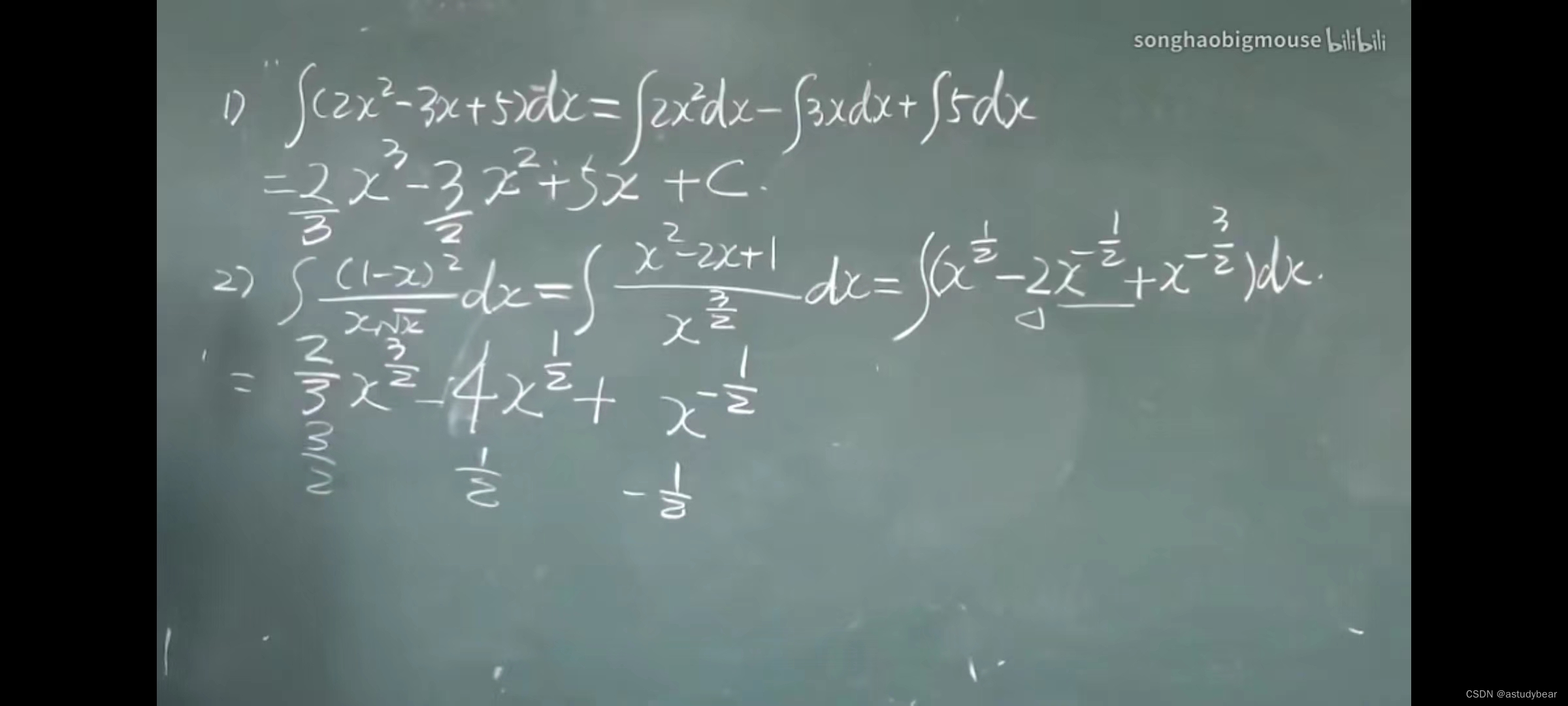
4.2积分法（第一换元积分法）

 例题

 

 

 

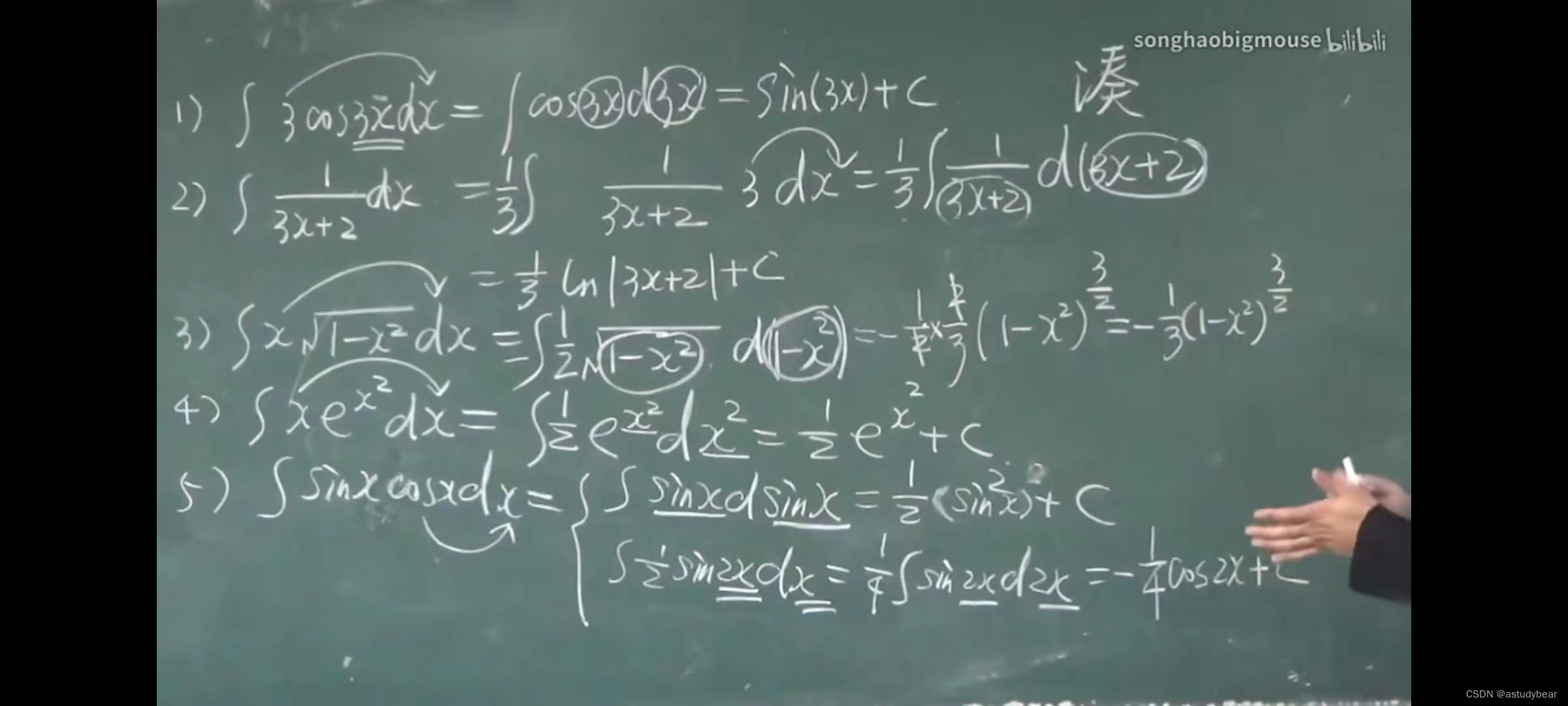
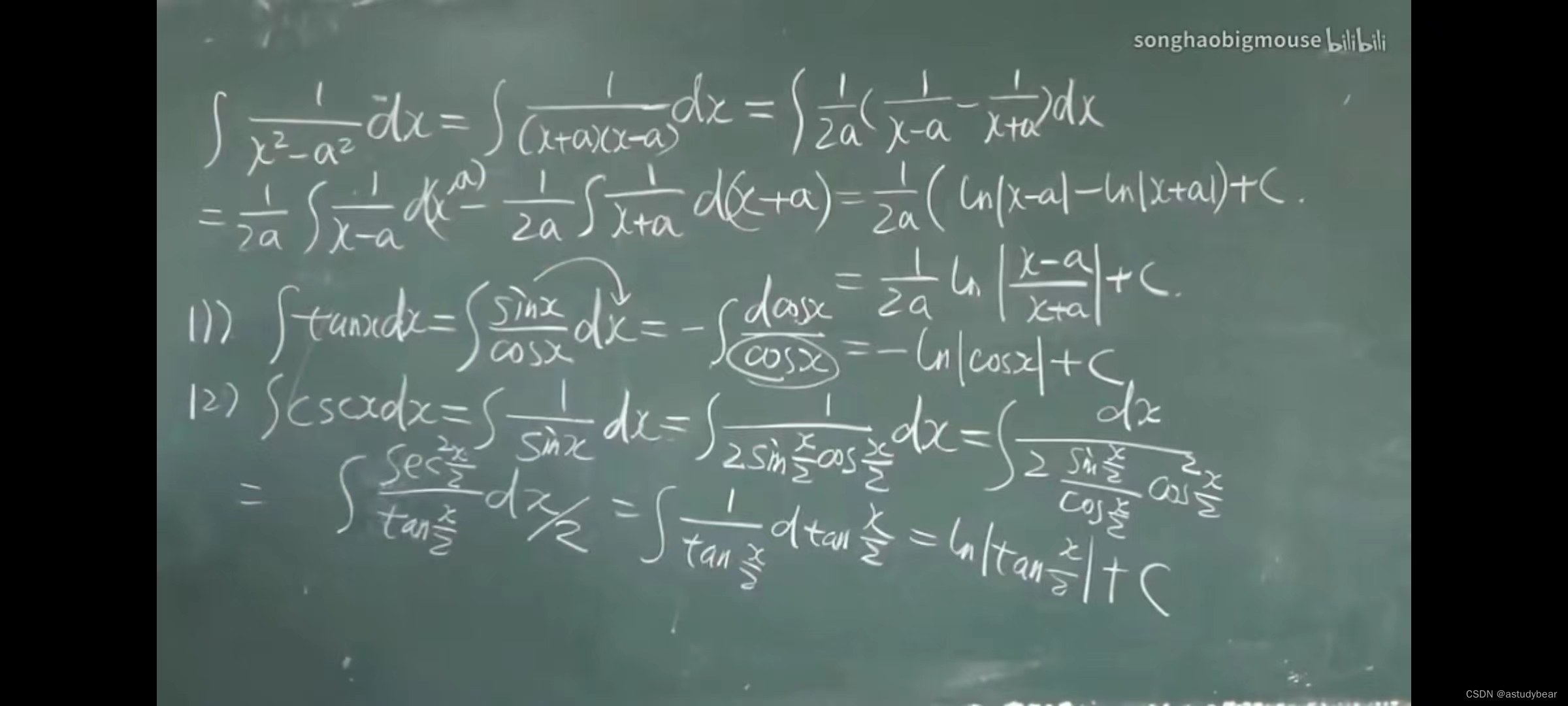
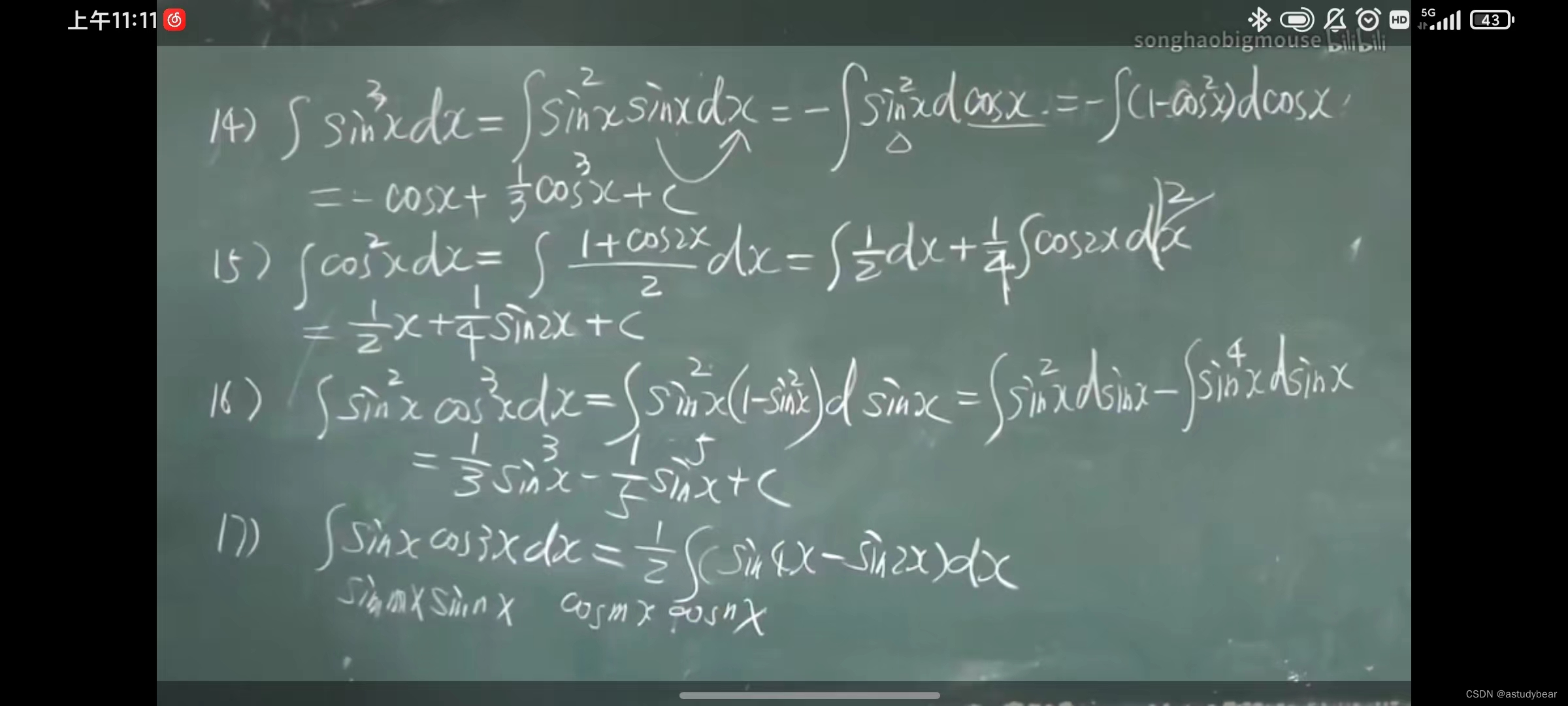
 总结

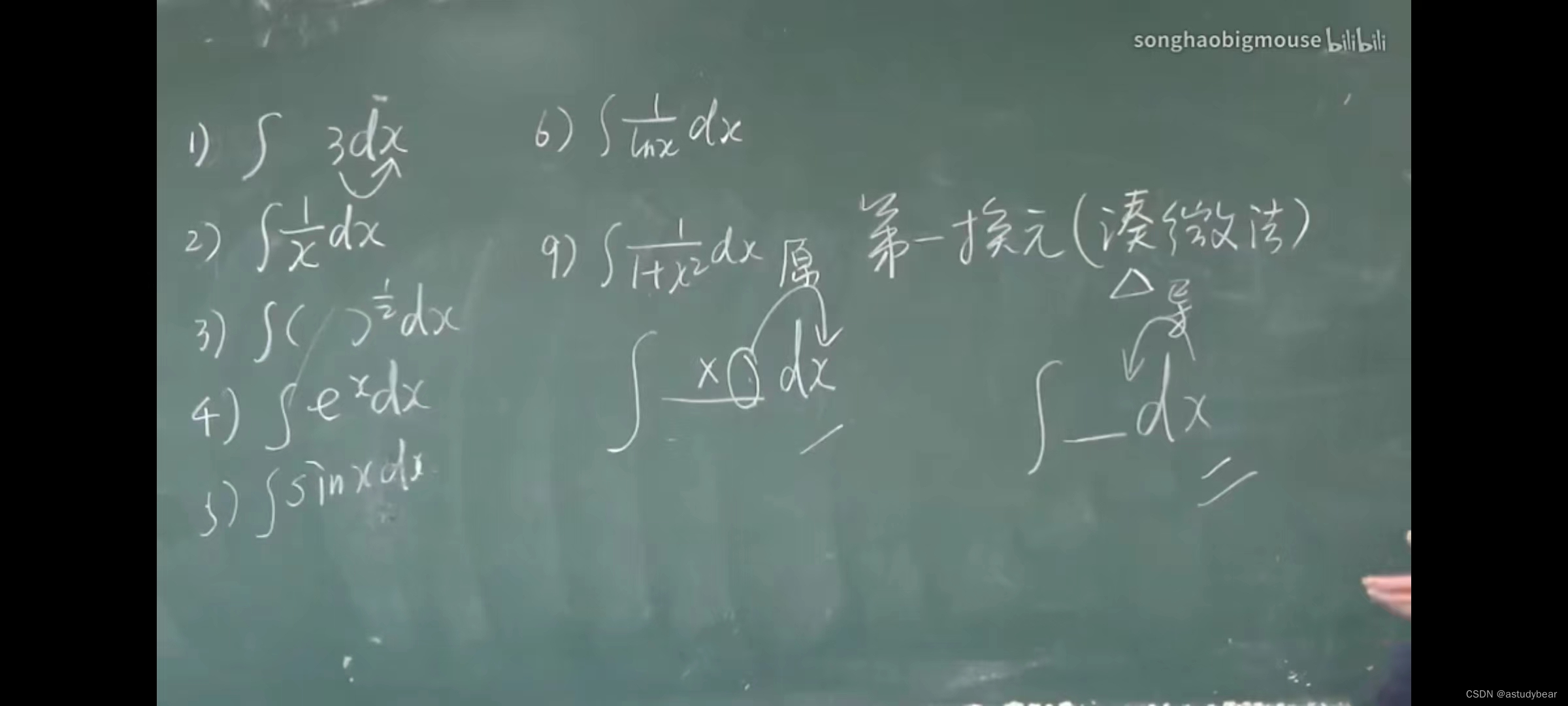
 4.2积分法（第二换元积分法）

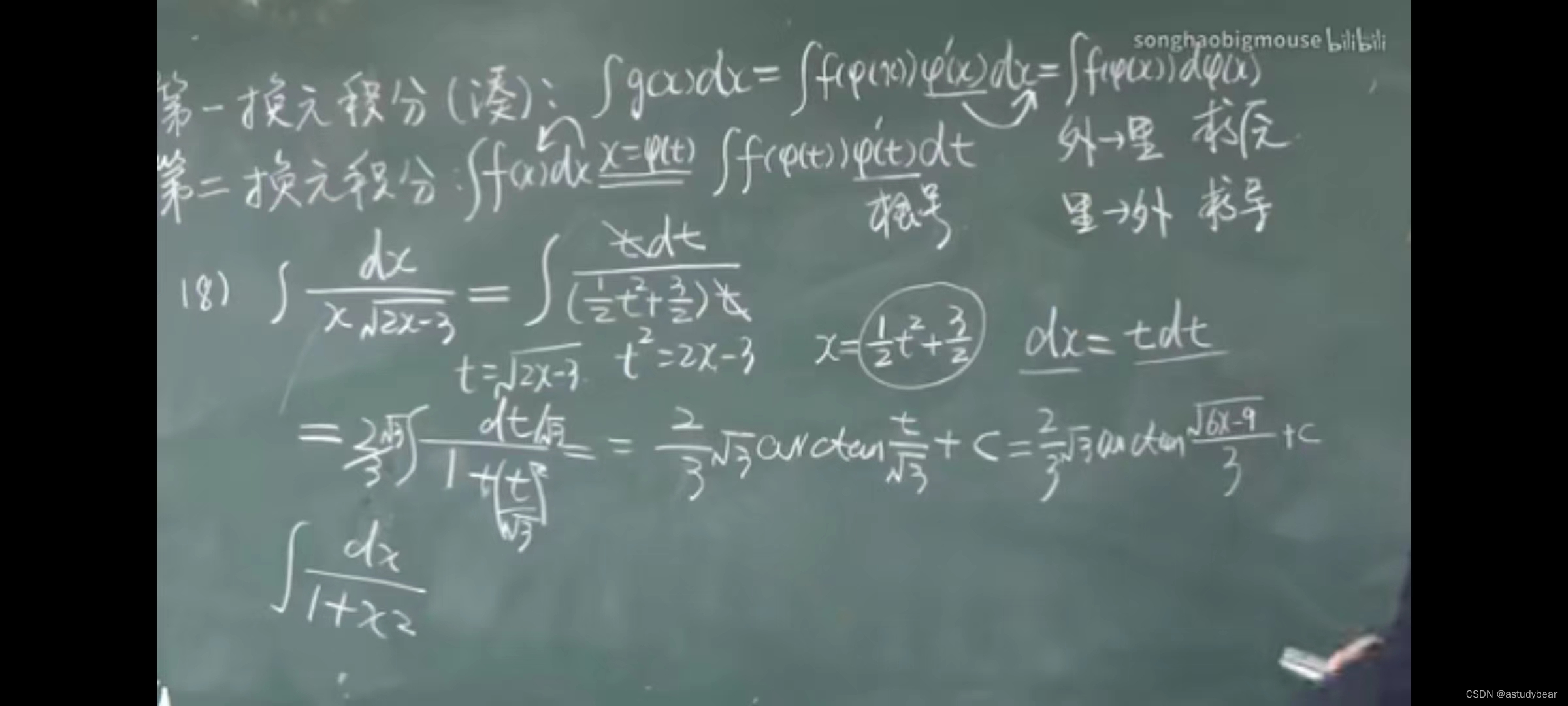
 例题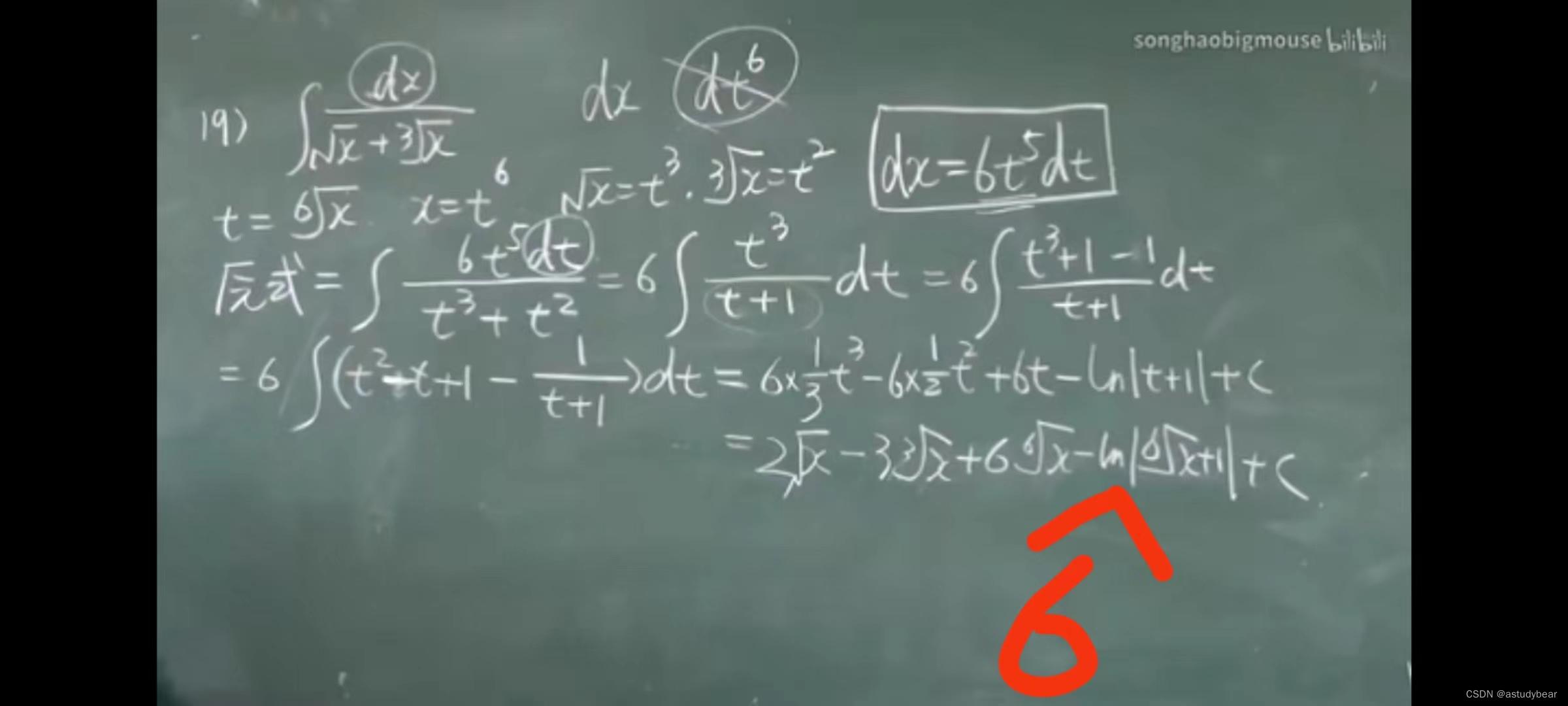

 这题很重要（也挺难）

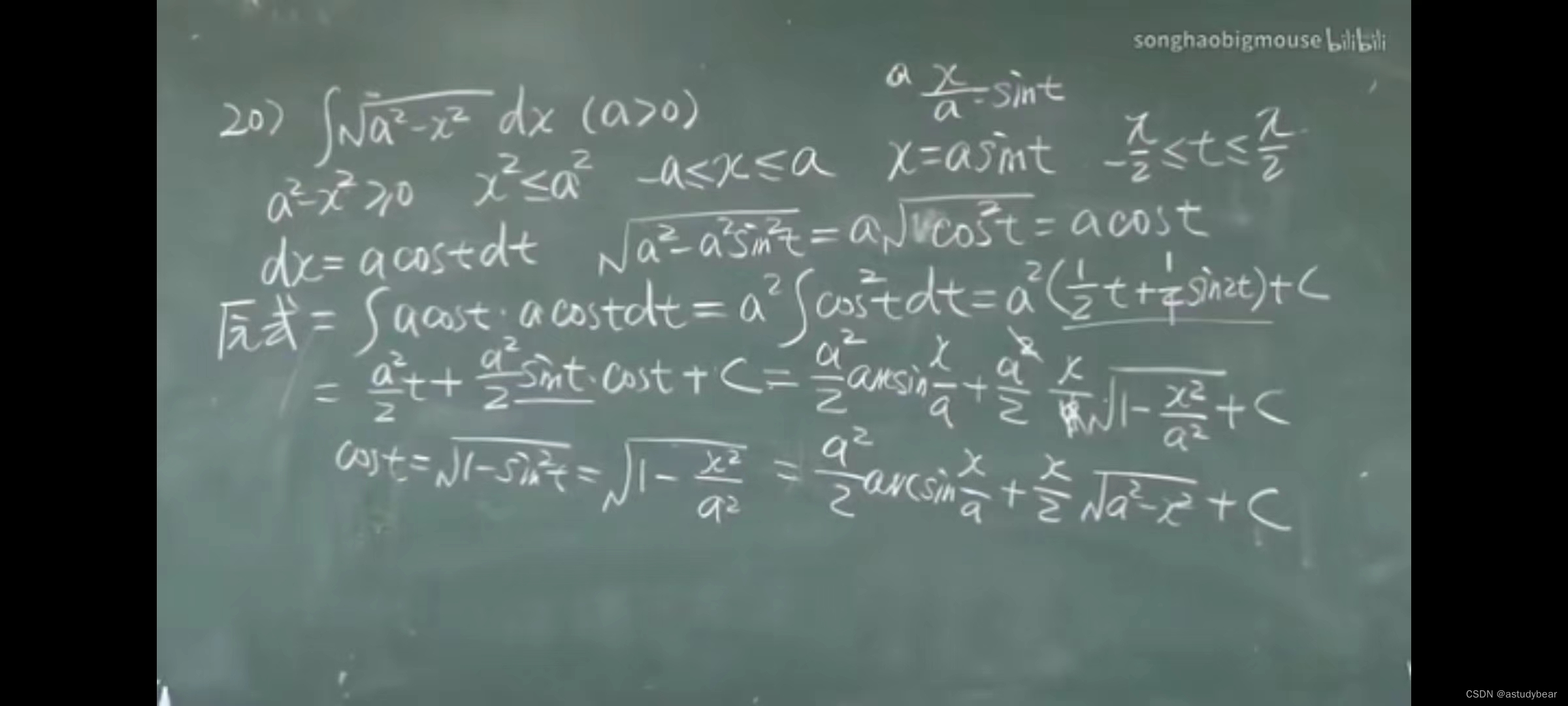
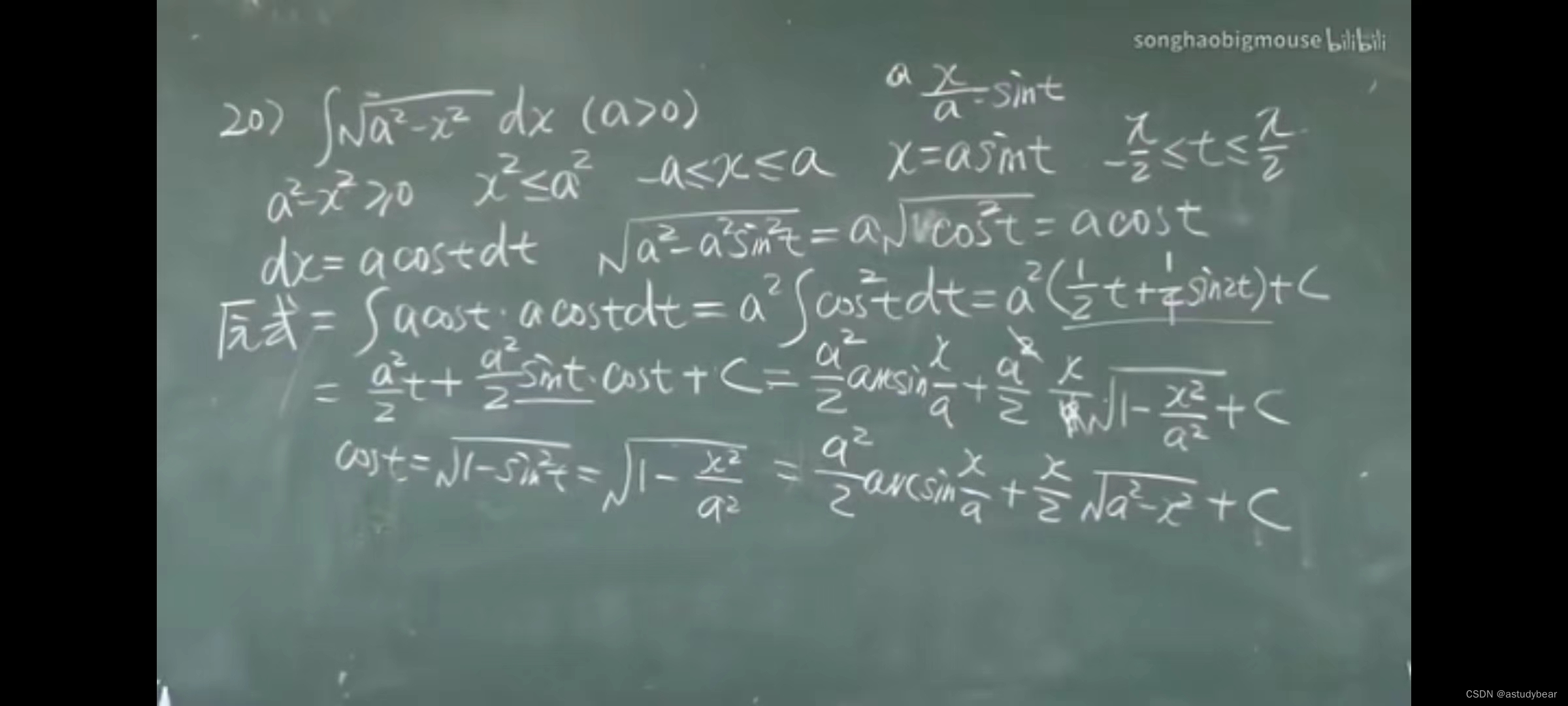
4.2积分法（分部积分法）

 

 

 

 

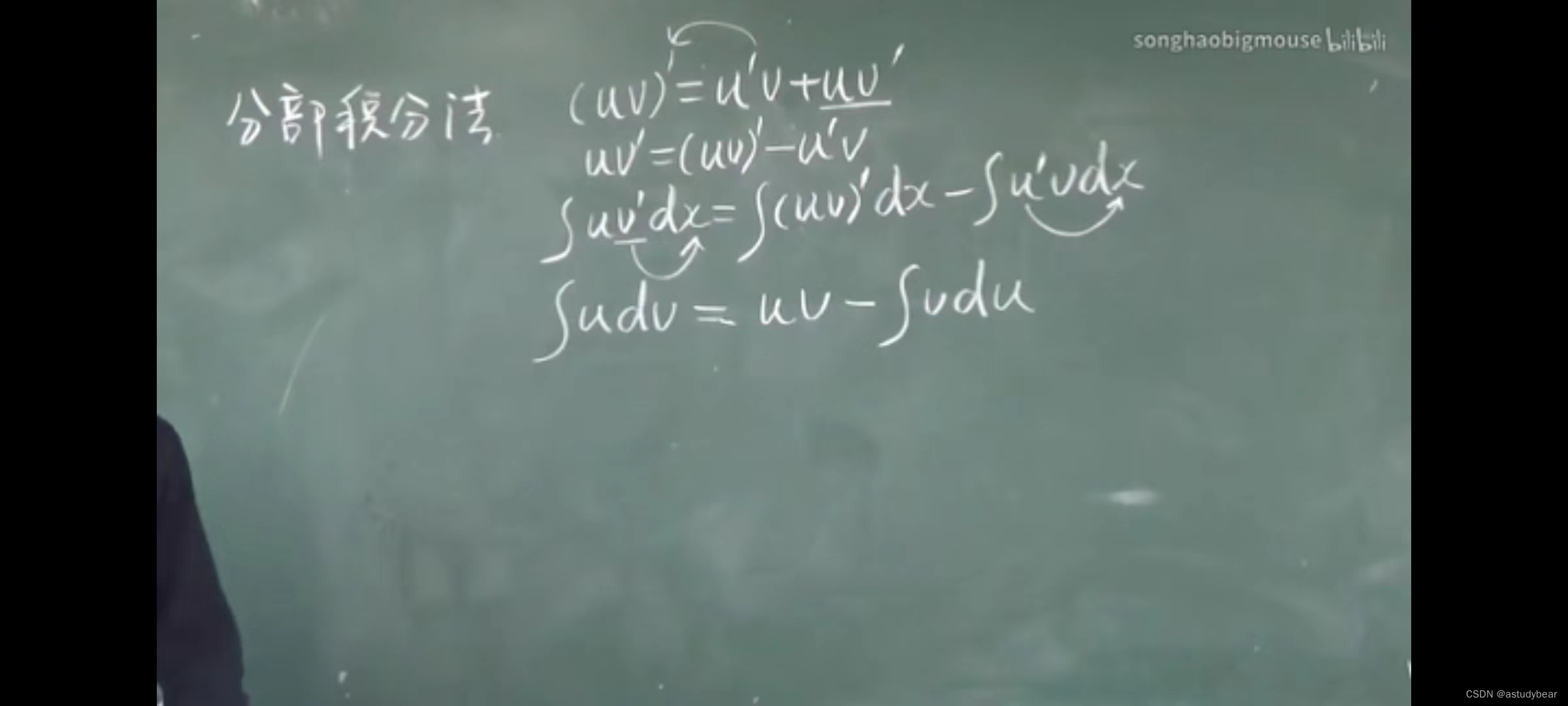
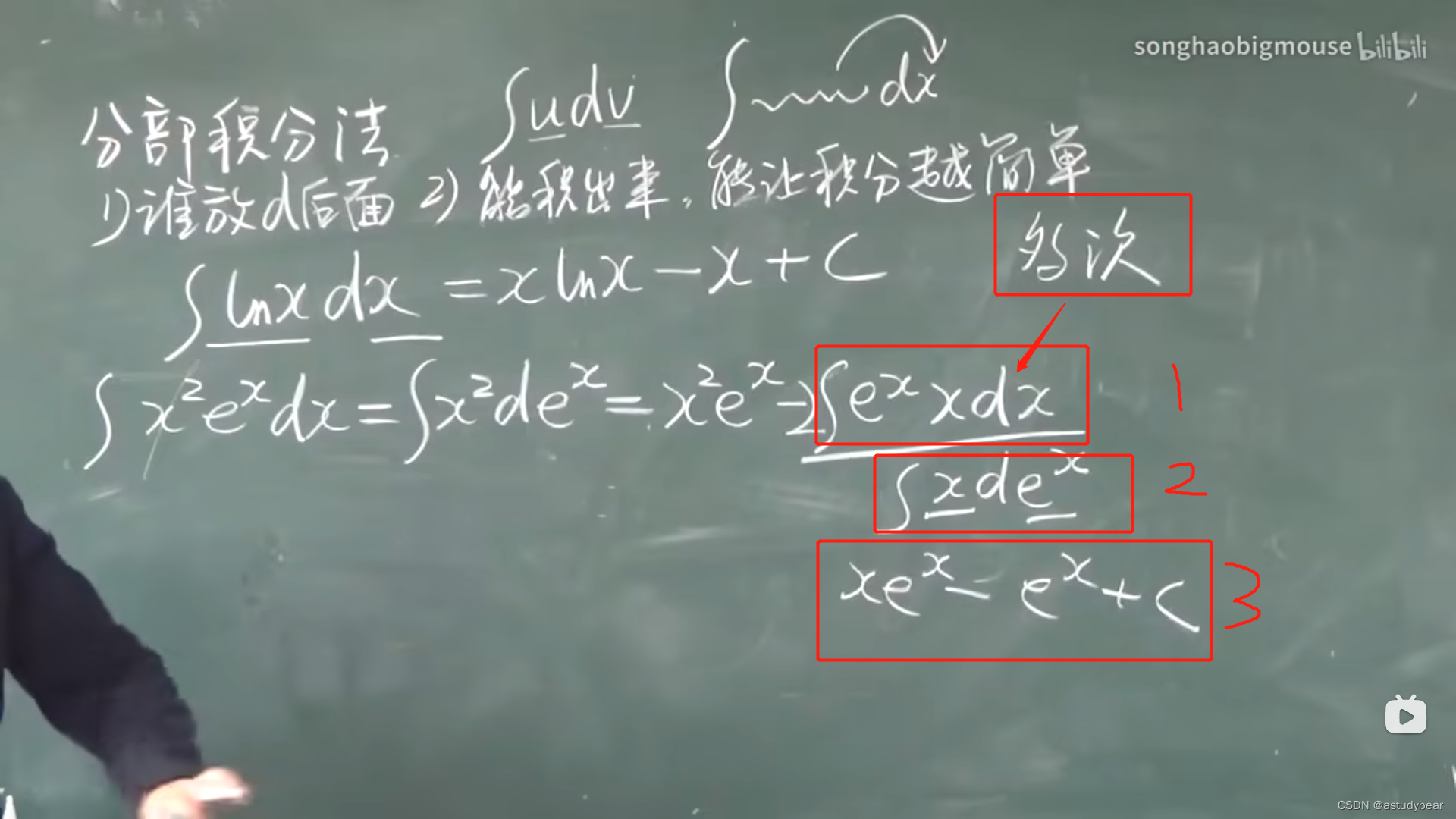
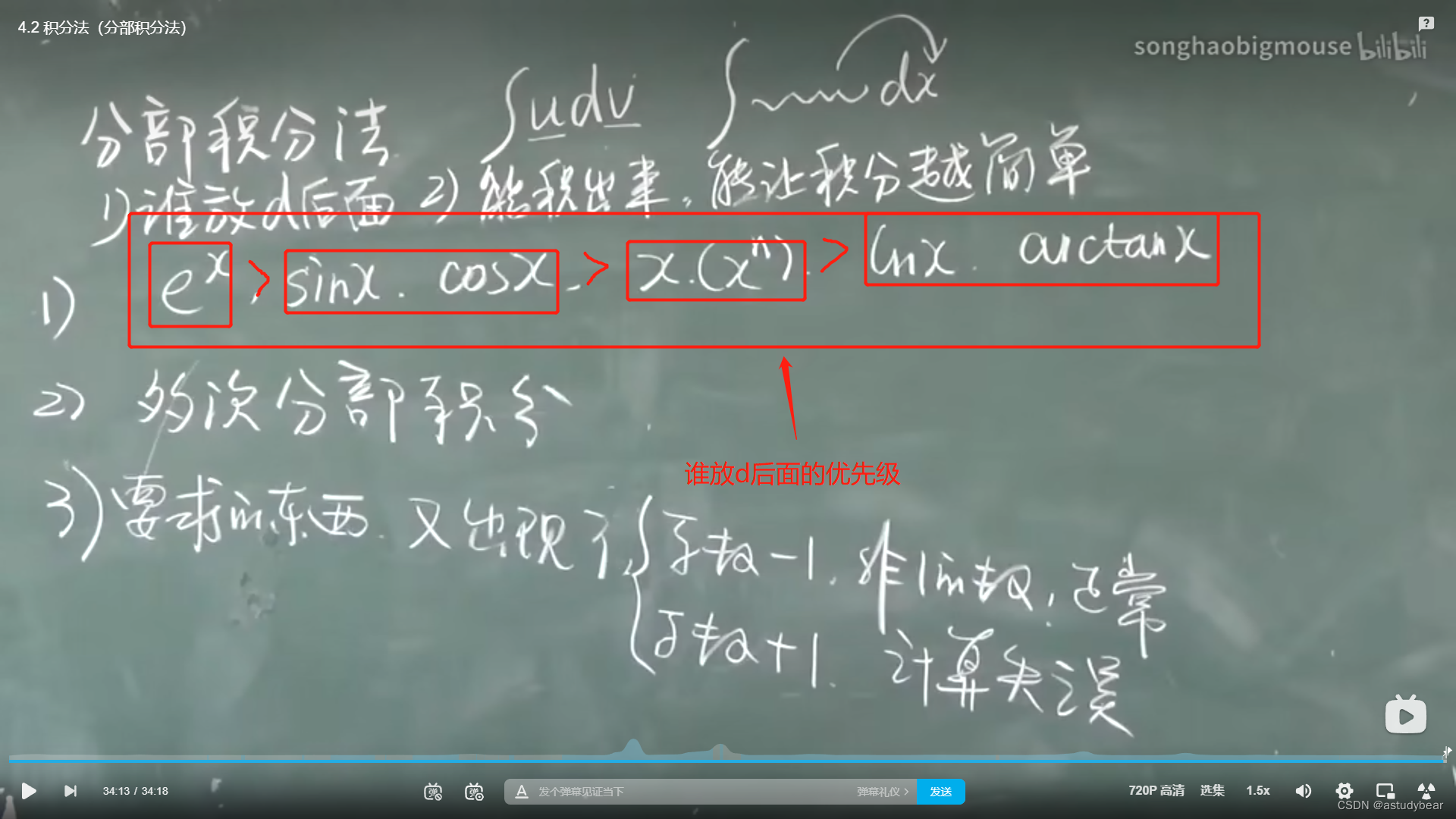
 分部积分法有一个现象，如果你要求的东西，它又出现了，那么分情况

如果系数是-1或者非1，不用担心，把它挪过去

如果系数是+1，那么一定是你的计算出错了，回头检查

4.3有理函数的积分

多项式除法

 分子低分母高

分母二次的

第一类题目：

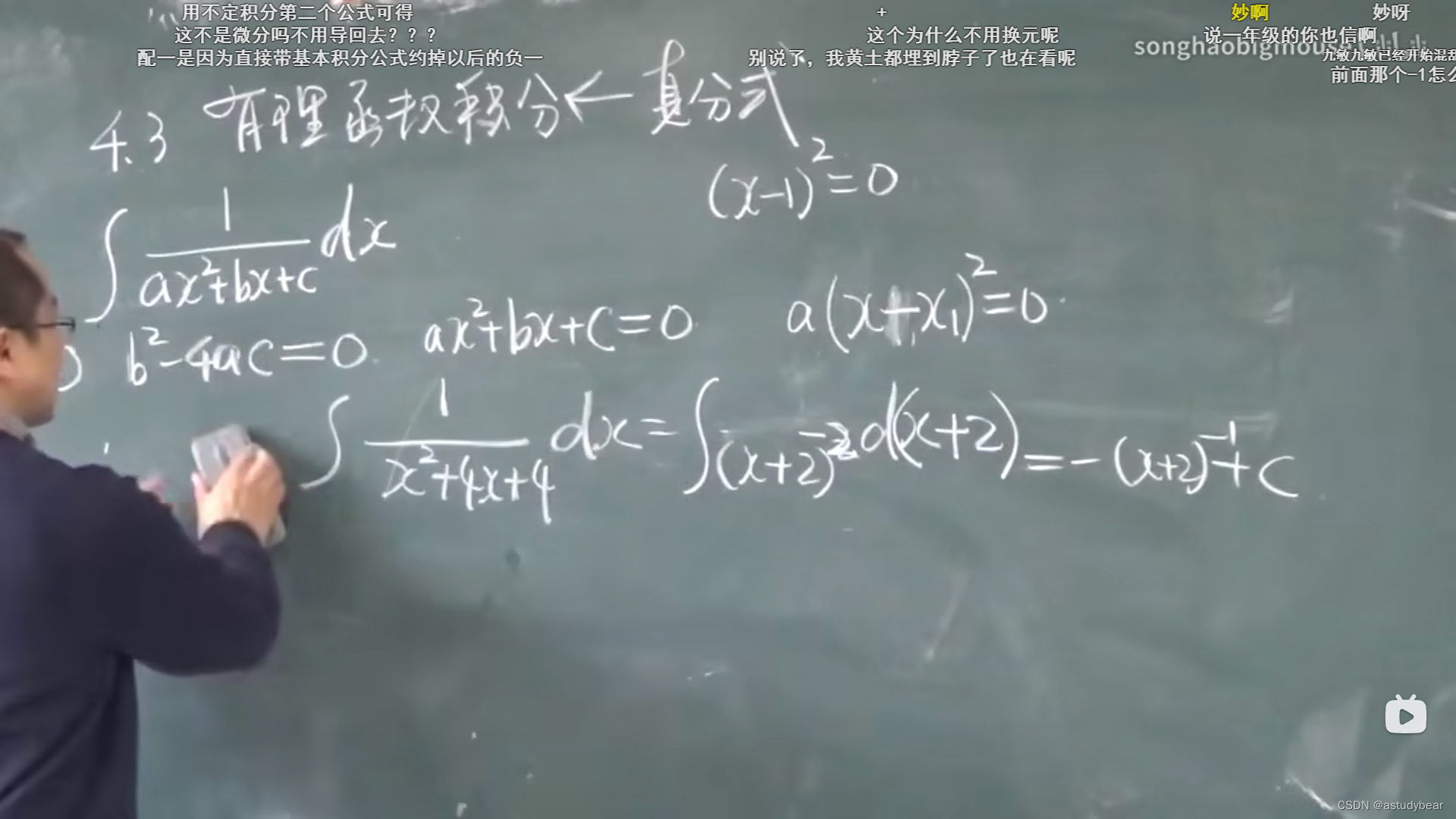
 第三种情况，无实根，分配方然后换元积分，最后用arctan

 第二类题目

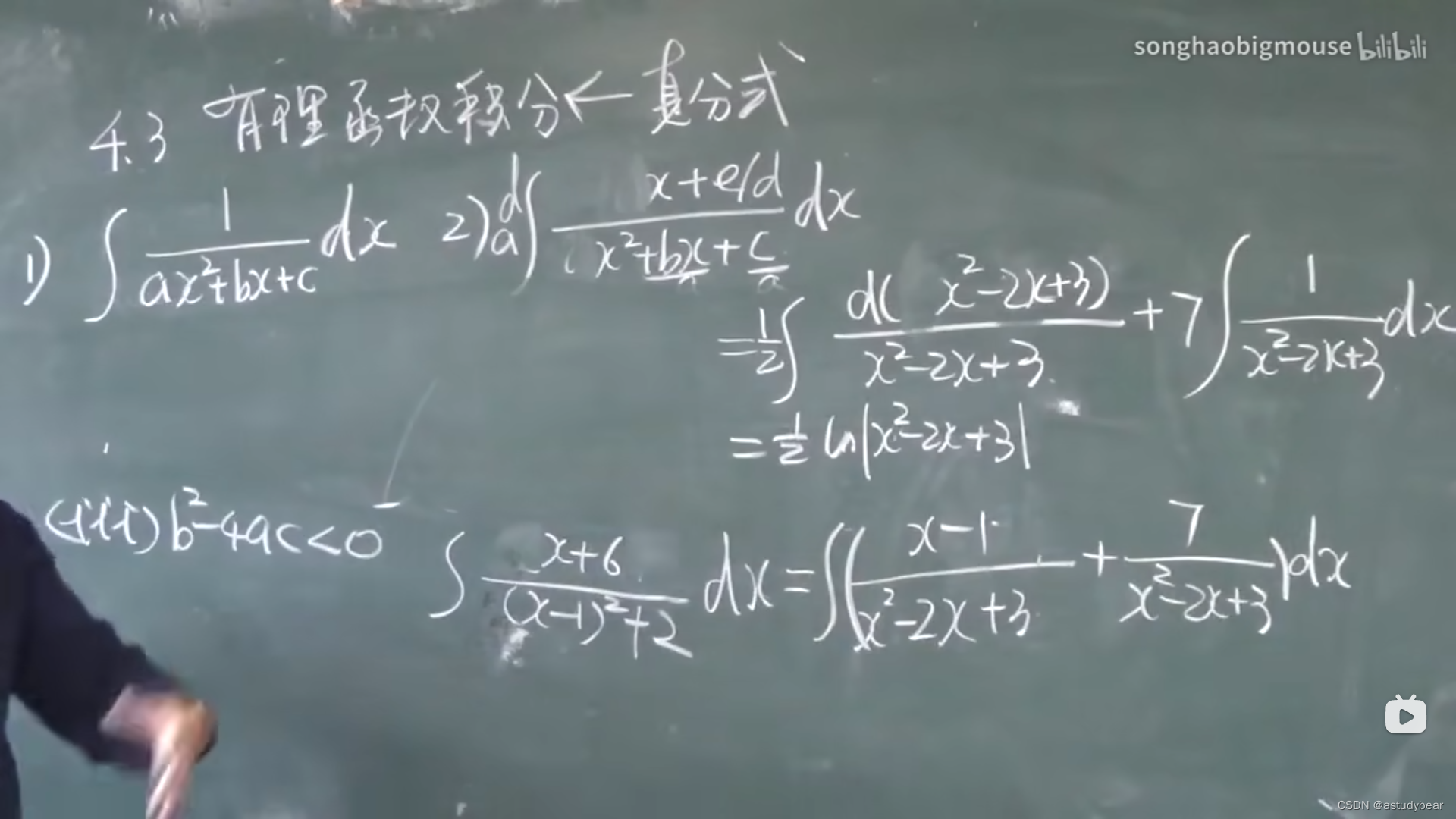
5.1定积分的概念

 定积分的定义

定积分的几何意义（正的是正的，负的是负的，正负都有就相减） 

 例题：（利用定积分的定义来求，这个基本不考，只是了解）

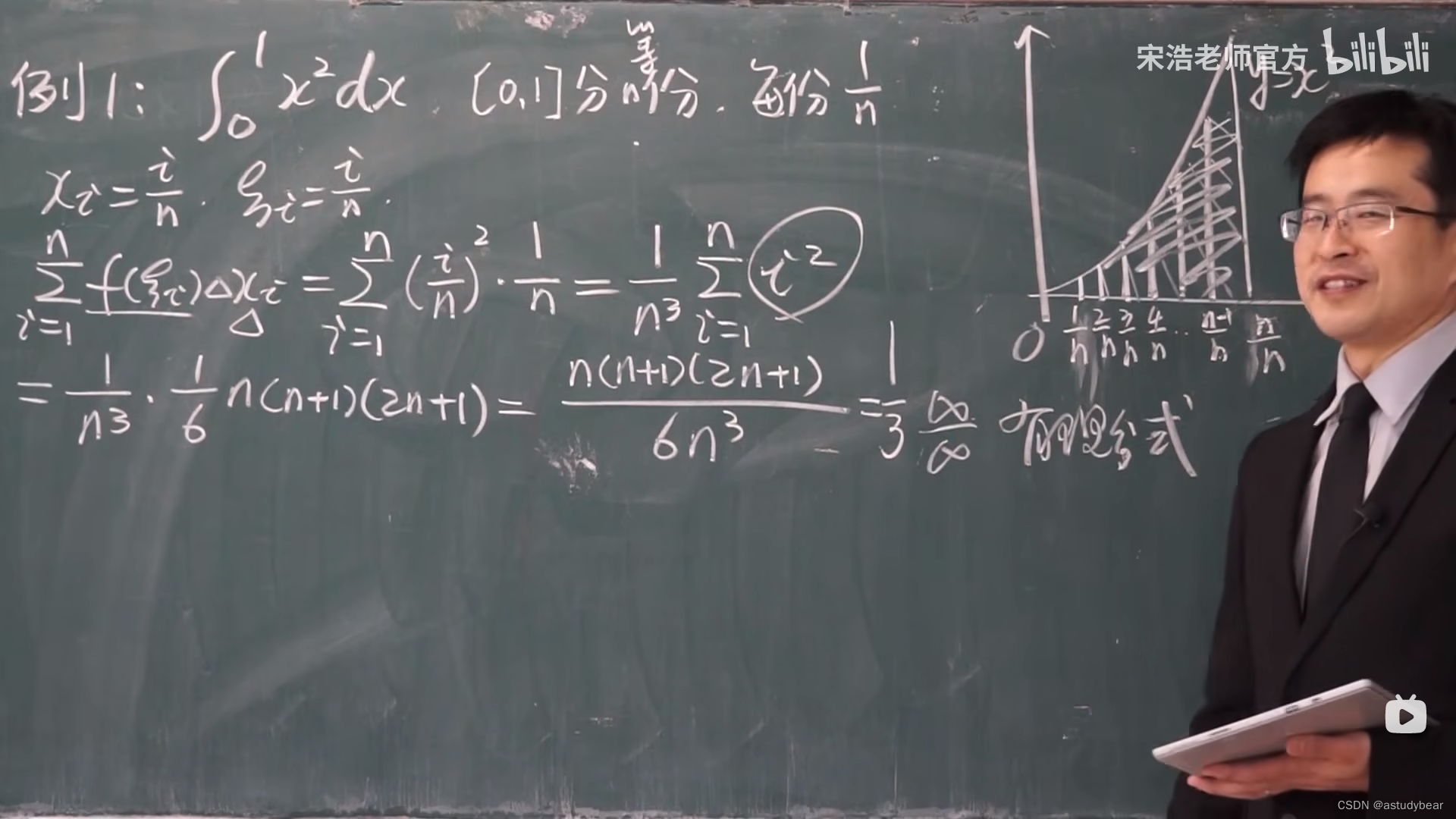
定积分的方法

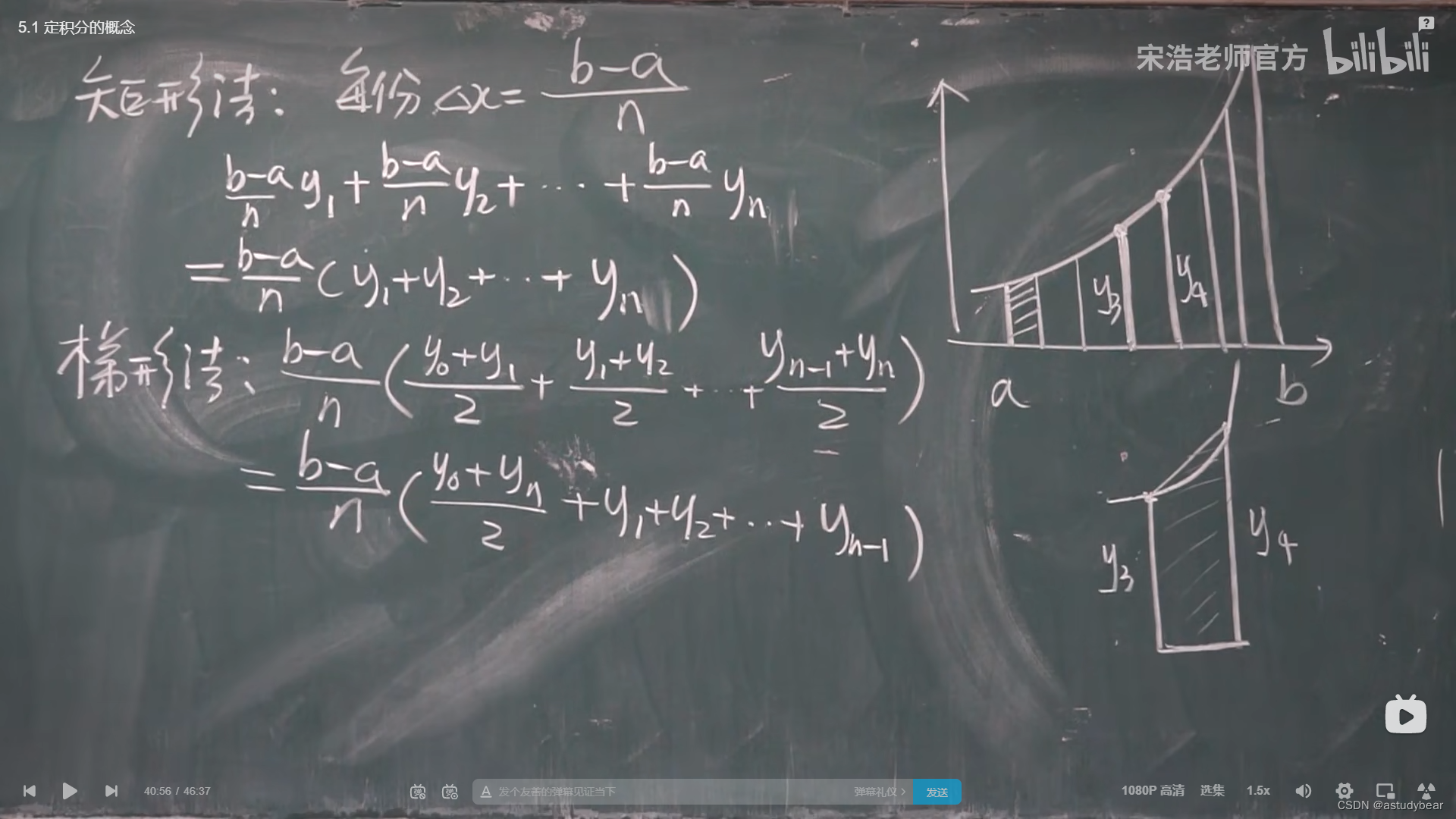
用概念做题比较少，一般都是用下一章的性质来做题 

5.2定积分的性质

 定积分的性质

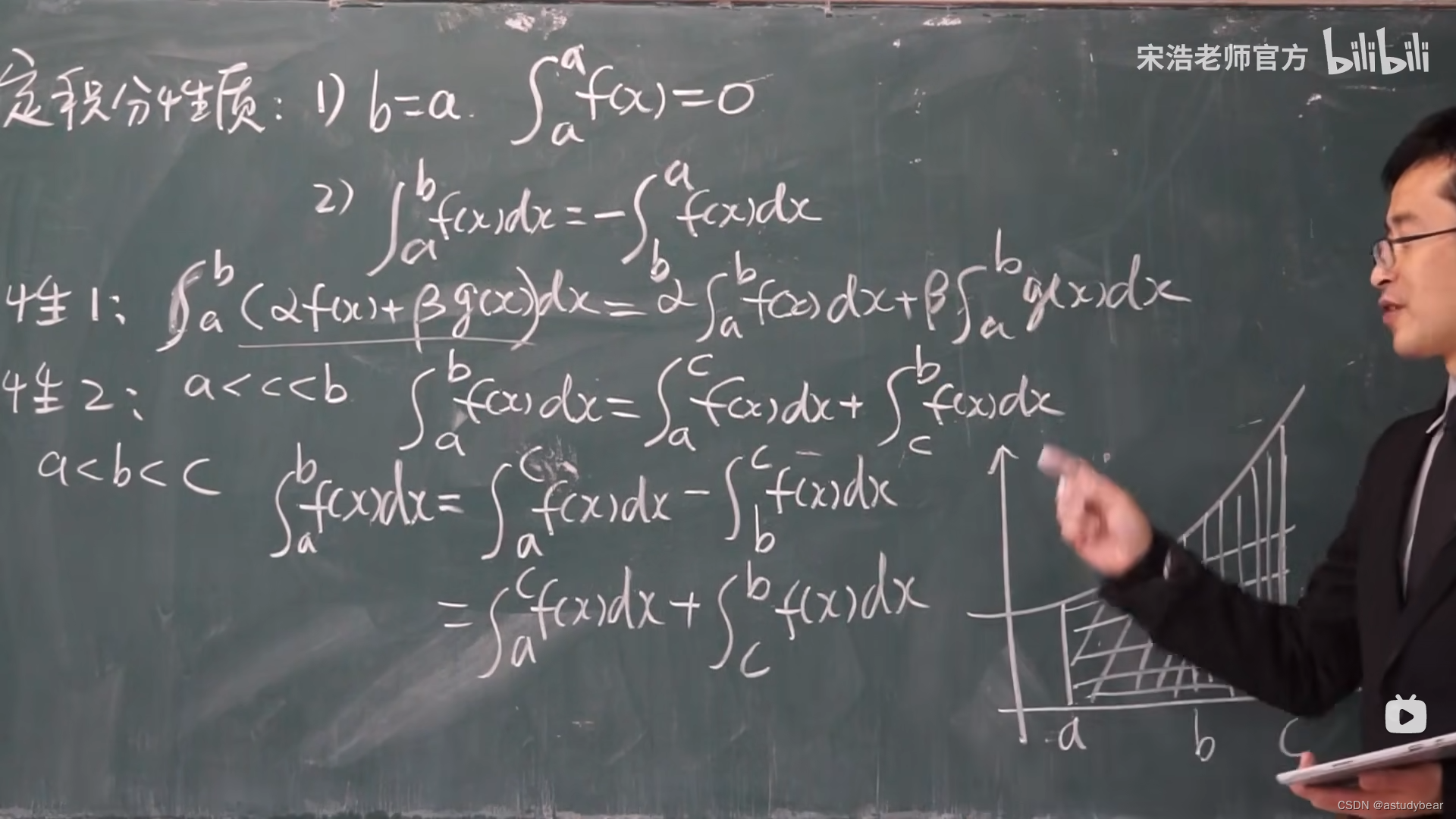
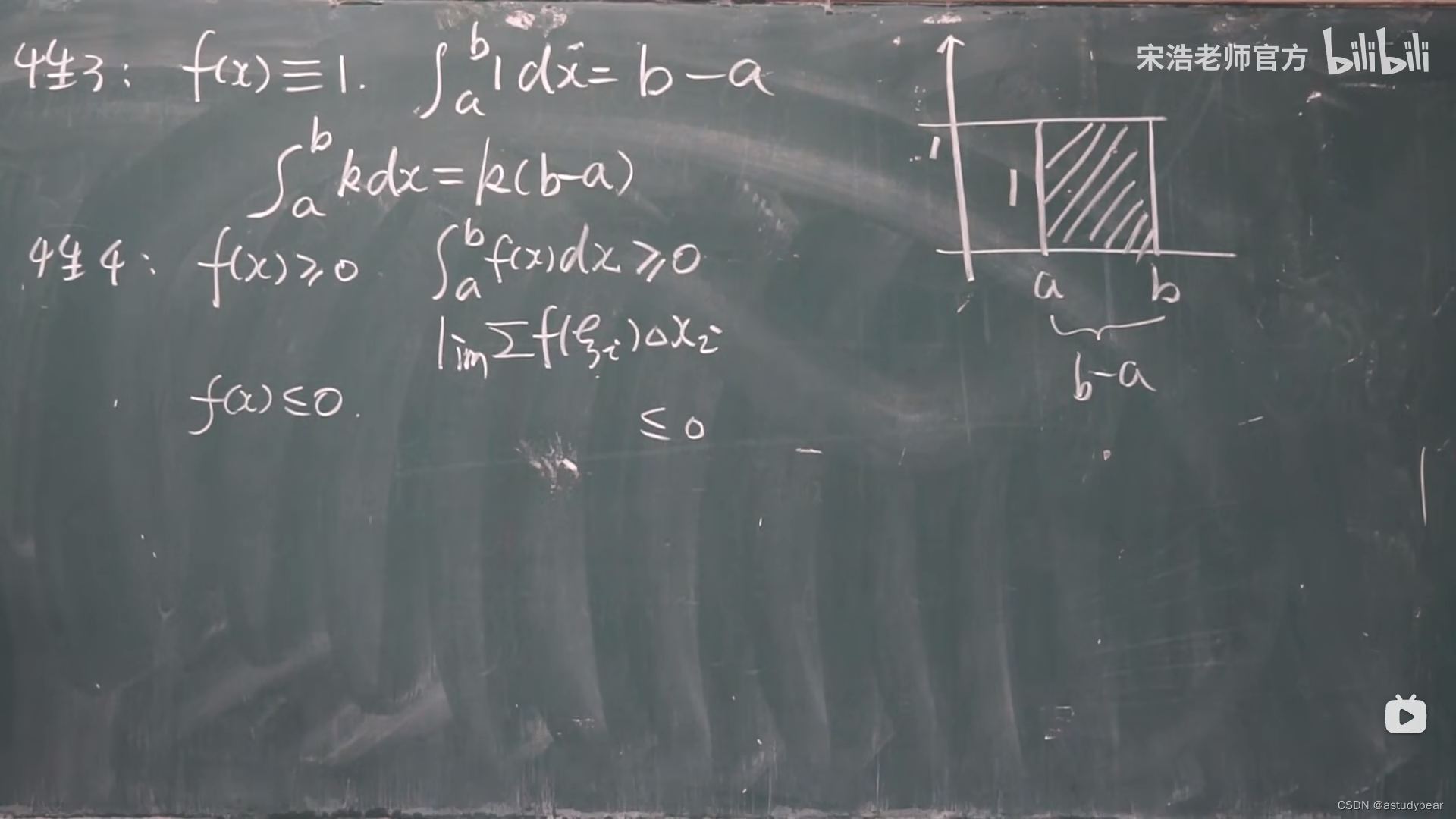
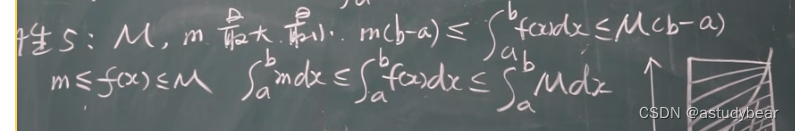
 性质特别重要，考试考定义不多，基本都考的性质！！！！

 定积分的推理：

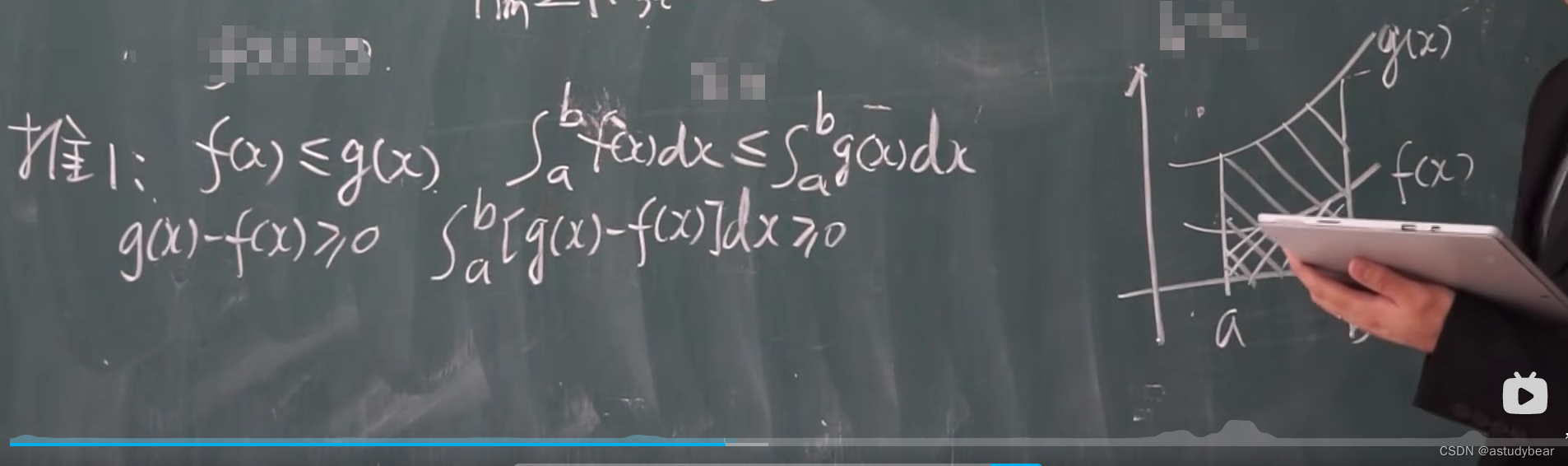
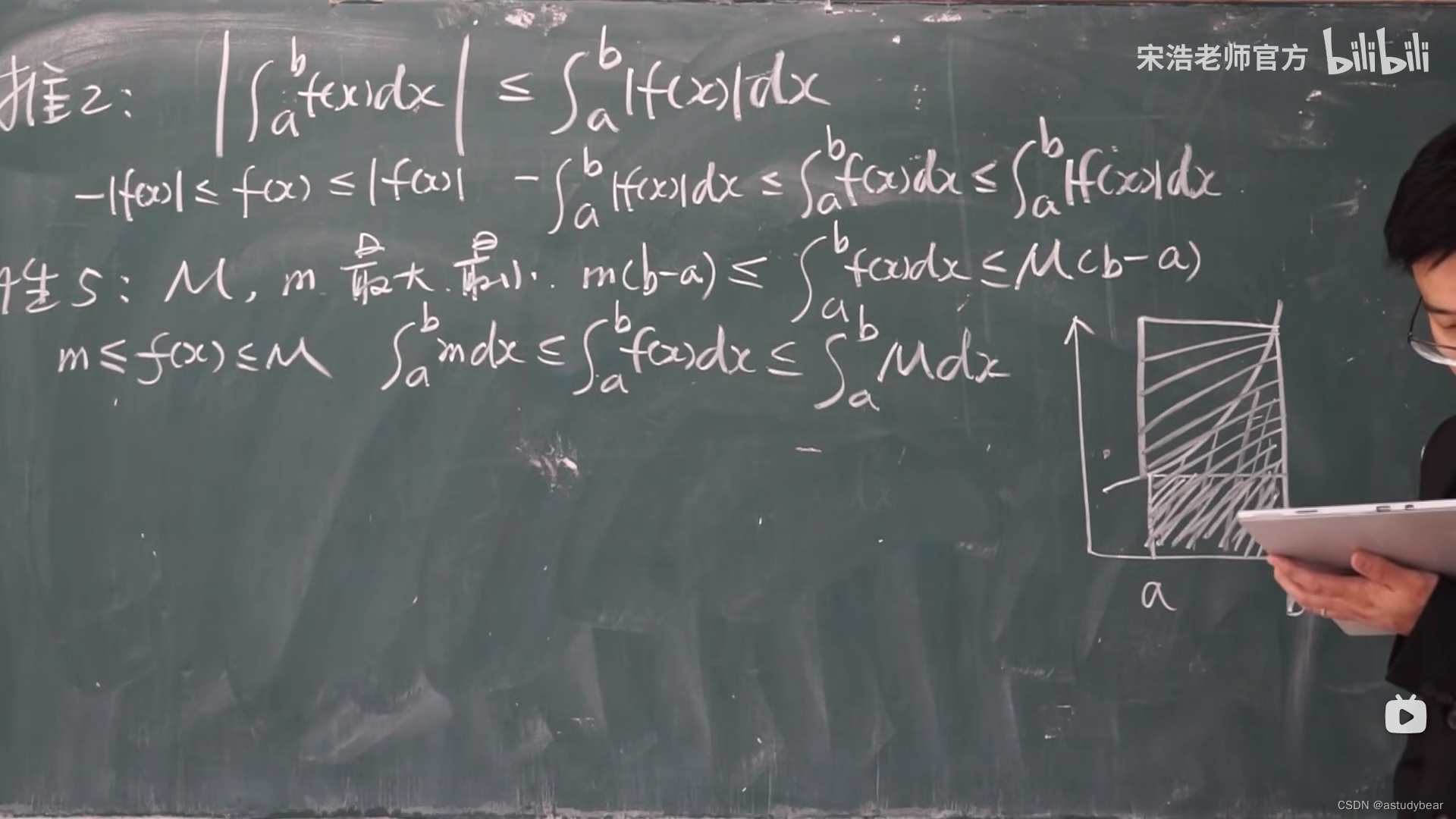
 5.2微积分的基本定理

积分上限函数 

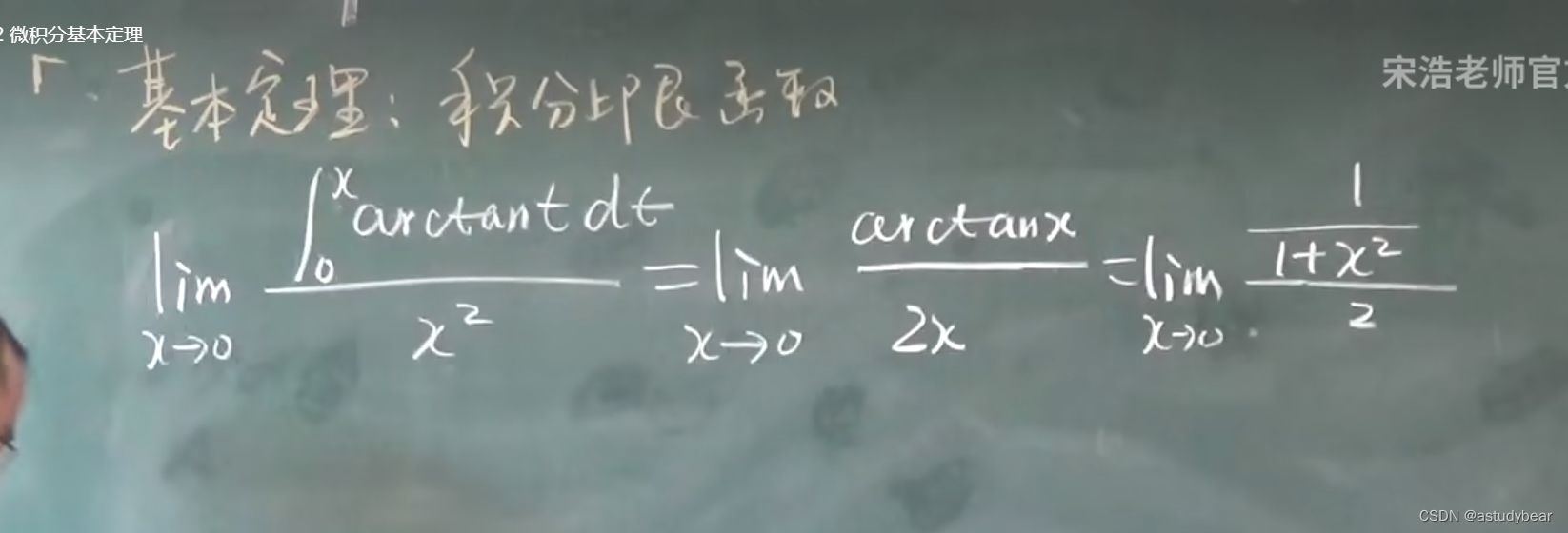
 分段定积分

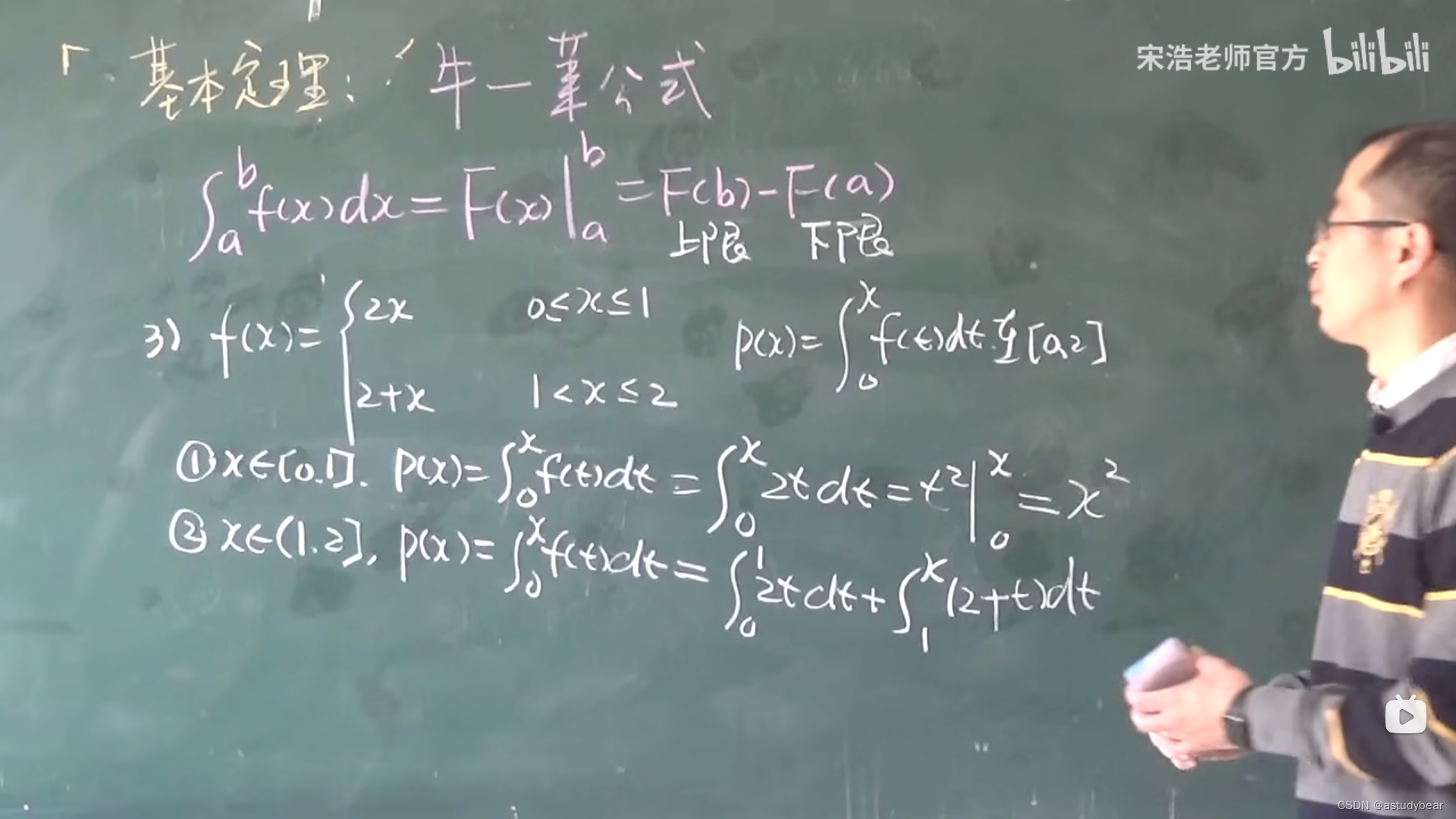
 5.3换元积分法

 思路

定义

 例题：

例一：（两颗星）

 例三：（三颗星）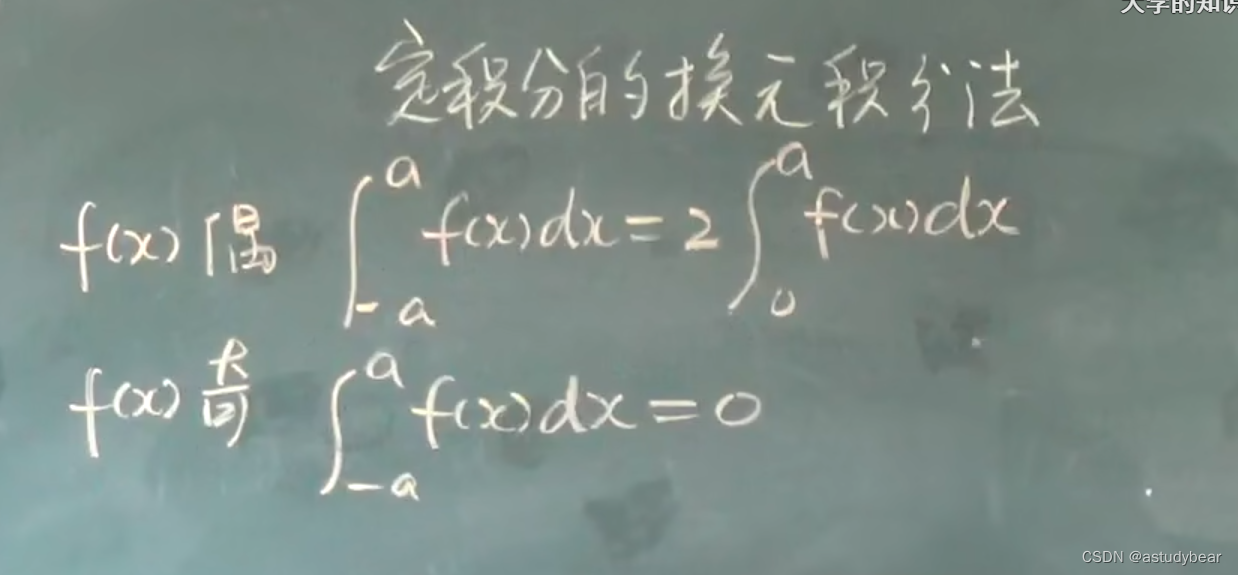

 

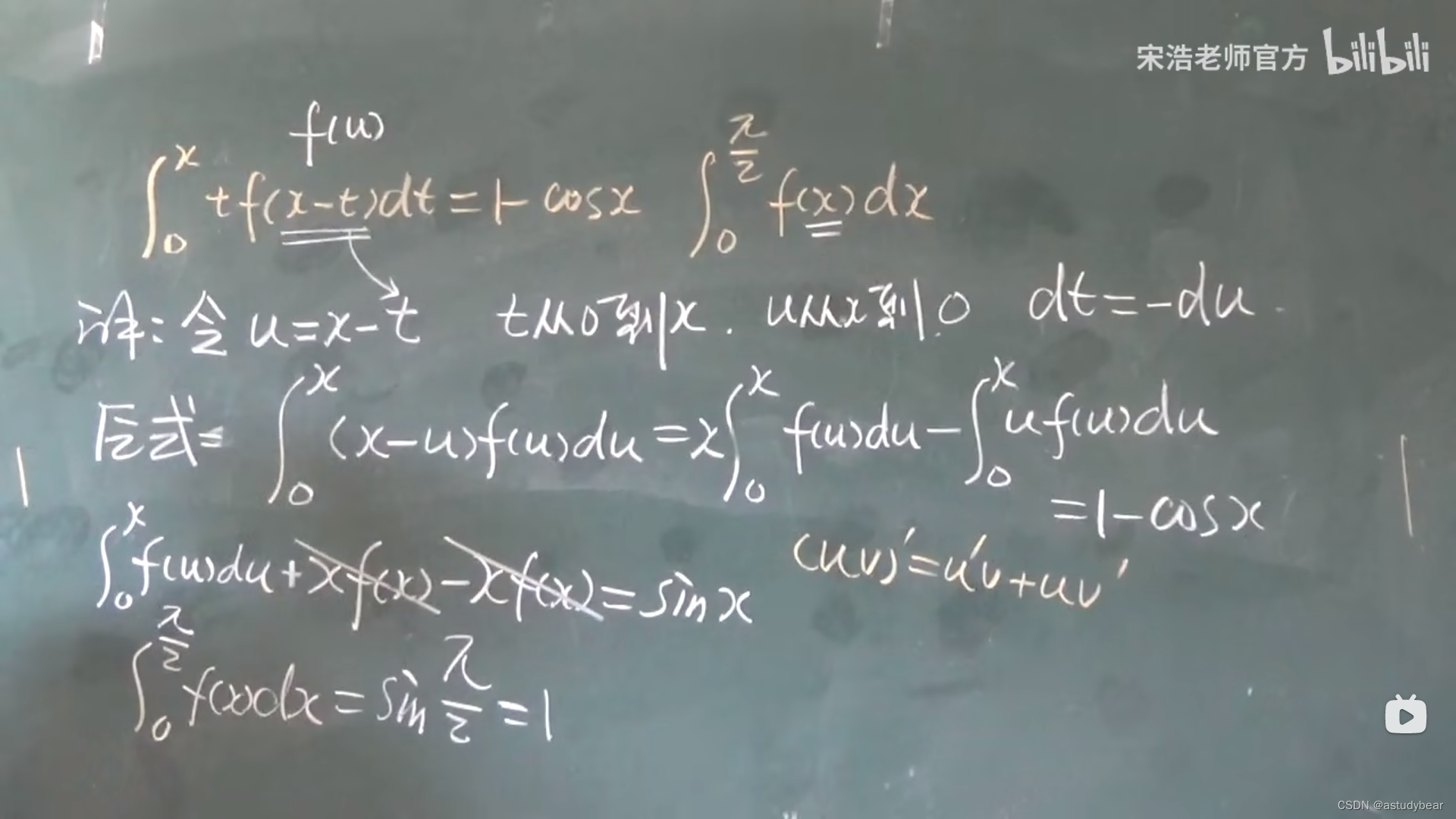 换元积分步骤：

①引入这个换元函数（函数需要单调！）

②引入后积分的上下限也要换

性质三非常重要（上图的例三）！

注意做题的时候画图是最好理解的，就是求他的面积罢了

5.3分部积分法

 定积分和不定积分都是一样的公式

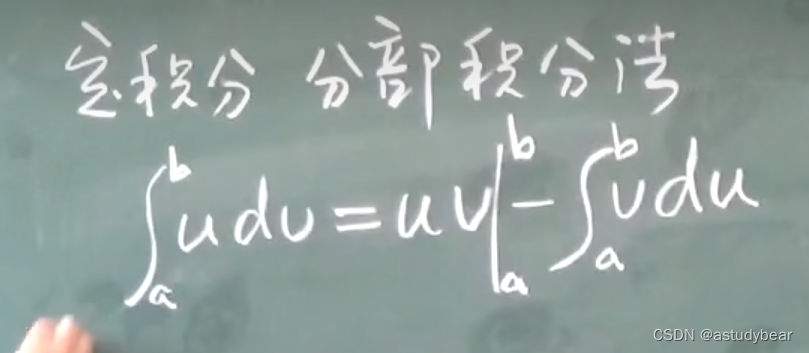
例题2：化简后再用分部积分法就可以了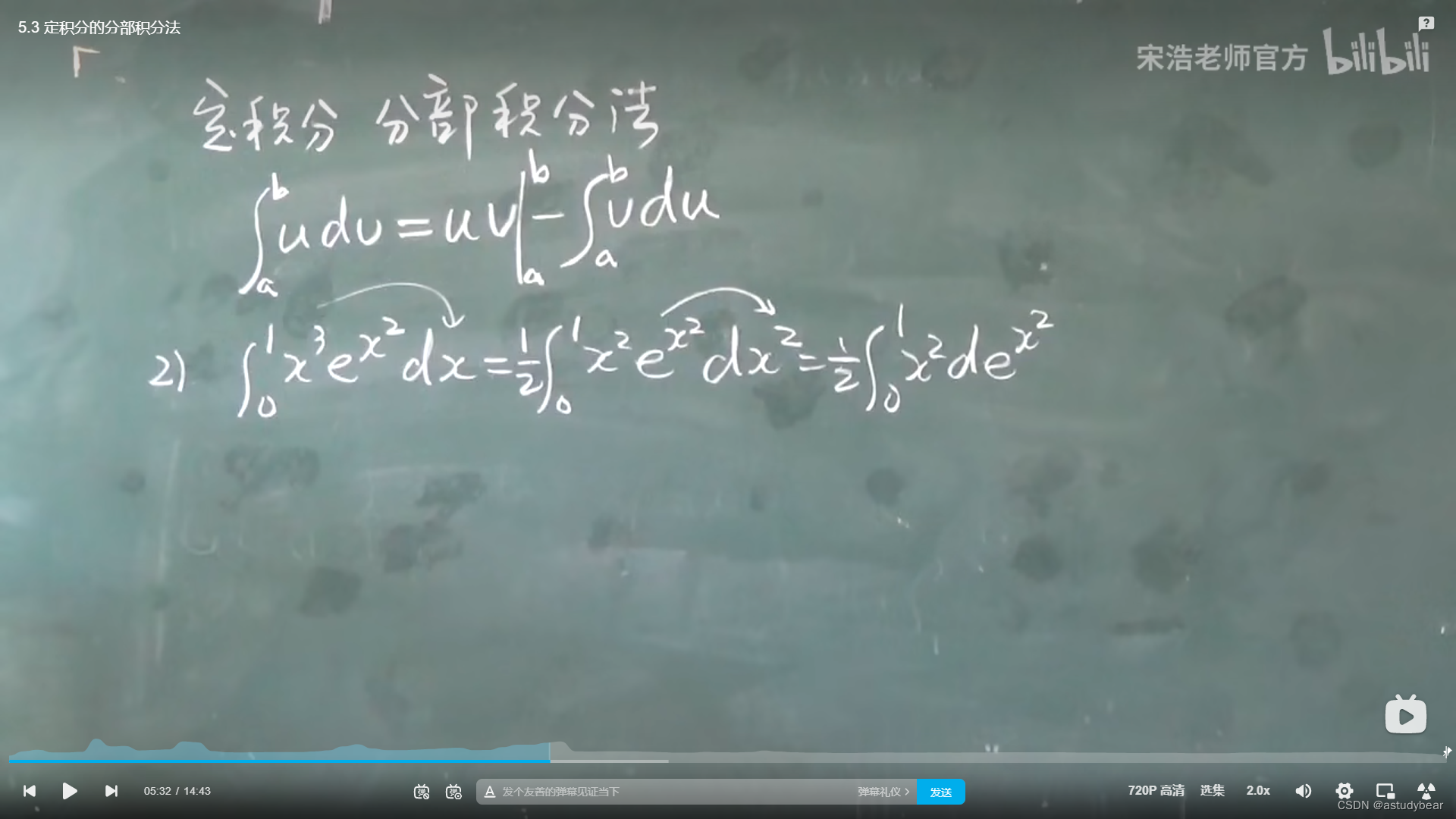

 

5.4定积分的应用-求面积

要么就是上面-下面，要么就是右边-左边 

求面积步骤

①画图

②判断是x、y型（边界垂直于哪个轴就是哪个型）

③解题

        x型：尺子垂直x轴，从最左边开始移动看上边函数是谁、下边函数是谁（分区间），然后就用上边函数减去下边函数。

        y型：尺子垂直于y轴，然后从下到上的移动，判断谁是左边，谁是右边的（分区间），然后把函数表达式改成是x是y的函数。最后就是右边减左边。

5.4定积分应用-求体积 

公式

对他的横截面求导

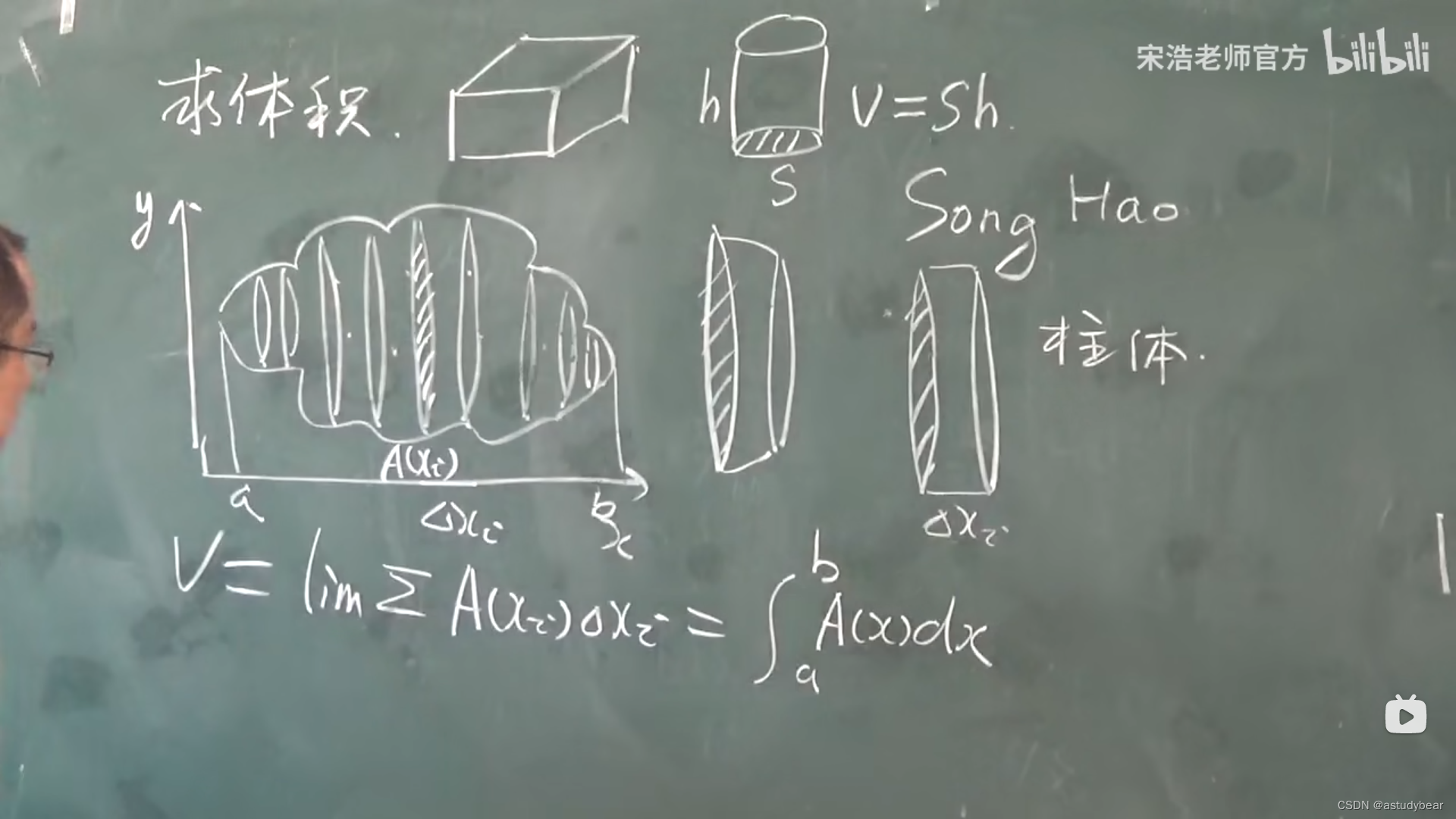
 例题：

①对x旋转，对他的横截面求积分

②对y旋转，对他的横截面求积分，要注意的是一定要把x写成y的函数再带进入求。

题型总结：

第一种：直接求出来

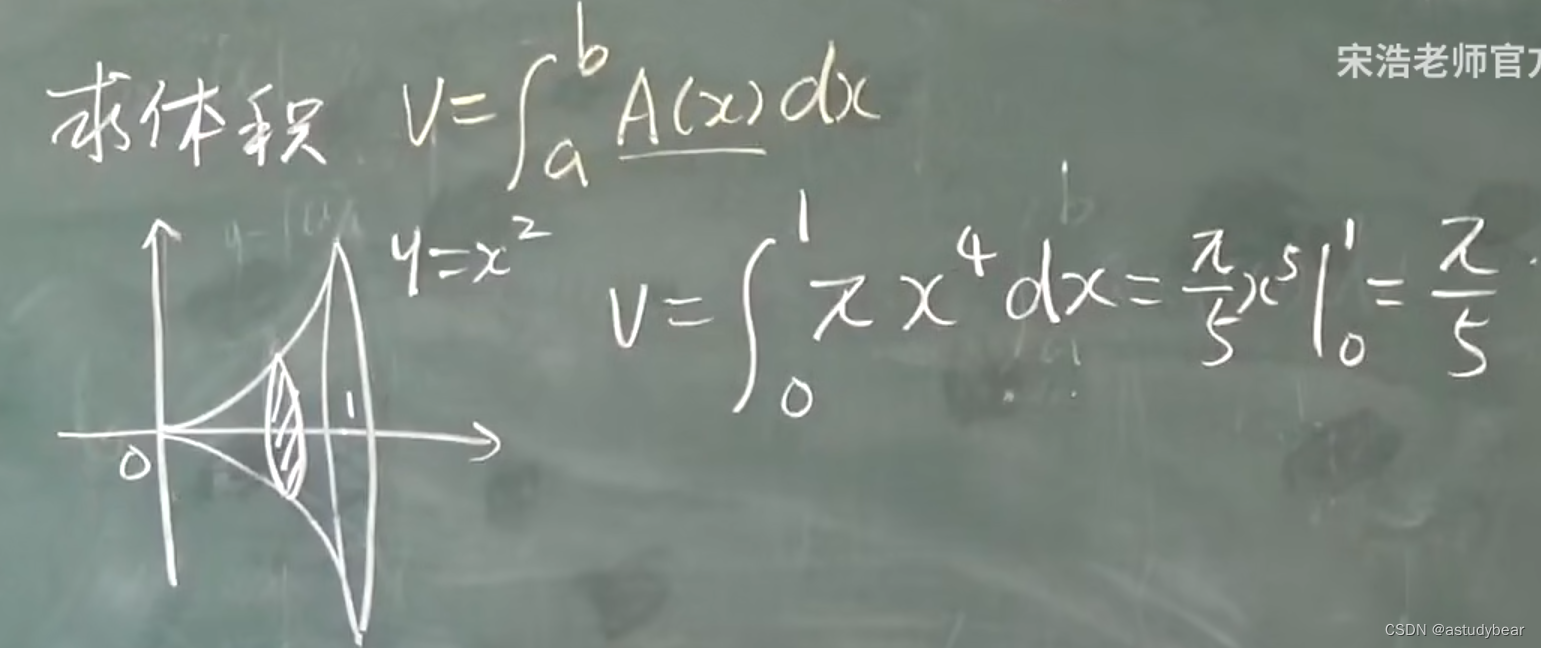
第二种：复合函数形成的图像

        做法一：大圆减小圆，注意！！！要换成x对于y的函数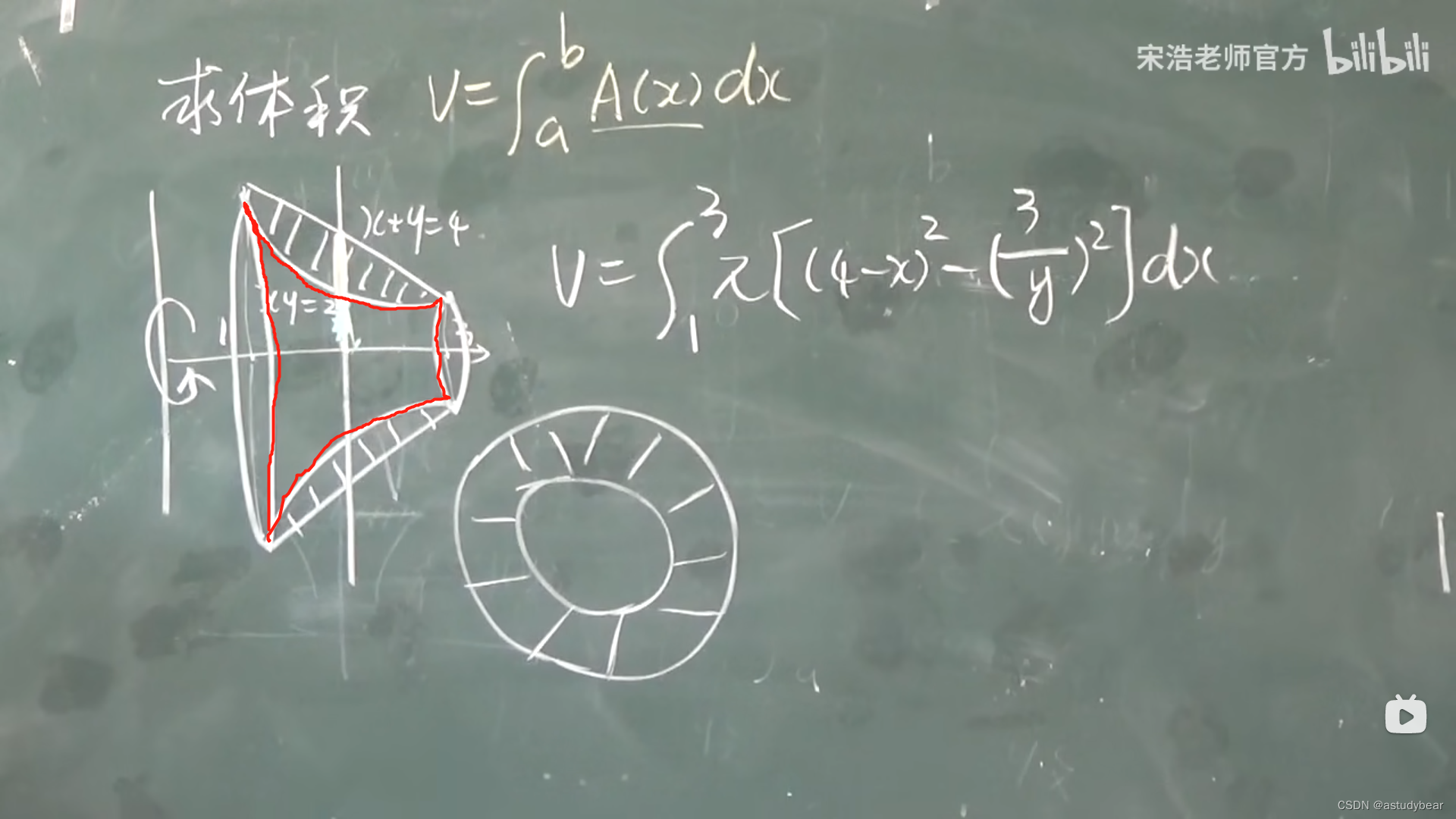

         做法二：一函数的体积减去二函数的体积

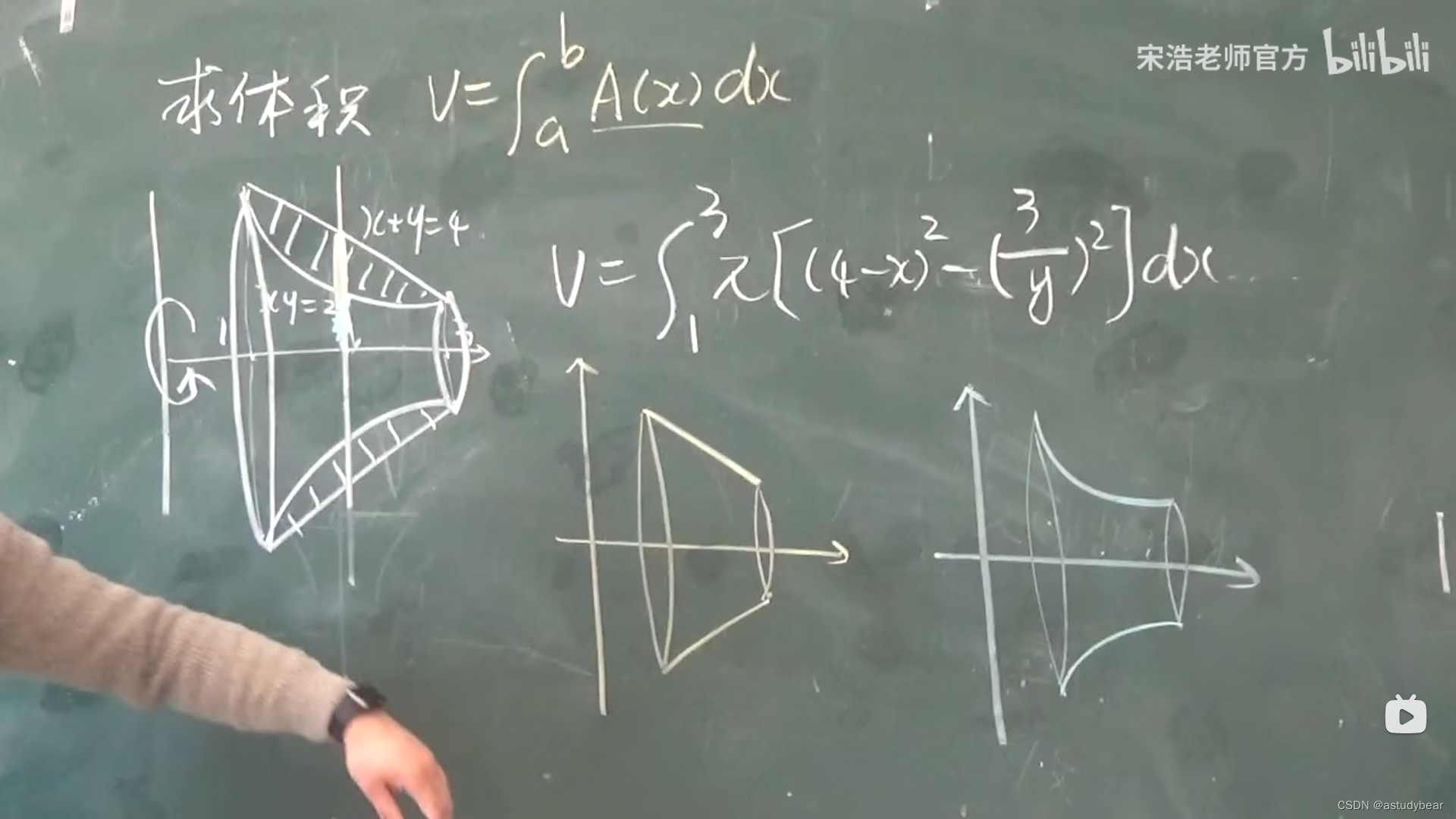
5.4定积分应用-经济问题

 题型一：给你一个变化率，求一段时间的总产量。

题型二：求未来的钱

 题型三：收益问题

公式

 例题：

5.5广义积分-无穷限积分

 例题+推导：

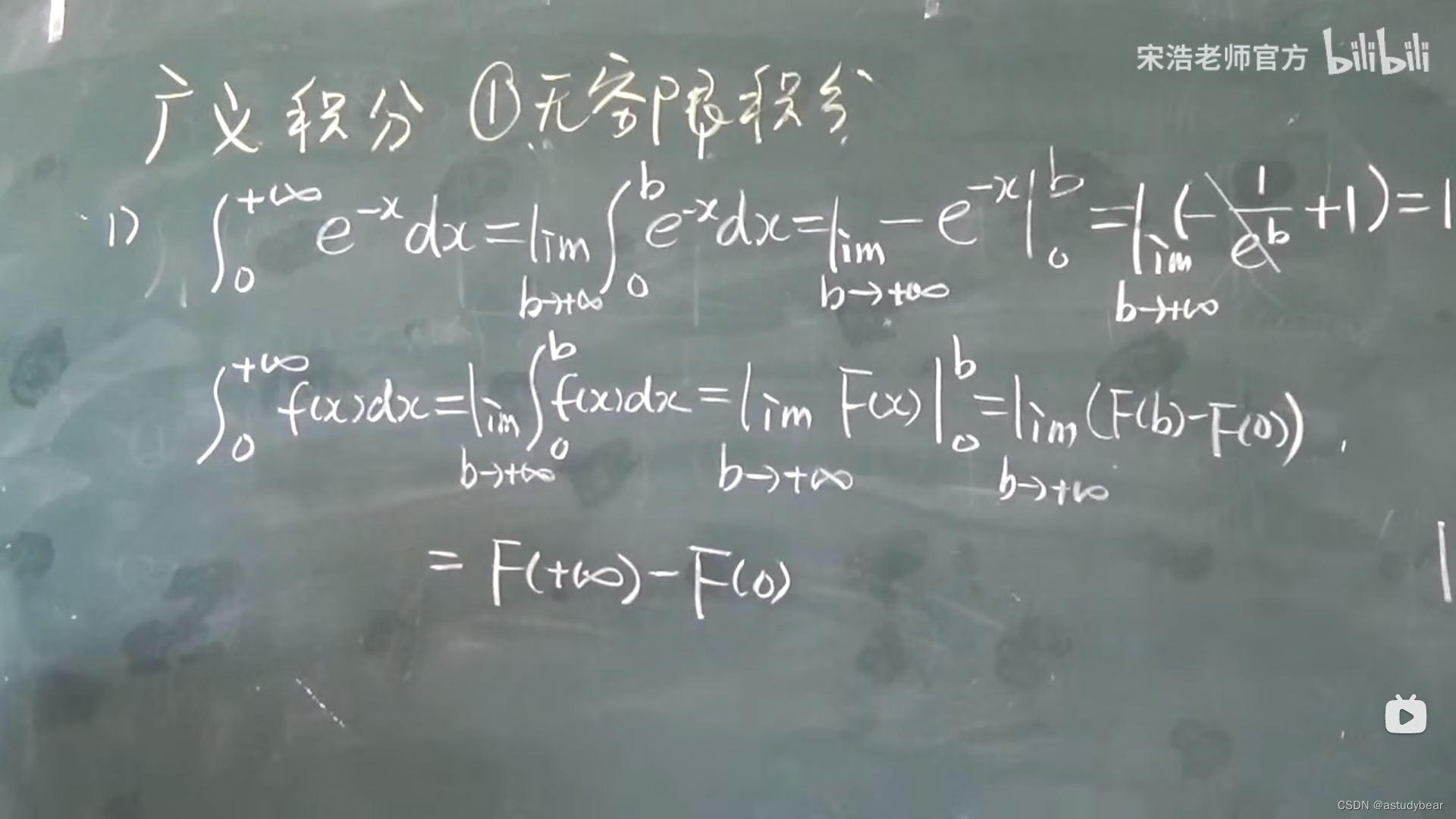
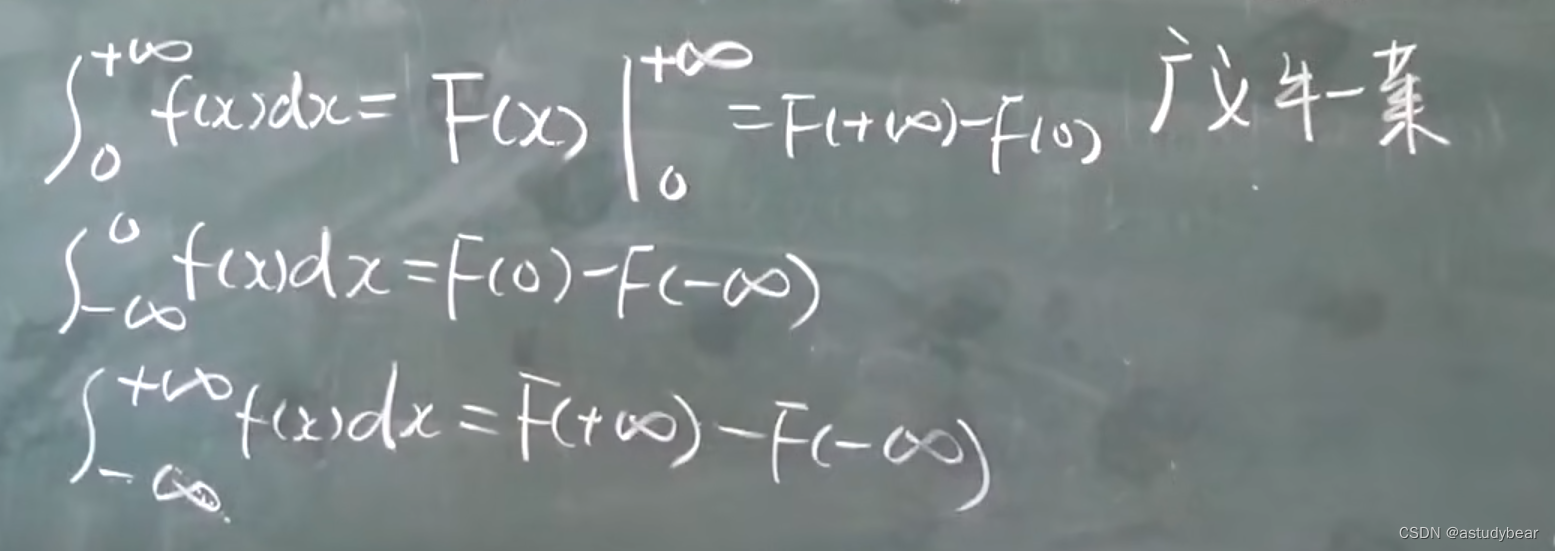
例题：

 无穷定积分的性质：

①f(x)收敛的画，kf(x)也收敛

②f(x)和g(x)都收敛，那么（f(x)+-g(x)）都收敛，反之不可用

③分部积分和换元积分也适用于广义积分

 无穷限积分收敛的判断：

定理1：f(x)>0;收敛的充分必要条件就是F(x)有界

※定理2(比较判别法):

例题：

 

5.5广义积分-瑕积分 

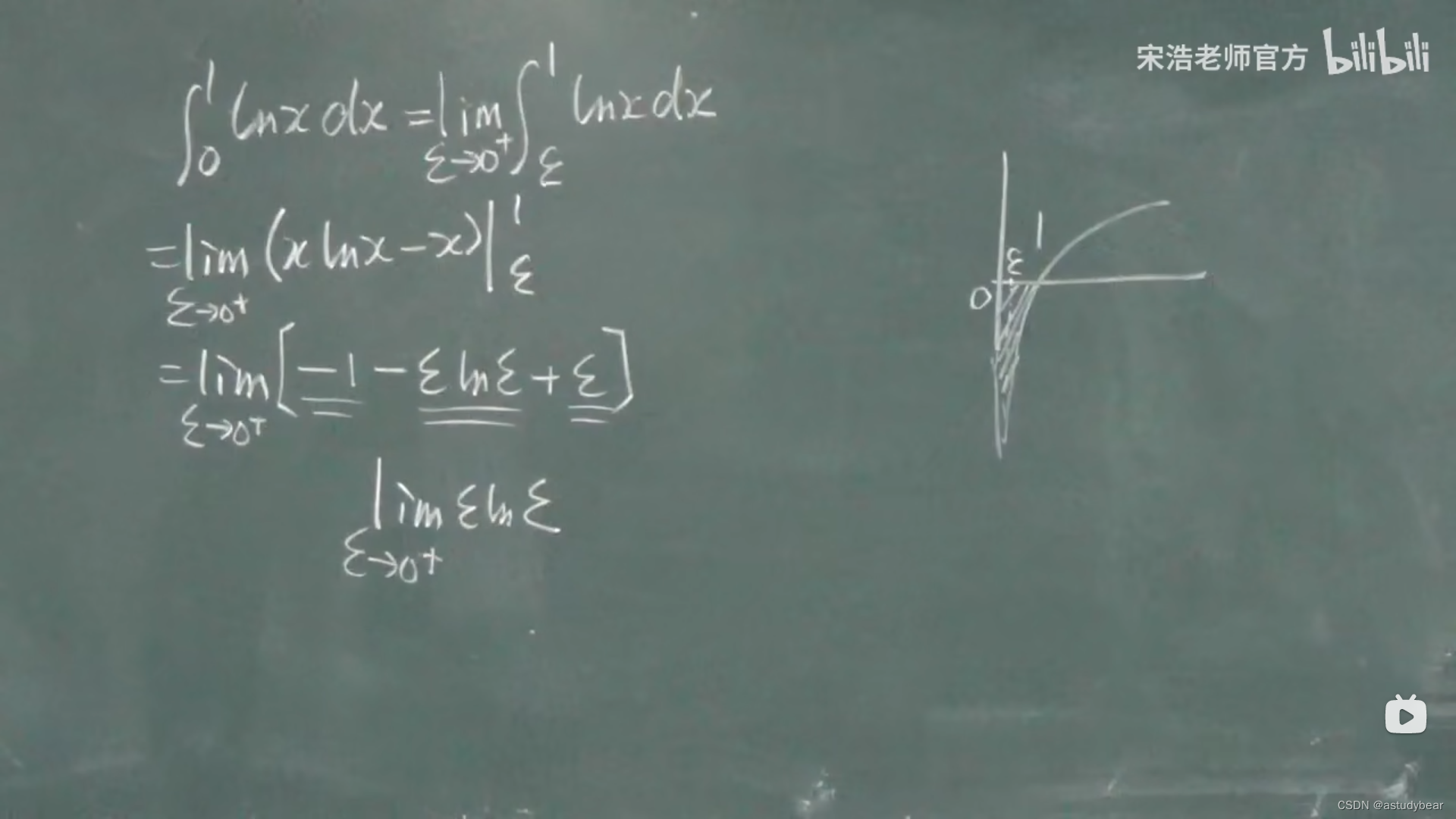
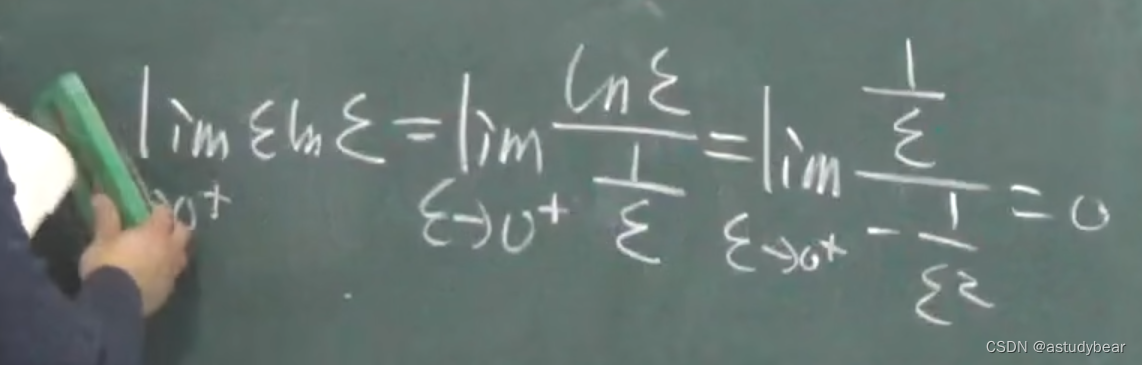 瑕积分也可以用无穷限积分来算，但是瑕积分比较复杂，很少有这种题目

 6.1多元函数微积分

一、基本性质

二元函数就是z关于x和y的函数

定义：

（这章靠最多的就是定义域）

 极限和定义域：

极限就是z一直往z0去靠近，和一元的一样

连续性就是有极限就是连续的

 考点：

 例题：

 二、偏导数与全微分

偏导数（偏向一边的导数）定义：

 偏导数的几何意义以及二阶偏导数：

全微分：

 性质以及多元复合函数的偏导数

隐函数的偏导数：

直接两边求导然后导出来会有一个z·直接提出来就好了

 例题：

三、二元函数的极值 

极值求解步骤：

①先求出一阶偏导数x的和y。然后求出驻点（令x和y的一阶偏导数为0就可以求出驻点）

②求出A、B、C的值然后再把驻点代入，去判断。

 条件极值的求解

例题 ：

 

有条件的极值步骤：

①先把题目给的信息化成两个式子，一个化成条件，一个化成问题

②代入拉格朗日公式，条件放右边并且前面带λ，然后问题放左边。

③求驻点，在拉格朗日公式分别求x、y、λ、z的偏导另其等于0。

④如下图步骤

如何去判断连续性，就是你任意一种向这个点逼近的方式，他的极限都存在且相等！

 偏导和连续的区别就是连续比偏导严格

偏导是x和y方向连续，而连续是各个方向都一样

二重积分

要求：

二重积分的几何意义：

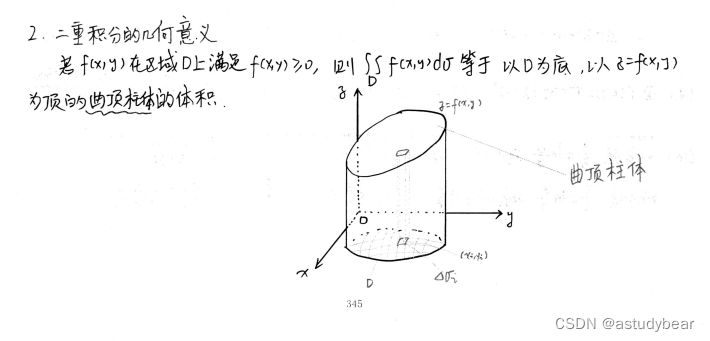
二重积分的性质：

例题：

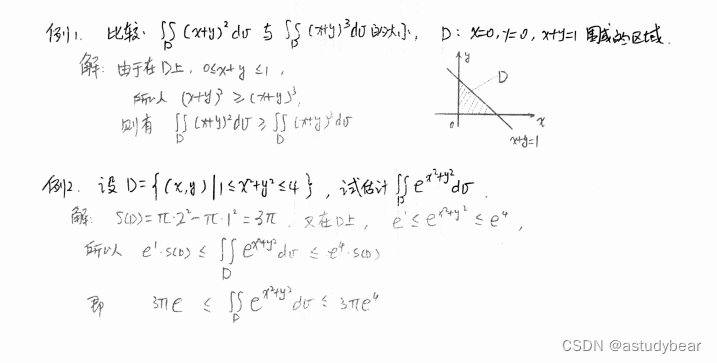
 二重积分的计算：

直角坐标的计算：

公式：

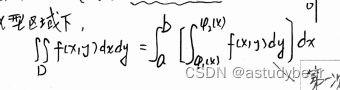
分为y型和x型以边缘垂直于哪边区分，

 极坐标系：

复习一下极坐标的概念

极坐标是以θ和r来表示一个点的，θ是图像在坐标系的哪里，r是点离远点的多少，

而 x=rcosθ，y=rsinθ。

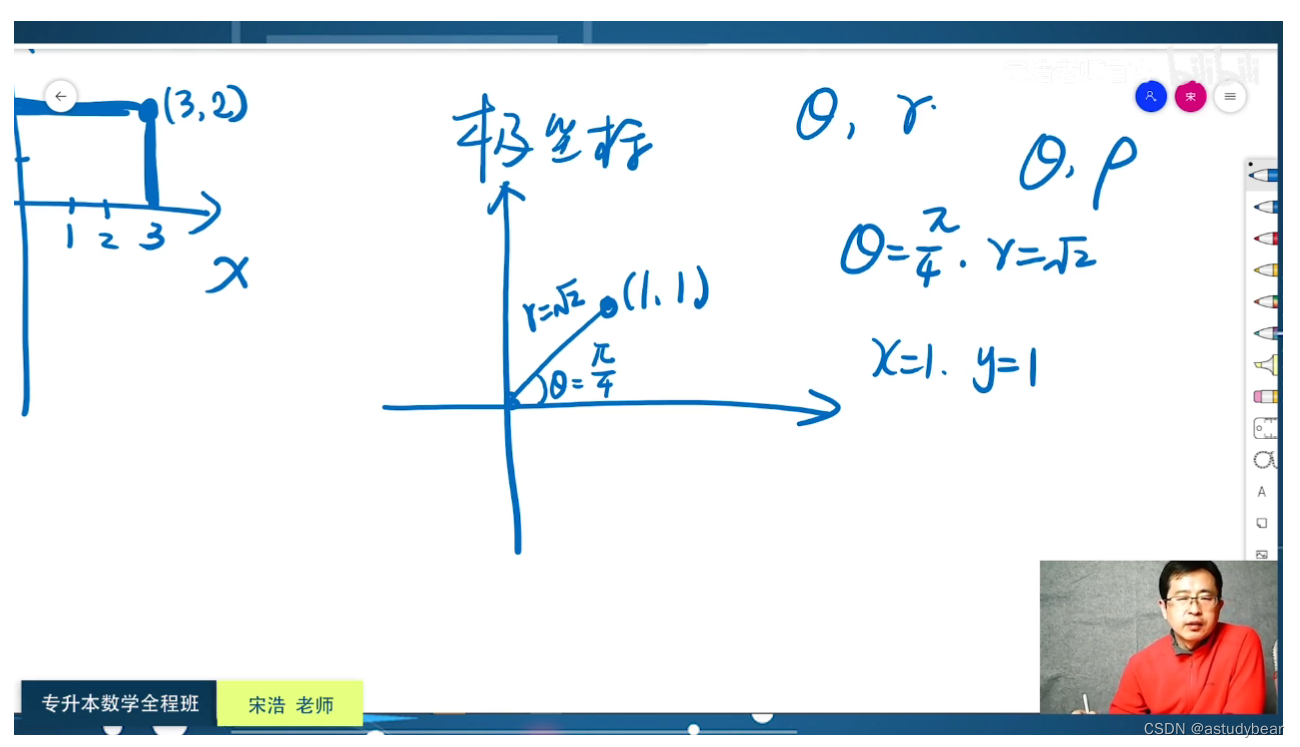
极坐标求值：

①先求θ和r的取值

②前面最外层的上下限是θ的范围，里面的是r的上下限范围，然后r里面的函数要平白无故的乘以一个r，例子如下：

第七章 无穷级数

无穷级数的概念和性质

概念：无穷的“数列”

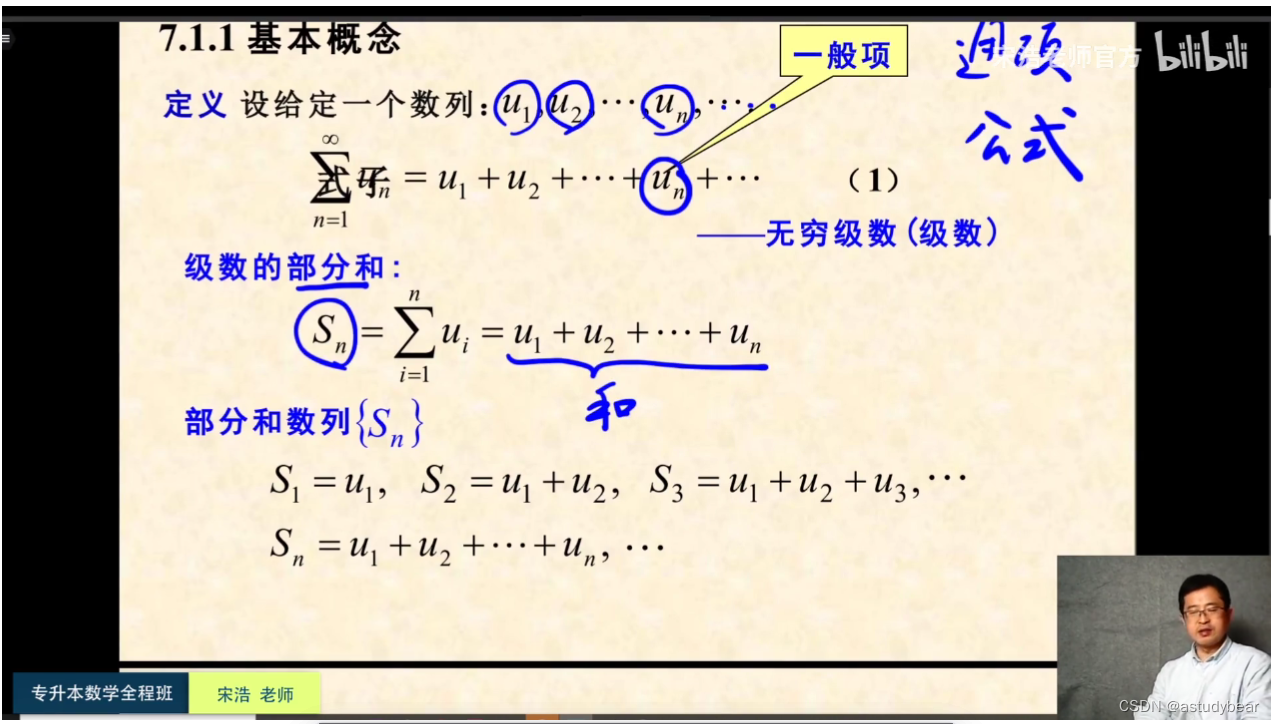
级数收敛：

 等比级数：

|q|<1收敛

 无穷级数的性质：

 

 

 如果级数收敛，那他的通项一定趋于零，但他不能通过通项趋于零来判断。

做题技巧： 

级数的收敛、发散的判别法

如何判断收敛或发散（仅适用于正项级数）

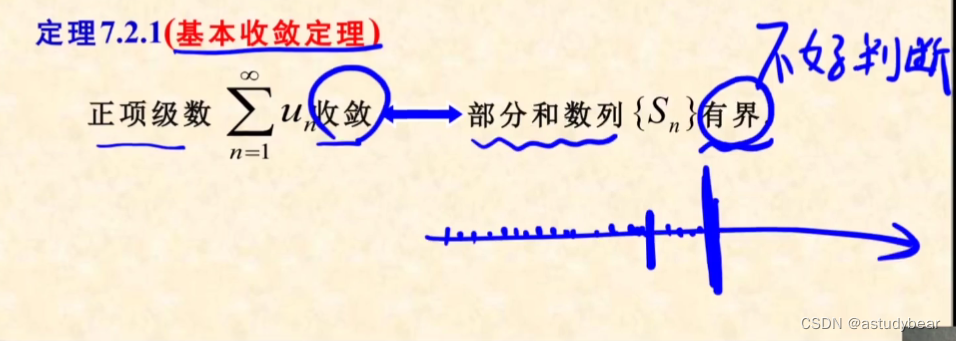
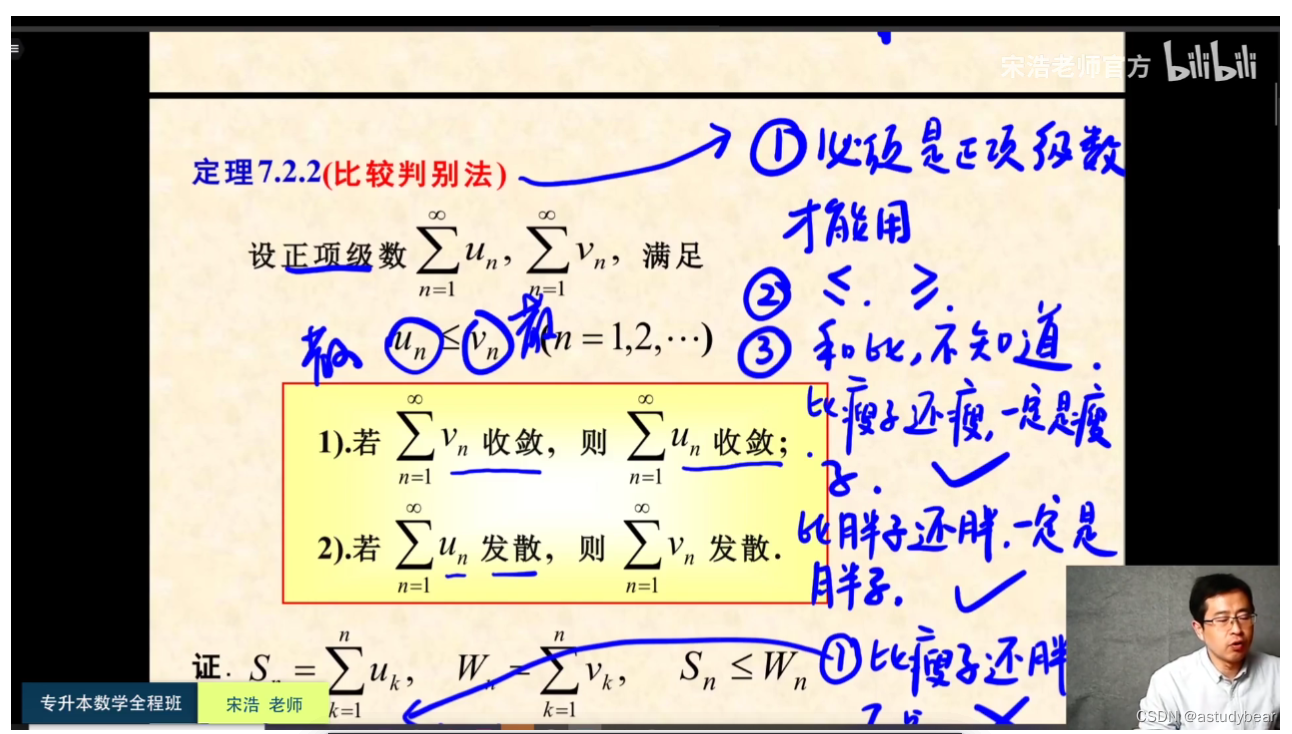
重要！！！比较判别法的极限方式！！

 

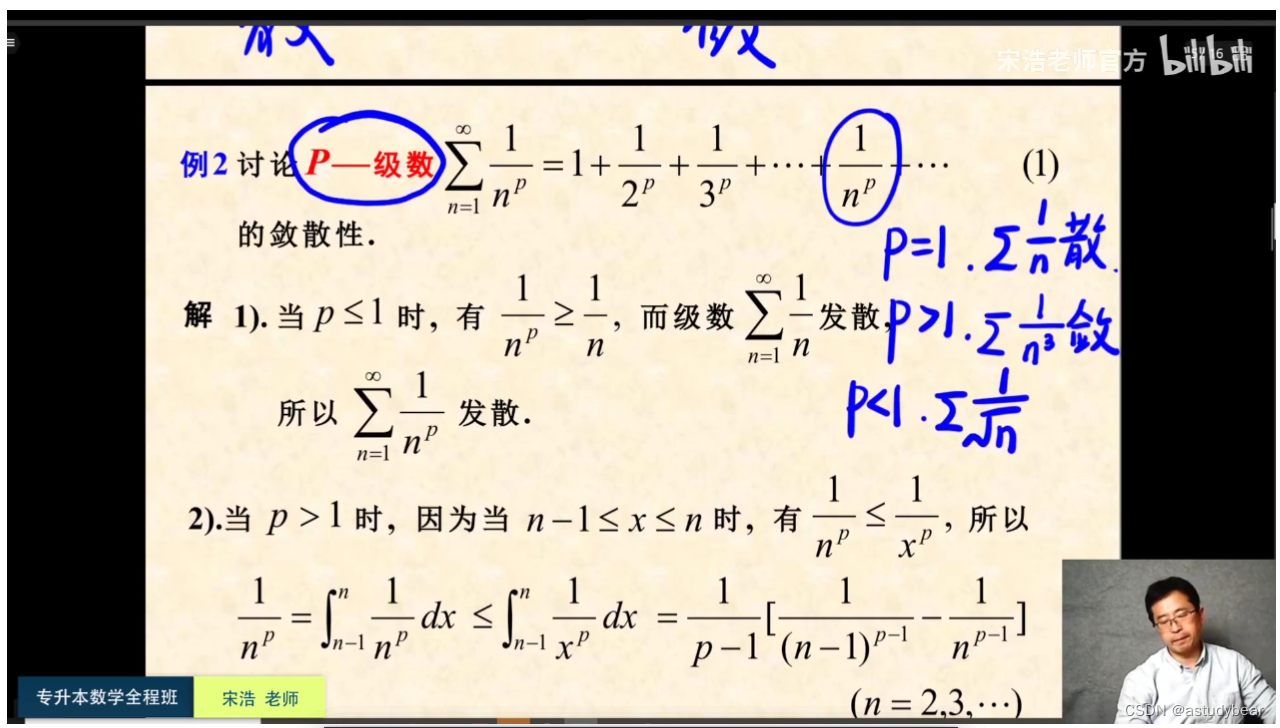
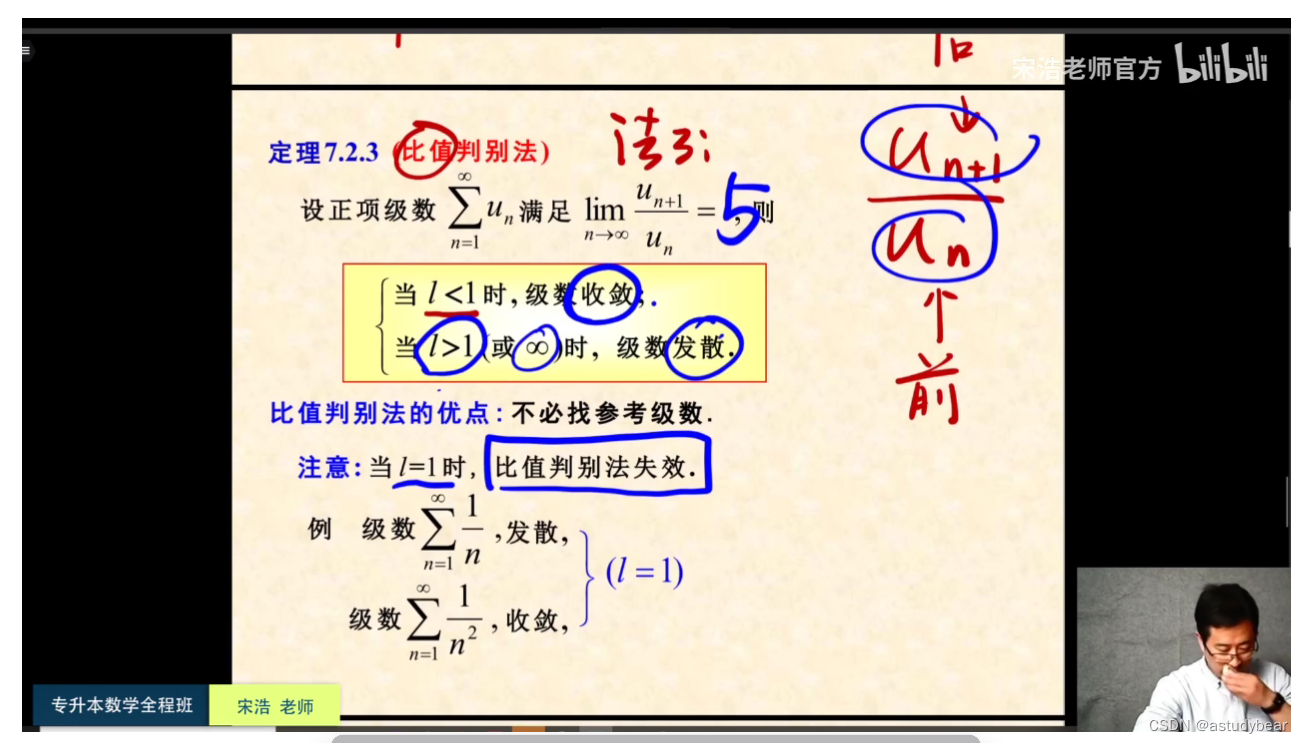
总结：

任意项级数

定理：

交错级数的收敛条件：

 任意项级数转化成正项级数的话，若正项级数收敛，任意项级数也收敛。

  性质：

 小结：

幂级数

本章节的考试题型为：求收敛域或收敛半径以及端点是否可包含，和函数 

概念：

函数项级数：每一项即与n有关也与x有关。

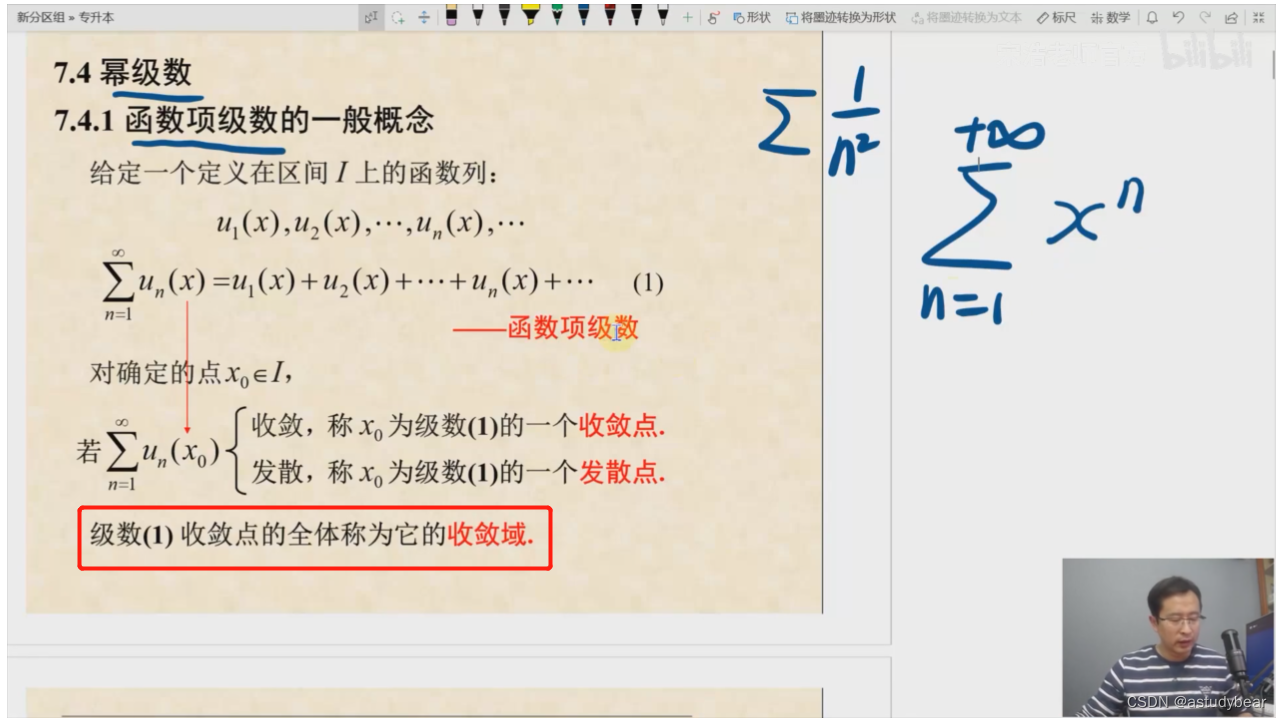这一节主要解决两个问题就是收敛域和和函数

解题：

和函数的求法：

 收敛半径的求法：

注意！！！！用这个求收敛半径他的an是前面的系数！！！！是系数比！！！如果只有奇数项的话就不能用这个！看下面的例题就是没有奇数项的求法！！

幂级数就是先求他的收敛半径，然后将收敛半径的端点代入依次判断，如果端点收敛的话，那就收敛域也包含端点，否则就不包含，然后求出他的收敛域。

例题：

 

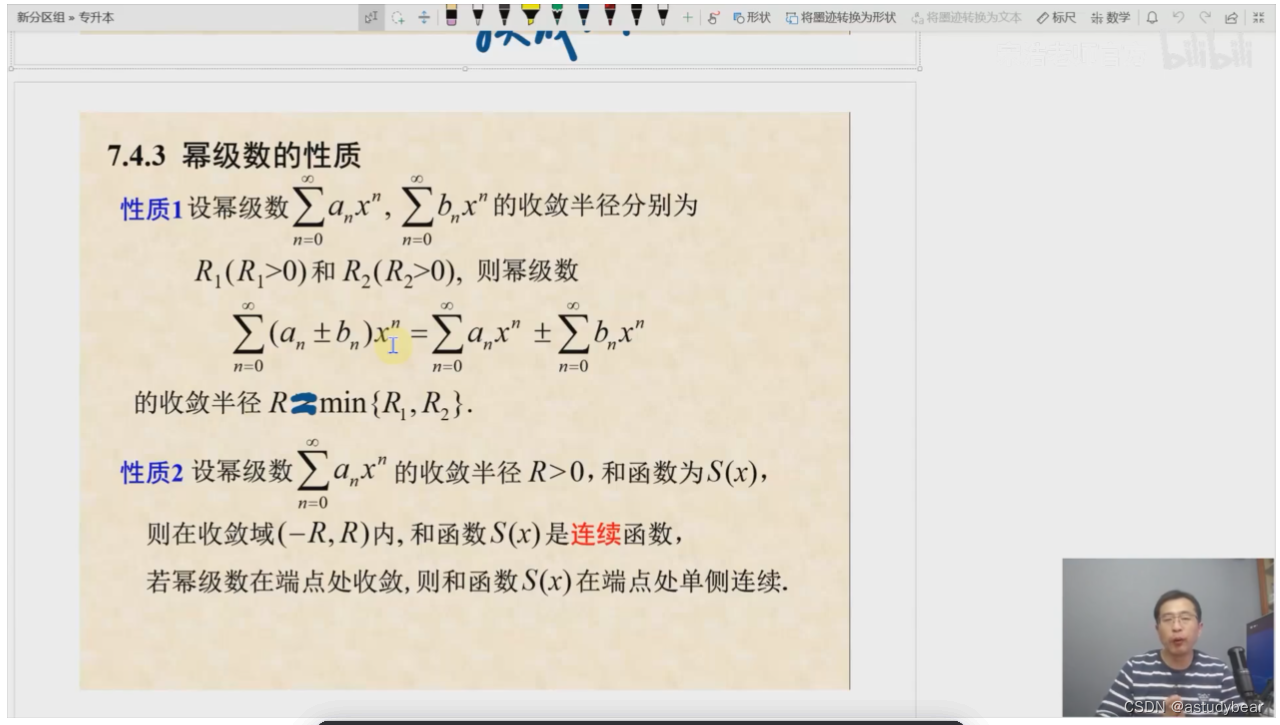
 性质：

1、3、4重要

性质一：a和b相加求和等于分开求和再相加减，然后他们的收敛半径就是两者的最大范围

性质三：对和函数求导=对每个函数求和再求导=先对每个函数求导再求和

性质四：对和函数求积分=先求和再求积分=先求积分再求和（0到x）

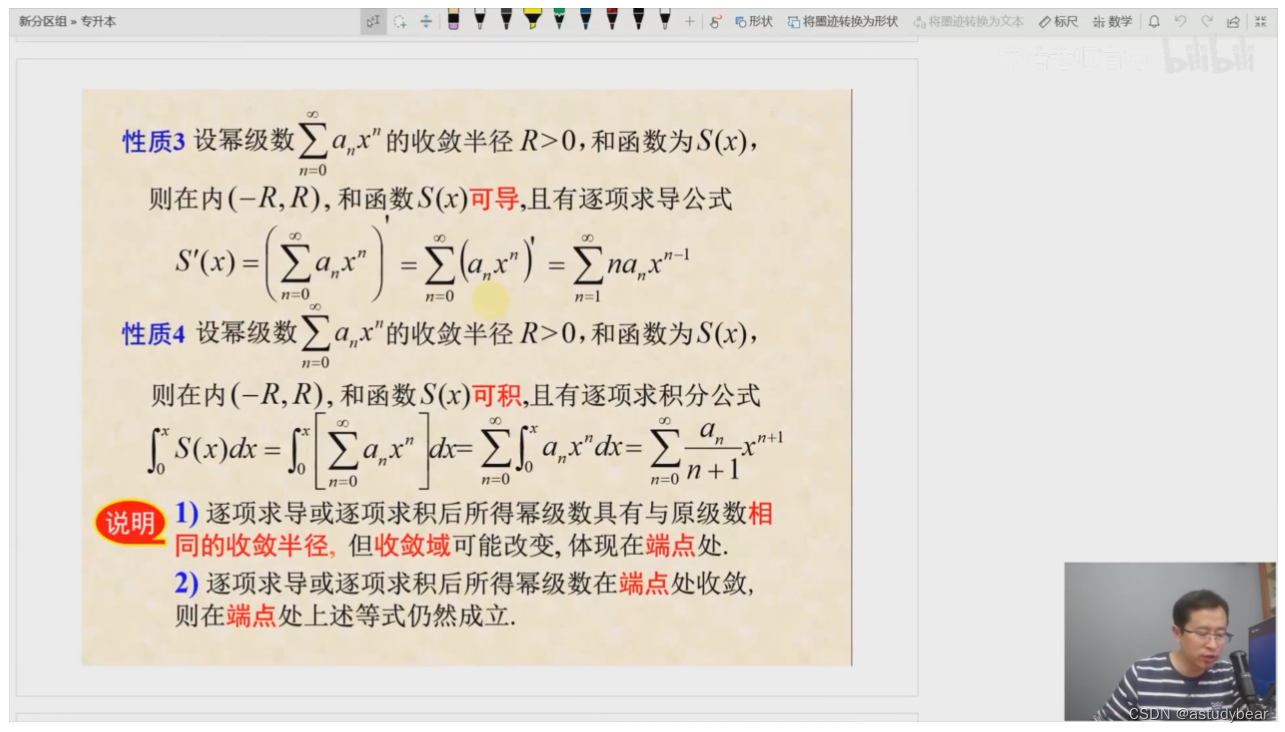
求和函数的两种题型：

首先我们会求的东西只有xn这个等比数列。那么我们就得要转换了，没有就去造，通过求导和积分造出来。

①先求导然后再求积分

②先求积分在求导

例题：

函数的幂级数展开

 

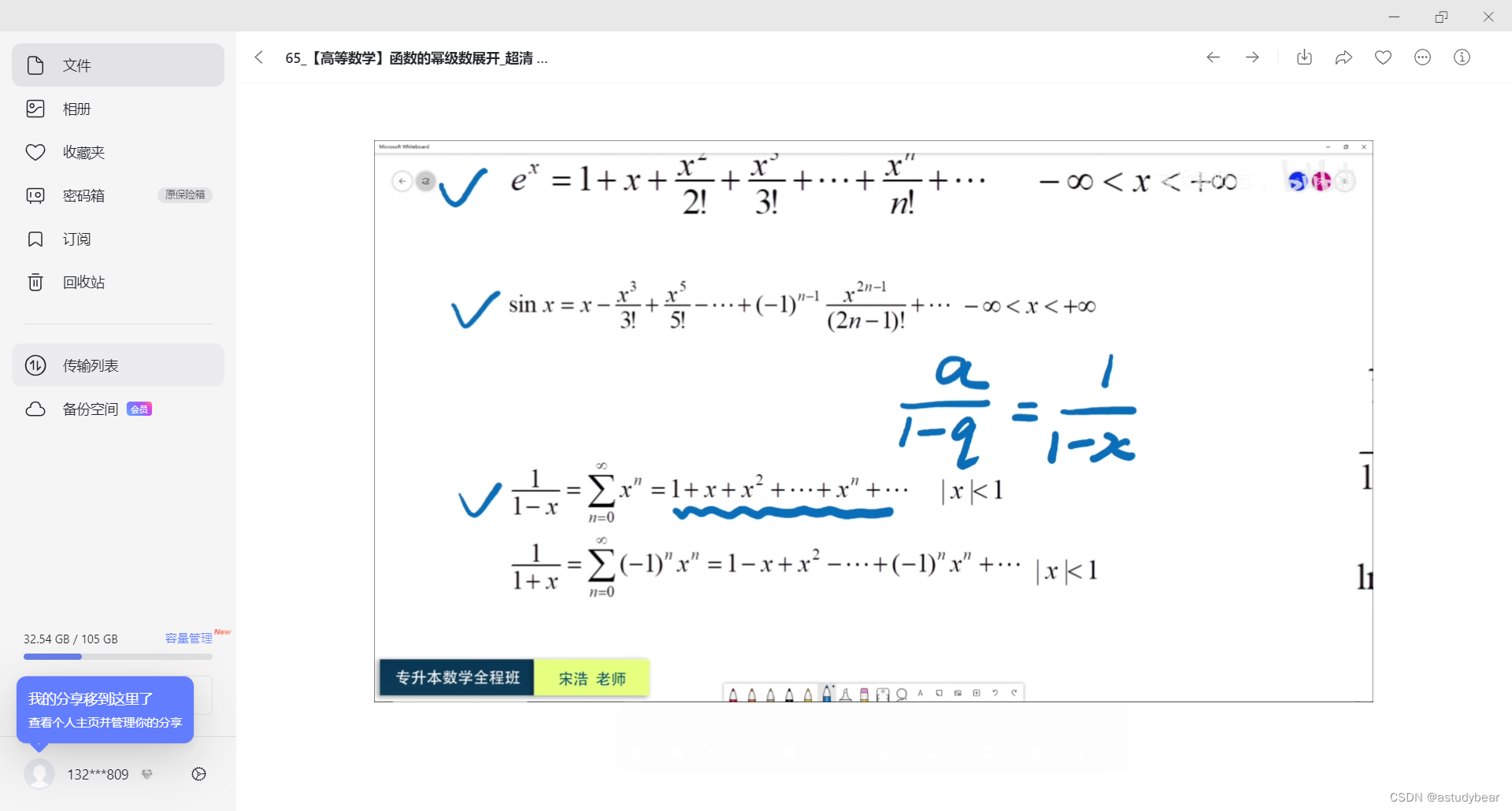
该部分考型是通过基本公式去替换。