一. 题目描述

员工是否准备离职是困扰用人单位的问题，其关系到单位业务的开展及新人员的招聘，及时的分析出有离职倾向的员工成为关键的因素。数据主要包括影响员工离职的各种因素（工资、出差、工作环境满意度、工作投入度、是否加班、是否升职、工资提升比例等）以及员工是否已经离职的对应记录。

二. 数据说明

数据分为训练数据和测试数据，分别保存在pfm_train.csv和pfm_test.csv两个文件中。 其中训练数据主要包括1100条记录，31个字段，主要字段说明如下：

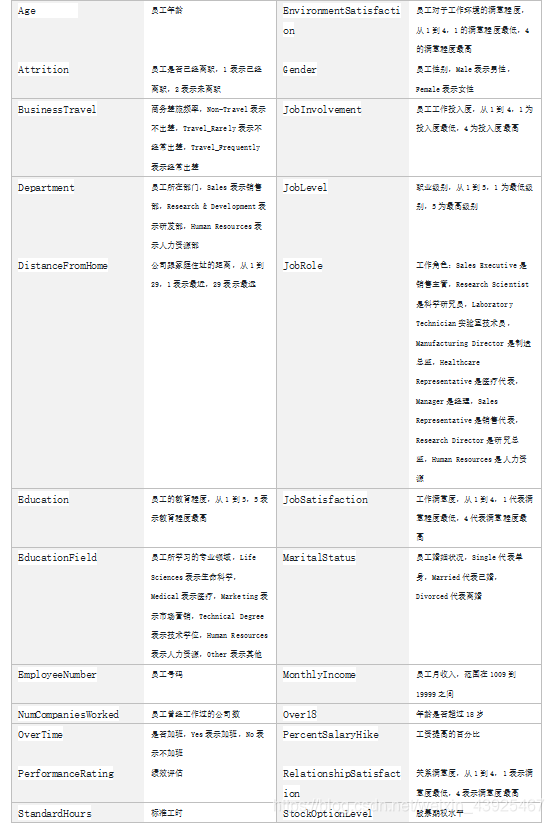
三. 步骤实现

1.导入并查看

首先进行观察使用的数据是csv文件格式，其中自变量30个，因变量为1个（是否离职）。数据集字符型字段有7个（BusinessTravel/Department/EducationField/Gender/JobRole/MaritalStatus/Over18/OverTime）数值型字段有24个。
导入需要的库

import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.model_selection import train_test_split,cross_val_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn import svm
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn import metrics 

导入数据

pd.set_option('display.max_columns',None)
pd.set_option('display.max_rows',None)
data_train = pd.read_csv('pfm_train.csv')
# 训练集总共1100条数据
data_test = pd.read_csv('pfm_test.csv')
# 测试集总共350条数据
data = pd.concat([data_train,data_test],axis = 0)

查看基本信息

data.head()
data.info()
data.describe()

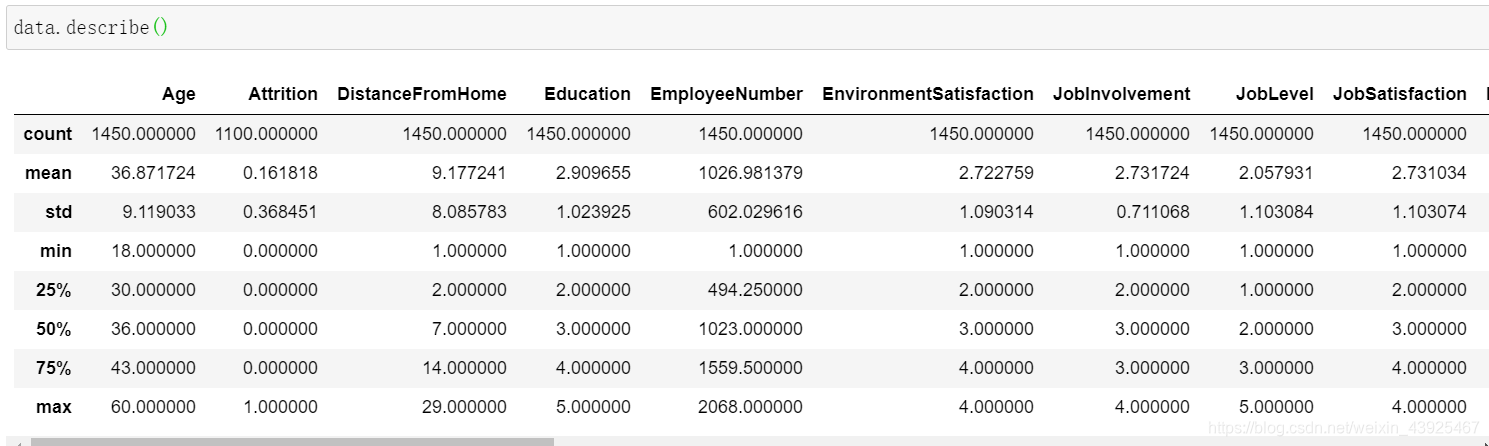
删除常量

data.drop('EmployeeNumber',axis=1)
data.drop('Over18',axis=1)
data.drop('StandardHours',axis=1)

2.数据探索性分析

#-*- coding: utf-8 -*-
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] 
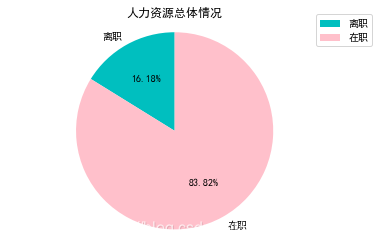
plt.title('人力资源总体情况')
labels = [u'离职',u'在职'] 
sizes = [data['Attrition'].value_counts()[1], data['Attrition'].value_counts()[0]] 
colors = ['c','pink'] 
patches,text1,text2 = plt.pie(sizes,labels=labels,colors=colors,autopct = '%3.2f%%', shadow = False, startangle =90, pctdistance = 0.6) 
plt.legend(loc="upper right",fontsize=10,bbox_to_anchor=(1.1,1.05),borderaxespad=0.3)
plt.axis('equal')
plt.show()
print('离职人员：',data['Attrition'].value_counts()[1])
print('在职人员：',data['Attrition'].value_counts()[0])
#离职人员178人，占比16.18%；在职人员922人，占比83.82%

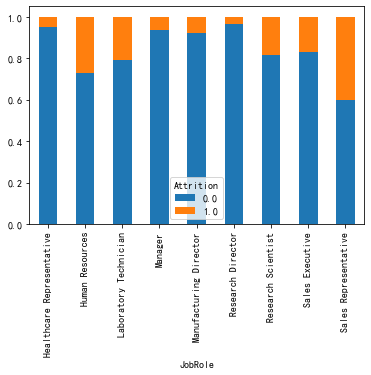
#各个职位中离职和未离职人数占比——柱状图

data_JobRole=pd.crosstab(data.JobRole,data.Attrition)
data_JobRole.div(data_JobRole.sum(1).astype(float), axis=0).plot(kind='bar', stacked=True)

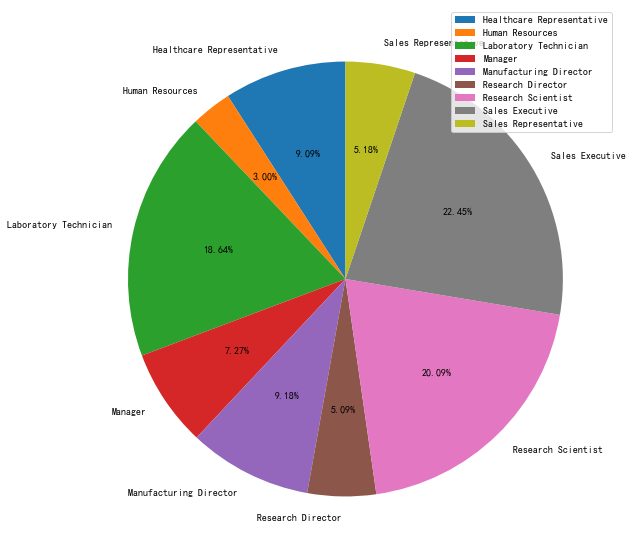
plt.figure(figsize=(10, 10))
data_Attrition_JobRole =data.groupby('JobRole').Attrition.count()
plt.pie(data_Attrition_JobRole, labels=data_Attrition_JobRole.index, autopct="%1.2f%%",startangle=90)
plt.legend()

3.数据处理

def resetAge(name):if (name < 24) & (name > 18) & (name == 58):return 1elif (name == 18) & (name == 48) & (name == 54) & (name == 57) & (name > 58) :return 0else:return 2def resetSalary(s):if s>0 & s<3725:return 0elif s>=3725 & s<11250:return 1else:return 2def resetPerHike(s):if s >= 22 & s < 25:return 0elif (s >= 11 & s < 14) | (s > 14 & s < 22):return 1else:return 2data['PercentSalaryHike'] = data['PercentSalaryHike'].apply(resetPerHike)
data['MonthlyIncome'] = data['MonthlyIncome'].apply(resetSalary)
data['Age'] = data['Age'].apply(resetAge)numerical_cols = data.select_dtypes(exclude = 'object').columns
categorical_cols = data.select_dtypes(include = 'object').columns
feature_cols=[col for col in numerical_cols if col not in ['EmployeeNumber','Over18','StandardHours']]
x_data=pd.concat([data[feature_cols],data[categorical_cols]],axis=1)
y_data=data['Attrition']
x_data=pd.get_dummies(x_data)

查看数据之间相关性

corr=x_data.corr()
corr

热力图进行表示

plt.figure(figsize=(16, 16))
sns.heatmap(corr,xticklabels=corr.columns.values,yticklabels=corr.columns.values)
plt.show()

也可以直接根据皮尔逊相关系数选择与要预测的属性列Attrition相关性最高的10个属性

features = data.corr()['Attrition'].abs().sort_values(ascending=False)[:11]
features.drop('Attrition', axis=0, inplace=True)
features = features.index
features

4.模型分析

进行编码并删除无用变量

cata_result = pd.DataFrame()
for i in data.columns:if data[i].dtype == 'O':cata = pd.DataFrame()cata = pd.get_dummies(data[i], prefix=i)cata_result = pd.concat([cata_result, cata], axis=1)for i in data.columns:if data[i].dtype == 'O':data = data.drop(i, axis=1)data = pd.concat([data, cata_result], axis=1)

代入模型

sep = 1100
X = data.iloc[0:sep,:].drop('Attrition',axis = 1)
y = data.iloc[0:sep,:]['Attrition']
data_test_use = data.iloc[sep:,:]
data_test_use1 = data_test_use.drop('Attrition',axis=1)X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.25,random_state=2)model = {'LR': LogisticRegression(), 'svm': svm.SVC(), 'RMF': RandomForestClassifier(random_state=10, warm_start=True,n_estimators=26,max_depth=6,max_features='sqrt'),'CART': DecisionTreeClassifier(), 'KNN': KNeighborsClassifier()}for i in model:model[i].fit(X,y)score = cross_val_score(model[i],X,y,cv=5,scoring='accuracy')print("%s:%.3f(%.3f)"%(i,score.mean(),score.std()))

逻辑回归效果最好

训练集准确度能达到90%，测试集能达到86.9%

5.结果分析

(1) 可视化的结果分析

从三个满意度进行分析

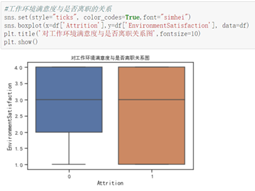
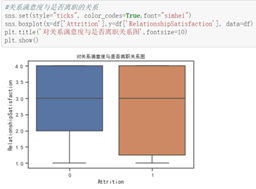
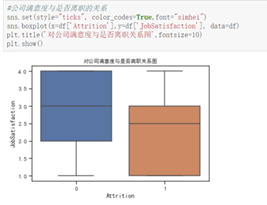
由图分析得，离职的员工对工作环境和关系的满意度出现了较低的评分，但中位数相当，故不作为决定性影响因素，而公司满意度出现了明显特征：离职员工的评分整体偏低，且离职人员对公司满意度整体波动较大。故公司满意度对员工离职的影响较大。

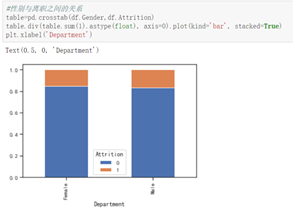
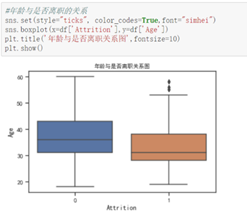
从性别上来看男性偏多。从年龄上看，离职的人比在职的人整体年龄偏低，并且 24之前和58岁的人员流动很大，而在年龄分段之内离职倾向不大，趋于缓和，部分的特数值没有离职人员。

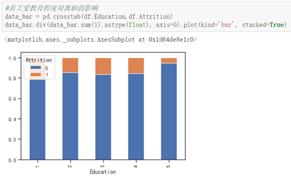
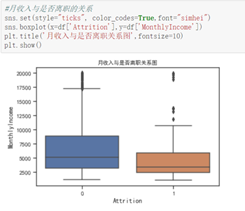
从受教育程度上来看，受教育程度最高的，离职率越低，受教育程度低的，离职率高，而受教育程度中等的差别不大。从月收入来看，表现出明显的月收入低的人，离职的波动越大。

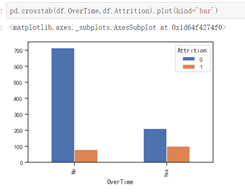
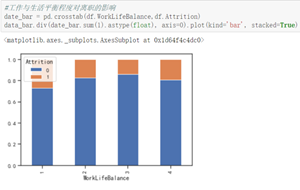
在职的人群中，不加班的占大多数，离职的人群中，加班所占比例较大。工作与生活平衡程度较低和较高的时候都容易出现离职现象

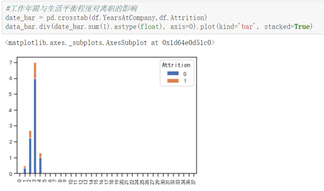
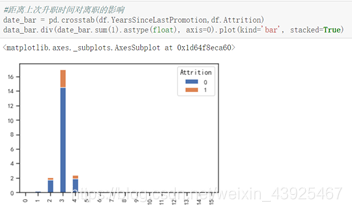
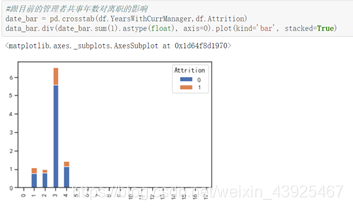
数据集中在0-4年，第2，3年离职的人数较多；距离上次升职时间为3年，跟目前管理之共事3年，出现离职现象较多。


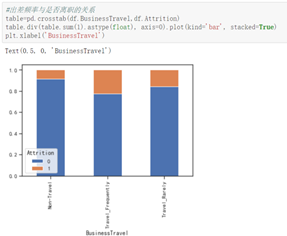
研发部门的人离职率低，出差频率中等偏高的人更容易离职。

总体来说，离职人员约占总人数的16%，离职员工的月收入比在职员工偏低，，大学专业和出差频率两项有明显的影响，经常出差的人流动性大。男性员工离职的更多，单身职员的离职的概率比较大，职业角色里，代理销售的人员流动大。可以刻画出形象，离职的人特征偏向单身男性代理销售，经常出差且月收入偏低，对公司满意度较低。

(2）特征选择结果分析

特征选择是从多维度的特征中选取出表征明显的特征显得非常的重要。特征选择主要可以从数据相关性角度和信息增益的角度来考虑。皮尔森相关系数也称皮尔森积矩相关系数，是一种线性相关系数，是最常用的一种相关系数。记为r，用来反映两个变量X和Y的线性相关程度，r值介于-1到1之间，绝对值越大表明相关性越强。通过计算，影响程度最高的分别为工作年限，年龄，职业级别，三个工作年限，月收入，股票期权，工作满意度和参与度。

(3)多模型交叉验证结果分析

预测并分类我们首先可以想到逻辑回归，根据输出，在不调参情况下，首选的逻辑回归具有较好的准确率。接着比较朴素贝叶斯和逻辑回归。由于逻辑回归和朴素贝叶斯分类器都采用了极大似然法进行参数估计，所以它们会被经常用来对比。.两者比较明显的不同之处在于，逻辑回归属于判别式模型，而朴素贝叶斯属于生成式模型。具体来说，两者的目标虽然都是最大化后验概率，但是逻辑回归是直接对后验概率P(Y|X)进行建模，而朴素贝叶斯是对联合概率P(X,Y)进行建模，所以说两者的出发点是不同的。朴素贝叶斯分类器要求“属性条件独立假设”即，对于已知类别的样本x，假设x的所有属性是相互独立的。这就导致了两点与逻辑回归的不同之处：朴素贝叶斯的限制条件比逻辑回归更加严格，意味着逻辑回归的应用范围更广。