线性代数

1. 从初等函数到高等数学

一元线性函数

在中学的初等数学里，把函数$f(x)=kx+b$ ($k,b$是不变量)，称为一元线性函数，因为在平面直角坐标系中这个函数的图形就是一条线，就是变量（包括自变量和因变量）之间的映射关系描述为一条线，把这种函数形象的称之为“线性”函数（如下图$L_1$）；如果$b=0$，则这个函数就变成了$f(x)=kx$的形式，也即是一条过原点的直线，如下图$L_2$。此时的变量之间的映射是单个数值之间的映射，这类单独的数我们称之为标量（scalar）。

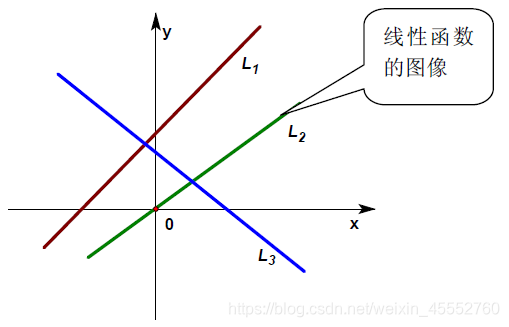
在大学的代数里，为了线性函数的进一步推广（如推广至双线性函数、多线性函数、线性空间、线性泛函，… …），把一元线性函数$f(x)=kx+b$的$b$舍掉，成了$f(x)=kx$的形式。即只有过原点的最简单的直线$f(x)=kx$才能被称为一元线性函数。因为只有这样才能满足线性函数性质。

线性函数性质：可加性和比例性

1）可加性：即如果函数$f(x)$是线性的，则有：和的函数等于函数的和。

$f(x_1+x_2)=f(x_1)+f(x_2)$

2)比例性：也叫做齐次性，数乘性或均匀性，即如果函数$f(x)$是线性的，那么有：比例的函数等于函数的比例；或者说自变量缩放，函数也同等比例地缩放。

$f(kx)=kf(x)$ 其中$k$是常数。

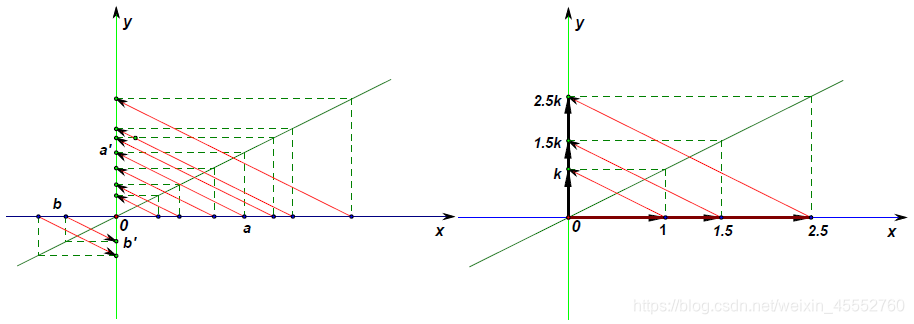
下图左右分别描述了最简单的标量映射($k>0$)及其基本性质:

2. 标量、向量、矩阵、张量

多元线性函数

事实上，高等数学里的线性概念正是从最简单的比例函数进行推广的，在大学里所学习的线性代数里的线性函数概念被推广成一个多元线性方程组所表示的映射关系。如方程组：

这与我们定义的$f(x)=kx$形式相去甚远，使形式统一，我们对变量进行了重新定义：

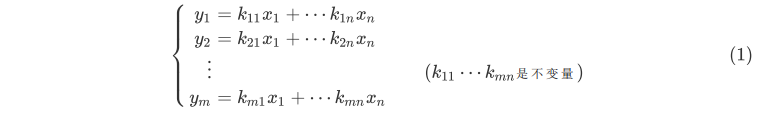
1）初等数学的线性函数的自变量由一个数$x$扩展为一个竖排的数组$\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$，应变量是一个数$y$也扩展

定义为一个竖排的数组$\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]$，这些$n$元数组和$m$元数组称之为列向量（vector）。

2）初等线性函数的比例系数$k$扩展为由所有$k_{ij}$构成的一个的数的方阵，称之为系数矩阵（matrix）：

$$\left[\begin{array}{cccc}{k}_{11}& k_{12}& \cdots & k_{1n}\\ k_{21}& k_{22}& \cdots & k_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ k_{m1}& k_{m2}& \cdots & k_{mn}\end{array}\right]$$

小结

标量、向量、矩阵、张量之间的联系

标量（scalar）
一个标量表示一个单独的数，它不同于线性代数中研究的其他大部分对象（通常是多个数的数组）。我们用斜体表示标量。标量通常被赋予小写的变量名称。

向量（vector）
一个向量表示一组有序排列的数。通过次序中的索引，我们可以确定每个单独的数。通常我们赋予向量粗体的小写变量名称，比如xx。向量中的元素可以通过带脚标的斜体表示。向量$X$的第一个元素是$X_1$，第二个元素是$X_2$，以此类推。我们也会注明存储在向量中的元素的类型（实数、虚数等）。

矩阵（matrix）
矩阵是具有相同特征和纬度的对象的集合，表现为一张二维数据表。其意义是一个对象表示为矩阵中的一行，一个特征表示为矩阵中的一列，每个特征都有数值型的取值。通常会赋予矩阵粗体的大写变量名称，比如$A$。

张量（tensor）
在某些情况下，我们会讨论坐标超过两维的数组。一般地，一个数组中的元素分布在若干维坐标的规则网格中，我们将其称之为张量。使用 $A$ 来表示张量“A”。张量$A$中坐标为$(i,j,k)$的元素记作$A_{(i,j,k)}$。

四者之间关系

标量是0阶张量，向量是一阶张量。举例：
标量就是知道棍子的长度，但是你不会知道棍子指向哪儿。
向量就是不但知道棍子的长度，还知道棍子指向前面还是后面。
张量就是不但知道棍子的长度，也知道棍子指向前面还是后面，还能知道这棍子又向上/下和左/右偏转了多少。

张量与矩阵的区别

• 从代数角度讲， 矩阵它是向量的推广。向量可以看成一维的“表格”（即分量按照顺序排成一排）， 矩阵是二维的“表格”（分量按照纵横位置排列）， 那么$n$阶张量就是所谓的$n$维的“表格”。 张量的严格定义是利用线性映射来描述。
• 从几何角度讲， 矩阵是一个真正的几何量，也就是说，它是一个不随参照系的坐标变换而变化的东西。向量也具有这种特性。
• 张量可以用3×3矩阵形式来表达。
• 表示标量的数和表示向量的三维数组也可分别看作1×1，1×3的矩阵。

3）然后定义一种系数矩阵与向量(矩阵)相乘的运算法则，则式(1)可以改写成如下形式：

$$\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]=\left[\begin{array}{cccc}{k}_{11}& k_{12}& \cdots & k_{1n}\\ k_{21}& k_{22}& \cdots & k_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ k_{m1}& k_{m2}& \cdots & k_{mn}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]\text{\hspace{1em}(2)}$$

式(2)与(1)等价。

矩阵和向量相乘结果

若使用爱因斯坦求和约定（Einstein summation convention），矩阵$A$, $B$相乘得到矩阵$C$可以用下式表示：
$$a_{ik}\ast b_{kj}=c_{ij}$$
其中，$a_{ik}$, $b_{kj}$, $c_{ij}$分别表示矩阵$A,B,C$的元素，$k$出现两次，是一个哑变量（Dummy Variables）表示对该参数进行遍历求和。
而矩阵和向量相乘可以看成是矩阵相乘的一个特殊情况，例如：矩阵$B$是一个$n\times 1$的矩阵。

4）式(2)可进一步简写为：

$y=f(X)=KX$

其中：$$y=f(X)=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right],K=\left[\begin{array}{cccc}{k}_{11}& k_{12}& \cdots & k_{1n}\\ k_{21}& k_{22}& \cdots & k_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ k_{m1}& k_{m2}& \cdots & k_{mn}\end{array}\right],X=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]。$$

到此为止，我们终于看到初等线性函数和高等线性函数的概念在形式上得到了统一，同时也引入了标量、向量、矩阵、张量等概念，这些在机器学习的计算中都是最常用的基本单元。那么，这些基本单元究竟应用于机器学习的什么地方呢？下面插入一个例子

例子：卷积是怎么回事？

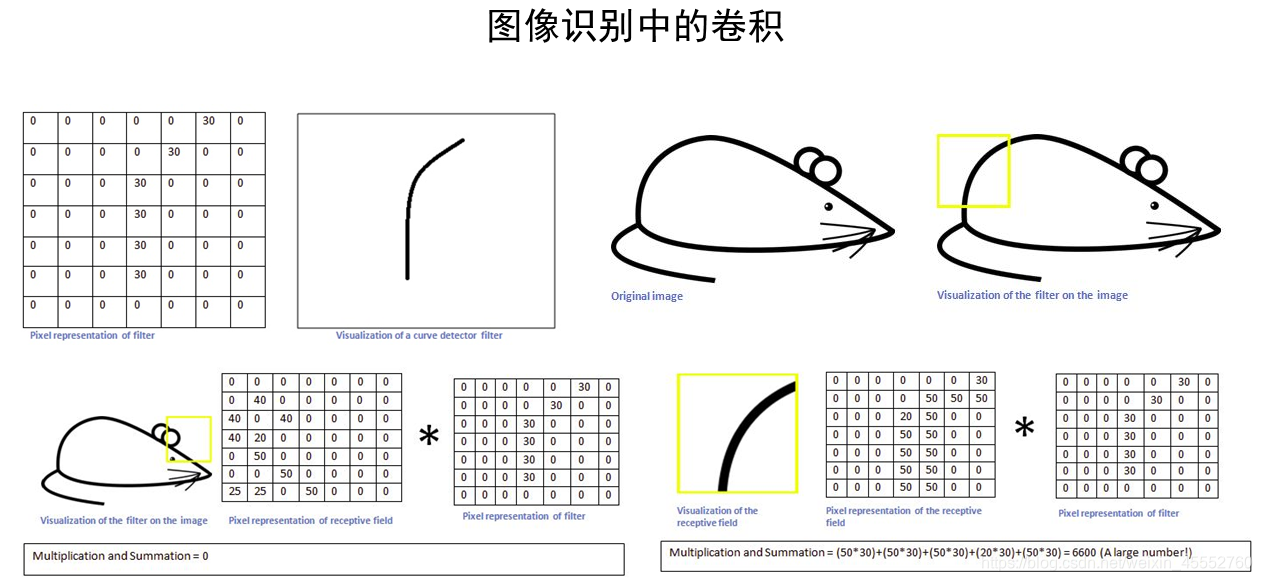
在最初接触图像处理的时候，我们一般是从图像的平滑（高低通滤波等）开始的，如下图所示：

• 如上图的平滑，一个典型的8领域平滑，其结果中的每个值都来源于原对应位置和其周边8个元素与一个$3X3$矩阵的乘积，也就相当于对原矩阵，按照顺序将各区域元素与$W$矩阵相乘， W W