大意:
n个顾客,每个人有一个购买的欲望bi,m件物品,每一件物品有一个价值ci,每一个顾客会买商品当且仅当bi+ci>=定价.
现在要求对每一个商品定价,求出它的最大销售值(数量*定价)
n,m<=2e5
思路:
首先m件物品都是相互独立的,可以看成m个询问
另外,不妨对n个人的购买力做一个降序排序,显然它们满足单调性
不难发现,一旦我们定下了物品的价格,那么最终的销售额就由销售数量决定,也就是会有多少人买。此时在销售数量减少的情况下,我们一定会尽可能地抬高价格。从而我们得到一个结论:每一个商品i的定价一定是bj+ci(1<=j<=n).这是因为,它刚好可以使某个人会买这件商品。假设最优定价不满足这个结论,显然我们可以直接抬高它使其达到另一个bj+ci,此时我们在购买人数不变的情况下就提高了单价,这是更优的。
现在商品单价就只有n个选择了,对于商品i,我们的销售额就是max{j*(bj+ci)}(1<=j<=n),因为我们是按购买力降序排序,如果第j个人刚好买的起,那么前面的人一定都买的起(这里也不用关心购买力重复的问题,因为重复的话,后面相同购买力的的人对应的决策一定会更好)。
此时我们就转化了题意:对于一个i(1<=i<=m),找到max{j*(bj+ci)}
继续
如果放到坐标系下来看的话(遇到双变量时,放到坐标系下往往是个不错的选择),我们令横坐标为ci(选择i也是可以的,因为i跟ci是一一对应的,但是考虑到我们是在对不同的价值做取舍,取ci会更加方便一点),纵坐标为对应的价值 , 也就是 j*(bj+ci),不同j的选择对应不同的总价值。
我们将ci表示成x,那么原本要求的值 max{j*(bj+ci)}(1<=j<=n) 转化为max{j*(bj+x)}=max{jx+j*bj},可以发现里面是一条直线的表达式。显然我们最后是要找一个这些直线在每一个横坐标下对应的最大值,也就是转化成了一个凸包。最后的答案就是横坐标对应的凸包上的点的纵坐标了
这里借一下官方题解的图片:
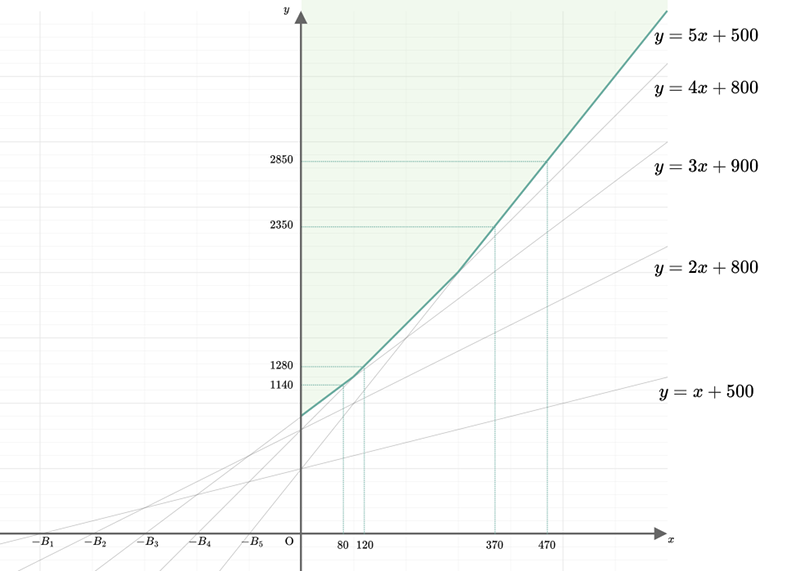
求凸包的话,我们从1-n开始遍历的话,直线的斜率是单调递增的,
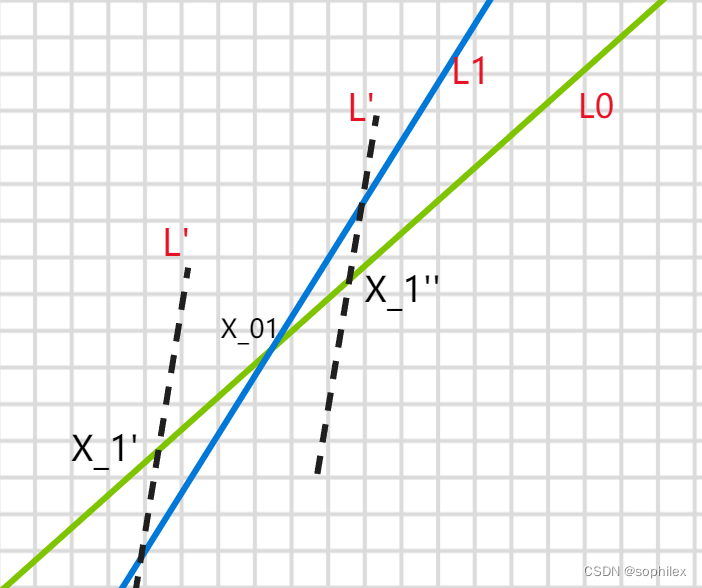
不妨用单调栈来更新当前段的最大值对应的直线
假设当前栈内有两条直线L0,L1,交点为X_01,那么对于新加入的直线L',如果它与L0的交点X_1'的横坐标小于X_01的横坐标,显然就可以把L1淘汰掉了,因为它后面也不会有比L‘更大的机会了。
关于这个判断,就只要计算一下交点横坐标就可以了。
最后我们得到了一个凸包,那么对于一个ci,我们去二分找到它在那一段线段上就可以了
时间复杂度O(n+mlogn)
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
#define mk make_pair
const ll N=2e5+10;
ll n,m;
ll b[N];
ll c[N];
struct P
{double x,y;
};
vector<pair<double,P>> vt;
double cross(P p1,P p2,P p3) {return (p2.x-p1.x)*(p3.y-p1.y)-(p3.x-p1.x)*(p2.y-p1.y);
}
bool judge(ll x,ll tar)
{return vt[x].first<=tar;
}
void solve()
{cin>>n>>m;for(int i=1;i<=n;++i) cin>>b[i];sort(b+1,b+1+n,greater<ll>());for(int i=1;i<=m;++i) cin>>c[i];for(int i=1;i<=n;++i){P p={(double)i,(double)i*b[i]};//y=ix+i*b[i]//上文说过直线可以用jx+j*b[j],所以我们就直接用两个参数来表示对应的直线,可以说p就代表一条直线while(vt.size()>=2&&cross(p,vt.rbegin()->second,(next(vt.rbegin()))->second)<0) vt.pop_back();
//cross函数是在计算新加入的直线是否要把里面这一条直线弹出,也就是在计算交点横坐标是否满足条件。这个可以自己推一下//弹出无用的直线double x=0;if(vt.size()){P pp=vt.back().second;x=(pp.y-p.y)/(p.x-pp.x);} vt.push_back(make_pair(x,p));} ll len=vt.size();
// for(auto i:vt)
// {
// cout<<i.second.x<<" "<<i.second.y<<endl;
// }for(int i=1;i<=m;++i){ll l=0,r=len-1;while(l<=r){ll mid=l+r>>1;if(judge(mid,c[i])) l=mid+1;else r=mid-1;}P op=vt[l-1].second;cout<<(ll)(op.x*c[i]+op.y)<<" ";}
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
// ll t;cin>>t;while(t--)solve();return 0;
}