背景:本人在整理资料时翻找出来的以前做的研究自己写的总结,2017年发布在《Maritime Policy & Management》期刊的一篇关于国际班轮航运合作博弈的英文文献,本人本着学习的目的就文献的重点内容进行了浅层次的解读,就自己的理解整理了如下知识点。请感兴趣的研究人员去查看原文献,以下公布的内容仅供研究类似合作博弈问题的人员参考。

(2017)国际班轮航运的合作博弈
摘要:在海运中,承运人在竞争的同时又彼此合作以求优化各自的利润。在这样的环境下,合作博弈在承运人间建立了。本文构建了一个非线性混合整数问题以求确定单家航运公司最优的合作水平,以及将得到的最优结果嵌入常规的博弈理论框架。运用包含上升方向搜索技术的对角化算法有效的求解该博弈问题。数值试验的结果表明承运人一般会选择相同的合作水平去实现自身利润的最大化,在一般情形下合作博弈能够实现均衡。
3.合作模型
模型的基本假设:(1)航运市场中存在好几家航运公司彼此间既竞争又合作;(假设合作博弈的基本情形是客观存在的)
(2)承运人都有各自的航线去满足OD对间的顾客运输需求,航线上的运价或是运输成本会受到市场需求变动的影响;
(3)市场上的运输需求包括原始需求和引人需求。原始需求是合作发生之前就已经存在的需求,引人需求是合作行为发生后产生的额外需求。引人需求可能来自将运输任务交由其他联盟的承运人运输的顾客;
(4)航线的运价或成本是市场需求的函数,市场需求是合作水平的函数;
(5)假设承运人间是平等竞争的,不存在领导者和跟随者的关系;
(6)假设承运人间的服务是可以相互取代的;
(7)假设该博弈问题是两阶段的连续静态博弈,并且是完全信息博弈,即合作的双方都是知道对方所采取的行动的;(第一阶段:承运人合作去减少平均成本和增加总的市场利润;第二阶段:承运人选择竞争水平去增加自身的利润)
(8)为引人需求构造虚拟的运输路径;
(9)承运人彼此竞争的目的除了获得原始需求的利润,还是为了得到在博弈的第一阶段产生的引人需求的利润;




3.1. 单个承运人利润最大化的模型
该模型是一个混合整数非线性模型。
公式(1):承运人的利润计算公式。承运人通过为运输任务选择运输路径获得利润。集装箱转运在实际航运操作中是一种典型的现象,该模型可以表示集装箱转运的情况,通过选择集装箱运输路径来表现承运人将集装箱转运的情况。但是集装箱的转运仅仅影响成本或利润而不会影响模型均衡结果的取得(强调本文也考虑了集装箱转运操作)。承运人只能按照他在市场上的竞争水平获得引入需求的部分利润。
公式(2):容量约束。某一条弧可能是承运人b多条航线都经过的,弧上的集装箱可能是来自同一个承运人的不同运输任务,给弧设置一个不同承运人可以通过的最大流量上限(可以看成是承运人在该弧上的最大运力)。
公式(3):每个承运人的运输任务都能被完成。通过为每一个运输任务安排唯一的一条运输路径,确定所有被选路径上的运输任务运量等于该承运人需要完成运输的集装箱总量。
公式(4):保证每一个运输任务都只有唯一的一条运输路径。确保同一个运输任务不能被分批进行运输。
公式(5):根据承运人的合作水平,确定该承运人可以得到的吸引集装箱运量。将在集合B中的承运人看作是一个联盟,联盟成员的总合作水平决定可以吸引的集装箱量,再根据成员各自愿意付出的合作水平(可以看成是承运人付出了的合作成本)来分配总的集装箱吸引量。如果合作水平y使用金钱来衡量,那么(本文只考虑20英尺的集装箱)表示承运人b为引入一个集装箱需要付出多少钱,表示承运人投入1美元可以得到多少个引入的集装箱数量。(是一个给定的固定值,不会随市场合作情况的变化而变化)承运人的合作水平和竞争水平具体可以看作是承运人可以在联盟中获得的集装箱吸引量。
公式(6):当吸引的集装箱量是正数时才存在虚拟路径。
公式(12):函数1。假设承运人b需要付出的合作成本是承运人b合作水平的函数。
公式(13):函数2。承运人b在路径r上的单位运价是市场总运输需求的函数。
公式(14):函数3。承运人b引入的集装箱量的运价是市场总运输需求的函数。
公式(15):函数4。承运人b在路径r上的单位运输成本是市场总运输需求的函数。
公式(16):函数5。承运人b引入的集装箱量的单位运输成本是市场总运输需求的函数。
3.2. 合作博弈的理论框架
上文提出的只是使一个承运人利润最大化的模型,在市场中承运人应该考虑其他承运人的合作和竞争水平来实现自身利润的最大化,研究市场上所有承运人的利润最大化问题可以在合作博弈的理论框架下进行。
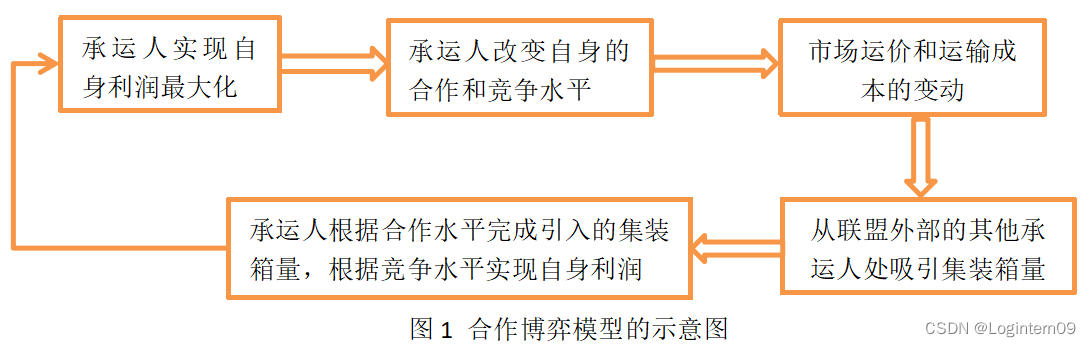
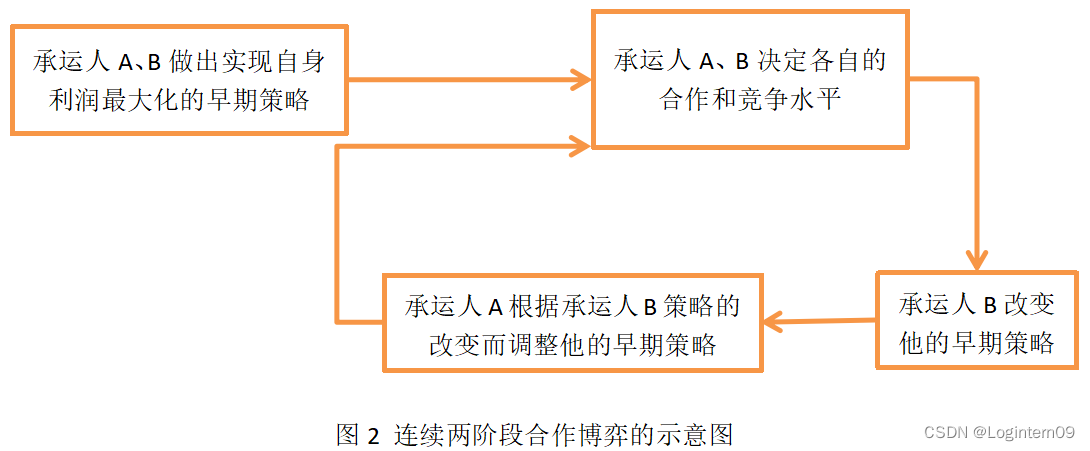
这一过程持续到没有任何承运人可以通过改变他的早期策略来使其受益。
4.求解方法
提出基于上升的优化方法去求解单个承运人的利润最大化问题,然后运用对角化算法求解多个承运人的合作博弈问题。早期研究表明对角化算法能有效求解这一类型的博弈问题(说明为什么运用对角化的方法求解该合作博弈问题,理论支持)。假设其他承运人的早期策略不变,改变某一个承运人的早期策略使其在目前阶段他的利润最大化,将该承运人变动后的合作和竞争水平作为外生的数据提供给第二个需要改变策略的承运人。通过不断迭代,最终达到任何承运人都不愿意再改变自身早期策略为止,将该结果看作是使合作博弈达到稳定的最优结果。
4.1. 运用基于上升优化的方法求解单个承运人的利润最大化问题
由于公式(1)-(16)提出的模型是混合整数非线性模型,常规的求解器不能有效的求解该模型。因此,本文提出一个基于上升优化的方法求解该模型。
将单个承运人利润最大化的问题分解为两个子问题:(1)确定合作水平的问题;(2)路径选择的问题。分别求解这两个子问题,其中一个子问题的结果影响另外一个子问题的结果。不断迭代求解这两个子问题直到满足收敛准则。
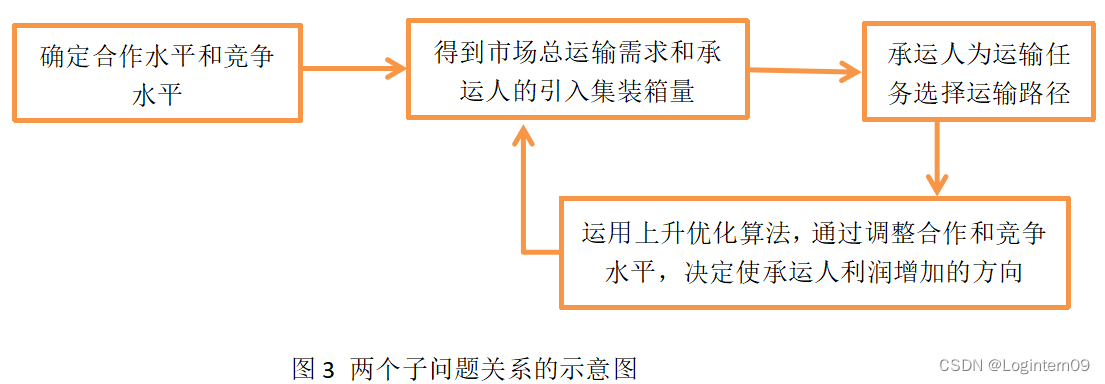
基于上升优化方法的步骤如下:
(1)初始化
确定迭代次数n,承运人b需要支付的合作成本,竞争成本,原始集装箱运输需求,承运人b的运输任务集装箱运量,判断某一条弧是否在运输任务可行的路径上,合作水平,竞争水平。在初始阶段,本文假定承运人b不与任何承运人合作或竞争。
(2)路径选择
该问题可以运用求解最短路的算法进行计算,当承运人b的运输需求是较大的,并且超过了弧上的最大容量,该问题就变成了求解最小成本的网络流问题(由模型的约束条件(3)可知运输任务都是需要被完成的,所以在收益一定的情况下,为了使利润最大化只有使成本最小),也是可以运用相应的算法在多项式时间内有效求解的。
(3)找出一个可行的上升方向
通过改变承运人b的合作和竞争水平,找出一个改善的方向。分别对合作水平和竞争水平求利润的偏导数,合作水平的偏导数说明合作水平变动对利润的影响,如果该偏导数的值是正数说明增加合作水平会增加承运人的利润。
如果在一定的迭代次数内路径选择的结果不变,将步长变为,继续迭代过程。
(4)收敛性测试
如果两次连续的迭代间的合作水平和竞争水平小于给定的某个极小值,得出最佳的结果和停止迭代,否则返回第(2)步。
4.2. 合作博弈的对角化算法(雅克比算法)
(1)初始化
确定迭代次数n,合作成本,竞争成本,总的市场需求量。初始化承运人b的合作水平,竞争水平。
(2)对角化
使用第n-1次迭代的信息,运用基于上升优化的方法求解承运人b的最大利润。
(3)收敛性测试
如果两次连续的迭代间的合作水平和竞争水平小于给定的某个极小值,得出最佳的结果和停止迭代,否则返回第(2)步。
5.数值实验
随机生成实验数据,使用C语言进行编程实现算法。在第一个数值实验中,假设合作网络中存在两个承运人,他们之间共享网络,彼此可以使用对方的船舶。
给定原始的运输网络,在弧上注明弧的容量,初始成本和初始运价。承运人间的合作可以产生吸引需求,吸引需求用虚拟的路径表示。
给出每一条可行集装箱运输路径的成本函数和运价函数(合作对成本的影响比运价的影响大)。该函数表明引入需求的增加减少了路径上的成本和运价。
(1)确定承运人的航线集合(给出某几条航线)
(2)随机产生可以利用上述航线进行运输的集装箱运输任务
(3)给出合作水平成本函数,引入需求的运价,引入需求的成本。
5.1. 上升优化方法的有效性
通过与Lingo软件求解的结果对比测试该方法的有效性。通过小规模实验的比较,发现使用上升优化优化算法得到的结果与使用精确解软件Lingo得到的结果差距很小(Lingo的结果优于优化算法求解的结果),在问题规模较大时,认为使用上升优化算法得到的解接近最优解。
5.2. 两个承运人的合作博弈
假设两个承运人有相同的航运网络,并且初始运输需求相同。
(1)第一次迭代:承运人a确定合作策略,计算在合作水平和竞争水平下的利润;承运人b在初始阶段的合作水平和竞争水平为0,完成初始的运输任务获得利润。(在初始阶段,承运人a可以设置较高的合作水平和较低的竞争水平,因为此时承运人b不会对承运人a的策略做出反应)
(2)第二次迭代:承运人b选择合作策略,承运人a与承运人b共享利润,承运人a的利润下降。(由于承运人b的决策在承运人a之后做出,所以在前面的迭代阶段承运人b获得的利润要低于承运人a)
(3)承运人b投入更多的钱用于合作吸引外部需求和投资增加自身的竞争能力,承运人b的利润会逐渐增加,最终达到与承运人a相同的利润水平。
(4)在第一次迭代,市场中只有承运人a拥有合作和竞争能力,此时可以将该市场看作是寡头垄断市场,在第二次迭代,承运人b积极参与市场活动,但是此时市场已经足够大了(承运人a吸引了足够大的运输需求,承运人b参与市场是从承运人a处瓜分市场需求),所以在第二次迭代阶段市场规模是减小的。
(5)当承运人a察觉了承运人b的竞争行为,他开始减少在合作方面的投资,此时市场规模会急剧的下降。
5.3. 竞争成本的灵敏度分析
竞争成本变动10%-200%,(竞争成本:为了达到竞争水平而需要承运人支付的金额)观察到竞争水平是下降的,但合作水平几乎不发生变化,得出“竞争成本的变动不会影响合作水平”的结论。实现情况下,当承运人的竞争水平提高时,承运人更愿意合作扩大其市场规模,使合作的成员都受益。但本文中承运人的利润计算公式主要受到竞争水平的影响,所以当承运人的竞争成本增加,竞争水平会相应的下降,对合作水平的影响不明显。
5.4. 合作成本的灵敏度分析
合作成本变动10%-100%,(合作成本:为了达到合作水平而需要承运人支付的金额)观察到合作水平和竞争水平都呈下降趋势,得出“合作成本的增加会使承运人的合作和竞争水平下降”的结论。由于合作行为会影响航线的成本和运价,因此合作成本的变动会直接影响承运人的合作和竞争水平。参与人通过彼此间的合作扩大市场规模,承运人的市场需求会增加,增加的市场需求将影响该承运人的合作和竞争水平。
5.5. 合作对市场规模(市场需求)的灵敏度分析
在实际的航运市场中,价格的变动对集装箱运输需求的变动影响作用不大。换句话说,成本和运价的变动不会引起额外的市场需求。因此,本文研究合作对市场规模的影响,由于合作直接影响运价和成本,所以通过合作对市场规模做灵敏度分析,可以看出价格对市场需求的影响程度。
得出“如果合作水平是足够高的,市场规模是急剧增加的”这一结论。市场规模的增加是比某一特定承运人合作水平的增加要大的。
5.6. 合作对航线成本、运价和市场规模的影响
生成四种情景,研究在不同情景下合作行为对航线成本、运价和市场规模的影响。
情景(1):航线成本和运价较低,承运人不愿意支付额外的合作成本,不选择合作的策略,选择竞争策略更有利于承运人获取较高的利润;
情景(2):承运人合作后会产生成本的节约,但是需要付出的合作成本是高于这个成本节约的,所以承运人不愿意选择合作的策略;
情景(3):航线成本较低,市场需求较多时,承运人更愿意合作;(市场规模较大时,承运人更倾向于合作而不是竞争)
情景(4):航线成本较低,航线运价较低,市场需求较多时,承运人的合作和竞争意识会更弱;
5.7. 三个承运人的合作博弈
三个承运人有相同的航线网路和运输需求。对角化算法的步骤调整如下:承运人a做出合作水平的策略,将结果告知承运人b,承运人b做出决策告知承运人a和承运人c,在承运人a和承运人b做出决策后,承运人c根据已知的信息做出使其利润最大化的决策。重复这一过程直到没有承运人可以通过调整合作水平使其利润增加。
结论:(1)先进入市场的承运人具有优势,主要是开拓市场,后做出决策的承运人只能在前一个承运人策略的基础上调整自己的策略使获得较高的利润。迭代后期,三个承运人的竞争能力都达到了相近的水平,市场趋于稳定。
(2)三个承运人合作博弈的市场规模比两个承运人博弈得到的市场规模要大。
(3)在市场内引入新的参与者,增加了原先的市场内参与者的竞争水平。
(4)三个承运人的合作博弈,个体的合作水平下降了,但是市场整体的合作水平上升了。
5.8. 承运人的数量对均衡结果的影响
结论:
(1)随着承运人数量的增加,市场规模和总利润增加。
(2)随着承运人数量的增加,市场规模和总利润增加的比率下降。原因是当承运人的数量增多和市场利润稳定时,合作后改善的服务无法再吸引更多的运输需求。
(3)合作水平增加比率比竞争水平增加比率低,说明承运人彼此间的竞争更明显。原因是当合作水平提高,市场规模趋于稳定时,承运人不愿意投入更多的资金合作扩大市场,此时承运人的目标更多的是竞争市场份额,使自身的利润最大化。
6.结论
数值实验的结果表明承运人会选择相同的合作水平去谋求自身利润最大化,合作博弈在一般情况下能达到均衡。
当前的研究可以在如下几个方面进行优化:(1)在不对称信息条件下研究承运人间的合作博弈,博弈的均衡点可能会发生变化;
(2)研究不确定市场需求条件下的合作博弈问题;
(3)本文使用的数据是假设性的数据,能够使用航运公司真实的数据用于研究合作博弈问题是更具有意义的;
(4)对角化算法的收敛性证明是重要的;
(5)承运人利润的构成可能包含其他的因素,例如承运人的累积努力,新的承运人的加入,战略联盟的协议等。