【Linux网络编程】传输层协议

一，传输层的介绍

二，UDP协议

2-1，UDP的特点

2-2，UDP协议端格式

三，TCP协议

3-1，TCP报文格式

3-2，TCP三次握手

3-3，TCP四次挥手

3-4，滑动窗口

3-5，流量控制

3-6，紧急指针

四，TCP/UDP对比

一，传输层的介绍

传输层负责数据能够从发送端传输接收端，毫无疑问，这里需要传输层需要拿到IP地址和对应程序的端口号。IP地址就是网络中主机的地址；端口号就是应用程序的地址，它标识了一个主机上进行通信的不同的应用程序。

当网络中的不同主机进行通信时，具体流程如下图：

端口号范围划分

0 - 1023：知名端口号。这些端口号是分配给系统级别的服务和应用，如HTTP服务运行在80端口，HTTPS运行在443端口，SSH服务运行在22端口等，这些服务协议的端口号都是固定的。
1024 - 65535：操作系统动态分配的端口号。这些端口号是客户端程序的端口号，是由操作系统从这个范围动态分配的。

对于知名端口号，存储在系统文件 /etc/services 中，我们可以使用指令：cat /etc/services 查看。当我们自己写一个程序使用端口号时，一定要避开这些知名端口号。

netstat工具和pidof工具

netstat是一个用来查看网络状态的重要工具指令。

语法：netstat [选项]
功能：查看网络状态
常用选项：
-n：拒绝显示别名，能显示数字的全部转化成数字。
-l：仅列出有在 Listen(监听) 的服務状态。
-p：显示建立相关链接的程序名。
-t（tcp简写）：仅显示tcp相关选项。
-u（udp简写）：仅显示udp相关选项。
-a（all简写）：显示所有选项内容。

pidof用于查找正在运行进程的ID（PID）。它在查看服务器的进程id时非常方便。

语法：pidof [进程名]
功能：通过进程名，查看进程id

二，UDP协议

2-1，UDP的特点

UDP是面向数据包的，即应用层交给UDP多长的报文，UDP直接一次性发送，它不做任何处理。UDP没有真正意义上的发送缓冲区，它是直接将数据交给内核, 由内核将数据传给网络层协议。UDP具有接收缓冲区，但是这个接收缓冲区不能保证收到数据的顺序和发送数据的顺序一致，要是缓冲区满了，再到达的UDP数据就会被丢弃。

2-2，UDP协议端格式

UDP（用户数据报协议）协议报头格式相对简单，每个UDP报文分为UDP报头和UDP数据两部分，报头在数据的前面，具体格式的说明如下：

UDP报头由4个16位长（2字节）的字段组成，总共8个字节。这些字段分别说明该报文的源端口、目的端口、报文长度和校验值。结构如下图：

源端口：

占用16位，用于标识发送端的端口号。在表示不需要接收端回复数据的情况下，源端口号可以不指定，此时其值为0。

目的端口：

占用16位，用于标识接收端的端口号。

UDP长度：

占用16位，表示UDP数据包的总大小，包括报头和数据部分。这里长度字段的单位是字节，也就是说一个UDP能传输的数据最大长度是：2^16 - 1 = 65535字节，即64KB(包含UDP报头)。若需要传输的数据过大，就需要我们自己在应用层手动的分包，多次发送，并在接收端手动拼装。

校验值：

占用16位，用于错误检查，如果接收端在校验时发现了错误，将会立即丢弃该数据报。

三，TCP协议

TCP要保证数据的可靠性传输，同时又要提高性能，所以底层结构会相当的复杂。还有，TCP虽然能保证数据的可靠传输，但还会出现丢包情况。下面来具体研究TCP协议。

3-1，TCP报文格式

TCP（传输控制协议）是一种面向连接的、可靠的、基于字节流的传输层通信协议，它是对数据的传输进行一个详细的控制。TCP报文分为报头和数据两部分，具体的格式如下：

源/目的端口号：

表示数据是从哪个进程来，到哪个进程去。

32位序号：

TCP是一种可靠的传输协议，它使用的是序号与确认序号来保证数据的可靠传输。

序号是一个32位的字段，用于标识发送端发送字节流中每一个字节的顺序编号。在连接建立时，初始序号（ISN）是随机生成的。接收端使用这个序号字段来重组数据包，确保数据按正确顺序接收。例如，发送端的ISN为1000，那么第一个数据段的序号字段值为1000，第二个数据段的序号字段值为1000加上第一个数据段的长度，依此类推。序号确保了TCP传输的有序性。

序号在TCP通信的整个过程中都起着重要作用。在TCP建立连接（三次握手）时，序号用于标识发送数据的起始位置；在数据传输过程中，序号用于确保数据的顺序传输；在连接关闭时，序号也参与确保数据传输的完整性。

32位确认序号：

确认序号也是一个32位的字段，序号用于发送端标识数据，而确认序号用于接收端确认接收的数据。在TCP通信过程中，每当接收端成功接收到一个报文段后，就会向发送端发送一个包含确认序号的确认报文段，以告诉发送端数据以成功接收，保证了数据传输的可靠性，过程具体如下。

TCP保证数据传输的可靠性是以发送与应答实现的。收到应答表示数据以收到，确认序号就是用于告诉发送端，接收端已经成功接收了哪些数据，以及接收下一个什么序号的数据，若发送方在规定的时间内没有接收到应答，那么发送方就判定接收方没有收到数据（数据也可能是阻塞在路由中或其它情况），发送方就可能进行重传报文。注意：确认序号与序号通常同时存在，即接收方在应答的同时也顺便发送数据，即捎带应答。

确认序号的数值就是接收字段最后一个字节的序号值加一，即表明了该序号之前的所有数据已经正确无误地收到，也指明了下一个期待收到的字节序号。例如，接收端收到序号为1000到1999的数据段后，发送的确认报文中确认序号字段的值应为2000，表示已成功接收到1000到1999字节，且期望下一个字节为2000。

最后要说明一下，这种应答功能是由操作系统自动完成，确认序号只有当标志位ACK标志为1时才有效。

4位TCP报头长度：

报头长度是以4字节为基本单位的，表示该TCP头部有多少个32位bit（即有多少个4字节）。TCP头部最大长度是 (2^4 - 1) * 4 = 60字节。

6位标志位：

标志位用于控制数据传输中的特定行为，哪个标志位置为1，就对应哪个标志位的特定功能。以下是这6位标志位的详细介绍：

        URG：紧急指针是否有效，标识紧急指针，下面会具体说明。
        ACK：确认号是否有效。该标志表示应答域有效。当进行应答时，该标志位会置为1。
       PSH：提示接收端应用程序立刻从TCP缓冲区把数据读走，将缓冲区中的数据尽快向上方交付。
RST：表示对方要求重新建立连接。TCP建立通信连接时可能会出故障，该标志表示重新开始建立TCP连接。我们把携带RST标识的称为复位报文段。 SYN：表示本报文要请求建立连接。当SYN标志置位时，表示发送端希望初始化一个连接。该标志在TCP建立连接中运用。我们把携带SYN标识的报文称为同步报文段。
        FIN：该标志用于结束一个TCP连接。当FIN标志置位时，表示发送端已经发送完所有数据，并请求关闭连接。我们称携带FIN标识的为结束报文段。

16位窗口大小：

表示发送该TCP报文的接受窗口还可以接受多少字节的数据量。这个字段用于流量控制，告知发送端，接受端的缓存大小，以此控制发送端发送数据的速率。下面会详细说明。

16位校验和：

用于确保传输的数据的完整性。它用一种简单的计算方法来确保数据的可靠传输。该位置发送端进行填充，接收端进行校验。如果校验不通过，则认为数据有问题。此处的校验和包含TCP首部和TCP数据部。

16位紧急指针：

标识数据中哪部分数据是紧急数据。当运用紧急指针时，URG标志位置为1，操作系统会优先读取该报文数据。

选项：

长度不定，最大40字节，暂时先忽略。

数据部分：

TCP报文段中的数据部分是可选的。在一个连接建立和一个连接终止时，双方交换的报文段仅有TCP首部。下面所说的报文段，都是指没有数据部分的报文。

3-2，TCP三次握手

TCP通信需要先建立起连接，如TCP套接字。TCP连接是通过三次握手来建立的。

第一次握手：客户端向服务器发送一个SYN报文段。这个报文段中的SYN标志位被置为1，表示客户端希望与服务端建立连接，同时指定自己的初始序号为x。此时，客户端从CLOSED状态进入SYN_SENT状态，即从关闭状态进入请求连接状态，等待服务器的确认。

第二次握手：服务器收到客户端的SYN报文段后，知道客户端请求建立连接。于是，服务器将SYN和ACK（SYN用于向客户端发起请求建立，ACK用于确认收到客户端的SYN报文段）标志位都置为1，确认序号字段的值设置为x+1（表示对客户端初始序号的确认），并随机产生一个自己的初始序号y，然后将这个SYN+ACK报文段发送给客户端，以确认连接请求。此时，服务器从LISTEN状态（监听状态，表示该端口是开放的，在等待被连接）进入SYN_RCVD状态（收到和发送一个连接请求后等待对方对连接请求的确认状态）。

第三次握手：客户端收到服务器的SYN+ACK报文段后，客户端将标志位ACK置为1，确认序号字段的值设置为y+1（表示对服务器初始序列号的确认），并将这个ACK报文段发送给服务器。服务器成功收到后，连接成功建立，服务器从SYN_RCVD状态进入ESTABLISHED状态（连接成功状态），随后就可以开始传输数据。

最后说明下，TCP三次握手属于建立连接的过程，是由双方操作系统自动完成。最开始阶段，双方连接都是处于CLOSED连接关闭阶段，在TCP套接字中，当服务端调用listen函数使服务器处于监听状态时，服务端TCP层就从CLOSED状态变为LISTEN状态。客户端使用connect向服务端请求建立连接，即一次挥手，客户端TCP层就从CLOSED状态变为SYN_SENT状态，connect阻塞等待服务器应答；这时，服务端一旦监听到连接请求，listen函数返回，服务端TCP层从LISTEN状态变为SYN_RCVD状态，并将该连接放入内核等待队列中。这里服务端还会向客户端发送ACK确认报文和SYN请求建立连接报文，即二次挥手；客户端收到报文段（之所以叫报文段是因为这里的报文是没有数据部分的）后，会向服务端发起ACK报文段以确认连接建立请求，connect函数返回，客户端TCP层从SYN_SENT状态变为ESTABLISHED状态，即三次握手；当服务端收到确认报文段后，连接成功建立，服务器从SYN_RCVD状态进入ESTABLISHED状态，accept函数返回，通信开始。至于中间功能，都是依靠操作系统来完成。

注意：第一次握手和第二次握手都是有应答的（捎带应答），第三次握手客户端向服务端发送数据时并没有应答，这里客户端默认的是服务端成功接收建立连接，若这里的第三次握手没有成功发送到服务端，客户端就开始向服务端发送数据了，这时，服务器端就会给客户端进行应答——发送RST报文段，告诉客户端要重新进行三次握手建立连接，即连接重置。还有，TCP连接是双方共同发送一次连接请求和确认一次连接请求，理论上，这至少需要四次握手来确认，但在实际应用中，第二次和第三次握手的过程可以合并，即捎带应答，因此最终只需要三次握手。

建立连接为什么要三次握手？

如果采用一次握手，在网络状况不佳的情况下，这个连接请求没有及时到达服务器，客户端可能会连续多次发送连接请求报文，而服务器却无法区分当前收到的请求是新的还是之前因网络堵塞而过期的请求。这可能导致服务器错误地接受或拒绝连接请求。除此外，服务器中还可能存在多个客户端发送的连接，即闲置连接（连接建立好但不用），使其维护成本过大，浪费资源。还有，一次握手过于简单，没有服务器的确认步骤，很容易使服务器受到其它主机的“连接”攻击。

如果采用两次握手，那么当第二次握手服务器向客户端发送一个SYN+ACK（确认）包作为响应时，由于服务器没有收到响应，这里服务器就会默认客户端收到数据，成功建立连接，若第二次握手客户端没有收到服务端发送过来的确认报文，客户端会重新开始请求建立连接，又会使服务器存在多个闲置连接。

三次握手是建立一个可靠双向数据传输通道的最小值。首先要明白，连接的建立是通信双方共同完成的，双方都要有一次发送数据以请求建立连接和收到应答以确认连接建立，只不过三次握手这里使用的是捎带应答。三次握手可以说是通信双方连接建立的最小成本，若握手次数过多，这里不仅会导致连接建立时间过长，还会导致连接建立过于复杂，维护连接的成本过大，浪费资源。其次，三次握手还可以解决网络中延迟的重复分组问题。例如，如果客户端发送的SYN报文段，由于网络延迟而迟迟未到达服务器，客户端可能会重发SYN报文段；如果此时原始的SYN报文段到达服务器，服务器会发送ACK报文段进行确认，但客户端在收到这个ACK报文段时，由于认为自己并未请求连接（因为它已经重发了SYN报文段并收到了新的确认），所以会忽略该ACK报文段，这样，就不会因为网络延迟而导致错误的连接建立。

TCP通信过程

当三次握手建立好连接时就可以开始双方的通信了。在TCP通信过程中，数据发送可能出现丢失或阻塞在路由及应答阻塞或丢失多种情况，发送方无法确定具体情况，这里采取的策略是若在一个特定的时间内（时间由网络状况而定，因为数据阻塞与网络状况有关）发送方没有收到应答，它就会重新发送，这种行为叫做超时重传。若报文重复收到（数据阻塞在路由中的情况，并没有丢失），发送方根据序号的唯一性会进行去重；若数据重传累计到一定的次数，TCP就认为网络或对方主机出现异常，强制关闭连接。

3-3，TCP四次挥手

TCP通信完毕后断开连接需要四次挥手，用于确保通信双方都能正常结束数据传输。四次挥手与三次握手基本相似——满足双方共同的需求，即请求关闭连接和确认对方连接关闭的请求，只是因为三次握手使用捎带应答，而四次挥手是具体分步进行，具体细节如下：

第一次挥手：客户端向服务器发送一个FIN报文段（FIN标志位被置为1），表示客户端没有数据要发送给服务器了，请求关闭连接，即TCP套接字客户端开始调用close函数。此时，客户端进入FIN_WAIT_1状态，其报文段序号等于前面已经传送过来数据的最后一个字节的序号加1。

第二次挥手：服务器收到客户端的FIN报文段后，发出一个ACK报文段（ACK标志位被置为1）进行确认，表示确认客户端没有数据要发送了。此时，服务器进入CLOSE_WAIT状态。注意：此时服务器可能还有数据需要发送给客户端，所以服务器还不会立即关闭连接通道。

第三次挥手：服务器向客户端发送一个FIN报文段，表示服务器也准备好关闭连接，即TCP套接字服务端调用close函数。此时，服务器进入LAST_ACK状态，等待客户端的确认。

第四次挥手：客户端收到服务器的FIN报文段后，发送一个ACK报文段进行确认。此时，客户端进入TIME_WAIT状态，服务器收到客户端的ACK报文段后，关闭连接并进入CLOSED状态。客户端在等待一段时间后，如果没有收到服务器的重传FIN报文段，则认为连接已经正常关闭，也可以关闭连接并进入CLOSED状态，即TCP套接字中close函数成功调用释放资源返回。

TCP套接字中，当我们启动服务端、客户端时，若强行终止服务端程序，如：按下Ctrl-C键，这时我们在以绑定相同的IP地址和端口号运行服务端后，会出现 bind error：Address already in use 错误提示，这是因为虽然服务端程序终止了，但TCP协议层的连接并没有完全断开，即四次挥手没有全部完成，IP地址和端口号资源还在被占用，因此不能再次监听同样的IP地址和端口，我们可以用netstat命令进行查看。

最后说明一下，四次挥手的发起者并非固定为客户端，服务器也可以首先发起第一次挥手。TCP协议规定，主动关闭连接的一方是处于TIME_ WAIT状态，若我们使用Ctrl-C先终止了服务端，那么服务端就是主动关闭连接的一方，而挥手流程基本一致。

断开连接为什么要四次挥手？

TCP连接是可靠传输且全双工连接，即数据可以在两个方向上同时传输。因此，当一方想要关闭连接时，需要分别关闭两个方向上的数据传输通道并要告知对方本地连接要关闭（确认对方关闭通道的请求），这就是为什么需要四次挥手的原因：第一次和第二次挥手关闭客户端到服务器的数据传输通道，第三次和第四次挥手关闭服务器到客户端的数据传输通道。还有，TCP四次挥手是一个复杂但必要的过程，它确保了TCP连接的可靠终止和资源的正确释放。

TIME_WAIT状态

在客户端处于TIME_WAIT状态下，客户端会等待一段时间（注意，这段时间足以保证两个方向上的数据都被丢弃，使得原来连接的数据包在网络中都自然消失），因为这里已经是最后一次挥手，没有确认报文段（报文段不知道是否成功被对方接收），客户端不知道服务端是否成功收到ACK确认报文段关闭连接通道。这里有两种情况：1，服务端成功接收到确认报文。2，ACK报文段丢失，服务端向客户端重传FIN报文段，客户端这里仍处于TIME_WAIT状态。

注意：客户端在TIME_WAIT状态结束后，延迟的FIN报文段到达的情况根本不会存在。TIME_WAIT状态持续的一段时间通常是2MSL，即最大报文生存时间。MSL是TCP报文段在网络中能够存活的最长时间，超过这个时间，报文段将被丢弃。2MSL的时间足以保证在两个传输方向上的尚未被接收或迟到的报文段在网络中都已经消失。MSL具体的数值可通过 cat /proc/sys/net/ipv4/tcp_fin_timeout 查看，查看如下。

TIME_WAIT状态的目的

TIME_WAIT状态不仅可以确保客户端发送的最后一个ACK报文段能够到达服务器，还能够处理由于网络延迟而导致重发的ACK报文段。当进行到四次挥手客户端向服务端发送ACK确认报文段时，如果这个ACK报文段丢失了，服务器在超时后会重新发送FIN报文段。客户端在TIME_WAIT状态下会进行等待一段时间，确保收到这个重传的FIN报文段并作出响应。如果收到了之前连接的延迟报文段，这些报文段将被丢弃。

为什么TIME_WAIT状态等待的时间是2MSL?

首先，TCP具有重传机制，这里重点看第三次挥手和第四次挥手，当发送方（发送FIN报文断）未收到接收方的确认（ACK）时，会重传未确认的报文段。注意：ACK报文段发出时，发送方就已经处于TIME_WAIT状态，若报文丢失，最坏情况是经过了MSL时间，重传的FIN报文段在最坏情况下也需要经过MSL时间（由于网络延迟），因此，IME_WAIT状态等待2MSL是能够保证重传报文段一定被接收。

其次，断开连接后，网络中还可能存在之前的延迟报文，若没有等待足够的时间让这些报文从网络中消失，那么当尝试建立新的连接时，这些迟到的报文可能会被错误地当作新连接的数据进行处理，导致数据错乱，而MSL是TCP报文的最大生存时间，只有一方主机是能够处于TIME_WAIT状态，因此TIME_WAIT持续存在2MSL的话就能保证在两个传输方向上的尚未被接收或迟到的报文段都已经消失。

3-4，滑动窗口

上面我们讨论了确认应答策略，对每一个发送的数据段，都要给一个ACK确认应答，收到ACK后再发送下一个数据段。这样做有一个比较大的缺点，就是性能较差，尤其是当网络状况不佳的情况下。

一发一收的方式性能较低，那么我们一次发送多条数据，就可以大大的提高性能（其实是将多个段的等待时间重叠在一起了）。TCP滑动窗口机制允许发送方在不需要等待每个数据段的确认应答的情况下连续发送多个数据段，并确保数据的有序传输，防止发送方发送数据过快导致接收方处理不过来。

下面来说明一下窗口大小。窗口大小指的是无需等待确认应答而可以继续发送数据的最大字节。上图的窗口大小就是4000个字节(四个段)，发送前四个段的时候，不需要等待任何ACK，可以直接发送。

发送方的滑动窗口

滑动窗口位于缓冲区。在发送方，滑动窗口用于控制可以连续发送但尚未得到接收方确认的数据量。发送方的窗口大小取决于接收方通过TCP头部中的 “窗口大小” 字段通知的最大可接受数据量和网络情况（网络状况会影响数据的传输速率）。这个窗口会在发送方的缓冲区中移动，表示当前允许发送的数据范围。

窗口左边界：指向最早未被确认的数据字节。
窗口右边界：指向允许发送的最大序列号，即当前窗口的末尾。

当接收方确认数据后，窗口会向右滑动，允许发送更多数据。发送方的缓冲区这里可以分为三部分：滑动窗口左边的部分是已经发送并得到应答的数据，滑动窗口中的数据是可发送的部分，滑动窗口右边的数据是待发送的部分。滑动窗口向右滑动就是准备发送右边的数据。

接收方的滑动窗口

在接收方，滑动窗口用于管理接收缓冲区中的数据。接收窗口的大小取决于接收缓冲区中剩余的空间量和接收方处理数据的能力。接收方通过TCP头部的“窗口大小”字段向发送方报告其接收窗口的大小，从而控制发送方的发送速率。

接收窗口左边界：指向下一个期望接收的字节序号。
接收窗口右边界：指向接收缓冲区能够容纳的最大字节序号，即当前窗口的末尾。

当接收方成功处理并应用数据后，它会通过发送ACK（确认）报文来更新窗口大小，以便发送方发送数据。

滑动窗口的大小

滑动窗口的大小是可变的，它会根据影响因素变大变小。滑动窗口的本质其实是缓冲区中一段的空间，它通过起始的下标和结束的下标来表示窗口的大小。滑动窗口不会向左移动，窗口变大时，起始下标向右移动的速度比结束下标移动的速度满；窗口变小时，起始下标向右移动的速度比结束下标移动的速度快；窗口向右移动就是两个下标向右移动。

TCP报文格式中，窗口大小只有16位，16位数字最大表示65535，那么滑动窗口最大就是65535字节么？实际上，TCP首部选项字段中还包含了一个窗口扩大因子M，实际窗口大小是窗口字段的值左移 M 位。这里了解即可。

滑动窗口中的丢包问题

丢包问题分为发送包丢失和应答包丢失。

发送包丢失

TCP通信中，丢包问题是靠应答机制解决的，即确认序号。但要注意，确认序号表示该序号之前的所有数据被完整接收，倘若有一个比丢失报文对应的确认序号大确认号返回，那么就等于告诉发送端，该丢失的报文被完整接收，这显然是错误的。因此，这里是按丢包之前的确认序号返回的，如下图：

如上图，当某一段报文段丢失之后，发送端会一直收到 1001 这样的ACK报文段，就像是在提醒发送端 “我想要的是1001” 一样。如果发送端主机连续三次收到了同样一个 “1001” 这样的应答，就会将对应的数据 1001 - 2000 重新发送，这种机制被称为高速重发控制(也叫快重传)。这个时候接收端收到了 1001 之后，再次返回的ACK就是7001了，因为 2001 - 7000 接收端其实之前就已经收到了，它被放到了接收端操作系统内核的接收缓冲区中。还有就是操作系统内核为了维护这个滑动窗口，会开辟发送缓冲区来记录当前还有哪些数据没有应答，只有确认应答过的数据，才能从缓冲区删掉。

这里有个问题，若窗口大小不足以连续发送三次的确认报文呢？这种情况就会进行超时重传。

应答包丢失

应答包丢失其实根本不影响。若前面或中间的数据应答包丢失了，后面的确认序号就能表示应答功能，因为，确认序号表示该序号之前的数据都已被接收；若是最后一个数据的应答包丢失，发送方会进行超时重传。

3-5，流量控制

接收端处理数据的速度是有限的。如果发送端发的太快，导致接收端的缓冲区被打满，这个时候如果发送端继续发送，就会造成丢包，继而引起丢包重传等等一系列连锁反应，因此TCP支持根据接收端的处理能力，来决定发送端的发送速度，这个机制就叫做流量控制。

TCP利用滑动窗口机制来实现流量控制。滑动窗口机制中，发送方发送的数据量受到接收方窗口大小的限制，如果接收方处理数据的速度较慢，导致接收窗口变小，接收方会在确认应答中告知发送方新的窗口大小。发送方收到后，就会相应地减少发送的数据量，以适应接收方的处理能力；如果接收方处理速度较快，接收窗口变大，接收方也会通知发送方。此时，发送方可以增加发送的数据量，提高数据传输效率。

滑动窗口机制中，接收端将自己可以接收数据缓冲区的大小放入TCP首部中的 “窗口大小” 字段中，通过ACK报文通知发送端。其中，窗口大小字段越大，说明网络的吞吐量越高，接收方接收能力越强，若接收端一旦发现自己的缓冲区快满了，就会将窗口大小设置成一个更小的值通知给发送端。发送端接受到这个窗口之后，就会减慢自己的发送速度。如果接收端缓冲区满了，就会将窗口置为0，这时，发送方不再发送数据，但发送方会定期发送一个窗口探测数据段（因为窗口大小可能为0，所以报文里没有数据部分），使接收端把窗口大小告诉发送端。接收方也会主动将窗口更新的通知发送到发送方，即双方都会主动，这样的好处是可以尽快恢复正常通信。

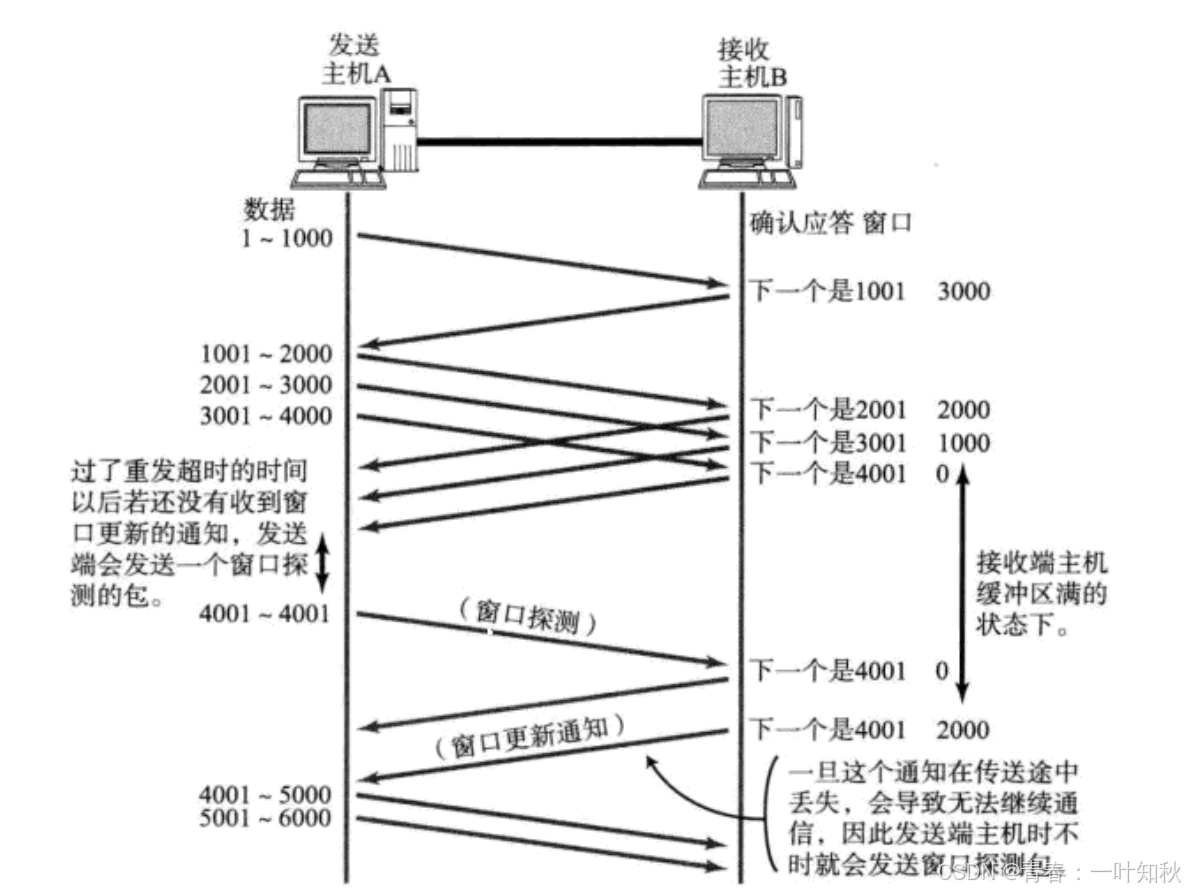
若接收方主机的窗口大小一直为0不做处理呢？这时发送方会发送PSH标志位，用于提示接收端立即将缓冲区中的数据，将其递交给应用程序的应用层代码，而不是在缓冲区的队列中排队等待。注意：PSH只是在操作系统方面上进行调整，若应用层代码没有处理，这里就是程序员本身写的代码问题。

3-6，紧急指针

TCP报文中的紧急指针是一个特殊且重要的字段。紧急指针存在于TCP头部的选项字段中，是一个16位的正偏移量。它指向紧急数据在整个数据流中的位置。紧急指针的主要作用是在TCP连接中提供紧急数据的传输机制，当发送端需要发送一些紧急数据时，可以设置紧急指针来指示接收端，在接收到该指针之后尽快处理这些数据。

TCP头部中有一个URG标志位，用于表示紧急指针是否有效。当URG=1时，表示紧急指针有效；当URG=0时，则忽略紧急指针值，也就是说只有当URG标志置1时，接收端才会根据紧急指针的值来处理紧急数据。

最后说明下，紧急指针实际中基本不会用到，这里了解即可。