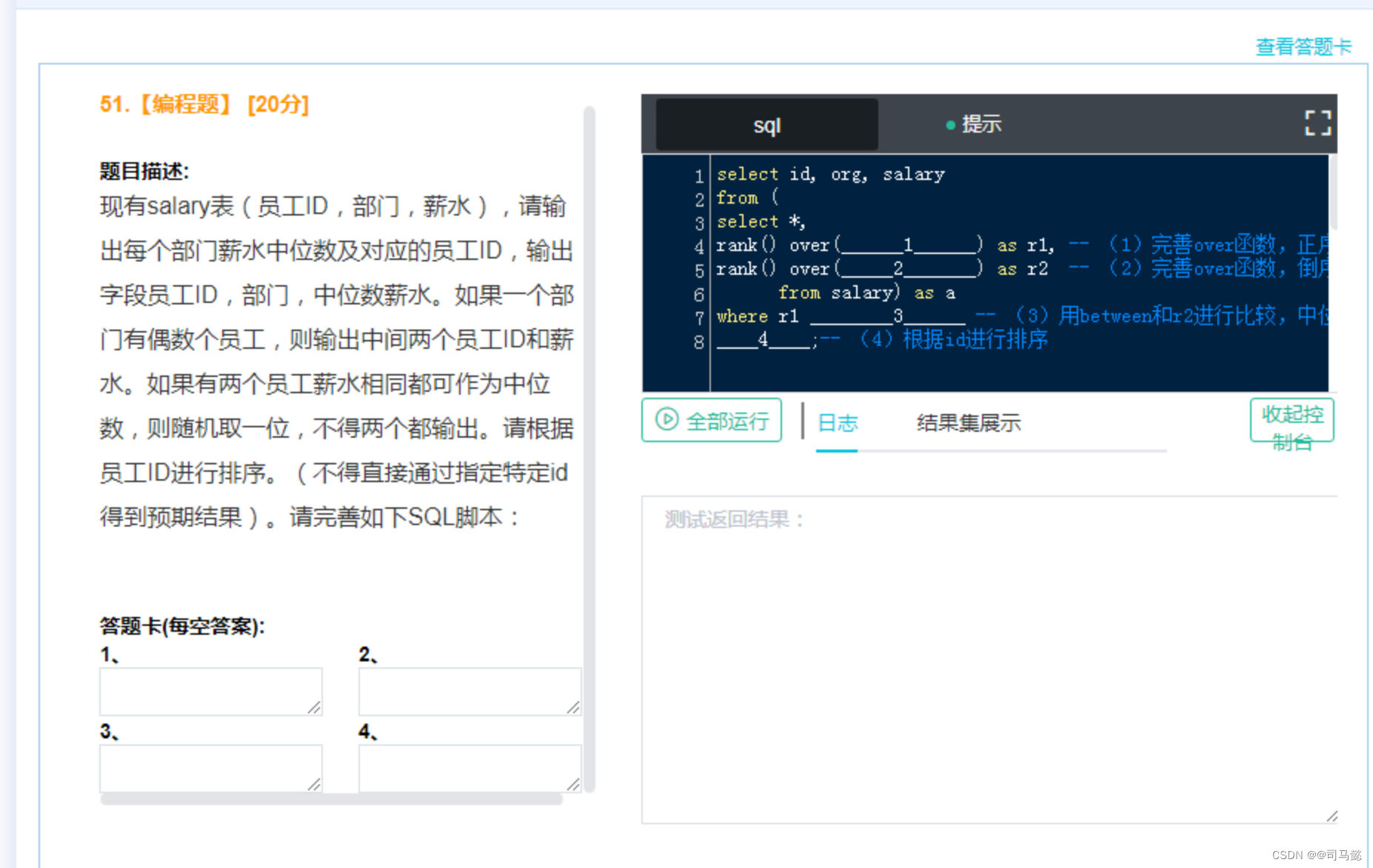
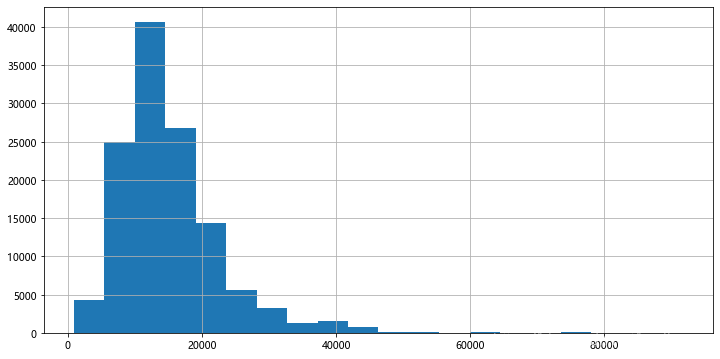
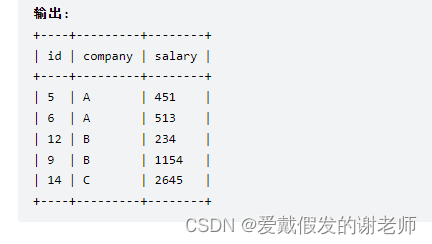
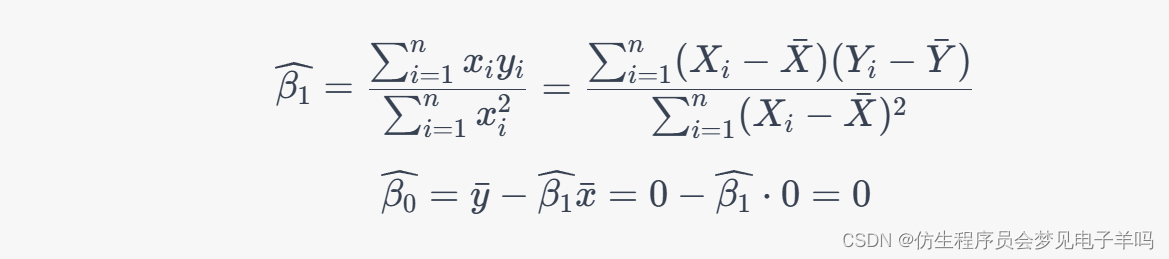第二次作业:
教材:伍德里奇。计量经济学导论:现代观点(第五版)。
第三章习题:必做 1,2,5,6,11,选做13
第四章习题:必做2,3,4,5,8,选做9,10,11
第三章
1.多元线性回归模型的基本假设是什么?在证明最小二乘估计量的无偏性和有效性的过程中,哪些基本假设起了作用?
多元线性回归模型的基本假设: 在多元线性回归模型中,我们通常假设以下条件成立: 线性关系:自变量和因变量之间存在线性关系;
多元正态性:误差项 ϵ \epsilon ϵ 服从均值为零、方差为常数 σ 2 \sigma^2 σ2 的多元正态分布;
没有多重共线性:自变量之间不存在高度相关的情况; 同方差性:误差项 ϵ \epsilon ϵ 的方差在不同自变量的取值范围内保持恒定;
独立性:误差项 ϵ \epsilon ϵ 是独立的,即不受其他误差项的影响。
在证明最小二乘估计量的无偏性和有效性的过程中,主要起作用的假设是多元正态性和同方差性。其中,多元正态性假设使得最小二乘估计量服从正态分布,从而能够进行假设检验和置信区间估计;同方差性假设则使得最小二乘估计量具有最小方差的性质,从而具有较好的精确性和可靠性。此外,若多重共线性存在,则最小二乘估计量可能会偏离真实值,失去无偏性和有效性。因此,多重共线性的检验和处理也是建立可靠多元线性回归模型的重要步骤。
2.在多元线性回归分析中,t检验与F检验有何不同?在一元线性回归分析中,二者是否有等价的作用?

t检验与F检验在多元线性回归分析中的不同:
t检验通常用于检验单个自变量对因变量的显著性,它计算了该自变量系数与标准误的比值,从而判断该系数是否显著不为零;
F检验通常用于检验所有自变量对因变量的联合显著性,它计算了回归平方和与残差平方和的比值,从而判断所有自变量的联合效应是否显著不为零。
在一元线性回归分析中,t检验与F检验有等价的作用:
当只有一个自变量时,t检验与F检验的结果是等价的。此时,t检验可以用于检验单个自变量对因变量的显著性,F检验可以用于检验回归模型的整体显著性,这两种方法得到的结果应该是一致的;
具体而言,当只有一个自变量时,F检验的计算公式等价于对该自变量的t检验的平方,即 F = t 2 F = t^2 F=t2。
总之,t检验和F检验在多元线性回归分析中有不同的作用,但在一元线性回归分析中,它们有等价的作用。
5.考虑下列两个模型:
- Y i = α 0 + α 1 X i 1 + α 2 X i 2 + u i Y_i=\alpha_0+\alpha_1 X_{i1}+\alpha_2 X_{i2}+u_i Yi=α0+α1Xi1+α2Xi2+ui
- Y i − X i 1 = β 0 + β 1 X i 1 + β 2 X i 2 + v i Y_i-X_{i1}=\beta_0+\beta_1 X_{i1}+\beta_2 X_{i2}+v_i Yi−Xi1=β0+β1Xi1+β2Xi2+vi
(1)证明: β 1 ^ = α ^ 1 − 1 , β 0 ^ = α ^ 0 , β 2 ^ = α ^ 2 \widehat{\beta_1}=\widehat{\alpha}_1-1,\widehat{\beta_0}=\widehat{\alpha}_0,\widehat{\beta_2}=\widehat{\alpha}_2 β1 =α 1−1,β0 =α 0,β2 =α 2.
(2)证明:两个模型的最小二乘残差相等,即对任何 i i i,有 u i ^ = v ^ i \widehat{u_i}=\widehat{v}_i ui =v i
(3)在什么条件下,模型2的 R 2 R^2 R2小于模型1的 R 2 R^2 R2?
(1) 首先,将模型2转化为标准形式: Y i = β 0 + β 1 X i 1 + β 2 X i 2 + ( v i + X i 1 ) Y_i=\beta_0+\beta_1 X_{i1}+\beta_2 X_{i2}+(v_i+X_{i1}) Yi=β0+β1Xi1+β2Xi2+(vi+Xi1)。
然后,将模型1和模型2的误差平方和分别表示为:
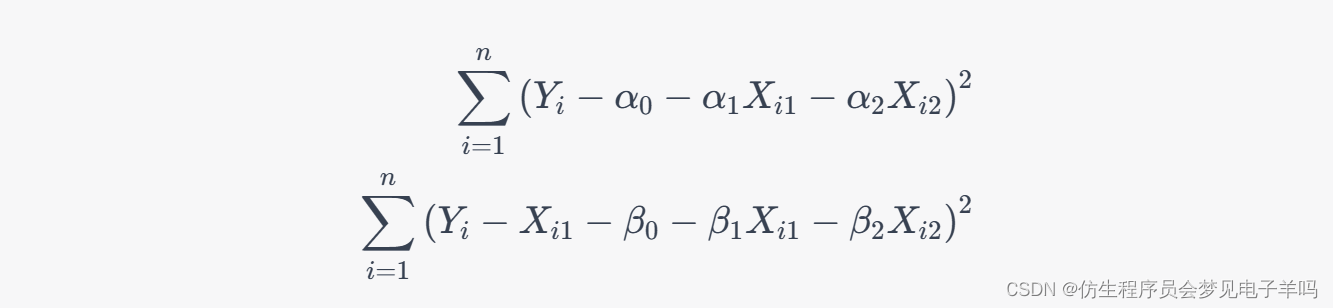
为了证明 β 1 ^ = α ^ 1 − 1 , β 0 ^ = α ^ 0 , β 2 ^ = α ^ 2 \widehat{\beta_1}=\widehat{\alpha}_1-1,\widehat{\beta_0}=\widehat{\alpha}_0,\widehat{\beta_2}=\widehat{\alpha}_2 β1 =α 1−1,β0 =α 0,β2 =α 2,我们只需要将模型2的误差平方和中的第二个括号展开,然后将模型1和模型2的误差平方和分别代入,得到:
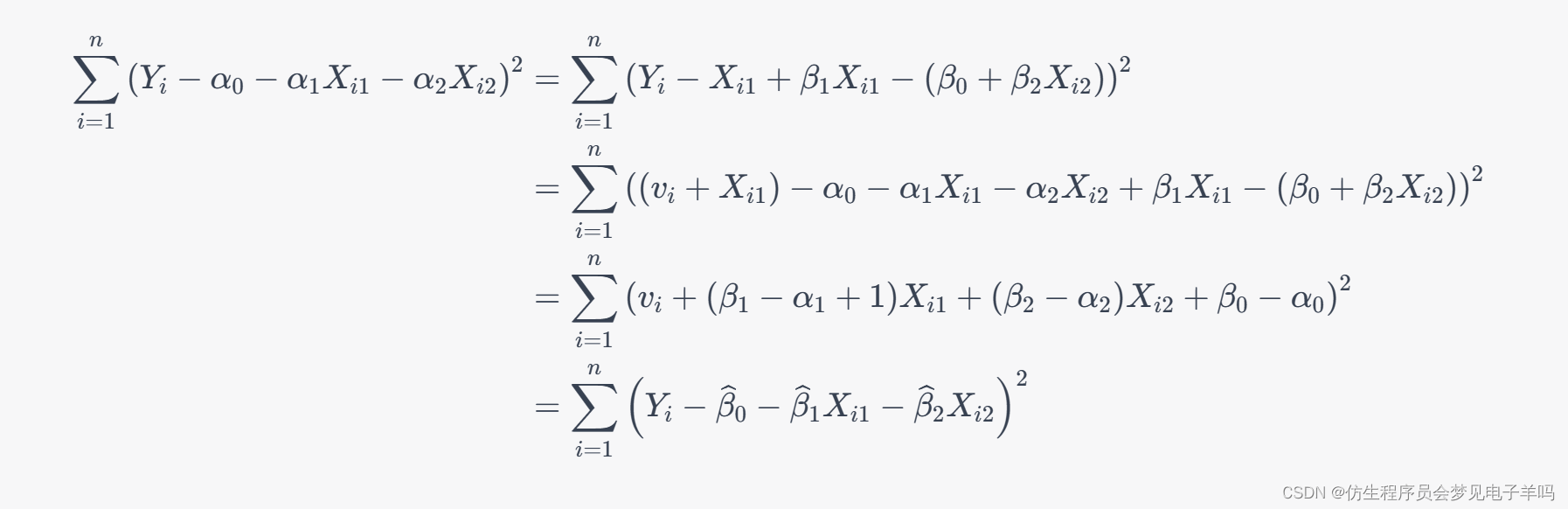
因此,我们可以得到 β 1 ^ = α ^ 1 − 1 , β 0 ^ = α ^ 0 , β 2 ^ = α ^ 2 \widehat{\beta_1}=\widehat{\alpha}_1-1,\widehat{\beta_0}=\widehat{\alpha}_0,\widehat{\beta_2}=\widehat{\alpha}_2 β1 =α 1−1,β0 =α 0,β2 =α 2。
(2) 为了证明两个模型的最小二乘残差相等,即对任何 i i i,有 u i ^ = v ^ i \widehat{u_i}=\widehat{v}_i ui =v i,我们只需要将模型2的误差平方和中的第二个括号展开,然后将模型1和模型2的误差平方和分别代入,得到:
6.考虑下列三个实验步骤:
6.考虑下列三个实验步骤:
(1)对 Y i = β 0 + β 1 X i 1 + β 2 X i 2 + u i Y_i=\beta_0+\beta_1 X_{i1}+\beta_2 X_{i2}+u_i Yi=β0+β1Xi1+β2Xi2+ui进行回归;
(2)对 X i = α 0 + α 1 X i 2 + v i X_i=\alpha_0+\alpha_1 X_{i2}+v_i Xi=α0+α1Xi2+vi进行回归,计算残差 v ^ i \widehat{v}_i v i;
(3)对 Y i = γ 0 + γ 1 v i ^ + γ 2 X i 2 + w i Y_i=\gamma_0+\gamma_1\widehat{v_i}+\gamma_2 X_{i2}+w_i Yi=γ0+γ1vi +γ2Xi2+wi进行回归。
试证明 β 1 ^ = γ 1 ^ \widehat{\beta_1}= \widehat{\gamma_1} β1 =γ1 ,并直观地解释该结果。
首先,我们可以将第一个回归方程重写为 Y i = β 0 + β 1 X i 1 + β 2 X i 2 + ϵ i Y_i = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \epsilon_i Yi=