前言

大家好，我是阿光。

本专栏整理了《图神经网络》，内包含了不同图神经网络的原理以及相关代码实现，详细讲解图神经网络，理论与实践相结合，如GCN、GraphSAGE、GAT等经典图网络，每一个代码实例都附带有完整的代码+数据集。

正在更新中~ ✨

🚨 我的项目环境：

• 平台：Windows10
• 语言环境：python3.7
• 编译器：PyCharm
• PyTorch版本：1.11.0
• PyG版本：2.1.0

💥 项目专栏：【入门图神经网络】

---

一、注意力机制

对于人类来讲，由于人的大脑处理信息能力的局限，所以就需要我们对一些信息的过滤来获取更为重要的信息来帮助我们进行判断，当我们使用眼球看一些东西的时候，我们往往会首先观察到更为显眼的事物，或者是说你现在在看我的博文，眼球一定集中在电脑屏幕上，而你桌面上的其它物体其实你的余光是可以看到的，但是你没有注意到，这都是采用了注意力机制。

对于这个问题，我们人类处理问题常常会把焦点放在更为重要的事情身上，而一定程度忽略一些小事件，这会大大提高人类对于信息处理效率，能够立刻从海量信息中获取与我们目标需要的信息。

比如我们想判断一张图片中的动物是什么，例如上图我们想判断图中的动物是不是企鹅，我们关注的肯定是企鹅本身，目光首先立刻就会定在企鹅身上，而不会过于关注后面的雪地和蓝天，因为我们觉得直接看动物本身对于我们判别动物更为有用，而看背景判别动物不太实用，这是利用了视觉上的注意力机制。

对于文本任务也是一样，我们可能会看上下文的词对当前词的影响，我们会更关注贡献程度最大的词，像Transformer中就是利用了Self-Attention机制，利用Q、K、V来计算注意力分数，这个分数就代表贡献程度或者说是重要程度。

二、Q、K、V

如果要理解注意力机制一定需要理解Q、K、V是什么？

这三个字母分别代表查询向量（Query）、键值向量（Key）、值向量（Value），由于我们需要从信息中获取与我们目标任务重要的信息，那么我们就需要对这些信息计算权重，也就是注意力分数，这个分数代表不同信息对于目标的重要性程度。

那么这个Q可以就是我们的任务向量，K就是其它信息的向量，我们利用Q分别与不同的K进行查询，通过一些方法计算权重（常见是相关性），然后利用这个分数进行权重分配，然后融合信息。

$$Attention(Q,K,V)=\sum _i^L<Q,K_i>V_i$$

上面式子就可以用来表示注意力机制，通过使用我们的目标Q分别与其它K做内积，计算权重分数，然后用这些权重分别乘以对应的V进行信息加权。

这里我们并没有将权重分数归一化，由于要信息加权，一般是要将分数归一化的，保证不同信息的贡献程度之和为1。

对于这个权重分数计算方法有很多，因为我们是要计算权重，它是一个标量，一个数，所以只要是能够是两个向量最终计算结果为一个数的方法都是可行的，但是要符合任务要求，最常见就是做内积操作，或者复杂一点就是将其拼接送入到MLP中进行映射。

三、图注意力网络

说了这么多，应该能够大概了解注意力机制是什么了吧，说白了就是按照一定权重进行信息加权。

对于GCN来将我们最重要的一个阶段就是进行聚合邻居信息，利用邻居的信息来表示自己节点的信息，最常见就是利用邻接矩阵，如果两个节点之间存在边的话，就将其进行聚合，对于GAT（图注意力网络）来将，就是在聚合邻居信息时考虑了不同邻居的权重信息，然后将这些邻居的信息按照注意力分数进行信息加权。

那么如何通过Q、K、V来计算这个聚合后的特征信息呢？

对于GAT中，Q就是我们当前节点的特征向量，而K就是邻居的特征向量，V也是邻居经过W映射后的特征向量，计算注意力分数我们需要拿着自身节点的特征向量分别与邻居节点的特征向量做内积计算分数，然后将分数归一化，然后分别乘以对应的节点特征向量进行加权操作。

1.第一步：计算中心节点与邻居节点的注意力分数（权重）
$$e_{ij}=\varphi (W{h}_i,W{h}_j)$$
该式中 $e_{ij}$ 代表节点i和节点j之间的注意力分数，$\varphi$ 代表计算权重的方法，常用是内积操作，这里可能有点不太一样，上面我们说过是使用Q和K直接相乘，为什么这里多了个W呢？这个W是我们模型需要学的参数，用来将我们原始节点的特征维度映射到一个新的维度上面。

对于本示例中$\varphi$我们使用的是MLP操作，定义一个a向量维度为映射后节点特征维度的2倍，将$W{h}_i$和$W{h}_j$这两个列向量按列进行拼接，然后与a向量进行点乘，计算内积。

2.第二步：激活权重分数

$$e_{i,j}=LeakyReLU(a^T[W{h}_i||W{h}_j])$$
上面的$||$表示向量拼接操作，就是将映射后的列向量进行拼接，将拼接后的向量与a向量做内积操作，然后使用LeakyReLU激活函数进行激活。

3.第三步：权重归一化

由于为了聚合信息进行加权，我们要使所有的权重之和为1。
$$e_{i,j}=softmax(e_{i,j})=\frac{exp(LeakyReLU(a^T[W{h}_i||W{h}_j]))}{{\sum }_{k\in N(i)\cup i}LeakyReLU(a^T[W{h}_i||W{h}_k])}$$

上式中的$k\in N(i)\cup i$ 表示节点i的邻居信息，后面并上i就是在计算注意力分数考虑自身信息。

4.第四步：信息聚合

$$h_i^{{}^{\prime }}=e_{i,i}W{h}_i+\sum _{j\in N(i)}{e}_{i,j}W{h}_j$$

聚合就是将邻居节点特征信息与自身节点特征信息按照一定的权重分数进行加和，形成新的节点表示特征。

对于新的节点的特征维度可以和原来节点的特征维度是不同的，这取决于我们的参数W，W会将信息从原始特征空间d映射到新的空间 $d^{\prime }$，例如原始每个节点的特征向量的维度为3，如果我们的W矩阵的维度为【5，3】，那么W乘以h后，我们的 h’的节点的维度就变成了5。

四、多头注意力网络

多头注意力网络就是使用多个注意力机制形成多个聚合结果，那么为什么要采用这种机制呢？

对于常见卷积网络，当我们使用卷积核提取特征信息时，我们常常会使用多组卷积核去进行提取，目的就是每组卷积核能够提取到不同的图像信息，第一组提取纹理、第二组提取边缘信息等，那么引入多头注意力网络也是这个原因，希望每个注意力机制网络能够注意到不同的内容，进一步提升注意力层的表达能力。

对于最终形成的多组聚合结果，一般是两种处理方式，第一种是将所有的结果取平均或者最大化来获得该节点的最终输出，第二种是将多组输出结果按照列的方式进行拼接，形成【heads*out_channels】形状的输出，例如我们我们使用8组，每组的映射矩阵W的维度为【5，3】，那么每组的输出结果为5维，然后将这8组进行拼接，形成最终的40维。

$$h_i^{{}^{\prime }}=|{|}_{k=1}^K(e_{i,i}W{h}_i+\sum _{j\in N(i)}{e}_{i,j}W{h}_j)$$

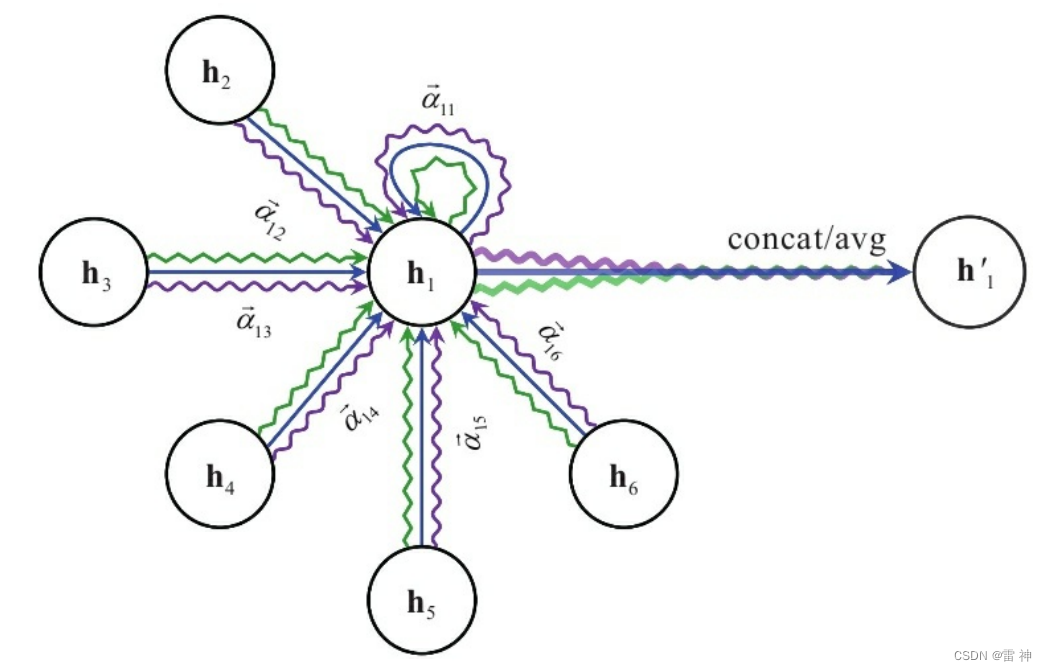
上图中的heads为3，采用了3组注意力机制网络，然后将3组网络的结果进行拼接形成最终的h。

换成公式表示就是：

$$(A\otimes M)XW$$

上式中的A为我们的邻接矩阵或者拉普拉斯矩阵，就是反应节点之间关系的矩阵，M为注意力分数矩阵，对应位置为节点对节点的注意力分数，X就是我们的特征矩阵，W就是学习的参数。