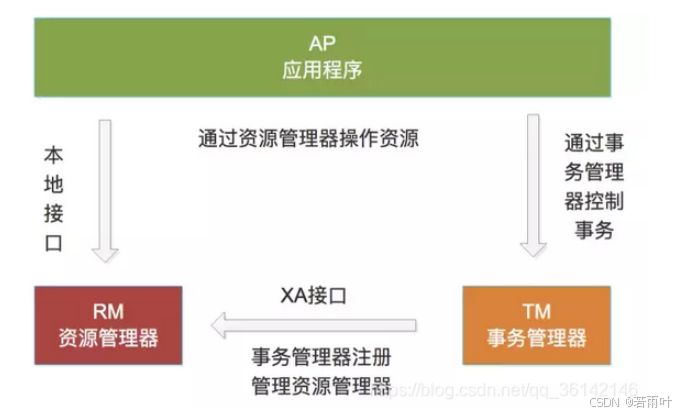
基本思想
先确定待排序数组的最大值(Max)和最小值(Min),随后创建Max - Min + 1个长度的数组称为计数数组,计数数组的索引对应着待排序数组中元素的值,数组的值表示该元素的出现次数。通过从前往后或者从后往前遍历数组,用数组下标+Min得到已排序好数组的值。并且累加每个位置的计数,得到每个元素的最终位置。最后依次将元素放回到结果数组中,得到排序后的数组。
示例
假设我们有以下数组需要排序:[4, 2, 2, 8, 3, 3, 1]
1、确定范围:最大值是 8,最小值是 1。
2、创建计数数组:根据最大值和最小值,创建计数数组 C,其长度为 最大值 - 最小值 + 1,即 C[0] 对应数字 1,C[7] 对应数字 8。
C[0] = 0 (表示数字 1 出现次数)
C[1] = 0 (表示数字 2 出现次数)
C[2] = 0 (表示数字 3 出现次数)
C[3] = 0 (表示数字 4 出现次数)
C[4] = 0 (表示数字 5 出现次数)
C[5] = 0 (表示数字 6 出现次数)
C[6] = 0 (表示数字 7 出现次数)
C[7] = 0 (表示数字 8 出现次数)
3、统计每个数字的出现次数:
C[0] = 1 (数字 1 出现 1 次)
C[1] = 2 (数字 2 出现 2 次)
C[2] = 2 (数字 3 出现 2 次)
C[3] = 1 (数字 4 出现 1 次)
C[7] = 1 (数字 8 出现 1 次)4、累加计数数组:为了确定每个元素的位置,累加每个元素的计数值。
5、将元素放入结果数组:根据累加后的计数数组,将原数组的元素放到排序后的结果数组中。
排序后的结果:[1, 2, 2, 3, 3, 4, 8]
复杂度
时间复杂度:O(n + k),其中 n 是待排序数组的元素个数,k 是待排序数组中的最大值和最小值之间的范围(即最大值Max与最小值Min之差)。
如果数组中的元素范围(k)不大,那么计数排序的时间复杂度可以接近 O(n),适合用于范围较小的整数排序。
如果元素范围 k 很大,计数排序的空间和时间复杂度就会受到影响。
空间复杂度:O(n + k),需要额外的空间来存储计数数组和排序后的数组。
稳定性:计数排序是稳定的。
代码实现
public static void countingSort(int[] arr) {// 1. 找到最大值和最小值int max = Integer.MIN_VALUE;int min = Integer.MAX_VALUE;for (int num : arr) {if (num > max) max = num;if (num < min) min = num;}// 2. 创建计数数组int range = max - min + 1;int[] count = new int[range];// 3. 统计每个元素的出现次数for (int num : arr) {count[num - min]++;}// 4. 累加计数数组for (int i = 1; i < count.length; i++) {count[i] += count[i - 1];}// 5. 构造排序后的数组int[] sortedArr2 = new int[arr.length];for (int i = arr.length - 1; i >= 0; i--) {sortedArr2[count[arr[i] - min] - 1] = arr[i];count[arr[i] - min]--;}// 6. 将排序后的数组复制回原数组System.arraycopy(sortedArr, 0, arr, 0, arr.length);} 这段代码是简化版的累加计数过程,可以代替上段代码的4-5步,适用于重复元素出现过多的情况int[] sortedArr = new int[arr.length];int j = 0;for (int i = 0; i <= arr.length - 1; i++) {while(count[j] == 0){j++;}sortedArr[i] = j + min;count[j]--;}