混沌反馈共享和群体协同效应的蝴蝶优化算法
文章目录
- 混沌反馈共享和群体协同效应的蝴蝶优化算法
- 1.蝴蝶优化算法
- 2. 改进蝴蝶优化算法
- 2.1 Hénon混沌映射
- 2.2 反馈共享机制
- 2.3 群体协同效应位置更新机制
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.Python代码
摘要:针对蝴蝶优化算法寻优精度低和易陷入局部最优等缺点,提出了混沌反馈共享和群体协同效应的蝴蝶优化算法。首先,利用Hénon混沌初始化种群,能够使种群尽可能的覆盖搜索盲区,增加种群多样性,提高算法寻优性能;其次,利用反馈控制电路中正负反馈作用机制的思想,构建蝴蝶之间的反馈共享交流网络,使得蝴蝶个体能够接收来自多个方向的信息帮助种群定位最优解的位置并执行精细搜索,增强算法逃离局部最优的能力和加快算法收敛的速度;最后,利用群体协同效应机制,提高和平衡全局与局部搜索的能力,增强算法的全局和局部的寻优能力。
1.蝴蝶优化算法
基础蝴蝶优化算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107855860
2. 改进蝴蝶优化算法
2.1 Hénon混沌映射
利用 Hénon 的混沌序列分布更加均匀的特点,种群可以最大程度覆盖搜索盲区,增加蝴蝶个体的多样性,从一定程度上帮助算法跳出局部极值,迚而增强算法寻优的能力。因此,本文采用 Hénon 混沌映射初始化蝴蝶种群。其数学描述:
{ x ( k ) = 1 − γ ( x ( k − 1 ) ) 2 + φ y ( k − 1 ) y ( k ) = x ( k − 1 ) (8) \left\{\begin{array}{l} x(k)=1-\gamma(x(k-1))^{2}+\varphi y(k-1) \\ y(k)=x(k-1) \end{array}\right.\tag{8} {x(k)=1−γ(x(k−1))2+φy(k−1)y(k)=x(k−1)(8)
z i k = x i k − φ i γ i − φ i , i = 1 , 2 , ⋯ N (9) z_{i}^{k}=\frac{x_{i}^{k}-\varphi_{i}}{\gamma_{i}-\varphi_{i}}, i=1,2, \cdots \mathrm{N} \tag{9} zik=γi−φixik−φi,i=1,2,⋯N(9)
式(8)中, γ = 1.4 , φ = 0.3 , x ( 0 ) = 0 \gamma=1.4, \varphi=0.3, \quad x(0)=0 γ=1.4,φ=0.3,x(0)=0 , y ( 0 ) = 0 , k y(0)=0 , k y(0)=0,k 代表混沌迭代次籹, k ≤ N k \leq N k≤N 。为 了砬开 Hénon 映射的不动点, 以兰全最优解 x i ∗ = x i k , l b i ≤ x i ∗ ≤ u b i x_{i}^{*}=x_{i}^{k}, l b_{i} \leq x_{i}^{*} \leq u b_{i} xi∗=xik,lbi≤xi∗≤ubi 为衤刃始值, 选取 n n n 个微 小丟异的初始值, 通过式 ( 8 ) (8) (8) 产主 [ 0 , 1 ] [0,1] [0,1] 区间上 n n n 个不同的混沌序列式(9),最厉通过逆映射 得到个体搜索空间变量 x i ′ x_{i}^{\prime} xi′ :
x i t = l b i + z i k ( u b i − l b i ) (10) x_{i}^{t}=l b_{i}+z_{i}^{k}\left(u b_{i}-l b_{i}\right)\tag{10} xit=lbi+zik(ubi−lbi)(10)
其中, z i k z_{i}^{k} zik 是最优混沌变量, [ 1 b i , u b i ] \left[1 b_{i}, u b_{i}\right] [1bi,ubi] 是 x i t x_{i}^{t} xit 搜索空间的上、下界。
2.2 反馈共享机制
如果食物源被证实存在于两只蝴蝶的 周围, 通过正反馈作用当前蝴蝶会移动到两 只蝴蝶周围。如果不是, 通过负反馈作用它 向最好的蝴蝶移动。数学模型描述如下:
α = ( F max − F min ) r 3 + F min (11) \alpha=\left(F_{\max }-F_{\min }\right) r_{3}+F_{\text {min }} \tag{11} α=(Fmax−Fmin)r3+Fmin (11)
θ = 1 1 + exp ( − λ ) (12) \theta=\frac{1}{1+\exp (-\lambda)} \tag{12} θ=1+exp(−λ)1(12)
x i ′ = { x i ′ + ( g ′ − x i t ) α + ( x h t − x i ′ ) α + θ F ( x h t ) < F ( x i t ) x i ′ + ( g − x i ′ ) α + θ F ( x h ′ ) ≥ F ( x i ′ ) (13) \begin{gathered} x_{i}^{\prime}= \begin{cases}x_{i}^{\prime}+\left(g^{\prime}-x_{i}^{t}\right) \alpha+ \\ \left(x_{h}^{t}-x_{i}^{\prime}\right) \alpha+\theta & F\left(x_{h}^{t}\right)<F\left(x_{i}^{t}\right) \\ x_{i}^{\prime}+\left(g-x_{i}^{\prime}\right) \alpha+\theta & F\left(x_{h}^{\prime}\right) \geq F\left(x_{i}^{\prime}\right)\end{cases} \end{gathered}\tag{13} xi′=⎩ ⎨ ⎧xi′+(g′−xit)α+(xht−xi′)α+θxi′+(g−xi′)α+θF(xht)<F(xit)F(xh′)≥F(xi′)(13)
这里 α \alpha α 为共享系数, F max 、 F min F_{\text {max }} 、 F_{\text {min }} Fmax 、Fmin 分别为 种群最大、最小适应度值, r 3 r_{3} r3 是 [ 0 , 1 ] [0,1] [0,1] 之间的 随机数, θ \theta θ 是反馈因子, 能够加速蝴蝶之间 的信息反馈速率实现信息快速共享, 其中 λ \lambda λ 表示当前迭代个体数, x h ′ x_{h}^{\prime} xh′ 表示随机蝴蝶的 位置, F F F 表示计算适应度。香味反馈机制使得蝴蝶个体可以更多的围绕最佳位置迚行挖掘,同时式(13)中提出的飞行方向使蝴蝶个体运动方向具有多样性化的能力,可以增强探索能力,特别是在迭代的初始阶段,可以避克过早收敛。
2.3 群体协同效应位置更新机制
其一利用了黄全分割数不需要梯度信 息的优点, 对标准 BOA 算法的距离公式进 行改进; 其二, 群体协同效应主要由个体矫 正因子和群体协调因子构成, 其利用了正弦 曲线值域分布特点, 具体如下:
τ = 5 − 1 2 (14) \tau=\frac{\sqrt{5}-1}{2} \tag{14} τ=25−1(14)
l 1 = − π + 2 π ( 1 − τ ) (15) l_{1}=-\pi+2 \pi(1-\tau) \tag{15} l1=−π+2π(1−τ)(15)
l 2 = − π + 2 π τ (16) \begin{gathered} l_{2}=-\pi+2 \pi \tau \end{gathered}\tag{16} l2=−π+2πτ(16)
新局部搜索公式:
d i s 1 ′ = ∣ l 1 x j ′ − l 2 x i ′ ∣ (17) d i s_{1}^{\prime}=\left|l_{1} x_{j}^{\prime}-l_{2} x_{i}^{\prime}\right| \tag{17} dis1′=∣ ∣l1xj′−l2xi′∣ ∣(17)
x i t + 1 = x i ′ ∣ sin ( ψ 1 ) ∣ + d i s 1 ′ f i ψ 2 sin ( ψ 1 ) (18) \begin{gathered} x_{i}^{t+1}=x_{i}^{\prime}\left|\sin \left(\psi_{1}\right)\right|+d i s_{1}^{\prime} f_{i} \psi_{2} \sin \left(\psi_{1}\right) \end{gathered}\tag{18} xit+1=xi′∣sin(ψ1)∣+dis1′fiψ2sin(ψ1)(18)
新全局搜索公式:
d i s 2 ′ = ∣ l 1 g − l 2 x i t ∣ (19) d i s_{2}^{\prime}=\left|l_{1} g-l_{2} x_{i}^{t}\right| \tag{19} dis2′=∣ ∣l1g−l2xit∣ ∣(19)
x i t + 1 = x i t ∣ sin ( ψ 1 ) ∣ + d i s 2 f i ψ 2 sin ( ψ 1 ) (20) \begin{gathered} x_{i}^{t+1}=x_{i}^{t}\left|\sin \left(\psi_{1}\right)\right|+d i s_{2} f_{i} \psi_{2} \sin \left(\psi_{1}\right) \end{gathered} \tag{20} xit+1=xit∣sin(ψ1)∣+dis2fiψ2sin(ψ1)(20)
其中, τ \tau τ 是黄金分割数, l 1 、 l 2 l_{1} 、 l_{2} l1、l2 是具备 黄金分割数优点的距离更新系数, 在两只蝴 蝶相互作用时获得巨大利益, 提高算法收敛 速度。disis 、dis~是新的距离公式, ψ , ∈ [ 0 , π ] \psi, \in[0, \pi] ψ,∈[0,π], ψ 2 ∈ [ 0 , 2 π ] \psi_{2} \in[0,2 \pi] ψ2∈[0,2π] 的随机数。
式 (18),(20) 增加了个体矫正因子 ∣ sin ( ψ 1 ) ∣ \left|\sin \left(\psi_{1}\right)\right| ∣sin(ψ1)∣ 的波动范围是 [ 0 , 1 2 ] \left[0, \frac{1}{2}\right] [0,21], 从个体层面指 引个体飞行调整; 群体协调因子 ψ 2 sin ( ψ 1 ) \psi_{2} \sin \left(\psi_{1}\right) ψ2sin(ψ1) 的浮动范围是 [ − 2 π , 2 π ] [-2 \pi, 2 \pi] [−2π,2π], 从群体层面指引种群 搜索方向, 两者协同配合使得蝴蝶种群向着 食物源位置搜索。与原来的位置更新公式(5)、 (6)相比, 加人了个体矫正因子、群体协调因 子能够更好的指引蝴蝶从原位置到食物源 位置附近, 更利于保持种群多样性, 进而增 强全局搜索能力。
综上三节, 利用混沌初始化种群, 使得 种群分布更加均匀, 为后续算法寻优打下基 础。通过反馈共享, 引人随机蝴蝶加快蝴蝶 种群之间的信息交流实现信息流动达到共 享, 增强算法跳出局部最优能力。引人群体 协同, 降低蝴蝶的盲目依赖性, 增强及平衡 全局和局部搜索能力。寻优过程中, 蝴蝶种 群能够进行针对性的搜索, 调整适合个体进 化方向, 进而增强算法寻优能力。

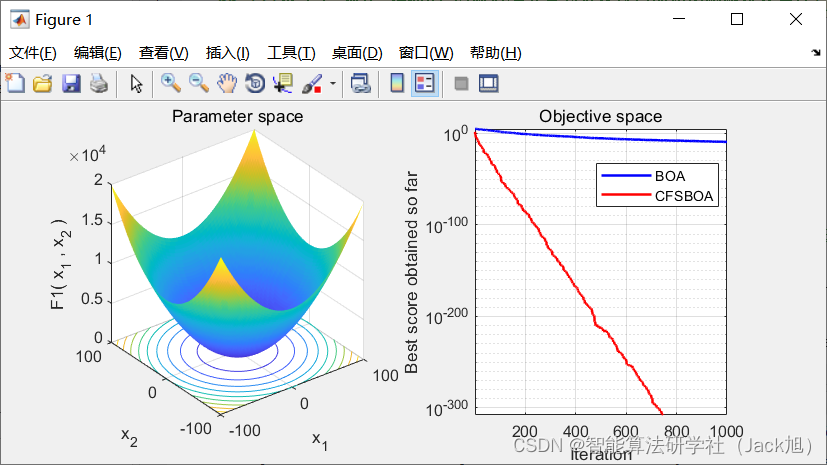
3.实验结果
4.参考文献
[1]李守玉,何庆,杜逆索.混沌反馈共享和群体协同效应的蝴蝶优化算法[J/OL].计算机科学与探索:1-12[2021-04-30].http://kns.cnki.net/kcms/detail/11.5602.TP.20210128.1109.014.html.