信用卡欺诈检测
信用卡欺诈检测是kaggle上一个项目,数据来源是2013年欧洲持有信用卡的交易数据,详细内容见https://www.kaggle.com/mlg-ulb/creditcardfraud
这个项目所要实现的目标是对一个交易预测它是否存在信用卡欺诈,和大部分机器学习项目的区别在于正负样本的不均衡,而且是极不均衡的,所以这是特征工程需要处理的第一个问题。
除此之外,在数据预处理上减轻的负担是缺失值的处理,并且大多数特征是经过了均值化处理的。
项目背景与数据初探
# 导入基础的库,其他的模型库在需要时再导入
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
# 设置显示的宽度,避免有过长行不显示的问题
pd.set_option('display.max_columns', 10000)
pd.set_option('display.max_colwidth', 10000)
pd.set_option('display.width', 10000)
# 导入数据并查看基本数据情况
data = pd.read_csv('D:/数据分析/kaggle/信用卡欺诈/creditcard.csv')
data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 284807 entries, 0 to 284806
Data columns (total 31 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 Time 284807 non-null float641 V1 284807 non-null float642 V2 284807 non-null float643 V3 284807 non-null float644 V4 284807 non-null float645 V5 284807 non-null float646 V6 284807 non-null float647 V7 284807 non-null float648 V8 284807 non-null float649 V9 284807 non-null float6410 V10 284807 non-null float6411 V11 284807 non-null float6412 V12 284807 non-null float6413 V13 284807 non-null float6414 V14 284807 non-null float6415 V15 284807 non-null float6416 V16 284807 non-null float6417 V17 284807 non-null float6418 V18 284807 non-null float6419 V19 284807 non-null float6420 V20 284807 non-null float6421 V21 284807 non-null float6422 V22 284807 non-null float6423 V23 284807 non-null float6424 V24 284807 non-null float6425 V25 284807 non-null float6426 V26 284807 non-null float6427 V27 284807 non-null float6428 V28 284807 non-null float6429 Amount 284807 non-null float6430 Class 284807 non-null int64
dtypes: float64(30), int64(1)
memory usage: 67.4 MB
data.shape
(284807, 31)
data.describe()
| Time | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 | V17 | V18 | V19 | V20 | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Amount | Class | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 284807.000000 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 2.848070e+05 | 284807.000000 | 284807.000000 |
| mean | 94813.859575 | 3.919560e-15 | 5.688174e-16 | -8.769071e-15 | 2.782312e-15 | -1.552563e-15 | 2.010663e-15 | -1.694249e-15 | -1.927028e-16 | -3.137024e-15 | 1.768627e-15 | 9.170318e-16 | -1.810658e-15 | 1.693438e-15 | 1.479045e-15 | 3.482336e-15 | 1.392007e-15 | -7.528491e-16 | 4.328772e-16 | 9.049732e-16 | 5.085503e-16 | 1.537294e-16 | 7.959909e-16 | 5.367590e-16 | 4.458112e-15 | 1.453003e-15 | 1.699104e-15 | -3.660161e-16 | -1.206049e-16 | 88.349619 | 0.001727 |
| std | 47488.145955 | 1.958696e+00 | 1.651309e+00 | 1.516255e+00 | 1.415869e+00 | 1.380247e+00 | 1.332271e+00 | 1.237094e+00 | 1.194353e+00 | 1.098632e+00 | 1.088850e+00 | 1.020713e+00 | 9.992014e-01 | 9.952742e-01 | 9.585956e-01 | 9.153160e-01 | 8.762529e-01 | 8.493371e-01 | 8.381762e-01 | 8.140405e-01 | 7.709250e-01 | 7.345240e-01 | 7.257016e-01 | 6.244603e-01 | 6.056471e-01 | 5.212781e-01 | 4.822270e-01 | 4.036325e-01 | 3.300833e-01 | 250.120109 | 0.041527 |
| min | 0.000000 | -5.640751e+01 | -7.271573e+01 | -4.832559e+01 | -5.683171e+00 | -1.137433e+02 | -2.616051e+01 | -4.355724e+01 | -7.321672e+01 | -1.343407e+01 | -2.458826e+01 | -4.797473e+00 | -1.868371e+01 | -5.791881e+00 | -1.921433e+01 | -4.498945e+00 | -1.412985e+01 | -2.516280e+01 | -9.498746e+00 | -7.213527e+00 | -5.449772e+01 | -3.483038e+01 | -1.093314e+01 | -4.480774e+01 | -2.836627e+00 | -1.029540e+01 | -2.604551e+00 | -2.256568e+01 | -1.543008e+01 | 0.000000 | 0.000000 |
| 25% | 54201.500000 | -9.203734e-01 | -5.985499e-01 | -8.903648e-01 | -8.486401e-01 | -6.915971e-01 | -7.682956e-01 | -5.540759e-01 | -2.086297e-01 | -6.430976e-01 | -5.354257e-01 | -7.624942e-01 | -4.055715e-01 | -6.485393e-01 | -4.255740e-01 | -5.828843e-01 | -4.680368e-01 | -4.837483e-01 | -4.988498e-01 | -4.562989e-01 | -2.117214e-01 | -2.283949e-01 | -5.423504e-01 | -1.618463e-01 | -3.545861e-01 | -3.171451e-01 | -3.269839e-01 | -7.083953e-02 | -5.295979e-02 | 5.600000 | 0.000000 |
| 50% | 84692.000000 | 1.810880e-02 | 6.548556e-02 | 1.798463e-01 | -1.984653e-02 | -5.433583e-02 | -2.741871e-01 | 4.010308e-02 | 2.235804e-02 | -5.142873e-02 | -9.291738e-02 | -3.275735e-02 | 1.400326e-01 | -1.356806e-02 | 5.060132e-02 | 4.807155e-02 | 6.641332e-02 | -6.567575e-02 | -3.636312e-03 | 3.734823e-03 | -6.248109e-02 | -2.945017e-02 | 6.781943e-03 | -1.119293e-02 | 4.097606e-02 | 1.659350e-02 | -5.213911e-02 | 1.342146e-03 | 1.124383e-02 | 22.000000 | 0.000000 |
| 75% | 139320.500000 | 1.315642e+00 | 8.037239e-01 | 1.027196e+00 | 7.433413e-01 | 6.119264e-01 | 3.985649e-01 | 5.704361e-01 | 3.273459e-01 | 5.971390e-01 | 4.539234e-01 | 7.395934e-01 | 6.182380e-01 | 6.625050e-01 | 4.931498e-01 | 6.488208e-01 | 5.232963e-01 | 3.996750e-01 | 5.008067e-01 | 4.589494e-01 | 1.330408e-01 | 1.863772e-01 | 5.285536e-01 | 1.476421e-01 | 4.395266e-01 | 3.507156e-01 | 2.409522e-01 | 9.104512e-02 | 7.827995e-02 | 77.165000 | 0.000000 |
| max | 172792.000000 | 2.454930e+00 | 2.205773e+01 | 9.382558e+00 | 1.687534e+01 | 3.480167e+01 | 7.330163e+01 | 1.205895e+02 | 2.000721e+01 | 1.559499e+01 | 2.374514e+01 | 1.201891e+01 | 7.848392e+00 | 7.126883e+00 | 1.052677e+01 | 8.877742e+00 | 1.731511e+01 | 9.253526e+00 | 5.041069e+00 | 5.591971e+00 | 3.942090e+01 | 2.720284e+01 | 1.050309e+01 | 2.252841e+01 | 4.584549e+00 | 7.519589e+00 | 3.517346e+00 | 3.161220e+01 | 3.384781e+01 | 25691.160000 | 1.000000 |
data.head().append(data.tail())
| Time | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 | V17 | V18 | V19 | V20 | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Amount | Class | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | -1.359807 | -0.072781 | 2.536347 | 1.378155 | -0.338321 | 0.462388 | 0.239599 | 0.098698 | 0.363787 | 0.090794 | -0.551600 | -0.617801 | -0.991390 | -0.311169 | 1.468177 | -0.470401 | 0.207971 | 0.025791 | 0.403993 | 0.251412 | -0.018307 | 0.277838 | -0.110474 | 0.066928 | 0.128539 | -0.189115 | 0.133558 | -0.021053 | 149.62 | 0 |
| 1 | 0.0 | 1.191857 | 0.266151 | 0.166480 | 0.448154 | 0.060018 | -0.082361 | -0.078803 | 0.085102 | -0.255425 | -0.166974 | 1.612727 | 1.065235 | 0.489095 | -0.143772 | 0.635558 | 0.463917 | -0.114805 | -0.183361 | -0.145783 | -0.069083 | -0.225775 | -0.638672 | 0.101288 | -0.339846 | 0.167170 | 0.125895 | -0.008983 | 0.014724 | 2.69 | 0 |
| 2 | 1.0 | -1.358354 | -1.340163 | 1.773209 | 0.379780 | -0.503198 | 1.800499 | 0.791461 | 0.247676 | -1.514654 | 0.207643 | 0.624501 | 0.066084 | 0.717293 | -0.165946 | 2.345865 | -2.890083 | 1.109969 | -0.121359 | -2.261857 | 0.524980 | 0.247998 | 0.771679 | 0.909412 | -0.689281 | -0.327642 | -0.139097 | -0.055353 | -0.059752 | 378.66 | 0 |
| 3 | 1.0 | -0.966272 | -0.185226 | 1.792993 | -0.863291 | -0.010309 | 1.247203 | 0.237609 | 0.377436 | -1.387024 | -0.054952 | -0.226487 | 0.178228 | 0.507757 | -0.287924 | -0.631418 | -1.059647 | -0.684093 | 1.965775 | -1.232622 | -0.208038 | -0.108300 | 0.005274 | -0.190321 | -1.175575 | 0.647376 | -0.221929 | 0.062723 | 0.061458 | 123.50 | 0 |
| 4 | 2.0 | -1.158233 | 0.877737 | 1.548718 | 0.403034 | -0.407193 | 0.095921 | 0.592941 | -0.270533 | 0.817739 | 0.753074 | -0.822843 | 0.538196 | 1.345852 | -1.119670 | 0.175121 | -0.451449 | -0.237033 | -0.038195 | 0.803487 | 0.408542 | -0.009431 | 0.798278 | -0.137458 | 0.141267 | -0.206010 | 0.502292 | 0.219422 | 0.215153 | 69.99 | 0 |
| 284802 | 172786.0 | -11.881118 | 10.071785 | -9.834783 | -2.066656 | -5.364473 | -2.606837 | -4.918215 | 7.305334 | 1.914428 | 4.356170 | -1.593105 | 2.711941 | -0.689256 | 4.626942 | -0.924459 | 1.107641 | 1.991691 | 0.510632 | -0.682920 | 1.475829 | 0.213454 | 0.111864 | 1.014480 | -0.509348 | 1.436807 | 0.250034 | 0.943651 | 0.823731 | 0.77 | 0 |
| 284803 | 172787.0 | -0.732789 | -0.055080 | 2.035030 | -0.738589 | 0.868229 | 1.058415 | 0.024330 | 0.294869 | 0.584800 | -0.975926 | -0.150189 | 0.915802 | 1.214756 | -0.675143 | 1.164931 | -0.711757 | -0.025693 | -1.221179 | -1.545556 | 0.059616 | 0.214205 | 0.924384 | 0.012463 | -1.016226 | -0.606624 | -0.395255 | 0.068472 | -0.053527 | 24.79 | 0 |
| 284804 | 172788.0 | 1.919565 | -0.301254 | -3.249640 | -0.557828 | 2.630515 | 3.031260 | -0.296827 | 0.708417 | 0.432454 | -0.484782 | 0.411614 | 0.063119 | -0.183699 | -0.510602 | 1.329284 | 0.140716 | 0.313502 | 0.395652 | -0.577252 | 0.001396 | 0.232045 | 0.578229 | -0.037501 | 0.640134 | 0.265745 | -0.087371 | 0.004455 | -0.026561 | 67.88 | 0 |
| 284805 | 172788.0 | -0.240440 | 0.530483 | 0.702510 | 0.689799 | -0.377961 | 0.623708 | -0.686180 | 0.679145 | 0.392087 | -0.399126 | -1.933849 | -0.962886 | -1.042082 | 0.449624 | 1.962563 | -0.608577 | 0.509928 | 1.113981 | 2.897849 | 0.127434 | 0.265245 | 0.800049 | -0.163298 | 0.123205 | -0.569159 | 0.546668 | 0.108821 | 0.104533 | 10.00 | 0 |
| 284806 | 172792.0 | -0.533413 | -0.189733 | 0.703337 | -0.506271 | -0.012546 | -0.649617 | 1.577006 | -0.414650 | 0.486180 | -0.915427 | -1.040458 | -0.031513 | -0.188093 | -0.084316 | 0.041333 | -0.302620 | -0.660377 | 0.167430 | -0.256117 | 0.382948 | 0.261057 | 0.643078 | 0.376777 | 0.008797 | -0.473649 | -0.818267 | -0.002415 | 0.013649 | 217.00 | 0 |
data.Class.value_counts()
0 284315
1 492
Name: Class, dtype: int64
- 数据包含284807样本,30个属性特征和一个所属类别,数据完整没有缺失值,所以不需要缺失值的处理。非匿名特征包括时间和交易金额,以及所属的类别,匿名特征28个从v1-v28,统计上的均值(基本上等于0)和方差(1左右)可以看出是已经进行了归一化处理。(在Kaggle上的介绍说:匿名特征是经过了脱敏和PCA处理的,时间特征Time包含数据集中每个交易和第一个交易之间经过的秒数,应该是距离开始采集数据的时间,总共是两天,172792正好是差不多48小时)
- 正负样本不均衡的问题,从描述性统计结果上的class列,均值为0.001727,说明极大多数样本都是0,也可以通过data.value_counts()查看,正常交易284315项,而异常的只有492项,这种极不平衡的样本处理将是特征工程的主要任务
探索性数据分析(EDA)
* 单一属性分析
数据属性都是数值型,所以不需要区分数值属性和类别属性,也不需要对类别属性的重新编码,下面分析单一属性的特点,从预测类别开始
通过类别的分布图以及峰度、偏度的计算,可以更直观的看到样本分布的不均衡
# 欺诈与非欺诈类别分布的直方图
sns.countplot('Class', data=data, color='blue')
plt.xlabel('values')
plt.ylabel('Counts')
plt.title('Class Distributions \n (0: No Fraud || 1: Fraud)')
Text(0.5, 1.0, 'Class Distributions \n (0: No Fraud || 1: Fraud)')

print('Kurtosis:', data.Class.kurt())
print('Skewness:', data.Class.skew())
Kurtosis: 573.887842782971
Skewness: 23.99757931064749
下面分析两个没有经过标准化的属性:Time和Amount
# 数值属性时间与金额分布图,金额用正态分布和对数分布两种方式拟合
import scipy.stats as st
fig, ax = plt.subplots(1, 3, figsize=(18, 4))
print(ax)
sns.distplot(data.Amount, color='blue', ax=ax[0],kde = False,fit=st.norm)
ax[0].set_title('Distribution of transaction amount_normal')sns.distplot(data.Amount,color='blue',ax=ax[1],fit=st.lognorm)
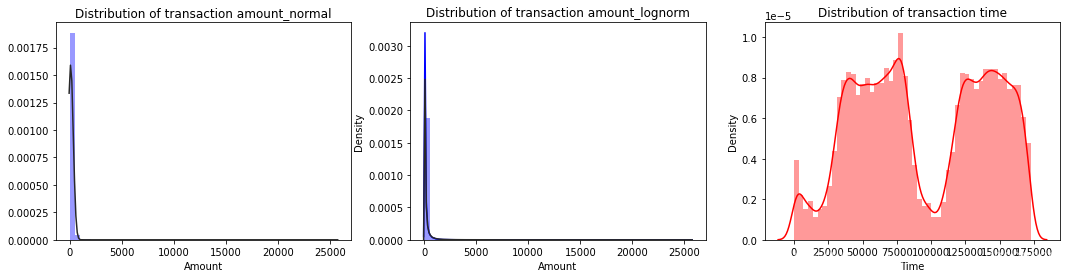
ax[1].set_title('Distribution of transaction amount_lognorm')sns.distplot(data.Time, color='r', ax=ax[2])
ax[2].set_title('Distribution of transaction time')
print(data.Amount.value_counts())
1.00 13688
1.98 6044
0.89 4872
9.99 4747
15.00 3280...
192.63 1
218.84 1
195.52 1
793.50 1
1080.06 1
Name: Amount, Length: 32767, dtype: int64
print('the ratio of Amount<5:', data.Amount[data.Amount < 5].value_counts(
).sum()/data.Amount.value_counts().sum())
print('the ratio of Amount<10:', data.Amount[data.Amount < 10].value_counts(
).sum()/data.Amount.value_counts().sum())
print('the ratio of Amount<20:', data.Amount[data.Amount < 20].value_counts(
).sum()/data.Amount.value_counts().sum())
print('the ratio of Amount<30:', data.Amount[data.Amount < 30].value_counts(
).sum()/data.Amount.value_counts().sum())
print('the ratio of Amount<50:', data.Amount[data.Amount < 50].value_counts(
).sum()/data.Amount.value_counts().sum())
print('the ratio of Amount<100:', data.Amount[data.Amount < 100].value_counts(
).sum()/data.Amount.value_counts().sum())
print('the ratio of Amount>5000:', data.Amount[data.Amount > 5000].value_counts(
).sum()/data.Amount.value_counts().sum())
the ratio of Amount<5: 0.2368726892246328
the ratio of Amount<10: 0.3416840175978821
the ratio of Amount<20: 0.481476929991187
the ratio of Amount<30: 0.562022703093674
the ratio of Amount<50: 0.6660791342909409
the ratio of Amount<100: 0.7985126770058321
the ratio of Amount>5000: 0.00019311323106524768
在金额属性上,绝大多数金额都是小于50美元较小的,存在少量的较大数值如1080美元;时间上在15000s和100000s附近出现了两次低峰,距离开始采样数据的时间分别是4小时和27小时,猜测这时候是凌晨3、4点,这也符合现实,毕竟深夜购物的人还是少数。由于其他的匿名属性都进行了均值化处理,并且金额的拟合效果正态分布优于取对数,下面也将金额Amount进行标准化处理,同样的,时间转化为小时之后再作均值化处理。
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
data['Amount'] = sc.fit_transform(data.Amount.values.reshape(-1, 1))
# reshape()函数的两个参数,-1表示不知道多少行,1表示一列
data['Hour'] = data.Time.apply(lambda x: divmod(x, 3600)[0])
data['Hour'] = data.Hour.apply(lambda x: divmod(x, 24)[1])
# 时间进一步转换成24小时制,因为考虑到交易密度的周期性分布
data['Hour'] = sc.fit_transform(data['Hour'].values.reshape(-1, 1))
data.drop(columns='Time', inplace=True)
data.head().append(data.tail())
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 | V17 | V18 | V19 | V20 | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Amount | Class | Hour | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -1.359807 | -0.072781 | 2.536347 | 1.378155 | -0.338321 | 0.462388 | 0.239599 | 0.098698 | 0.363787 | 0.090794 | -0.551600 | -0.617801 | -0.991390 | -0.311169 | 1.468177 | -0.470401 | 0.207971 | 0.025791 | 0.403993 | 0.251412 | -0.018307 | 0.277838 | -0.110474 | 0.066928 | 0.128539 | -0.189115 | 0.133558 | -0.021053 | 0.244964 | 0 | -2.40693 |
| 1 | 1.191857 | 0.266151 | 0.166480 | 0.448154 | 0.060018 | -0.082361 | -0.078803 | 0.085102 | -0.255425 | -0.166974 | 1.612727 | 1.065235 | 0.489095 | -0.143772 | 0.635558 | 0.463917 | -0.114805 | -0.183361 | -0.145783 | -0.069083 | -0.225775 | -0.638672 | 0.101288 | -0.339846 | 0.167170 | 0.125895 | -0.008983 | 0.014724 | -0.342475 | 0 | -2.40693 |
| 2 | -1.358354 | -1.340163 | 1.773209 | 0.379780 | -0.503198 | 1.800499 | 0.791461 | 0.247676 | -1.514654 | 0.207643 | 0.624501 | 0.066084 | 0.717293 | -0.165946 | 2.345865 | -2.890083 | 1.109969 | -0.121359 | -2.261857 | 0.524980 | 0.247998 | 0.771679 | 0.909412 | -0.689281 | -0.327642 | -0.139097 | -0.055353 | -0.059752 | 1.160686 | 0 | -2.40693 |
| 3 | -0.966272 | -0.185226 | 1.792993 | -0.863291 | -0.010309 | 1.247203 | 0.237609 | 0.377436 | -1.387024 | -0.054952 | -0.226487 | 0.178228 | 0.507757 | -0.287924 | -0.631418 | -1.059647 | -0.684093 | 1.965775 | -1.232622 | -0.208038 | -0.108300 | 0.005274 | -0.190321 | -1.175575 | 0.647376 | -0.221929 | 0.062723 | 0.061458 | 0.140534 | 0 | -2.40693 |
| 4 | -1.158233 | 0.877737 | 1.548718 | 0.403034 | -0.407193 | 0.095921 | 0.592941 | -0.270533 | 0.817739 | 0.753074 | -0.822843 | 0.538196 | 1.345852 | -1.119670 | 0.175121 | -0.451449 | -0.237033 | -0.038195 | 0.803487 | 0.408542 | -0.009431 | 0.798278 | -0.137458 | 0.141267 | -0.206010 | 0.502292 | 0.219422 | 0.215153 | -0.073403 | 0 | -2.40693 |
| 284802 | -11.881118 | 10.071785 | -9.834783 | -2.066656 | -5.364473 | -2.606837 | -4.918215 | 7.305334 | 1.914428 | 4.356170 | -1.593105 | 2.711941 | -0.689256 | 4.626942 | -0.924459 | 1.107641 | 1.991691 | 0.510632 | -0.682920 | 1.475829 | 0.213454 | 0.111864 | 1.014480 | -0.509348 | 1.436807 | 0.250034 | 0.943651 | 0.823731 | -0.350151 | 0 | 1.53423 |
| 284803 | -0.732789 | -0.055080 | 2.035030 | -0.738589 | 0.868229 | 1.058415 | 0.024330 | 0.294869 | 0.584800 | -0.975926 | -0.150189 | 0.915802 | 1.214756 | -0.675143 | 1.164931 | -0.711757 | -0.025693 | -1.221179 | -1.545556 | 0.059616 | 0.214205 | 0.924384 | 0.012463 | -1.016226 | -0.606624 | -0.395255 | 0.068472 | -0.053527 | -0.254117 | 0 | 1.53423 |
| 284804 | 1.919565 | -0.301254 | -3.249640 | -0.557828 | 2.630515 | 3.031260 | -0.296827 | 0.708417 | 0.432454 | -0.484782 | 0.411614 | 0.063119 | -0.183699 | -0.510602 | 1.329284 | 0.140716 | 0.313502 | 0.395652 | -0.577252 | 0.001396 | 0.232045 | 0.578229 | -0.037501 | 0.640134 | 0.265745 | -0.087371 | 0.004455 | -0.026561 | -0.081839 | 0 | 1.53423 |
| 284805 | -0.240440 | 0.530483 | 0.702510 | 0.689799 | -0.377961 | 0.623708 | -0.686180 | 0.679145 | 0.392087 | -0.399126 | -1.933849 | -0.962886 | -1.042082 | 0.449624 | 1.962563 | -0.608577 | 0.509928 | 1.113981 | 2.897849 | 0.127434 | 0.265245 | 0.800049 | -0.163298 | 0.123205 | -0.569159 | 0.546668 | 0.108821 | 0.104533 | -0.313249 | 0 | 1.53423 |
| 284806 | -0.533413 | -0.189733 | 0.703337 | -0.506271 | -0.012546 | -0.649617 | 1.577006 | -0.414650 | 0.486180 | -0.915427 | -1.040458 | -0.031513 | -0.188093 | -0.084316 | 0.041333 | -0.302620 | -0.660377 | 0.167430 | -0.256117 | 0.382948 | 0.261057 | 0.643078 | 0.376777 | 0.008797 | -0.473649 | -0.818267 | -0.002415 | 0.013649 | 0.514355 | 0 | 1.53423 |
# 将样本顺序打乱,因为Hour属性是有顺序的,为后期样本训练集测试集的划分做准备
data = data.sample(frac=1)
data.head().append(data.tail())
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 | V17 | V18 | V19 | V20 | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Amount | Class | Hour | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 107216 | 1.324299 | -1.085563 | 0.237279 | -1.479829 | -1.161581 | -0.372790 | -0.742945 | -0.049038 | -2.376563 | 1.516249 | 1.631516 | 0.137025 | 0.627911 | 0.049387 | 0.025037 | -0.532986 | 0.575155 | -0.556925 | -0.065486 | -0.214061 | -0.526897 | -1.342434 | 0.251389 | -0.065977 | -0.029430 | -0.636325 | 0.020683 | 0.022199 | -0.055132 | 0 | 0.848811 |
| 168047 | -0.216830 | 0.175845 | -0.126917 | 0.116160 | 3.348383 | 4.292672 | 0.296703 | 0.622167 | 0.389999 | 0.133185 | -0.651432 | 0.098311 | -0.612388 | -0.477757 | -1.049531 | -1.558886 | 0.199438 | -0.772957 | 1.204000 | 0.094183 | -0.318508 | -0.357454 | -0.112793 | 0.685842 | -0.469426 | -0.769896 | -0.187049 | -0.232898 | -0.345233 | 0 | -0.864737 |
| 3289 | 1.250249 | 0.019063 | -1.326108 | -0.039059 | 2.232341 | 3.300602 | -0.326435 | 0.757703 | -0.156352 | 0.062703 | -0.161649 | 0.029727 | -0.018457 | 0.530951 | 1.107512 | 0.377201 | -0.926363 | 0.295044 | -0.006783 | 0.033750 | -0.009900 | -0.189322 | -0.157734 | 1.005326 | 0.838403 | -0.315582 | 0.011439 | 0.018031 | -0.233287 | 0 | -2.406930 |
| 279921 | -4.814708 | 4.736862 | -4.817819 | -1.103622 | -2.256585 | -2.425710 | -1.657050 | 3.493293 | -0.207819 | 0.013773 | -2.260313 | 0.744399 | -0.973800 | 3.250789 | -0.282599 | 0.313408 | 1.121537 | -0.022531 | -0.416665 | -0.117994 | 0.375361 | 0.554691 | 0.349764 | 0.026127 | 0.275542 | 0.148178 | 0.102320 | 0.185414 | -0.319965 | 0 | 1.362876 |
| 178297 | 2.100716 | -0.778343 | -0.596761 | -0.557506 | -0.575207 | 0.293849 | -0.958246 | 0.146132 | -0.136921 | 0.798909 | 0.428648 | 0.958404 | 0.715275 | -0.043584 | -0.140031 | -1.084006 | -0.649764 | 1.591873 | -0.423356 | -0.580698 | -0.562834 | -1.044407 | 0.459820 | 0.203965 | -0.508869 | -0.686475 | 0.053956 | -0.034934 | -0.353189 | 0 | -0.693382 |
| 224944 | 2.053311 | 0.089735 | -1.681836 | 0.454212 | 0.298310 | -0.953526 | 0.152003 | -0.207071 | 0.587335 | -0.362047 | -0.589598 | -0.174712 | -0.621127 | -0.703513 | 0.271957 | 0.318688 | 0.549365 | -0.257786 | 0.016256 | -0.187421 | -0.361158 | -0.984262 | 0.354198 | 0.620709 | -0.297138 | 0.166736 | -0.068299 | -0.029585 | -0.317287 | 0 | 0.334747 |
| 144794 | 1.963377 | 0.175655 | -1.791505 | 1.180371 | 0.493289 | -1.157260 | 0.678691 | -0.322212 | -0.273120 | 0.553350 | 0.900665 | 0.380835 | -1.197776 | 1.219675 | -0.368170 | -0.251083 | -0.545004 | 0.080937 | -0.199778 | -0.296184 | 0.188454 | 0.525823 | -0.019335 | -0.007700 | 0.374702 | -0.503352 | -0.043733 | -0.070953 | -0.233887 | 0 | -2.406930 |
| 56561 | 1.180264 | 0.668819 | -0.242382 | 1.284748 | 0.029324 | -1.039543 | 0.202761 | -0.102430 | -0.340626 | -0.508367 | 1.978050 | 0.556068 | -0.337921 | -1.095969 | 0.391429 | 0.740869 | 0.726637 | 1.040940 | -0.411526 | -0.103660 | -0.004479 | 0.014954 | -0.108992 | 0.397877 | 0.628531 | -0.356931 | 0.030663 | 0.049046 | -0.349231 | 0 | -0.179318 |
| 37115 | -2.091027 | 1.249032 | 0.841086 | -0.777488 | -0.176500 | -0.077257 | -0.118603 | -0.256751 | 0.178740 | -0.000305 | 0.991856 | 0.698911 | -0.901970 | 0.341906 | -0.643972 | -0.011763 | -0.069715 | -0.449297 | -0.255400 | -0.517288 | 0.631502 | -0.413265 | 0.293367 | -0.000012 | -0.318688 | 0.224045 | -0.725597 | -0.392266 | -0.349231 | 0 | -0.693382 |
| 58951 | 1.162447 | 0.272458 | 0.615165 | 1.058086 | -0.262004 | -0.359390 | -0.012728 | -0.015620 | 0.066470 | -0.087054 | -0.061459 | 0.470350 | 0.215349 | 0.293257 | 1.308914 | -0.006260 | -0.233542 | -0.816695 | -0.644417 | -0.141656 | -0.243925 | -0.693725 | 0.168349 | 0.031270 | 0.216868 | -0.665192 | 0.045823 | 0.031301 | -0.305252 | 0 | -0.179318 |
# 下面查看匿名属性的分布
# 匿名属性的峰度与偏度
numerical_columns = data.columns.drop(['Class','Hour','Amount'])
for num_col in numerical_columns:print('{:10}'.format(num_col), 'Skewness:', '{:8.2f}'.format(data[num_col].skew()), ' Kurtosis:', '{:8.2f}'.format(data[num_col].kurt()))
V1 Skewness: -3.28 Kurtosis: 32.49
V2 Skewness: -4.62 Kurtosis: 95.77
V3 Skewness: -2.24 Kurtosis: 26.62
V4 Skewness: 0.68 Kurtosis: 2.64
V5 Skewness: -2.43 Kurtosis: 206.90
V6 Skewness: 1.83 Kurtosis: 42.64
V7 Skewness: 2.55 Kurtosis: 405.61
V8 Skewness: -8.52 Kurtosis: 220.59
V9 Skewness: 0.55 Kurtosis: 3.73
V10 Skewness: 1.19 Kurtosis: 31.99
V11 Skewness: 0.36 Kurtosis: 1.63
V12 Skewness: -2.28 Kurtosis: 20.24
V13 Skewness: 0.07 Kurtosis: 0.20
V14 Skewness: -2.00 Kurtosis: 23.88
V15 Skewness: -0.31 Kurtosis: 0.28
V16 Skewness: -1.10 Kurtosis: 10.42
V17 Skewness: -3.84 Kurtosis: 94.80
V18 Skewness: -0.26 Kurtosis: 2.58
V19 Skewness: 0.11 Kurtosis: 1.72
V20 Skewness: -2.04 Kurtosis: 271.02
V21 Skewness: 3.59 Kurtosis: 207.29
V22 Skewness: -0.21 Kurtosis: 2.83
V23 Skewness: -5.88 Kurtosis: 440.09
V24 Skewness: -0.55 Kurtosis: 0.62
V25 Skewness: -0.42 Kurtosis: 4.29
V26 Skewness: 0.58 Kurtosis: 0.92
V27 Skewness: -1.17 Kurtosis: 244.99
V28 Skewness: 11.19 Kurtosis: 933.40
f = pd.melt(data, value_vars=numerical_columns)
g = sns.FacetGrid(f, col='variable', col_wrap=4, sharex=False, sharey=False)
g = g.map(sns.distplot, 'value')
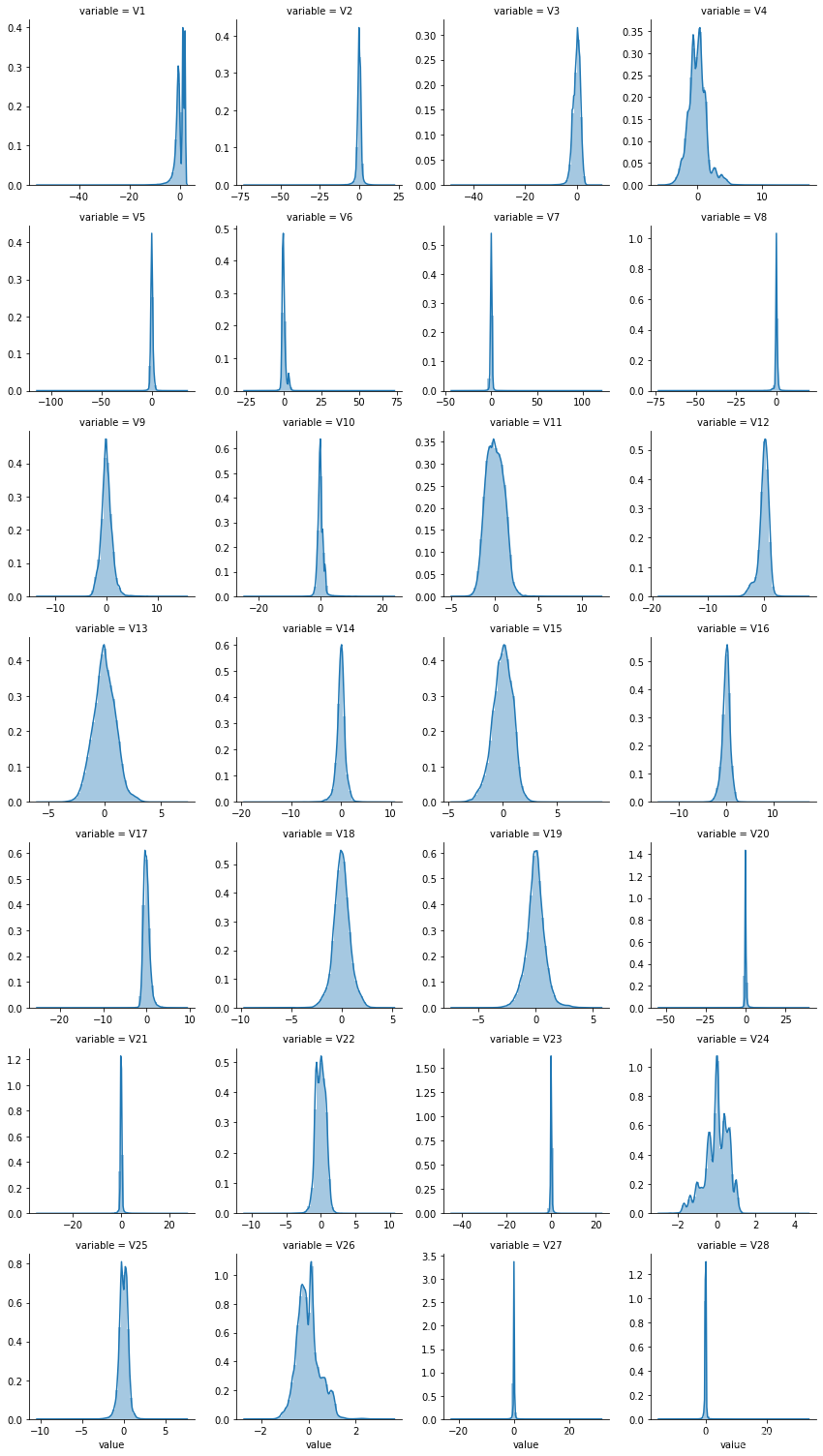
因为数据经过了标准化处理,所以匿名特征的偏度相对较小,峰度较大,分布上v_5, v_7, v_8, v_20, v_21, v_23, v_27,v_28的峰度值较高,说明这些特征的分布十分集中,其他的特征分布相对均匀。
* 分析两个属性之间的关系
# 相关性分析
plt.figure(figsize=(8, 6))
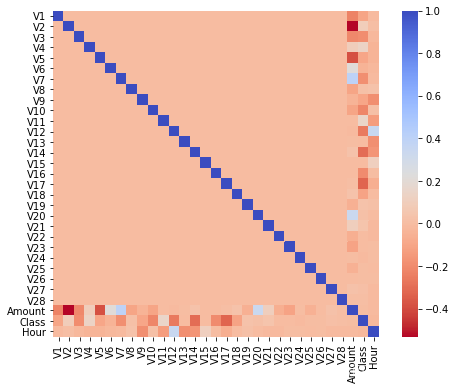
sns.heatmap(data.corr(), square=True,cmap='coolwarm_r', annot_kws={'size': 20})
plt.show()
data.corr()
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 | V17 | V18 | V19 | V20 | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Amount | Class | Hour | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V1 | 1.000000e+00 | 1.717515e-16 | -9.049057e-16 | -2.483769e-16 | 3.029761e-16 | 1.242968e-16 | 4.904952e-17 | -2.809306e-17 | 5.255584e-17 | 5.521194e-17 | 2.590354e-16 | 1.898607e-16 | -3.778206e-17 | 4.132544e-16 | -1.522953e-16 | 3.007488e-16 | -3.106689e-17 | 1.645281e-16 | 1.045442e-16 | 9.852066e-17 | -1.808291e-16 | 7.990046e-17 | 1.056762e-16 | -5.113541e-17 | -2.165870e-16 | -1.408070e-16 | 1.664818e-16 | 2.419798e-16 | -0.227709 | -0.101347 | -0.005214 |
| V2 | 1.717515e-16 | 1.000000e+00 | 9.206734e-17 | -1.226183e-16 | 1.487342e-16 | 3.492970e-16 | -4.501183e-17 | -5.839820e-17 | -1.832049e-16 | -2.598347e-16 | 3.312314e-16 | -3.228806e-16 | -1.091369e-16 | -4.657267e-16 | 5.392819e-17 | -3.749559e-18 | -5.591430e-16 | 2.877862e-16 | -1.672445e-17 | 3.898167e-17 | 4.667231e-17 | 1.203109e-16 | 3.242403e-16 | -1.254911e-16 | 8.784216e-17 | 2.450901e-16 | -5.467509e-16 | -6.910935e-17 | -0.531409 | 0.091289 | 0.007802 |
| V3 | -9.049057e-16 | 9.206734e-17 | 1.000000e+00 | -2.981464e-16 | -6.943096e-16 | 1.308147e-15 | 2.120327e-16 | -8.586741e-17 | 9.780262e-17 | 2.764966e-16 | 1.500352e-16 | 2.182812e-16 | -4.679364e-17 | 6.942636e-16 | -5.333200e-17 | 5.460118e-16 | 2.134100e-16 | 2.870116e-16 | 3.728807e-16 | 1.267443e-16 | 1.189711e-16 | -2.343257e-16 | -8.182206e-17 | -3.300147e-17 | 1.123060e-16 | -2.136494e-16 | 4.752587e-16 | 6.073110e-16 | -0.210880 | -0.192961 | -0.021569 |
| V4 | -2.483769e-16 | -1.226183e-16 | -2.981464e-16 | 1.000000e+00 | -1.903391e-15 | -4.169652e-16 | -6.535390e-17 | 5.942856e-16 | 6.175719e-16 | -6.910284e-17 | -2.936726e-16 | -1.448546e-16 | 3.050372e-17 | -8.547776e-17 | 2.459280e-16 | -8.218577e-17 | -4.443050e-16 | 5.369916e-18 | -2.842719e-16 | -2.222520e-16 | 1.390687e-17 | 2.189964e-16 | 1.663593e-16 | 1.403733e-16 | 6.312530e-16 | -4.009636e-16 | -6.309346e-17 | -2.064064e-16 | 0.098732 | 0.133447 | -0.035063 |
| V5 | 3.029761e-16 | 1.487342e-16 | -6.943096e-16 | -1.903391e-15 | 1.000000e+00 | 1.159613e-15 | 7.659742e-17 | 7.328495e-16 | 4.435269e-16 | 1.632311e-16 | 6.784587e-16 | 4.520778e-16 | -2.979964e-16 | 2.516209e-16 | 1.016075e-16 | 6.264287e-16 | 4.535815e-16 | 4.196874e-16 | -1.277261e-16 | -2.414281e-16 | 9.325965e-17 | -6.982655e-17 | -1.848644e-16 | -9.892370e-16 | -1.561416e-16 | 3.403172e-16 | 3.299056e-16 | -3.491468e-16 | -0.386356 | -0.094974 | -0.035134 |
| V6 | 1.242968e-16 | 3.492970e-16 | 1.308147e-15 | -4.169652e-16 | 1.159613e-15 | 1.000000e+00 | -2.949670e-16 | -3.474079e-16 | -1.008735e-16 | 1.322142e-16 | 8.380230e-16 | 2.570184e-16 | -1.251524e-16 | 3.531769e-16 | -6.825844e-17 | -1.823748e-16 | 1.161080e-16 | 6.313161e-17 | 6.136340e-17 | -1.318056e-16 | -4.925144e-17 | -9.729827e-17 | -3.176032e-17 | -1.125379e-15 | 5.563670e-16 | -2.627057e-16 | -4.040640e-16 | 4.612882e-17 | 0.215981 | -0.043643 | -0.018945 |
| V7 | 4.904952e-17 | -4.501183e-17 | 2.120327e-16 | -6.535390e-17 | 7.659742e-17 | -2.949670e-16 | 1.000000e+00 | 3.038794e-17 | -5.250969e-17 | 3.186953e-16 | -3.362622e-16 | 7.265464e-16 | -1.485108e-16 | 7.720708e-17 | -1.845909e-16 | 4.901078e-16 | 7.173458e-16 | 1.638629e-16 | -1.132423e-16 | 1.889527e-16 | -7.597231e-17 | -6.887963e-16 | 1.393022e-16 | 2.078026e-17 | -1.507689e-17 | -7.709408e-16 | -2.647380e-18 | 2.115388e-17 | 0.397311 | -0.187257 | -0.009729 |
| V8 | -2.809306e-17 | -5.839820e-17 | -8.586741e-17 | 5.942856e-16 | 7.328495e-16 | -3.474079e-16 | 3.038794e-17 | 1.000000e+00 | 4.683000e-16 | -3.022868e-16 | 1.499830e-16 | 3.887009e-17 | -3.213252e-16 | -2.288651e-16 | 1.109628e-16 | 2.500367e-16 | -3.808536e-16 | -3.119192e-16 | -3.559019e-16 | 1.098800e-17 | -2.338214e-16 | -6.701600e-18 | 2.701514e-16 | -2.444390e-16 | -1.792313e-16 | 1.092765e-17 | 3.921512e-16 | -5.158971e-16 | -0.103079 | 0.019875 | 0.032106 |
| V9 | 5.255584e-17 | -1.832049e-16 | 9.780262e-17 | 6.175719e-16 | 4.435269e-16 | -1.008735e-16 | -5.250969e-17 | 4.683000e-16 | 1.000000e+00 | -4.733827e-16 | 3.289603e-16 | -1.339732e-15 | 9.374886e-16 | 9.287436e-16 | -8.883532e-16 | -5.409347e-16 | 7.071023e-16 | 1.471108e-16 | 1.293082e-16 | -3.112119e-16 | 2.755460e-16 | -2.171404e-16 | -1.011218e-16 | -2.940457e-16 | 2.137255e-16 | -1.039639e-16 | -1.499396e-16 | 7.982292e-16 | -0.044246 | -0.097733 | -0.189830 |
| V10 | 5.521194e-17 | -2.598347e-16 | 2.764966e-16 | -6.910284e-17 | 1.632311e-16 | 1.322142e-16 | 3.186953e-16 | -3.022868e-16 | -4.733827e-16 | 1.000000e+00 | -3.633385e-16 | 8.563304e-16 | -4.013607e-16 | 6.638602e-16 | 3.932439e-16 | 1.882434e-16 | 6.617837e-16 | 4.829483e-16 | 4.623218e-17 | -1.340974e-15 | 1.048675e-15 | -2.890990e-16 | 1.907376e-16 | -7.312196e-17 | -3.457860e-16 | -4.117783e-16 | -3.115507e-16 | 3.949646e-16 | -0.101502 | -0.216883 | 0.024177 |
| V11 | 2.590354e-16 | 3.312314e-16 | 1.500352e-16 | -2.936726e-16 | 6.784587e-16 | 8.380230e-16 | -3.362622e-16 | 1.499830e-16 | 3.289603e-16 | -3.633385e-16 | 1.000000e+00 | -7.116039e-16 | 4.369928e-16 | -1.283496e-16 | 1.903820e-16 | 1.158881e-16 | 6.624541e-16 | 9.910529e-17 | -1.093636e-15 | -1.478641e-16 | 6.632474e-18 | 1.312323e-17 | 1.404725e-16 | 1.672342e-15 | -6.082687e-16 | -1.240097e-16 | -1.519253e-16 | -2.909057e-16 | 0.000104 | 0.154876 | -0.135131 |
| V12 | 1.898607e-16 | -3.228806e-16 | 2.182812e-16 | -1.448546e-16 | 4.520778e-16 | 2.570184e-16 | 7.265464e-16 | 3.887009e-17 | -1.339732e-15 | 8.563304e-16 | -7.116039e-16 | 1.000000e+00 | -2.297323e-14 | 4.486162e-16 | -3.033543e-16 | 4.714076e-16 | -3.797286e-16 | -6.830564e-16 | 1.782434e-16 | 2.673446e-16 | 5.724276e-16 | -3.587155e-17 | 3.029886e-16 | 4.510178e-16 | 6.970336e-18 | 1.653468e-16 | -2.721798e-16 | 7.065902e-16 | -0.009542 | -0.260593 | 0.352459 |
| V13 | -3.778206e-17 | -1.091369e-16 | -4.679364e-17 | 3.050372e-17 | -2.979964e-16 | -1.251524e-16 | -1.485108e-16 | -3.213252e-16 | 9.374886e-16 | -4.013607e-16 | 4.369928e-16 | -2.297323e-14 | 1.000000e+00 | 1.415589e-15 | -1.185819e-16 | 4.849394e-16 | 8.705885e-17 | 2.432753e-16 | -6.331767e-17 | -3.200986e-17 | 1.428638e-16 | -4.602453e-17 | -7.174408e-16 | -6.376621e-16 | -1.142909e-16 | -1.478991e-16 | -5.300185e-16 | 1.043260e-15 | 0.005293 | -0.004570 | -0.187981 |
| V14 | 4.132544e-16 | -4.657267e-16 | 6.942636e-16 | -8.547776e-17 | 2.516209e-16 | 3.531769e-16 | 7.720708e-17 | -2.288651e-16 | 9.287436e-16 | 6.638602e-16 | -1.283496e-16 | 4.486162e-16 | 1.415589e-15 | 1.000000e+00 | -2.864454e-16 | -8.191302e-16 | 1.131442e-15 | -3.009169e-16 | 2.138702e-16 | -5.239826e-17 | -2.462983e-16 | 6.492362e-16 | 2.160339e-16 | -1.258007e-17 | -7.178656e-17 | -2.488490e-17 | -1.739150e-17 | 2.414117e-15 | 0.033751 | -0.302544 | -0.162918 |
| V15 | -1.522953e-16 | 5.392819e-17 | -5.333200e-17 | 2.459280e-16 | 1.016075e-16 | -6.825844e-17 | -1.845909e-16 | 1.109628e-16 | -8.883532e-16 | 3.932439e-16 | 1.903820e-16 | -3.033543e-16 | -1.185819e-16 | -2.864454e-16 | 1.000000e+00 | 9.678376e-16 | -5.606434e-16 | 6.692616e-16 | -1.423455e-15 | 2.118638e-16 | 6.349939e-17 | -3.516820e-16 | 1.024768e-16 | -4.337014e-16 | 2.281677e-16 | 1.108681e-16 | -1.246909e-15 | -9.799748e-16 | -0.002986 | -0.004223 | 0.112251 |
| V16 | 3.007488e-16 | -3.749559e-18 | 5.460118e-16 | -8.218577e-17 | 6.264287e-16 | -1.823748e-16 | 4.901078e-16 | 2.500367e-16 | -5.409347e-16 | 1.882434e-16 | 1.158881e-16 | 4.714076e-16 | 4.849394e-16 | -8.191302e-16 | 9.678376e-16 | 1.000000e+00 | 1.641102e-15 | -2.666175e-15 | 1.138371e-15 | 4.407936e-16 | -4.180114e-16 | 2.653008e-16 | 7.410993e-16 | -3.508969e-16 | -3.341605e-16 | -4.690618e-16 | 8.147869e-16 | 7.042089e-16 | -0.003910 | -0.196539 | 0.005517 |
| V17 | -3.106689e-17 | -5.591430e-16 | 2.134100e-16 | -4.443050e-16 | 4.535815e-16 | 1.161080e-16 | 7.173458e-16 | -3.808536e-16 | 7.071023e-16 | 6.617837e-16 | 6.624541e-16 | -3.797286e-16 | 8.705885e-17 | 1.131442e-15 | -5.606434e-16 | 1.641102e-15 | 1.000000e+00 | -5.251666e-15 | 3.694474e-16 | -8.921672e-16 | -1.086035e-15 | -3.486998e-16 | 4.072307e-16 | -1.897694e-16 | 7.587211e-17 | 2.084478e-16 | 6.669179e-16 | -5.419071e-17 | 0.007309 | -0.326481 | -0.064803 |
| V18 | 1.645281e-16 | 2.877862e-16 | 2.870116e-16 | 5.369916e-18 | 4.196874e-16 | 6.313161e-17 | 1.638629e-16 | -3.119192e-16 | 1.471108e-16 | 4.829483e-16 | 9.910529e-17 | -6.830564e-16 | 2.432753e-16 | -3.009169e-16 | 6.692616e-16 | -2.666175e-15 | -5.251666e-15 | 1.000000e+00 | -2.719935e-15 | -4.098224e-16 | -1.240266e-15 | -5.279657e-16 | -2.362311e-16 | -1.869482e-16 | -2.451121e-16 | 3.089442e-16 | 2.209663e-16 | 8.158517e-16 | 0.035650 | -0.111485 | -0.003518 |
| V19 | 1.045442e-16 | -1.672445e-17 | 3.728807e-16 | -2.842719e-16 | -1.277261e-16 | 6.136340e-17 | -1.132423e-16 | -3.559019e-16 | 1.293082e-16 | 4.623218e-17 | -1.093636e-15 | 1.782434e-16 | -6.331767e-17 | 2.138702e-16 | -1.423455e-15 | 1.138371e-15 | 3.694474e-16 | -2.719935e-15 | 1.000000e+00 | 2.693620e-16 | 6.052450e-16 | -1.036140e-15 | 5.861740e-16 | -9.630049e-17 | 8.161694e-16 | 5.479257e-16 | -1.243578e-16 | -1.291833e-15 | -0.056151 | 0.034783 | 0.021566 |
| V20 | 9.852066e-17 | 3.898167e-17 | 1.267443e-16 | -2.222520e-16 | -2.414281e-16 | -1.318056e-16 | 1.889527e-16 | 1.098800e-17 | -3.112119e-16 | -1.340974e-15 | -1.478641e-16 | 2.673446e-16 | -3.200986e-17 | -5.239826e-17 | 2.118638e-16 | 4.407936e-16 | -8.921672e-16 | -4.098224e-16 | 2.693620e-16 | 1.000000e+00 | -1.118296e-15 | 1.101689e-15 | 1.107203e-16 | 1.749671e-16 | -6.786605e-18 | -3.590893e-16 | -8.488785e-16 | -4.584320e-16 | 0.339403 | 0.020090 | 0.000978 |
| V21 | -1.808291e-16 | 4.667231e-17 | 1.189711e-16 | 1.390687e-17 | 9.325965e-17 | -4.925144e-17 | -7.597231e-17 | -2.338214e-16 | 2.755460e-16 | 1.048675e-15 | 6.632474e-18 | 5.724276e-16 | 1.428638e-16 | -2.462983e-16 | 6.349939e-17 | -4.180114e-16 | -1.086035e-15 | -1.240266e-15 | 6.052450e-16 | -1.118296e-15 | 1.000000e+00 | 3.540128e-15 | 4.521934e-16 | 1.014531e-16 | -1.173906e-16 | -4.337929e-16 | -1.484206e-15 | 1.584856e-16 | 0.105999 | 0.040413 | -0.011915 |
| V22 | 7.990046e-17 | 1.203109e-16 | -2.343257e-16 | 2.189964e-16 | -6.982655e-17 | -9.729827e-17 | -6.887963e-16 | -6.701600e-18 | -2.171404e-16 | -2.890990e-16 | 1.312323e-17 | -3.587155e-17 | -4.602453e-17 | 6.492362e-16 | -3.516820e-16 | 2.653008e-16 | -3.486998e-16 | -5.279657e-16 | -1.036140e-15 | 1.101689e-15 | 3.540128e-15 | 1.000000e+00 | 3.086083e-16 | 6.736130e-17 | -9.827185e-16 | -2.194486e-17 | 1.478149e-16 | -5.686304e-16 | -0.064801 | 0.000805 | -0.016610 |
| V23 | 1.056762e-16 | 3.242403e-16 | -8.182206e-17 | 1.663593e-16 | -1.848644e-16 | -3.176032e-17 | 1.393022e-16 | 2.701514e-16 | -1.011218e-16 | 1.907376e-16 | 1.404725e-16 | 3.029886e-16 | -7.174408e-16 | 2.160339e-16 | 1.024768e-16 | 7.410993e-16 | 4.072307e-16 | -2.362311e-16 | 5.861740e-16 | 1.107203e-16 | 4.521934e-16 | 3.086083e-16 | 1.000000e+00 | 7.328447e-17 | -7.508801e-16 | 1.284451e-15 | 4.254579e-16 | 1.281294e-15 | -0.112633 | -0.002685 | 0.006004 |
| V24 | -5.113541e-17 | -1.254911e-16 | -3.300147e-17 | 1.403733e-16 | -9.892370e-16 | -1.125379e-15 | 2.078026e-17 | -2.444390e-16 | -2.940457e-16 | -7.312196e-17 | 1.672342e-15 | 4.510178e-16 | -6.376621e-16 | -1.258007e-17 | -4.337014e-16 | -3.508969e-16 | -1.897694e-16 | -1.869482e-16 | -9.630049e-17 | 1.749671e-16 | 1.014531e-16 | 6.736130e-17 | 7.328447e-17 | 1.000000e+00 | 1.242718e-15 | 1.863258e-16 | -2.894257e-16 | -2.844233e-16 | 0.005146 | -0.007221 | 0.004328 |
| V25 | -2.165870e-16 | 8.784216e-17 | 1.123060e-16 | 6.312530e-16 | -1.561416e-16 | 5.563670e-16 | -1.507689e-17 | -1.792313e-16 | 2.137255e-16 | -3.457860e-16 | -6.082687e-16 | 6.970336e-18 | -1.142909e-16 | -7.178656e-17 | 2.281677e-16 | -3.341605e-16 | 7.587211e-17 | -2.451121e-16 | 8.161694e-16 | -6.786605e-18 | -1.173906e-16 | -9.827185e-16 | -7.508801e-16 | 1.242718e-15 | 1.000000e+00 | 2.449277e-15 | -5.340203e-16 | 2.699748e-16 | -0.047837 | 0.003308 | -0.003497 |
| V26 | -1.408070e-16 | 2.450901e-16 | -2.136494e-16 | -4.009636e-16 | 3.403172e-16 | -2.627057e-16 | -7.709408e-16 | 1.092765e-17 | -1.039639e-16 | -4.117783e-16 | -1.240097e-16 | 1.653468e-16 | -1.478991e-16 | -2.488490e-17 | 1.108681e-16 | -4.690618e-16 | 2.084478e-16 | 3.089442e-16 | 5.479257e-16 | -3.590893e-16 | -4.337929e-16 | -2.194486e-17 | 1.284451e-15 | 1.863258e-16 | 2.449277e-15 | 1.000000e+00 | -2.939564e-16 | -2.558739e-16 | -0.003208 | 0.004455 | 0.001146 |
| V27 | 1.664818e-16 | -5.467509e-16 | 4.752587e-16 | -6.309346e-17 | 3.299056e-16 | -4.040640e-16 | -2.647380e-18 | 3.921512e-16 | -1.499396e-16 | -3.115507e-16 | -1.519253e-16 | -2.721798e-16 | -5.300185e-16 | -1.739150e-17 | -1.246909e-15 | 8.147869e-16 | 6.669179e-16 | 2.209663e-16 | -1.243578e-16 | -8.488785e-16 | -1.484206e-15 | 1.478149e-16 | 4.254579e-16 | -2.894257e-16 | -5.340203e-16 | -2.939564e-16 | 1.000000e+00 | -2.403217e-16 | 0.028825 | 0.017580 | -0.008676 |
| V28 | 2.419798e-16 | -6.910935e-17 | 6.073110e-16 | -2.064064e-16 | -3.491468e-16 | 4.612882e-17 | 2.115388e-17 | -5.158971e-16 | 7.982292e-16 | 3.949646e-16 | -2.909057e-16 | 7.065902e-16 | 1.043260e-15 | 2.414117e-15 | -9.799748e-16 | 7.042089e-16 | -5.419071e-17 | 8.158517e-16 | -1.291833e-15 | -4.584320e-16 | 1.584856e-16 | -5.686304e-16 | 1.281294e-15 | -2.844233e-16 | 2.699748e-16 | -2.558739e-16 | -2.403217e-16 | 1.000000e+00 | 0.010258 | 0.009536 | -0.007492 |
| Amount | -2.277087e-01 | -5.314089e-01 | -2.108805e-01 | 9.873167e-02 | -3.863563e-01 | 2.159812e-01 | 3.973113e-01 | -1.030791e-01 | -4.424560e-02 | -1.015021e-01 | 1.039770e-04 | -9.541802e-03 | 5.293409e-03 | 3.375117e-02 | -2.985848e-03 | -3.909527e-03 | 7.309042e-03 | 3.565034e-02 | -5.615079e-02 | 3.394034e-01 | 1.059989e-01 | -6.480065e-02 | -1.126326e-01 | 5.146217e-03 | -4.783686e-02 | -3.208037e-03 | 2.882546e-02 | 1.025822e-02 | 1.000000 | 0.005632 | -0.006667 |
| Class | -1.013473e-01 | 9.128865e-02 | -1.929608e-01 | 1.334475e-01 | -9.497430e-02 | -4.364316e-02 | -1.872566e-01 | 1.987512e-02 | -9.773269e-02 | -2.168829e-01 | 1.548756e-01 | -2.605929e-01 | -4.569779e-03 | -3.025437e-01 | -4.223402e-03 | -1.965389e-01 | -3.264811e-01 | -1.114853e-01 | 3.478301e-02 | 2.009032e-02 | 4.041338e-02 | 8.053175e-04 | -2.685156e-03 | -7.220907e-03 | 3.307706e-03 | 4.455398e-03 | 1.757973e-02 | 9.536041e-03 | 0.005632 | 1.000000 | -0.017109 |
| Hour | -5.214205e-03 | 7.802199e-03 | -2.156874e-02 | -3.506295e-02 | -3.513442e-02 | -1.894502e-02 | -9.729167e-03 | 3.210647e-02 | -1.898298e-01 | 2.417660e-02 | -1.351310e-01 | 3.524592e-01 | -1.879810e-01 | -1.629179e-01 | 1.122505e-01 | 5.517040e-03 | -6.480333e-02 | -3.518403e-03 | 2.156599e-02 | 9.780928e-04 | -1.191466e-02 | -1.660982e-02 | 6.004232e-03 | 4.328237e-03 | -3.497363e-03 | 1.146125e-03 | -8.676362e-03 | -7.492140e-03 | -0.006667 | -0.017109 | 1.000000 |
从数值上看,数值变量之间没有明显的相关性,因为样本的不均衡,数值变量与预测类别之间的相关性也不大,这并不是我们想看到的,因而我们考虑先进行正负样本的均衡
但是在进行样本均衡化处理之前,我们需要先对样本进行训练集和测试集的划分,这是为了保证测试的公平性,我们需要在原始数据集上测试,毕竟不能用自己构造的数据训练集测试自己构造的测试集
为了使得训练集和测试集的正负样本分布一致,采用StratifiedKFold来划分
from sklearn.model_selection import StratifiedKFold
X_original = data.drop(columns='Class')
y_original = data['Class']
sss = StratifiedKFold(n_splits=5,random_state=None,shuffle=False)
for train_index,test_index in sss.split(X_original,y_original):print('Train:',train_index,'test:',test_index)X_train,X_test = X_original.iloc[train_index],X_original.iloc[test_index]y_train,y_test = y_original.iloc[train_index],y_original.iloc[test_index]print(X_train.shape)
print(X_test.shape)
Train: [ 52587 52905 53232 ... 284804 284805 284806] test: [ 0 1 2 ... 56966 56967 56968]
Train: [ 0 1 2 ... 284804 284805 284806] test: [ 52587 52905 53232 ... 113937 113938 113939]
Train: [ 0 1 2 ... 284804 284805 284806] test: [104762 104905 105953 ... 170897 170898 170899]
Train: [ 0 1 2 ... 284804 284805 284806] test: [162214 162834 162995 ... 227854 227855 227856]
Train: [ 0 1 2 ... 227854 227855 227856] test: [222268 222591 222837 ... 284804 284805 284806]
(227846, 30)
(56961, 30)
#查看训练集和测试集的类别分布是否一致
print('Train:',[y_train.value_counts()/y_train.value_counts().sum()])
print('Test:',[y_test.value_counts()/y_test.value_counts().sum()])
Train: [0 0.998271
1 0.001729
Name: Class, dtype: float64]
Test: [0 0.99828
1 0.00172
Name: Class, dtype: float64]
对于处理正负样本极不均衡的情况,主要有欠采样和过采样两种方案.
- 欠采样是从大样本中随机选择与小样本同样数量的样本,对于极不均衡的问题会出现欠拟合问题,因为样本量太小。采用的方法是:
from imblearn.under_sampling import RandomUnderSamplerrus = RandomUnderSampler(random_state=1)X_undersampled,y_undersampled = rus.fit_resampled(X,y)
- 过采样是利用利用小样本生成与大样本相同数量的样本,有两种方法:随机过采样和SMOTE法过采样
- 随机过采样是从小样本中随机抽取一定的数量的旧样本,组成一个与大样本相同数量的新样本,这种处理方法容易出现过拟合
from imblearn.over_sampling import RandomOverSampler ros = RandomOverSampler(random_state = 1) X_oversampled,y_oversampled = ros.fit_resample(X,y)- SMOTE,即合成少数类过采样技术,针对随机过采样容易出现过拟合问题的改进方案。根据样本不同,分成数据多和数据少的两类,从数据少的类中随机选一个样本,再找到小类样本中离选定样本点近的几个样本,取这几个样本与选定样本连线上的点,作为新生成的样本,重复步骤直到达到大样本的样本数。
from imblearn.over_sampling import SMOTE smote = SMOTE(random_state = 1) X_smotesampled,y_smotesampled = smote.fit_resample(X,y)
可以利用Counter(y_smotesampled)查看两种样本的数量是否一致
下面分别用随机下采样和SMOTE与随机下采样的结合,这两种方案来对样本进行处理,并分析对比处理后样本的分布情况
from imblearn.under_sampling import RandomUnderSampler
from imblearn.over_sampling import RandomOverSampler
from imblearn.over_sampling import SMOTE
from collections import CounterX = X_train.copy()
y = y_train.copy()
print('Imblanced samples: ', Counter(y))rus = RandomUnderSampler(random_state=1)
X_rus, y_rus = rus.fit_resample(X, y)
print('Random under sample: ', Counter(y_rus))
ros = RandomOverSampler(random_state=1)
X_ros, y_ros = ros.fit_resample(X, y)
print('Random over sample: ', Counter(y_ros))
smote = SMOTE(random_state=1,sampling_strategy=0.5)
X_smote, y_smote = smote.fit_resample(X, y)
print('SMOTE: ', Counter(y_smote))
under = RandomUnderSampler(sampling_strategy=1)
X_smote, y_smote = under.fit_resample(X_smote,y_smote)
print('SMOTE: ', Counter(y_smote))
Imblanced samples: Counter({0: 227452, 1: 394})
Random under sample: Counter({0: 394, 1: 394})
Random over sample: Counter({0: 227452, 1: 227452})
SMOTE: Counter({0: 227452, 1: 113726})
SMOTE: Counter({0: 113726, 1: 113726})
根据结果,可以看出处理后的样本数,欠采样是正负样本都变成了394,而过采样是都变成了227452。下面分别分析不同平衡样本的情况
随机下采样 Random under sample
data_rus = pd.concat([X_rus,y_rus],axis=1)
# 单个数值特征分布情况
f = pd.melt(data_rus, value_vars=X_train.columns)
g = sns.FacetGrid(f, col='variable', col_wrap=3, sharex=False, sharey=False)
g = g.map(sns.distplot, 'value')
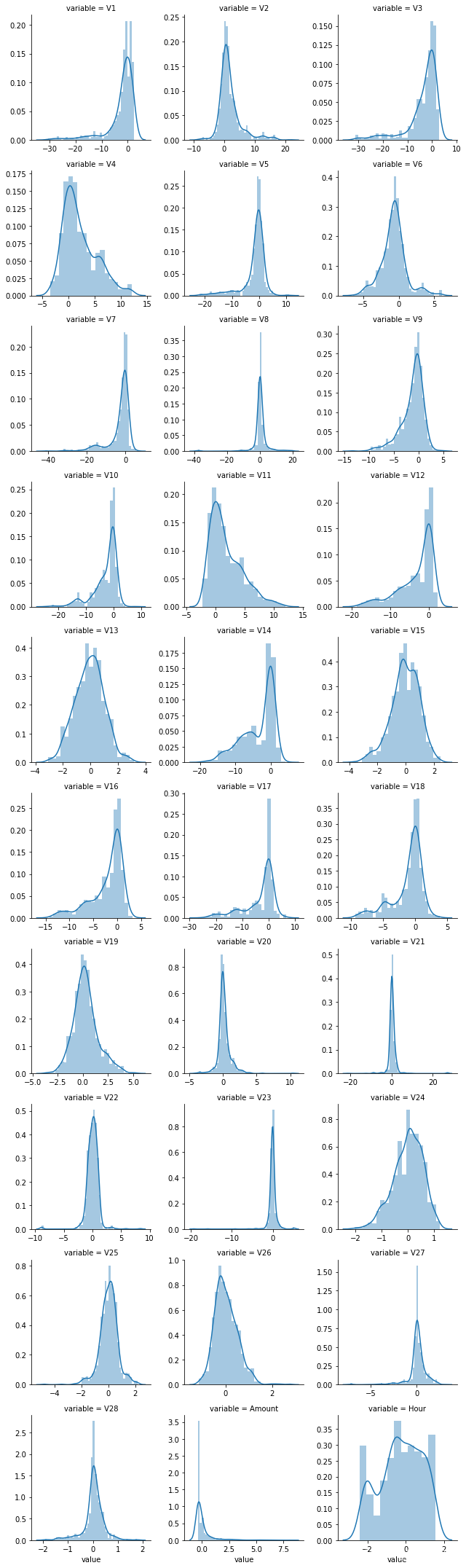
# 单个数值特征分布箱线图
f = pd.melt(data_rus, value_vars=X_train.columns)
g = sns.FacetGrid(f,col='variable', col_wrap=3, sharex=False, sharey=False,size=5)
g = g.map(sns.boxplot, 'value', color='lightskyblue')
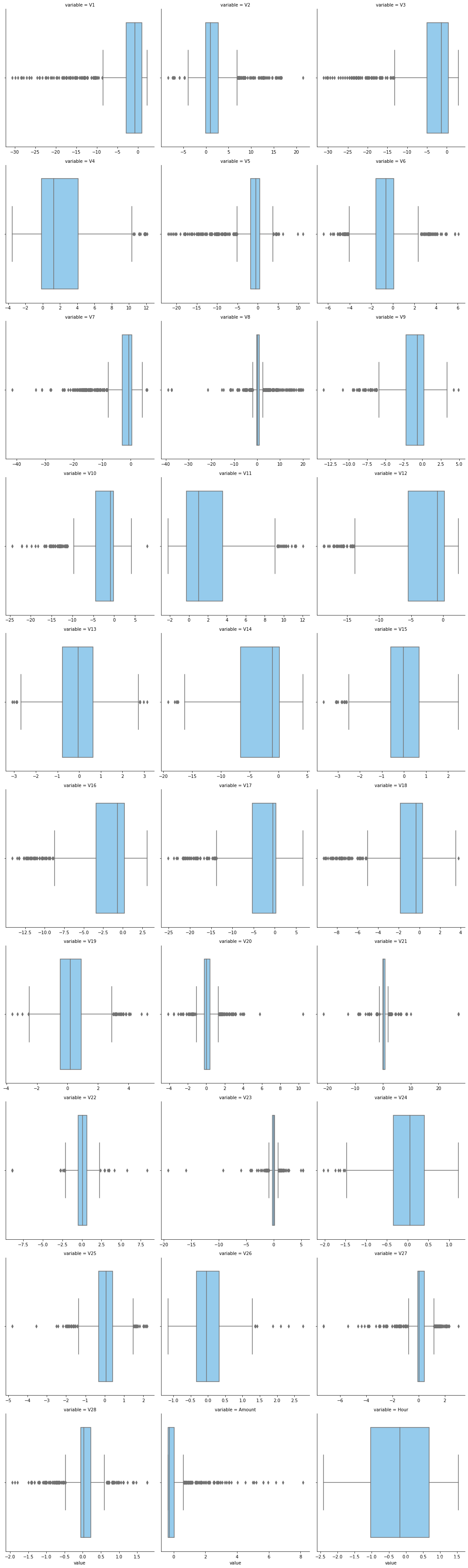
# 单个数值特征分布小提琴图
f = pd.melt(data_rus, value_vars=X_train.columns)
g = sns.FacetGrid(f, col='variable', col_wrap=3, sharex=False, sharey=False,size=5)
g = g.map(sns.violinplot, 'value',color='lightskyblue')
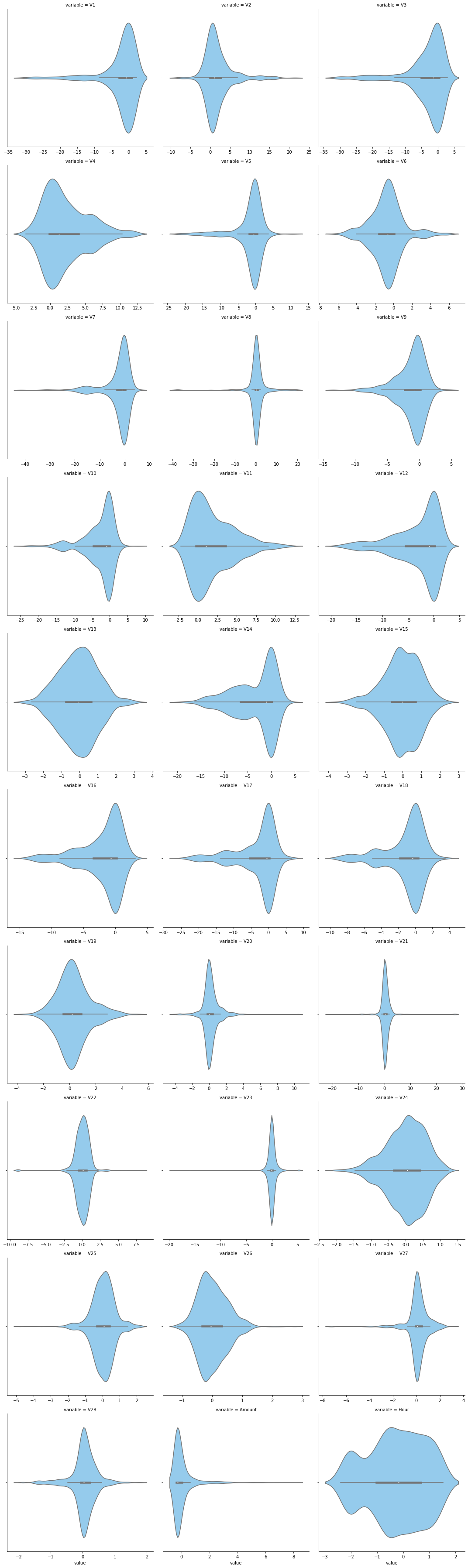
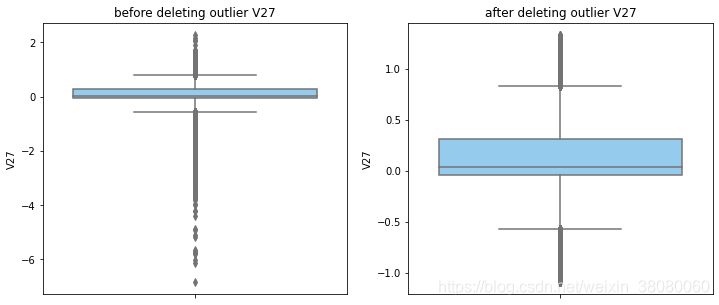
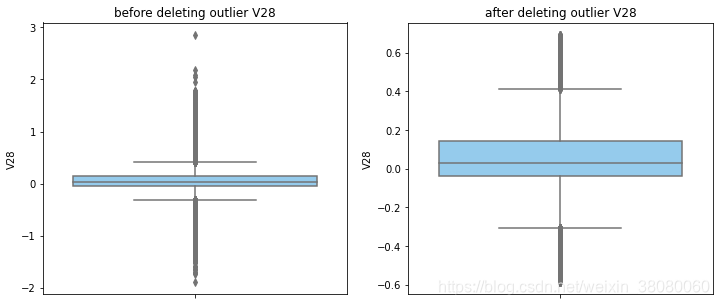
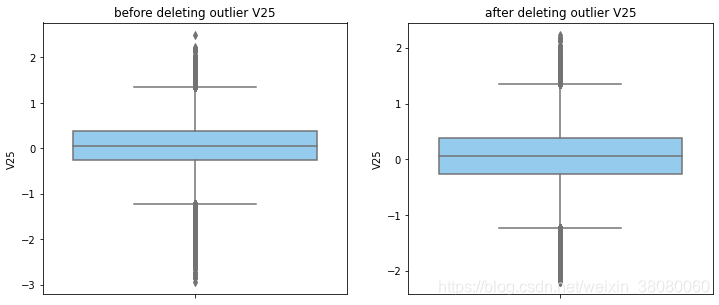
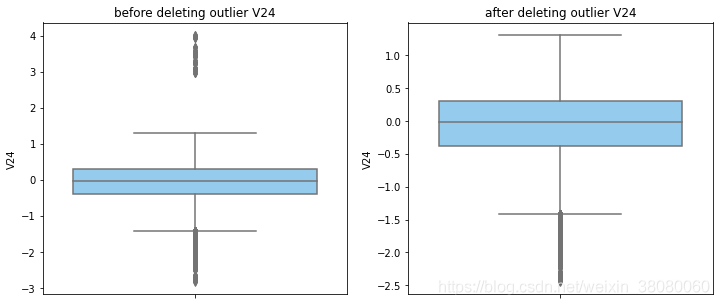
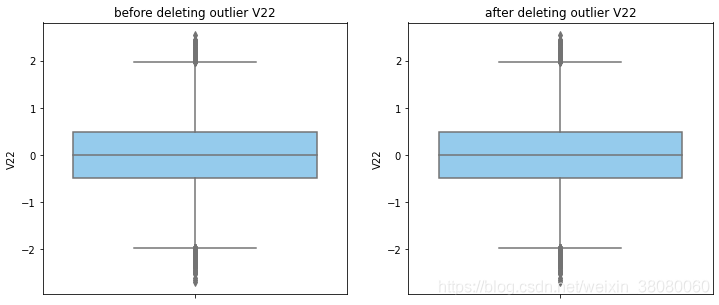
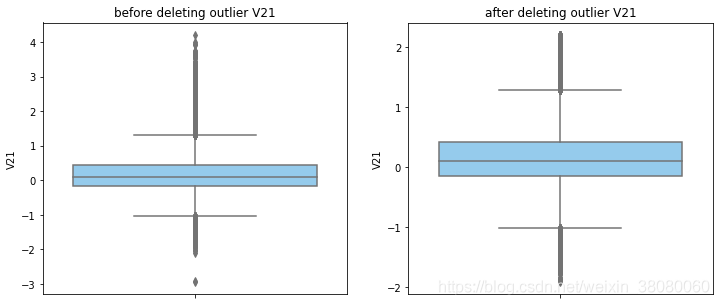
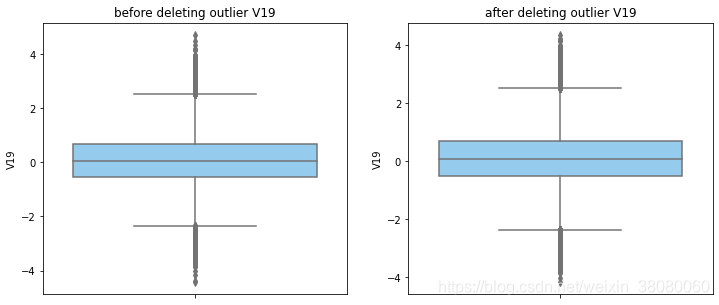
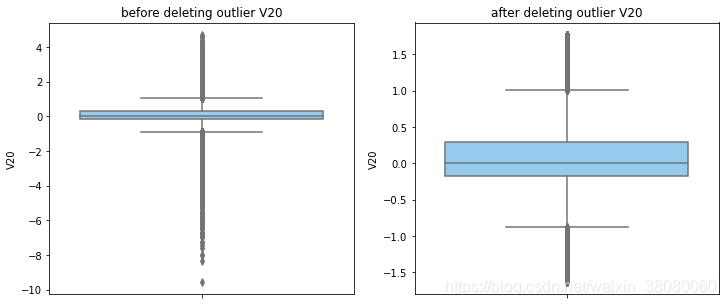
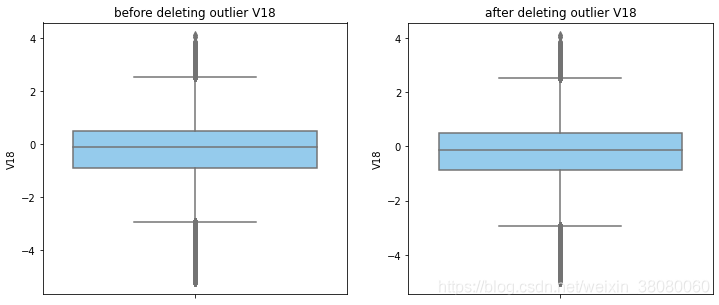
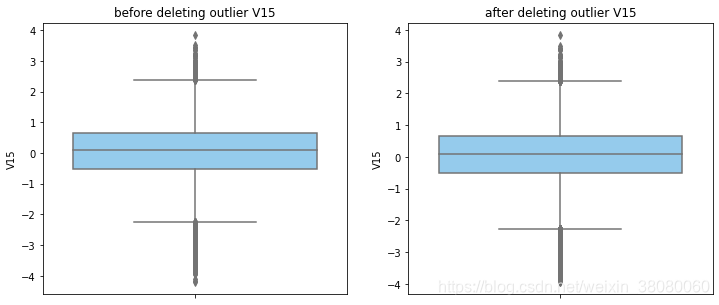
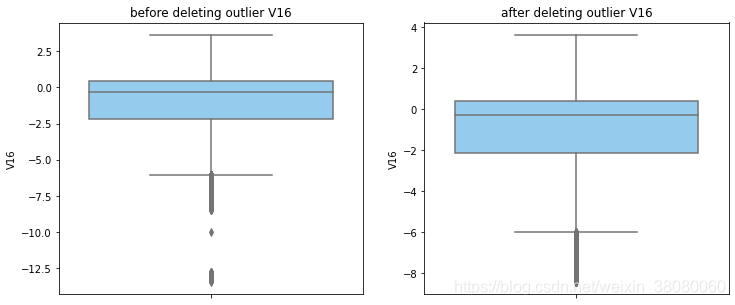
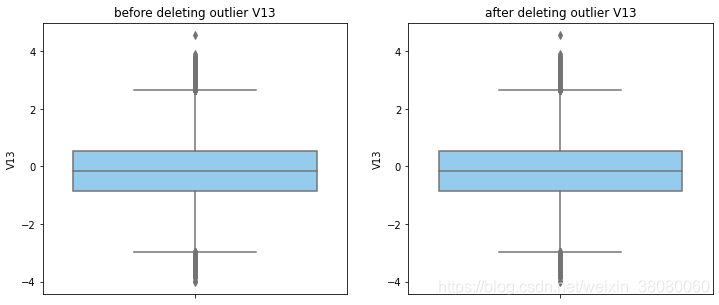
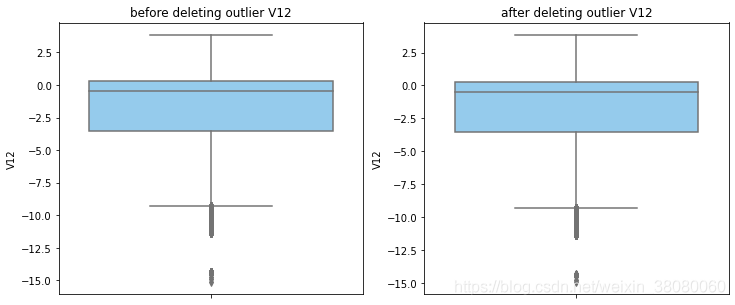
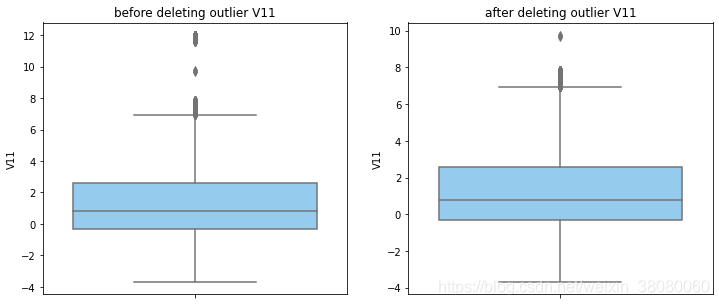
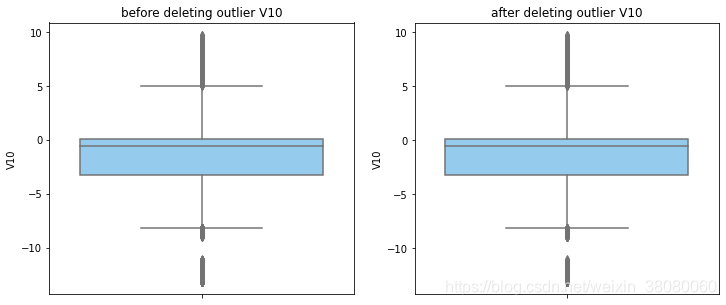
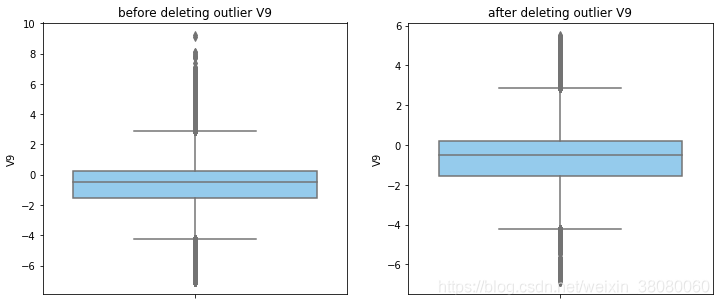
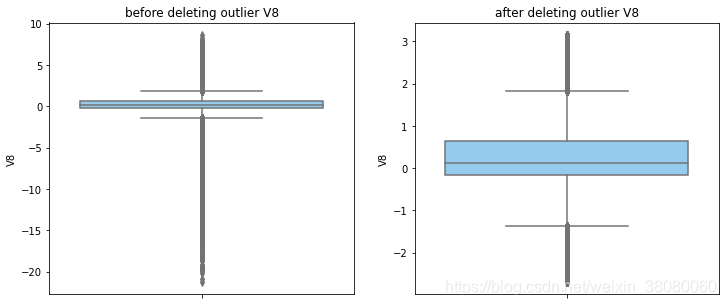
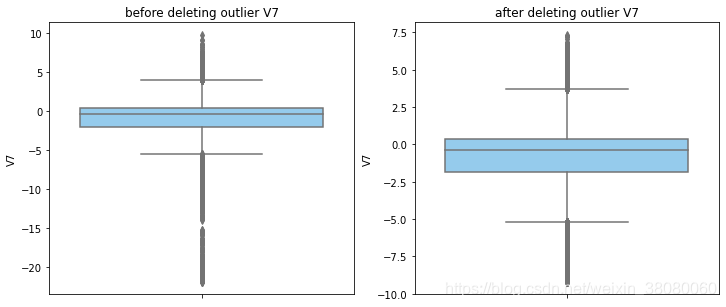
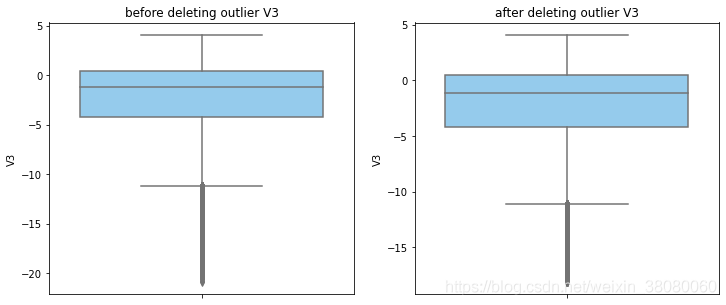
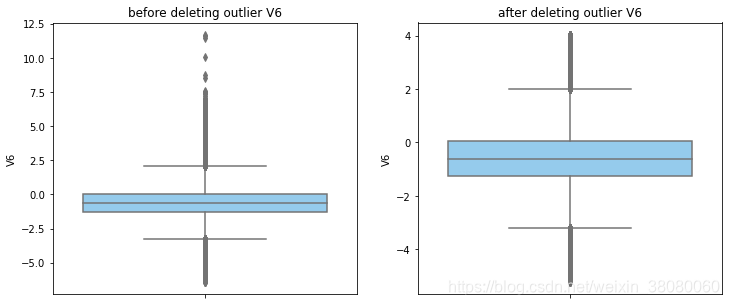
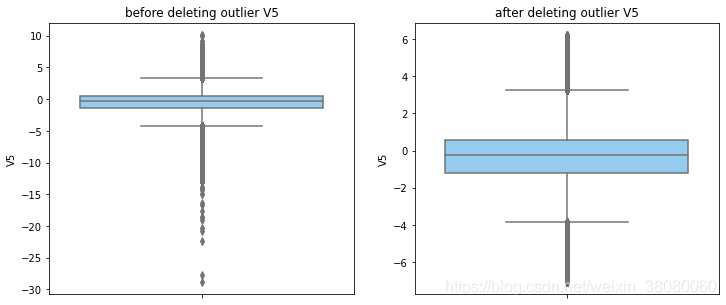
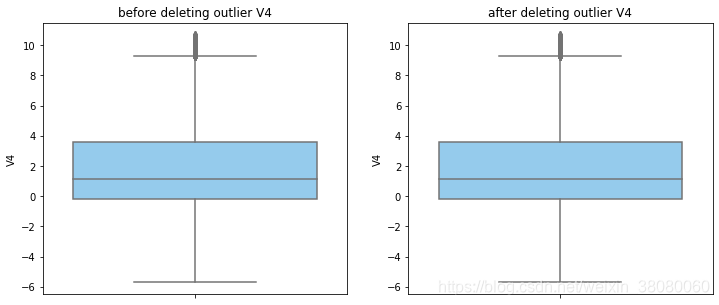
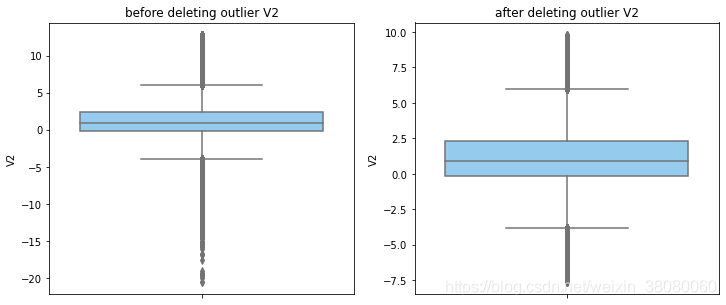
通过分布图可以看到大部分的数值分布较集中,但也存在一些异常值(箱型图和小提琴图看起来更直观),异常值会带偏模型,所以我们需要去除异常值,判断异常值有两种方法:正态分布和上下四分位数。正态分布是采用 3 σ 3\sigma 3σ原则,上下四分位数是利用分位数,超过一分位数或三分位数一定的范围将被确定为异常值
def outlier_process(data,column):Q1 = data[column].quantile(q=0.25)Q3 = data[column].quantile(q=0.75)low_whisker = Q1-3*(Q3-Q1)high_whisker = Q3+3*(Q3-Q1)# 删除异常值data_drop = data[(data[column]>=low_whisker) & (data[column]<=high_whisker)]#画出删除前和删除后的对比图fig,(ax1,ax2) = plt.subplots(1,2,figsize=(12,5))sns.boxplot(y=data[column],ax=ax1,color='lightskyblue')ax1.set_title('before deleting outlier'+' '+column)sns.boxplot(y=data_drop[column],ax=ax2,color='lightskyblue')ax2.set_title('after deleting outlier'+' '+column)return data_drop
numerical_columns = data_rus.columns.drop('Class')
for col_name in numerical_columns:data_rus = outlier_process(data_rus,col_name)
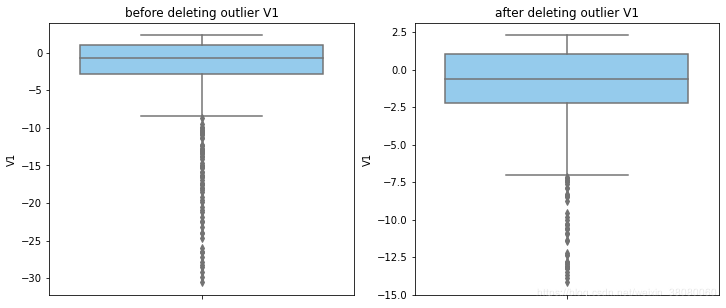
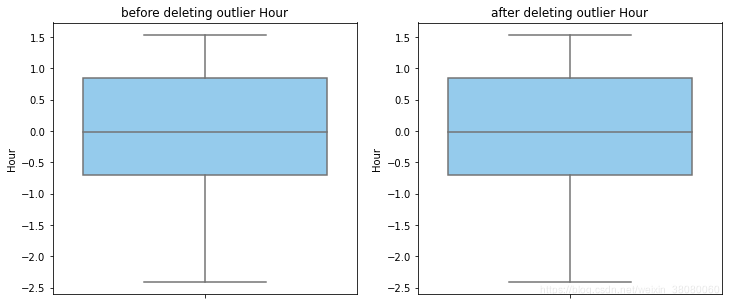
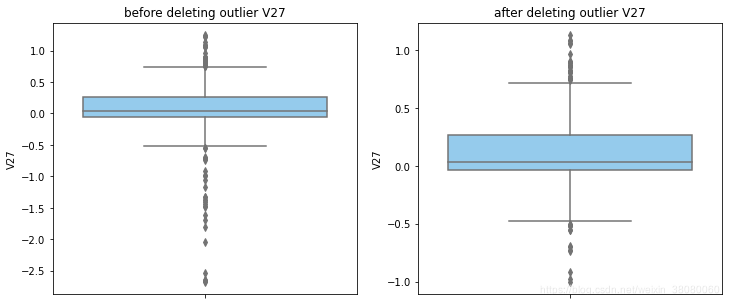
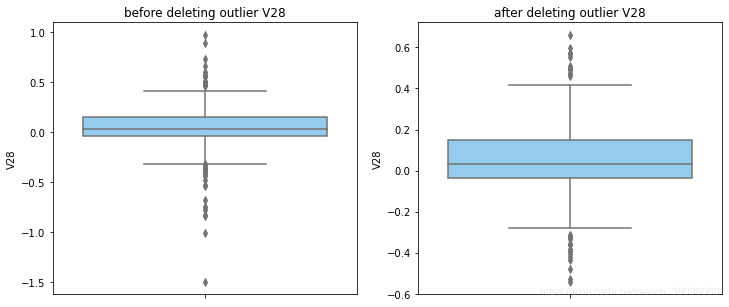
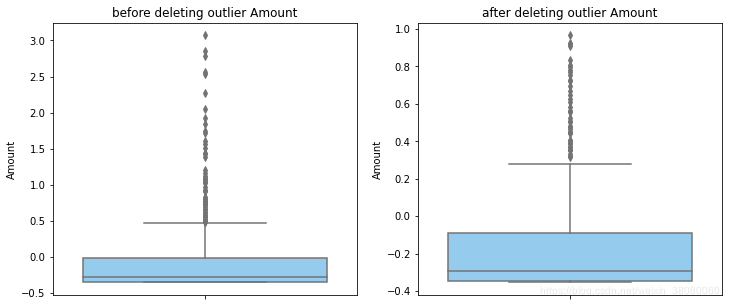
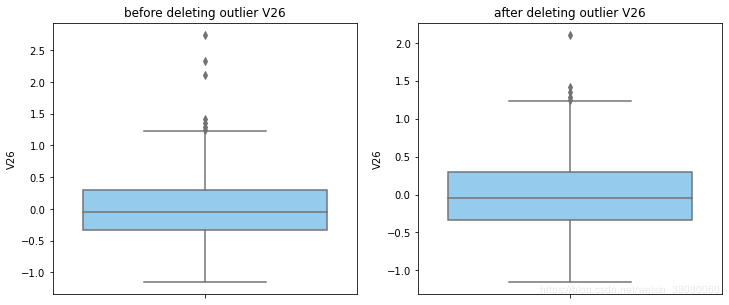
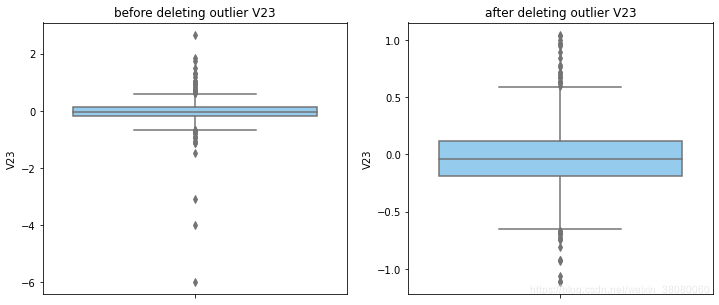
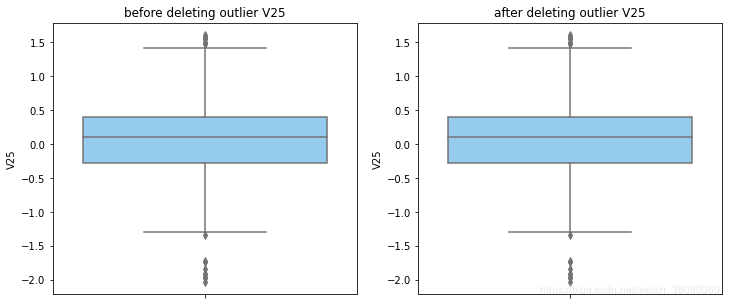
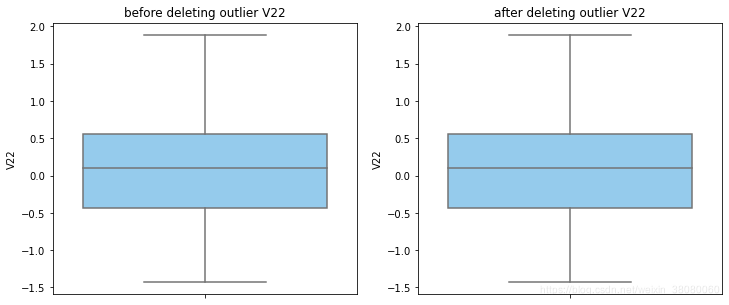
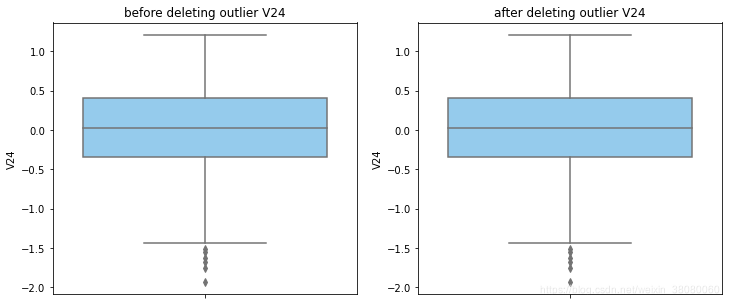
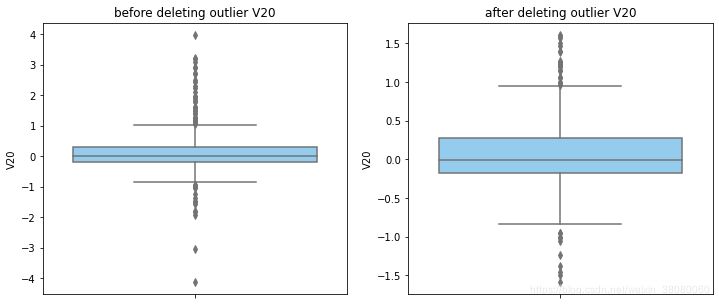
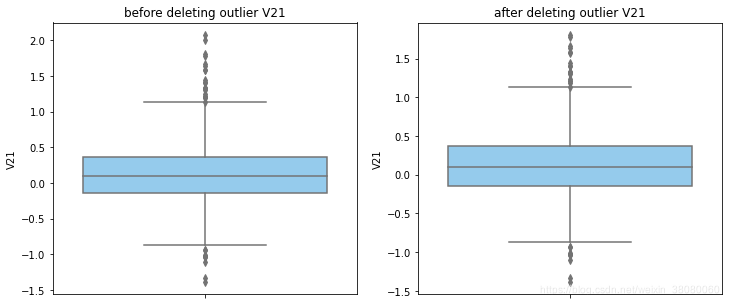
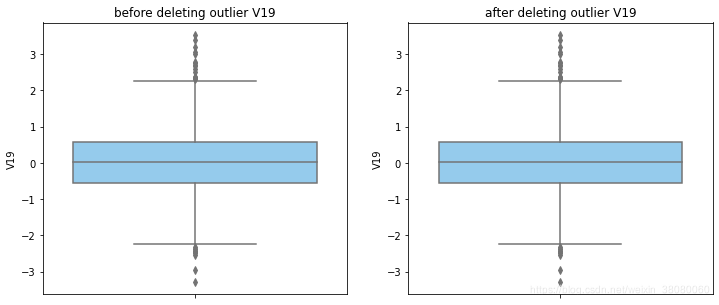
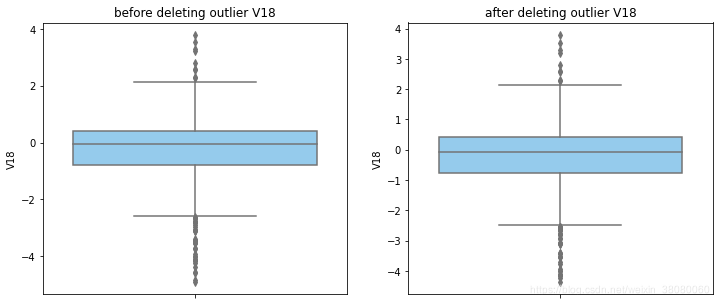
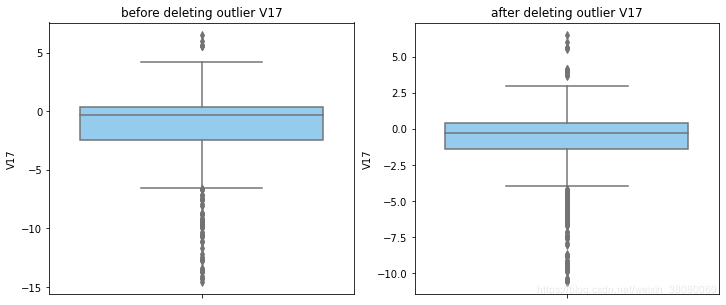
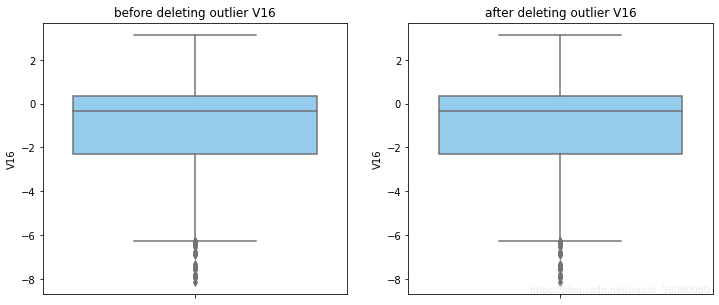
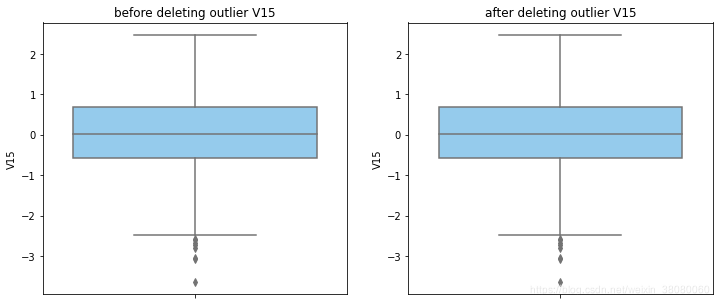
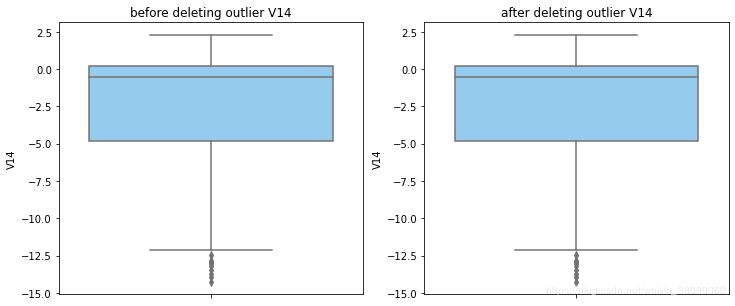
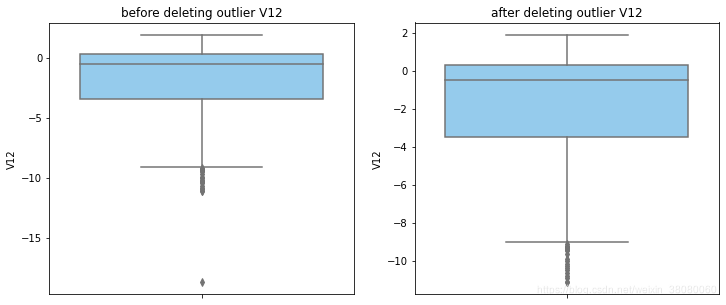
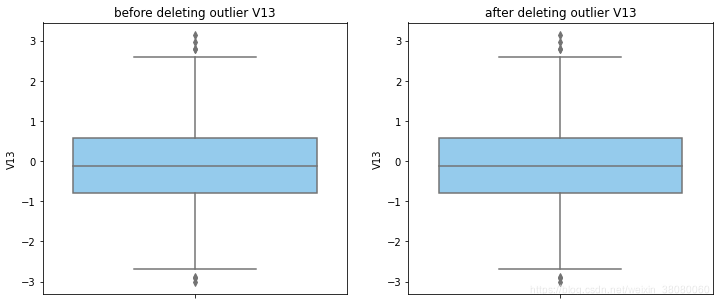
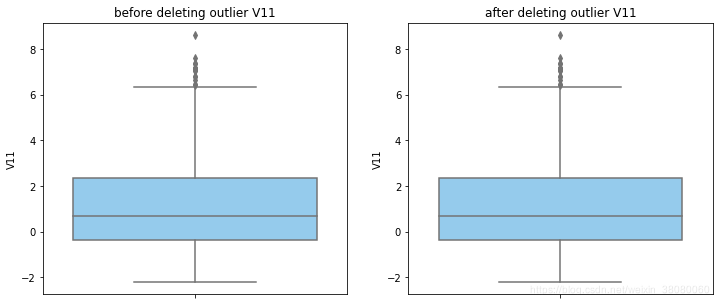
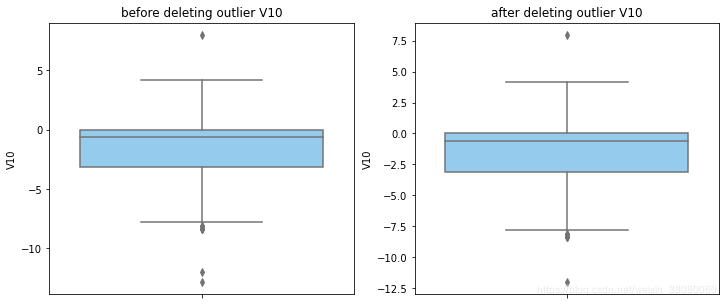
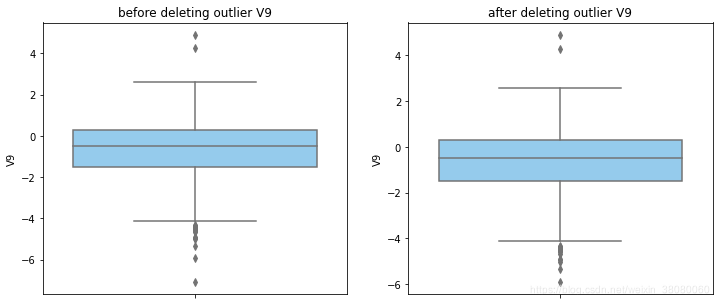

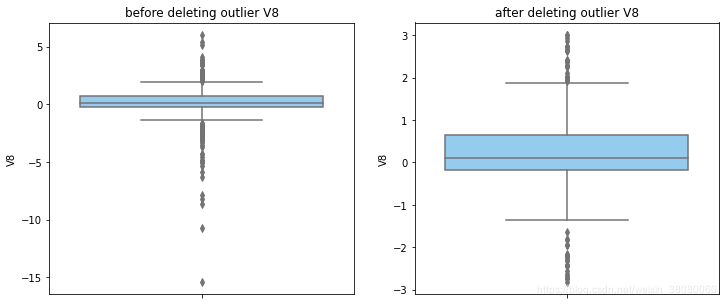
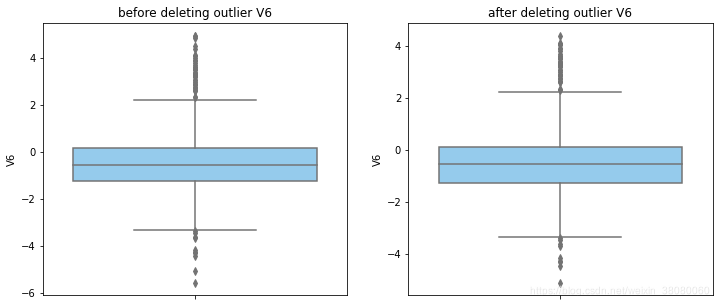
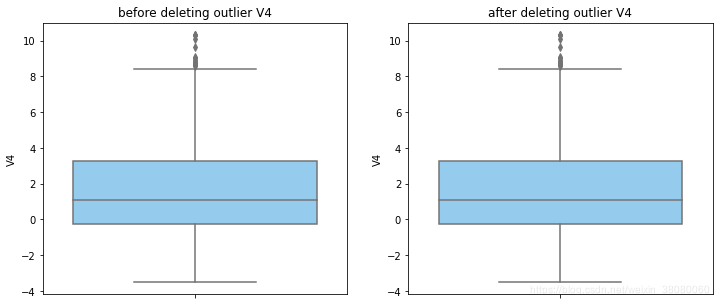

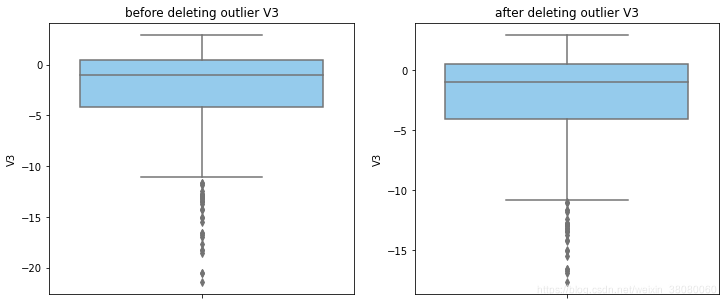
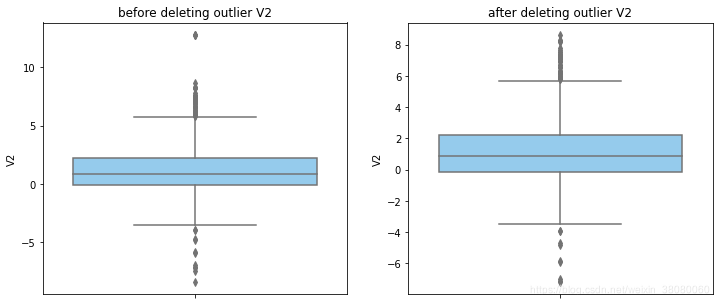
因为有些属性的分布较集中,没有出现太大变化,比如Hour。
清理完脏数据,再探测变量之间的相关关系
#绘制采样前和采样后的热力图
fig,(ax1,ax2) = plt.subplots(2,1,figsize=(10,10))
sns.heatmap(data.corr(),cmap = 'coolwarm_r',ax=ax1,vmax=0.8)
ax1.set_title('the relationship on imbalanced samples')
sns.heatmap(data_rus.corr(),cmap = 'coolwarm_r',ax=ax2,vmax=0.8)
ax2.set_title('the relationship on random under samples')
Text(0.5, 1.0, 'the relationship on random under samples')
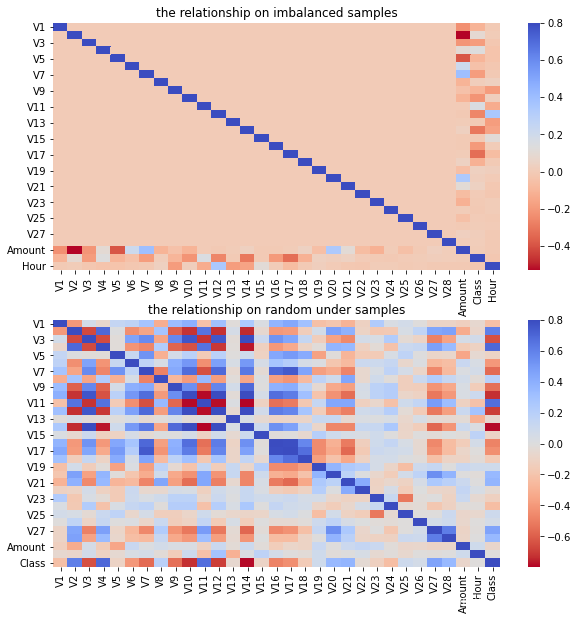
# 分析数值属性与Class之间的相关性
data_rus.corr()['Class'].sort_values(ascending=False)
Class 1.000000
V4 0.722609
V11 0.694975
V2 0.481190
V19 0.245209
V20 0.151424
V21 0.126220
Amount 0.100853
V26 0.090654
V27 0.074491
V8 0.059647
V28 0.052788
V25 0.040578
V22 0.016379
V23 -0.003117
V15 -0.009488
V13 -0.055253
V24 -0.070806
Hour -0.196789
V5 -0.383632
V6 -0.407577
V1 -0.423665
V18 -0.462499
V7 -0.468273
V17 -0.561113
V3 -0.561767
V9 -0.562542
V16 -0.592382
V10 -0.629362
V12 -0.691652
V14 -0.751142
Name: Class, dtype: float64
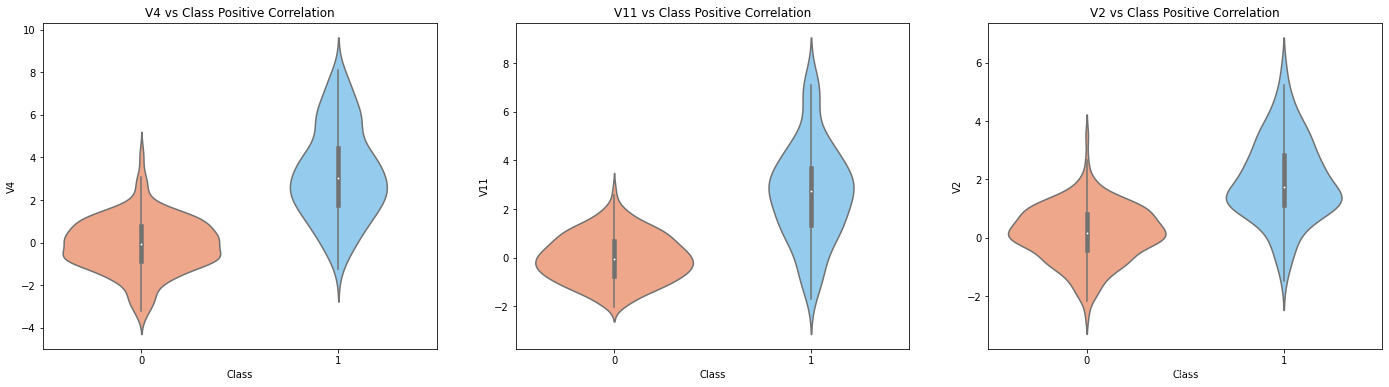
对比可以看到,处理后的数值属性与分类类别之间的相关性明显增加,根据排名,和预测值Class正相关值较大的有V4,V11,V2,V27,负相关值较大的有V_14,V_10,V_12,V_3,V7,V9,我们画出这些特征与预测值之间的关系图
# 正相关的属性与Class分布图
fig,(ax1,ax2,ax3) = plt.subplots(1,3,figsize=(24,6))
sns.violinplot(x='Class',y='V4',data=data_rus,palette=['lightsalmon','lightskyblue'],ax=ax1)
ax1.set_title('V4 vs Class Positive Correlation')sns.violinplot(x='Class',y='V11',data=data_rus,palette=['lightsalmon','lightskyblue'],ax=ax2)
ax2.set_title('V11 vs Class Positive Correlation')sns.violinplot(x='Class',y='V2',data=data_rus,palette=['lightsalmon','lightskyblue'],ax=ax3)
ax3.set_title('V2 vs Class Positive Correlation')
Text(0.5, 1.0, 'V2 vs Class Positive Correlation')
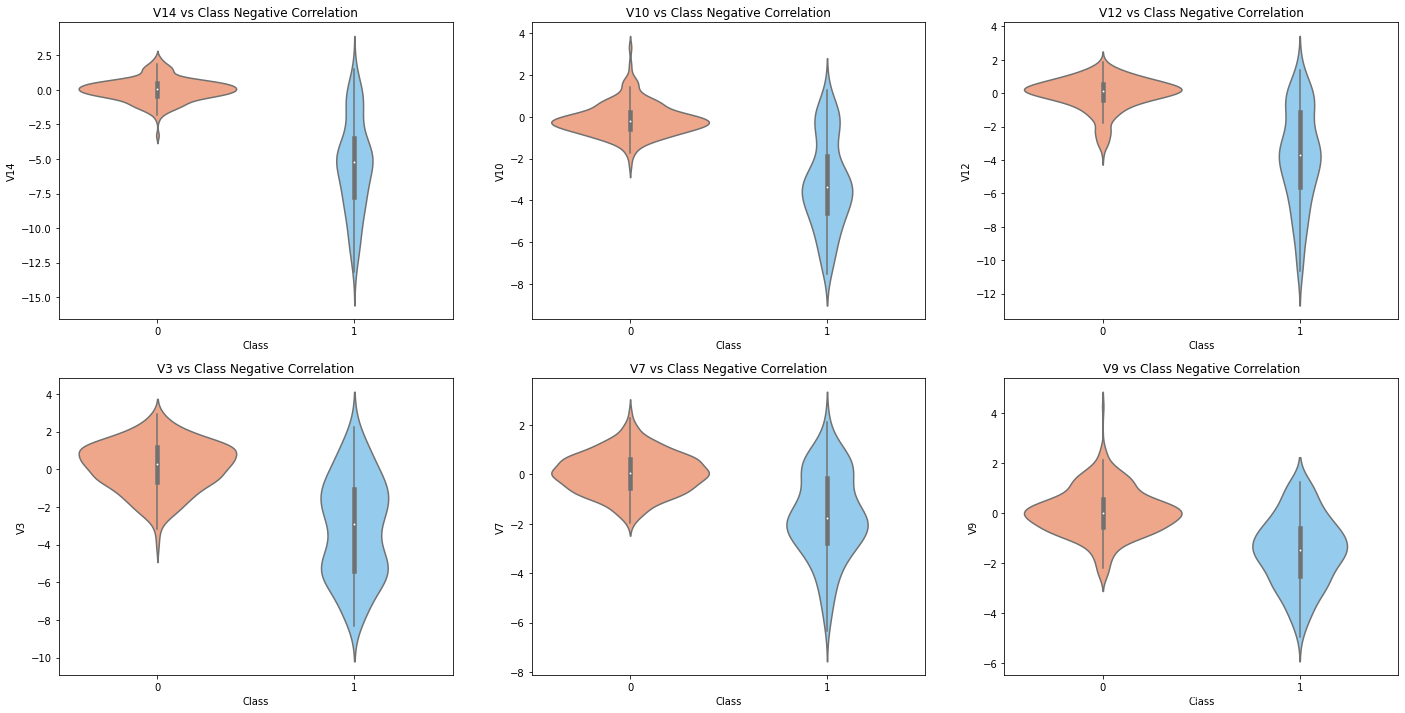
# 负相关的属性与Class分布图
fig,((ax1,ax2,ax3),(ax4,ax5,ax6)) = plt.subplots(2,3,figsize=(24,12))
sns.violinplot(x='Class',y='V14',data=data_rus,palette=['lightsalmon','lightskyblue'],ax=ax1)
ax1.set_title('V14 vs Class Negative Correlation')sns.violinplot(x='Class',y='V10',data=data_rus,palette=['lightsalmon','lightskyblue'],ax=ax2)
ax2.set_title('V10 vs Class Negative Correlation')sns.violinplot(x='Class',y='V12',data=data_rus,palette=['lightsalmon','lightskyblue'],ax=ax3)
ax3.set_title('V12 vs Class Negative Correlation')sns.violinplot(x='Class',y='V3',data=data_rus,palette=['lightsalmon','lightskyblue'],ax=ax4)
ax4.set_title('V3 vs Class Negative Correlation')sns.violinplot(x='Class',y='V7',data=data_rus,palette=['lightsalmon','lightskyblue'],ax=ax5)
ax5.set_title('V7 vs Class Negative Correlation')sns.violinplot(x='Class',y='V9',data=data_rus,palette=['lightsalmon','lightskyblue'],ax=ax6)
ax6.set_title('V9 vs Class Negative Correlation')Text(0.5, 1.0, 'V9 vs Class Negative Correlation')
#其他属性与Class的分布图
other_fea = list(data_rus.columns.drop(['V11','V4','V2','V17','V14','V12','V10','V7','V3','V9','Class']))
fig,ax = plt.subplots(5,4,figsize=(24,36))
for fea in other_fea:sns.violinplot(x='Class',y= fea,data=data_rus,palette=['lightsalmon','lightskyblue'],ax=ax[divmod(other_fea.index(fea),4)[0],divmod(other_fea.index(fea),4)[1]])ax[divmod(other_fea.index(fea),4)[0],divmod(other_fea.index(fea),4)[1]].set_title(fea)
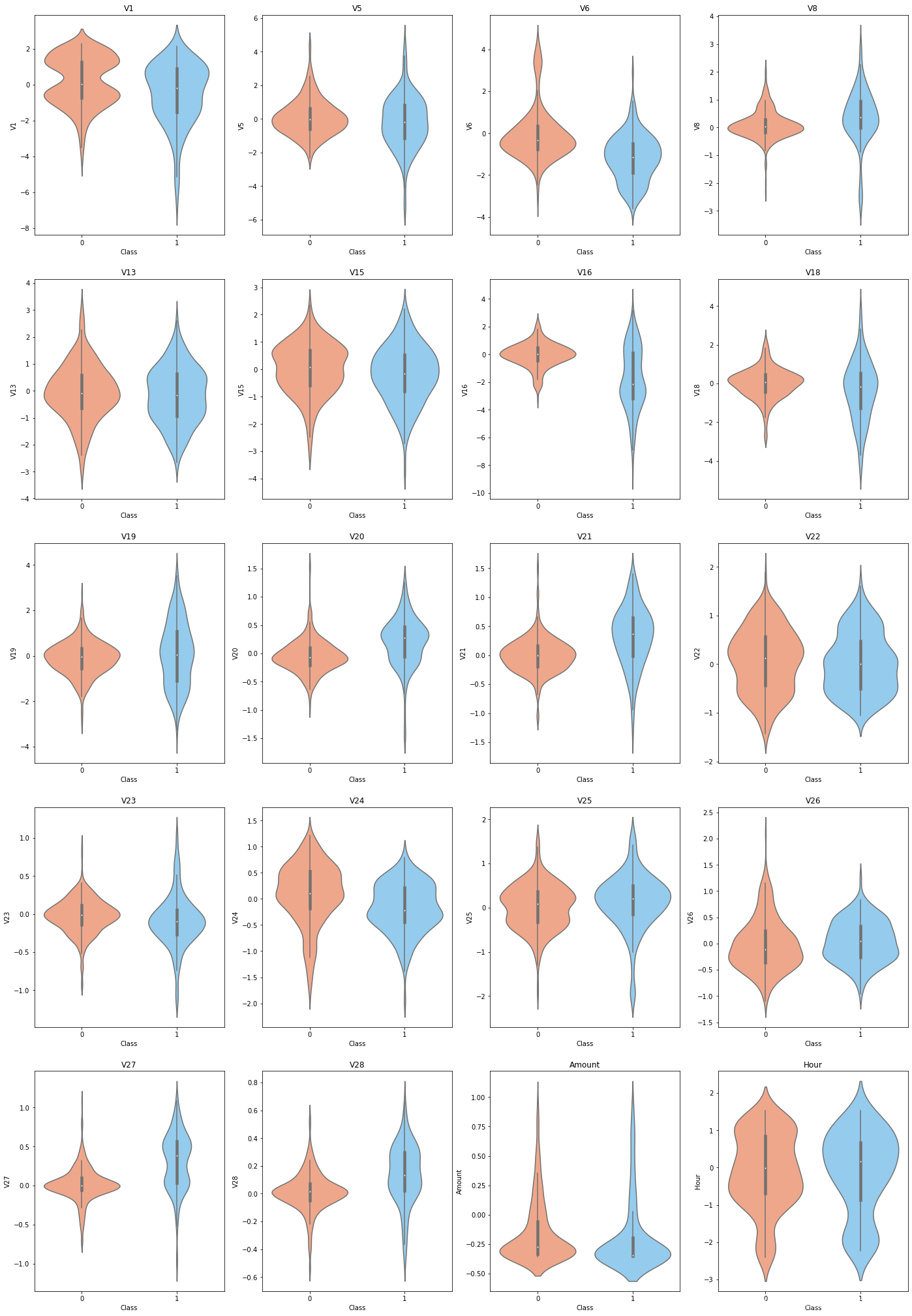
从以上小提琴图可以看出,不同的正负样本在属性值上取值分布确实存在不同,而其他的属性在正负样本上区别相对不大。
好奇金额和时间是否与Class的关系,金额上正常交易金额更少更集中一些,而欺诈交易金额相对较大且分布更散,而时间上正常交易时间跨度小于欺诈交易的时间跨度,所以是在睡觉的时候更可能产生欺诈交易
查看完特征和类别之间的关系,下面分析特征之间的关系,从热力图上可以看出,属性之间是存在相关性的,下面具体看看是否存在多重共线性
sns.set()
sns.pairplot(data[list(data_rus.columns)],kind='scatter',diag_kind = 'kde')
plt.show()

从上图可以看出,这些属性之间不是完全相互独立的,有些存在很强的线性相关性,我们利用方差膨胀系数(VIF)作进一步检验
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = [variance_inflation_factor(data_rus.values, data_rus.columns.get_loc(i)) for i in data_rus.columns]
vif
[12.662373162589994,20.3132501576979,26.78027354608725,9.970255022795625,23.531563683157597,3.4386660732204946,67.84989394913013,5.76519495696649,7.129002458395831,23.226754020950764,11.753104213590975,29.49673779700361,1.3365891898690718,21.57973674600878,1.2669840488461022,27.61485162786757,31.081940593780782,14.088642210869459,2.502857511412321,4.96077803555917,5.169599871511768,3.1235143157354583,2.828445638986856,1.1937601054384332,1.628451339236206,1.1966413137632343,1.959903999050125,1.4573293665681395,6.314999796714301,2.0990707198901117,4.802392100187543]
一般认为 V I F < 10 VIF<10 VIF<10时,该变量与其余变量之间不存在多重共线性,当 10 < V I F < 100 10<VIF<100 10<VIF<100时存在较强的多重共线性,当 V I F > 100 VIF>100 VIF>100时,则认为是存在严重的多重共线性。从以上数值来看,变量之间确实存在多重共线性,也就是存在信息冗余,下面需要进行特征提取或者特征选择
特征提取和特征选择都是降维的两种方法,特征提取所提取的特征是原特征的映射,而特征选择选出的是原特征的子集。主成分分析和线性判别分析是特征提取的两种经典方法。
特征选择:当数据处理完成后,需要选择有意义的特征输入机器学习的算法和模型进行训练,主要从两个方面来选择考虑特征
-
特征是否发散,如果一个特征不发散,例如方差接近0,也就是说样本在这个特征上基本没有差异,这个特征对于样本的区分并没有什么用
-
特征与目标的相关性,与目标相关性高的特征,应当优先选择。
根据特征选择的形式又可以将特征选择分为3种:
1、过滤法:按照发散性或者相关性对各个特征进行评分,设定阈值或带选择阈值的个数,选择特征(方差选择法、相关系数法、卡方检验、互信息法)
2、包装法:根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征(递归特征消除法)
3、嵌入法:先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征,类似于filter方法,但是通过训练来确定特征的优劣(基于惩罚项的特征选择法、基于树模型的特征选择法)
岭回归和Lasso是两种对线性模型特征选择的方法,都是加入正则化项防止过拟合,岭回归加入的是二阶范数的正则化项,而Lasso加入的是一级范式,其中Lasso能够将一些作用比较小的特征的参数训练为0,从而获得稀疏解,也就是在训练模型时实现了降维的目的。
对于树模型,有随机森林分类器对特征的重要性进行排序,可以达到筛选的目的。
本文先采用两种特征选择的方法分别选择出重要的特征,看看特征有什么差别
# 利用Lasso进行特征选择
from sklearn.linear_model import LassoCV
from sklearn.model_selection import cross_val_score
#调用LassoCV函数,并进行交叉验证
model_lasso = LassoCV(alphas=[0.1,0.01,0.005,1],random_state=1,cv=5).fit(X_rus,y_rus)
#输出看模型中最终选择的特征
coef = pd.Series(model_lasso.coef_,index=X_rus.columns)
print(coef[coef != 0].abs().sort_values(ascending = False))
V4 0.062065
V14 0.045851
Amount 0.040011
V26 0.038201
V13 0.031702
V7 0.028889
V22 0.028509
V18 0.028171
V6 0.019226
V1 0.018757
V21 0.016032
V10 0.014742
V28 0.012483
V8 0.011273
V20 0.010726
V9 0.010358
V24 0.010227
V17 0.007217
V2 0.006838
Hour 0.004757
V15 0.003393
V27 0.002588
V19 0.000275
dtype: float64
# 利用随机森林进行特征重要性排序
from sklearn.ensemble import RandomForestClassifier
rfc_fea_model = RandomForestClassifier(random_state=1)
rfc_fea_model.fit(X_rus,y_rus)
fea = X_rus.columns
importance = rfc_fea_model.feature_importances_
a = pd.DataFrame()
a['feature'] = fea
a['importance'] = importance
a = a.sort_values('importance',ascending = False)
plt.figure(figsize=(20,10))
plt.bar(a['feature'],a['importance'])
plt.title('the importance orders sorted by random forest')
plt.show()

a.cumsum()
| feature | importance | |
|---|---|---|
| 11 | V12 | 0.134515 |
| 9 | V12V10 | 0.268117 |
| 16 | V12V10V17 | 0.388052 |
| 13 | V12V10V17V14 | 0.503750 |
| 3 | V12V10V17V14V4 | 0.615973 |
| 10 | V12V10V17V14V4V11 | 0.687904 |
| 1 | V12V10V17V14V4V11V2 | 0.731179 |
| 15 | V12V10V17V14V4V11V2V16 | 0.774247 |
| 2 | V12V10V17V14V4V11V2V16V3 | 0.813352 |
| 6 | V12V10V17V14V4V11V2V16V3V7 | 0.846050 |
| 18 | V12V10V17V14V4V11V2V16V3V7V19 | 0.860559 |
| 17 | V12V10V17V14V4V11V2V16V3V7V19V18 | 0.873657 |
| 20 | V12V10V17V14V4V11V2V16V3V7V19V18V21 | 0.886416 |
| 28 | V12V10V17V14V4V11V2V16V3V7V19V18V21Amount | 0.896986 |
| 26 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27 | 0.906369 |
| 19 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20 | 0.915172 |
| 14 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15 | 0.923700 |
| 22 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23 | 0.931990 |
| 12 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13 | 0.939298 |
| 7 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8 | 0.946163 |
| 5 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8V6 | 0.952952 |
| 25 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8V6V26 | 0.959418 |
| 8 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8V6V26V9 | 0.965869 |
| 0 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8V6V26V9V1 | 0.971975 |
| 4 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8V6V26V9V1V5 | 0.977297 |
| 21 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8V6V26V9V1V5V22 | 0.982325 |
| 27 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8V6V26V9V1V5V22V28 | 0.986990 |
| 23 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8V6V26V9V1V5V22V28V24 | 0.991551 |
| 29 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8V6V26V9V1V5V22V28V24Hour | 0.995913 |
| 24 | V12V10V17V14V4V11V2V16V3V7V19V18V21AmountV27V20V15V23V13V8V6V26V9V1V5V22V28V24HourV25 | 1.000000 |
从以上结果来看,两种方法的排序,特征重要性差别很大,为了更大程度的保留数据的信息,我们采用两种结合的特征,包括[‘V14’,‘V12’,‘V10’,‘V17’,‘V4’,‘V11’,‘V3’,‘V2’,‘V7’,‘V16’,‘V18’,‘Amount’,‘V19’,‘V20’,‘V23’,‘V21’,‘V15’,‘V9’,‘V6’,‘V27’,‘V25’,‘V5’,‘V13’,‘V22’,‘Hour’,‘V28’,‘V1’,‘V8’,‘V26’],其中选择的标准是随机森林中重要性总和95%以上,如果其中有Lasso回归没有的,则加入,共选出29个特征(只有V24没有被选择)
# 使用选择的特征采进行训练和测试
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import classification_report
from sklearn.linear_model import LogisticRegression # 逻辑回归
from sklearn.neighbors import KNeighborsClassifier # KNN
from sklearn.naive_bayes import GaussianNB # 朴素贝叶斯
from sklearn.svm import SVC # 支持向量分类
from sklearn.tree import DecisionTreeClassifier # 决策树
from sklearn.ensemble import RandomForestClassifier # 随机森林
from sklearn.ensemble import AdaBoostClassifier # Adaboost
from sklearn.ensemble import GradientBoostingClassifier # GBDT
from xgboost import XGBClassifier # XGBoost
from lightgbm import LGBMClassifier # lightGBM
from sklearn.metrics import roc_curve # 绘制ROC曲线
Classifiers = {'LG': LogisticRegression(random_state=1),'KNN': KNeighborsClassifier(),'Bayes': GaussianNB(),'SVC': SVC(random_state=1,probability=True),'DecisionTree': DecisionTreeClassifier(random_state=1),'RandomForest': RandomForestClassifier(random_state=1),'Adaboost':AdaBoostClassifier(random_state=1),'GBDT': GradientBoostingClassifier(random_state=1),'XGboost': XGBClassifier(random_state=1),'LightGBM': LGBMClassifier(random_state=1)}
def train_test(Classifiers, X_train, y_train, X_test, y_test):y_pred = pd.DataFrame()Accuracy_Score = pd.DataFrame()
# score.model_name = Classifiers.keysfor model_name, model in Classifiers.items():model.fit(X_train, y_train)y_pred[model_name] = model.predict(X_test)y_pred_pra = model.predict_proba(X_test)Accuracy_Score[model_name] = pd.Series(model.score(X_test, y_test))# 计算召回率print(model_name, '\n', classification_report(y_test, y_pred[model_name]))
# confu_mat = confusion_matrix(y_test,y_pred[model_name])
# plt.matshow(confu_mat,cmap = plt.cm.Blues)
# plt.title(model_name)
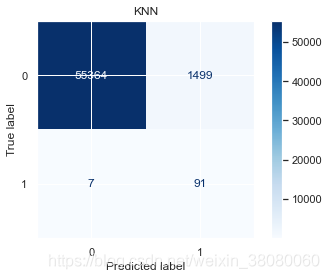
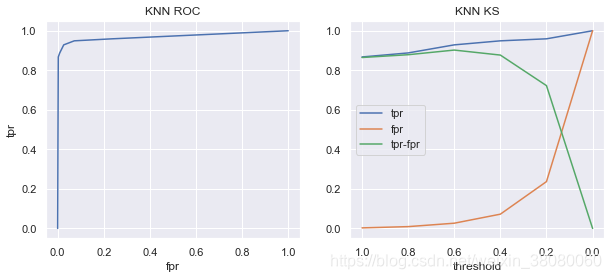
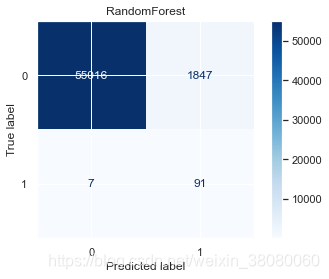
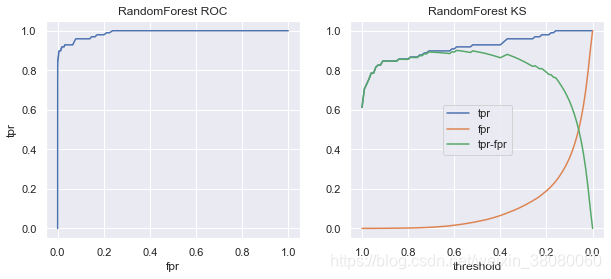
# plt.colorbar()# 画出混淆矩阵fig, ax = plt.subplots(1, 1)plot_confusion_matrix(model, X_test, y_test, labels=[0, 1], cmap='Blues', ax=ax)ax.set_title(model_name)# 画出roc曲线plt.figure()fig,(ax1,ax2) = plt.subplots(1,2,figsize=(10,4))fpr, tpr, thres = roc_curve(y_test, y_pred_pra[:, -1])ax1.plot(fpr, tpr)ax1.set_title(model_name+' ROC')ax1.set_xlabel('fpr')ax1.set_ylabel('tpr')# 画出KS曲线ax2.plot(thres[1:],tpr[1:])ax2.plot(thres[1:],fpr[1:])ax2.plot(thres[1:],tpr[1:]-fpr[1:])ax2.set_xlabel('threshold')ax2.legend(['tpr','fpr','tpr-fpr'])plt.sca(ax2)plt.gca().invert_xaxis()
# ax2.gca().invert_xaxis()ax2.set_title(model_name+' KS')return y_pred,Accuracy_Score# test_cols = ['V12', 'V14', 'V10', 'V17', 'V11', 'V4', 'V2', 'V16', 'V7', 'V3',
# 'V18', 'Amount', 'V19', 'V21', 'V20', 'V8', 'V15', 'V6', 'V27', 'V26', 'V1','V9','V13','V22','Hour','V23','V28']
test_cols = X_rus.columns.drop('V24')
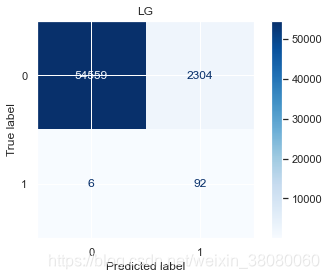
Y_pred,Accuracy_score = train_test(Classifiers, X_rus[test_cols], y_rus, X_test[test_cols], y_test)
Accuracy_score
LGprecision recall f1-score support0 1.00 0.96 0.98 568631 0.04 0.94 0.07 98accuracy 0.96 56961macro avg 0.52 0.95 0.53 56961
weighted avg 1.00 0.96 0.98 56961KNNprecision recall f1-score support0 1.00 0.97 0.99 568631 0.06 0.93 0.11 98accuracy 0.97 56961macro avg 0.53 0.95 0.55 56961
weighted avg 1.00 0.97 0.99 56961Bayesprecision recall f1-score support0 1.00 0.96 0.98 568631 0.04 0.88 0.08 98accuracy 0.96 56961macro avg 0.52 0.92 0.53 56961
weighted avg 1.00 0.96 0.98 56961SVCprecision recall f1-score support0 1.00 0.98 0.99 568631 0.08 0.91 0.14 98accuracy 0.98 56961macro avg 0.54 0.94 0.57 56961
weighted avg 1.00 0.98 0.99 56961DecisionTreeprecision recall f1-score support0 1.00 0.88 0.93 568631 0.01 0.95 0.03 98accuracy 0.88 56961macro avg 0.51 0.91 0.48 56961
weighted avg 1.00 0.88 0.93 56961RandomForestprecision recall f1-score support0 1.00 0.97 0.98 568631 0.05 0.93 0.09 98accuracy 0.97 56961macro avg 0.52 0.95 0.54 56961
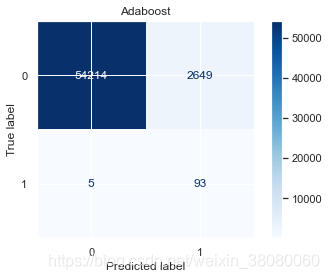
weighted avg 1.00 0.97 0.98 56961Adaboostprecision recall f1-score support0 1.00 0.95 0.98 568631 0.03 0.95 0.07 98accuracy 0.95 56961macro avg 0.52 0.95 0.52 56961
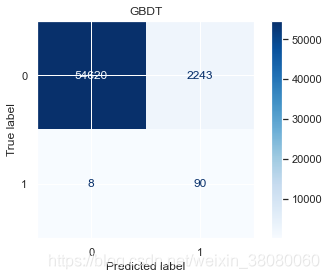
weighted avg 1.00 0.95 0.97 56961GBDTprecision recall f1-score support0 1.00 0.96 0.98 568631 0.04 0.92 0.07 98accuracy 0.96 56961macro avg 0.52 0.94 0.53 56961
weighted avg 1.00 0.96 0.98 56961[15:05:57] WARNING: C:/Users/Administrator/workspace/xgboost-win64_release_1.4.0/src/learner.cc:1095: Starting in XGBoost 1.3.0, the default evaluation metric used with the objective 'binary:logistic' was changed from 'error' to 'logloss'. Explicitly set eval_metric if you'd like to restore the old behavior.
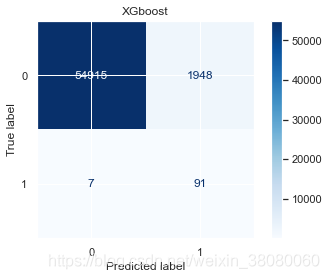
XGboostprecision recall f1-score support0 1.00 0.97 0.98 568631 0.04 0.93 0.09 98accuracy 0.97 56961macro avg 0.52 0.95 0.53 56961
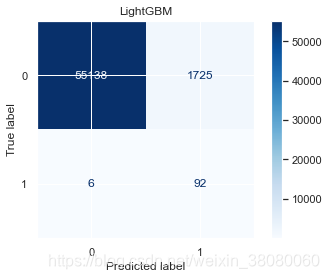
weighted avg 1.00 0.97 0.98 56961LightGBMprecision recall f1-score support0 1.00 0.97 0.98 568631 0.05 0.94 0.10 98accuracy 0.97 56961macro avg 0.53 0.95 0.54 56961
weighted avg 1.00 0.97 0.98 56961
| LG | KNN | Bayes | SVC | DecisionTree | RandomForest | Adaboost | GBDT | XGboost | LightGBM | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.959446 | 0.973561 | 0.962887 | 0.981479 | 0.877899 | 0.967451 | 0.953407 | 0.960482 | 0.965678 | 0.969611 |
<Figure size 432x288 with 0 Axes>

<Figure size 432x288 with 0 Axes>



# 集成学习
# 根据以上auc以及recall的结果,选择LG,DT以及GBDT当作基模型
from sklearn.ensemble import VotingClassifier
voting_clf = VotingClassifier(estimators=[
# ('LG', LogisticRegression(random_state=1)),('KNN', KNeighborsClassifier()),
# ('Bayes',GaussianNB()),('SVC', SVC(random_state=1,probability=True)),
# ('DecisionTree', DecisionTreeClassifier(random_state=1)),
# ('RandomForest', RandomForestClassifier(random_state=1)),
# ('Adaboost',AdaBoostClassifier(random_state=1)),
# ('GBDT', GradientBoostingClassifier(random_state=1)),
# ('XGboost', XGBClassifier(random_state=1)),('LightGBM', LGBMClassifier(random_state=1))])
voting_clf.fit(X_rus[test_cols], y_rus)
y_final_pred = voting_clf.predict(X_test[test_cols])
print(classification_report(y_test, y_final_pred))
fig, ax = plt.subplots(1, 1)
plot_confusion_matrix(voting_clf, X_test[test_cols], y_test, labels=[0, 1], cmap='Blues', ax=ax)
precision recall f1-score support0 1.00 0.98 0.99 568631 0.08 0.94 0.14 98accuracy 0.98 56961macro avg 0.54 0.96 0.57 56961
weighted avg 1.00 0.98 0.99 56961<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x213686f0700>
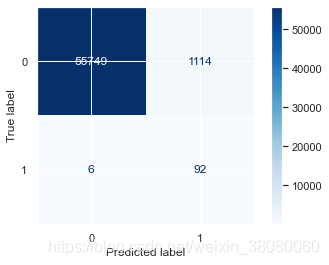
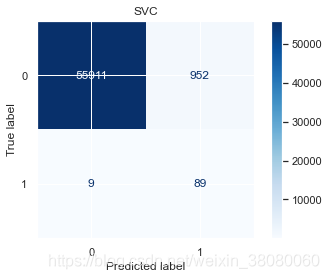
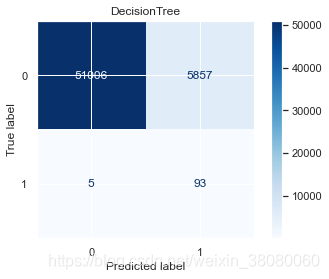
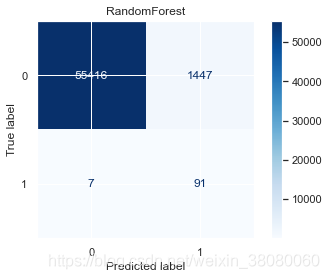
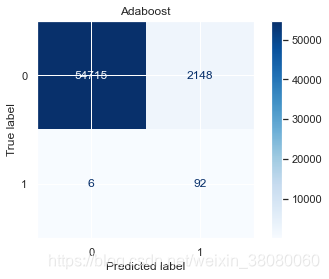
通过以上结果,模型的精确度accuracy都挺高的,尤其是支持向量分类的达到了98.1479%,但对于不平衡样本来说,更应该关注召回率,在SVC中,识别出欺诈交易的概率是91%,而对于非欺诈样本的识别率是99%,分别有1046和9份样本识别错误。
在进行模型调优之前,尝试着用默认参数来构成模型集成,选择出精确度高的3个模型,KNN,SVC,和Light GBM,得到的结果的精确度是98%,分别有6份和1114份样本识别错误,在欺诈样本的识别上有所提升,但是非欺诈样本检测成欺诈样本数量增加了。
因为模型中使用的参数都是默认的,考虑利用网格搜索确定最佳参数,当然网格搜索也不一定能找到最好的参数
初步模型已经建立,但是模型的参数采用的是模型默认的,下面进行调参。调参的方法有三种:随机搜索、网格搜索以及贝叶斯优化。而随即搜索和网格搜索当超参数过多时,极其耗时,因为他们的搜索次数是所有参数的组合,而利用贝叶斯优化进行调参会考虑之前的参数信息,不断更新先验,且迭代次数少,速度快。
# 网格搜索找最佳参数
from sklearn.model_selection import GridSearchCV
def reg_best(X_train, y_train):log_reg_parames = {'penalty': ['l1', 'l2'],'C': [0.001, 0.01, 0.05, 0.1, 1, 10]}grid_log_reg = GridSearchCV(LogisticRegression(), log_reg_parames)grid_log_reg.fit(X_train, y_train)log_reg_best = grid_log_reg.best_estimator_print(log_reg_best)return log_reg_bestdef KNN_best(X_train, y_train):KNN_parames = {'n_neighbors': [3, 5, 7, 9, 11, 15], 'algorithm': ['auto', 'ball_tree', 'kd_tree', 'brute']}grid_KNN = GridSearchCV(KNeighborsClassifier(), KNN_parames)grid_KNN.fit(X_train, y_train)KNN_best_ = grid_KNN.best_estimator_print(KNN_best_)return KNN_best_def SVC_best(X_train, y_train):SVC_parames = {'C': [0.5, 0.7, 0.9, 1], 'kernel': ['rbf', 'poly', 'sigmoid', 'linear'], 'probability': [True]}grid_SVC = GridSearchCV(SVC(), SVC_parames)grid_SVC.fit(X_train, y_train)SVC_best = grid_SVC.best_estimator_print(SVC_best)return SVC_bestdef DecisionTree_best(X_train, y_train):DT_parames = {"criterion": ["gini", "entropy"], "max_depth": list(range(2, 4, 1)),"min_samples_leaf": list(range(5, 7, 1))}grid_DT = GridSearchCV(DecisionTreeClassifier(), DT_parames)grid_DT.fit(X_train, y_train)DT_best = grid_DT.best_estimator_print(DT_best)return DT_bestdef RandomForest_best(X_train, y_train):RF_params = {'n_estimators': [10, 50, 100, 150, 200], 'criterion': ['gini', 'entropy'], "min_samples_leaf": list(range(5, 7, 1))}grid_RF = GridSearchCV(RandomForestClassifier(), RF_params)grid_RF.fit(X_train, y_train)RT_best = grid_RF.best_estimator_print(RT_best)return RT_bestdef Adaboost_best(X_train, y_train):Adaboost_params = {'n_estimators': [10, 50, 100, 150, 200], 'learning_rate': [0.01, 0.05, 0.1, 0.5, 1], 'algorithm': ['SAMME', 'SAMME.R']}grid_Adaboost = GridSearchCV(AdaBoostClassifier(), Adaboost_params)grid_Adaboost.fit(X_train, y_train)Adaboost_best_ = grid_Adaboost.best_estimator_print(Adaboost_best_)return Adaboost_best_def GBDT_best(X_train, y_train):GBDT_params = {'n_estimators': [10, 50, 100, 150], 'loss': ['deviance', 'exponential'], 'learning_rate': [0.01, 0.05, 0.1], 'criterion': ['friedman_mse', 'mse']}grid_GBDT = GridSearchCV(GradientBoostingClassifier(), GBDT_params)grid_GBDT.fit(X_train, y_train)GBDT_best_ = grid_GBDT.best_estimator_print(GBDT_best_)return GBDT_best_def XGboost_best(X_train, y_train):XGB_params = {'n_estimators': [10, 50, 100, 150, 200], 'max_depth': [5, 10, 15, 20], 'learning_rate': [0.01, 0.05, 0.1, 0.5, 1]}grid_XGB = GridSearchCV(XGBClassifier(), XGB_params)grid_XGB.fit(X_train, y_train)XGB_best_ = grid_XGB.best_estimator_print(XGB_best_)return XGB_best_def LGBM_best(X_train, y_train):LGBM_params = {'boosting_type': ['gbdt', 'dart', 'goss', 'rf'], 'num_leaves': [21, 31, 51], 'n_estimators': [10, 50, 100, 150, 200], 'max_depth': [5, 10, 15, 20], 'learning_rate': [0.01, 0.05, 0.1, 0.5, 1]}grid_LGBM = GridSearchCV(LGBMClassifier(), LGBM_params)grid_LGBM.fit(X_train, y_train)LGBM_best_ = grid_LGBM.best_estimator_print(LGBM_best_)return LGBM_best_
Classifiers = {'LG': reg_best(X_rus[test_cols], y_rus),'KNN': KNN_best(X_rus[test_cols], y_rus),'Bayes': GaussianNB(),'SVC': SVC_best(X_rus[test_cols], y_rus),'DecisionTree': DecisionTree_best(X_rus[test_cols], y_rus),'RandomForest': RandomForest_best(X_rus[test_cols], y_rus),'Adaboost':Adaboost_best(X_rus[test_cols], y_rus),'GBDT': GBDT_best(X_rus[test_cols], y_rus),'XGboost': XGboost_best(X_rus[test_cols], y_rus),'LightGBM': LGBM_best(X_rus[test_cols], y_rus)}LogisticRegression(C=0.05)
KNeighborsClassifier(n_neighbors=3)
SVC(C=0.7, probability=True)
DecisionTreeClassifier(criterion='entropy', max_depth=2, min_samples_leaf=5)
RandomForestClassifier(min_samples_leaf=5)
AdaBoostClassifier(algorithm='SAMME', learning_rate=0.5, n_estimators=100)
GradientBoostingClassifier(criterion='mse', loss='exponential')
XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,colsample_bynode=1, colsample_bytree=1, gamma=0, gpu_id=-1,importance_type='gain', interaction_constraints='',learning_rate=0.5, max_delta_step=0, max_depth=5,min_child_weight=1, missing=nan, monotone_constraints='()',n_estimators=10, n_jobs=8, num_parallel_tree=1, random_state=0,reg_alpha=0, reg_lambda=1, scale_pos_weight=1, subsample=1,tree_method='exact', validate_parameters=1, verbosity=None)
LGBMClassifier(boosting_type='dart', learning_rate=1, max_depth=5,n_estimators=150, num_leaves=21)
# 利用优化后的参数再训练测试
Y_pred,Accuracy_score = train_test(Classifiers, X_rus[test_cols], y_rus, X_test[test_cols], y_test)
Accuracy_score
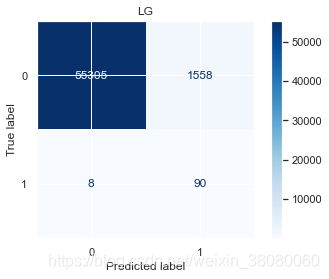
LGprecision recall f1-score support0 1.00 0.97 0.99 568631 0.05 0.92 0.10 98accuracy 0.97 56961macro avg 0.53 0.95 0.54 56961
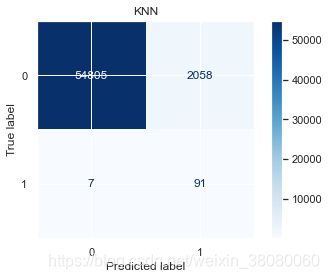
weighted avg 1.00 0.97 0.98 56961KNNprecision recall f1-score support0 1.00 0.96 0.98 568631 0.04 0.93 0.08 98accuracy 0.96 56961macro avg 0.52 0.95 0.53 56961
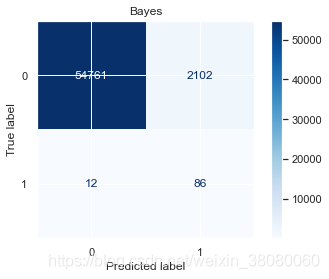
weighted avg 1.00 0.96 0.98 56961Bayesprecision recall f1-score support0 1.00 0.96 0.98 568631 0.04 0.88 0.08 98accuracy 0.96 56961macro avg 0.52 0.92 0.53 56961
weighted avg 1.00 0.96 0.98 56961SVCprecision recall f1-score support0 1.00 0.98 0.99 568631 0.09 0.91 0.16 98accuracy 0.98 56961macro avg 0.54 0.95 0.57 56961
weighted avg 1.00 0.98 0.99 56961DecisionTreeprecision recall f1-score support0 1.00 0.90 0.95 568631 0.02 0.95 0.03 98accuracy 0.90 56961macro avg 0.51 0.92 0.49 56961
weighted avg 1.00 0.90 0.94 56961RandomForestprecision recall f1-score support0 1.00 0.97 0.99 568631 0.06 0.93 0.11 98accuracy 0.97 56961macro avg 0.53 0.95 0.55 56961
weighted avg 1.00 0.97 0.99 56961Adaboostprecision recall f1-score support0 1.00 0.96 0.98 568631 0.04 0.94 0.08 98accuracy 0.96 56961macro avg 0.52 0.95 0.53 56961
weighted avg 1.00 0.96 0.98 56961GBDTprecision recall f1-score support0 1.00 0.97 0.98 568631 0.05 0.93 0.09 98accuracy 0.97 56961macro avg 0.52 0.95 0.53 56961
weighted avg 1.00 0.97 0.98 56961[15:36:45] WARNING: C:/Users/Administrator/workspace/xgboost-win64_release_1.4.0/src/learner.cc:1095: Starting in XGBoost 1.3.0, the default evaluation metric used with the objective 'binary:logistic' was changed from 'error' to 'logloss'. Explicitly set eval_metric if you'd like to restore the old behavior.
XGboostprecision recall f1-score support0 1.00 0.96 0.98 568631 0.04 0.93 0.07 98accuracy 0.96 56961macro avg 0.52 0.94 0.53 56961
weighted avg 1.00 0.96 0.98 56961LightGBMprecision recall f1-score support0 1.00 0.97 0.98 568631 0.05 0.93 0.10 98accuracy 0.97 56961macro avg 0.53 0.95 0.54 56961
weighted avg 1.00 0.97 0.98 56961
| LG | KNN | Bayes | SVC | DecisionTree | RandomForest | Adaboost | GBDT | XGboost | LightGBM | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.972508 | 0.963747 | 0.962887 | 0.983129 | 0.897087 | 0.974474 | 0.962185 | 0.966152 | 0.960043 | 0.969769 |
<Figure size 432x288 with 0 Axes>
<Figure size 432x288 with 0 Axes>
<Figure size 432x288 with 0 Axes>
<Figure size 432x288 with 0 Axes>
<Figure size 432x288 with 0 Axes>
<Figure size 432x288 with 0 Axes>
<Figure size 432x288 with 0 Axes>
<Figure size 432x288 with 0 Axes>
<Figure size 432x288 with 0 Axes>

<Figure size 432x288 with 0 Axes>
# 集成学习
# 根据以上auc以及recall的结果,选择LG,DT以及GBDT当作基模型
from sklearn.ensemble import VotingClassifier
voting_clf = VotingClassifier(estimators=[('LG', LogisticRegression(random_state=1,C=0.05)),('SVC', SVC(random_state=1,probability=True,C=0.7)),('RandomForest', RandomForestClassifier(random_state=1,min_samples_leaf=5)),])
voting_clf.fit(X_rus[test_cols], y_rus)
y_final_pred=voting_clf.predict(X_test[test_cols])
print(classification_report(y_test, y_final_pred))
fig, ax=plt.subplots(1, 1)
plot_confusion_matrix(voting_clf, X_test[test_cols], y_test, labels=[0, 1], cmap='Blues', ax=ax)
precision recall f1-score support0 1.00 0.98 0.99 568631 0.07 0.92 0.14 98accuracy 0.98 56961macro avg 0.54 0.95 0.56 56961
weighted avg 1.00 0.98 0.99 56961<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x2135666d070>
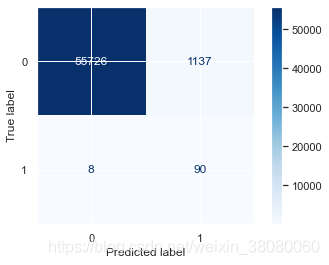
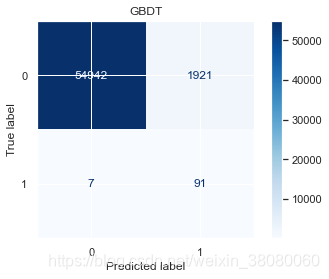
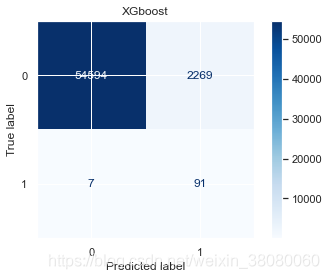
从精确度上来看,大部分模型都有提升,也有一些模型的精确度是退化的。在召回率上没有明显提升,甚至有些退化比较明显,这说明对于欺诈样本的识别还是不够明显。因为采用的训练样本数远小于测试样本数,这也导致了测试效果不行。
SMOTE上采样与随机下采样相结合
还是对训练样本进行分析再训练模型
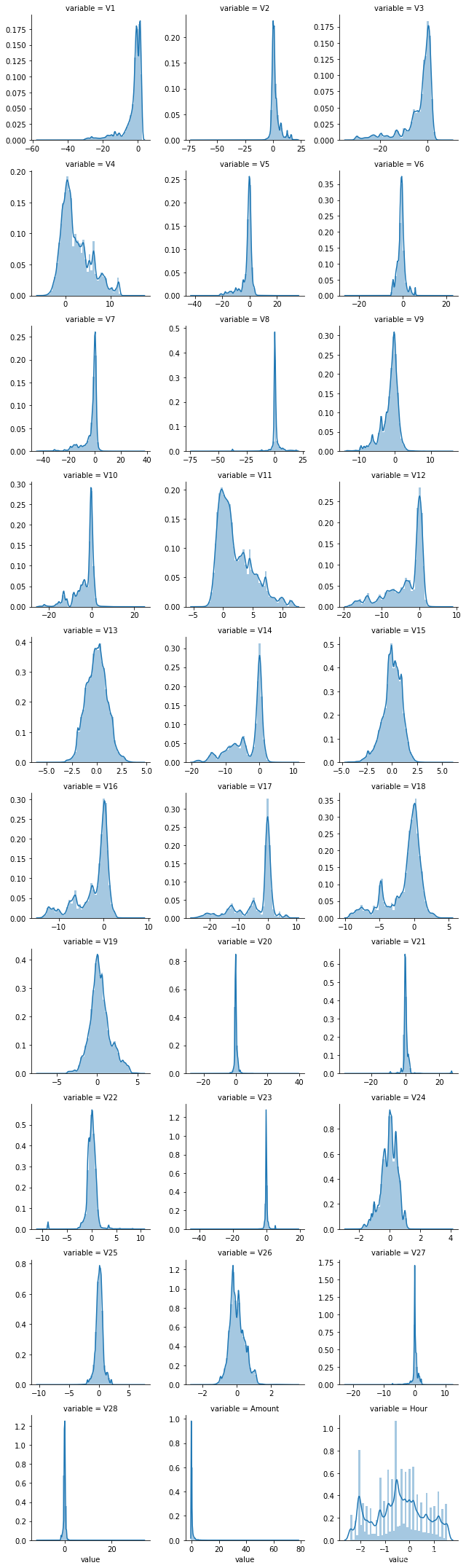
data_smote = pd.concat([X_smote,y_smote],axis=1)
# 单个数值特征分布情况
f = pd.melt(data_smote, value_vars=X_train.columns)
g = sns.FacetGrid(f, col='variable', col_wrap=3, sharex=False, sharey=False)
g = g.map(sns.distplot, 'value')
# 单个数值特征分布箱线图
f = pd.melt(data_smote, value_vars=X_train.columns)
g = sns.FacetGrid(f,col='variable', col_wrap=3, sharex=False, sharey=False,size=5)
g = g.map(sns.boxplot, 'value', color='lightskyblue')
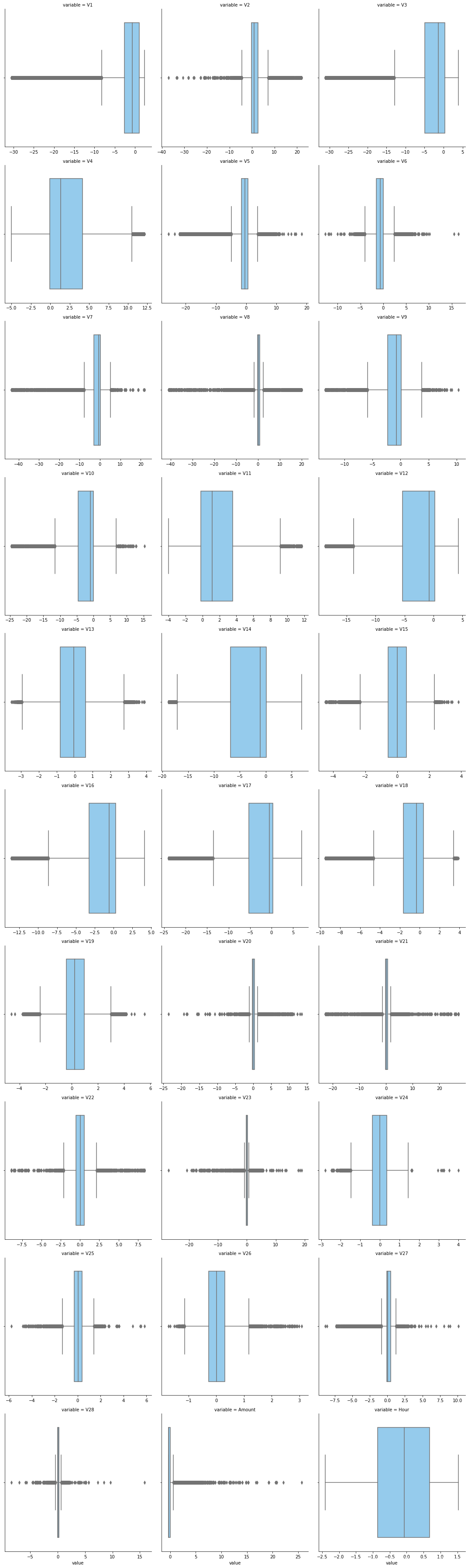
# 单个数值特征分布小提琴图
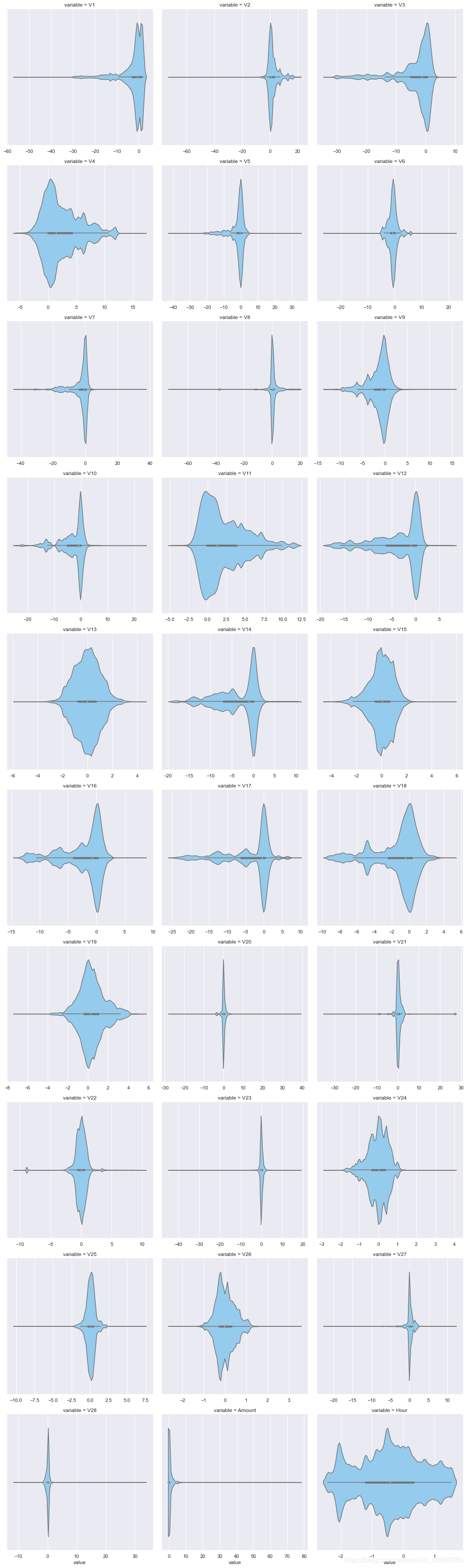
f = pd.melt(data_smote, value_vars=X_train.columns)
g = sns.FacetGrid(f, col='variable', col_wrap=3, sharex=False, sharey=False,size=5)
g = g.map(sns.violinplot, 'value',color='lightskyblue')
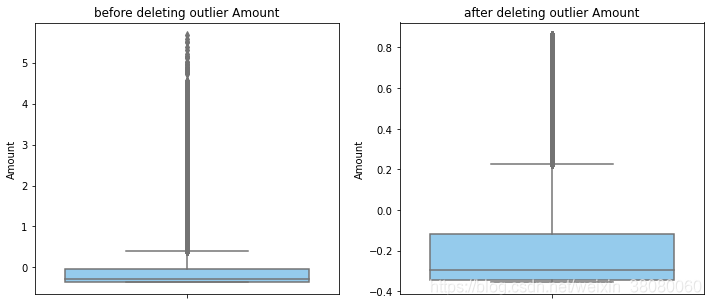
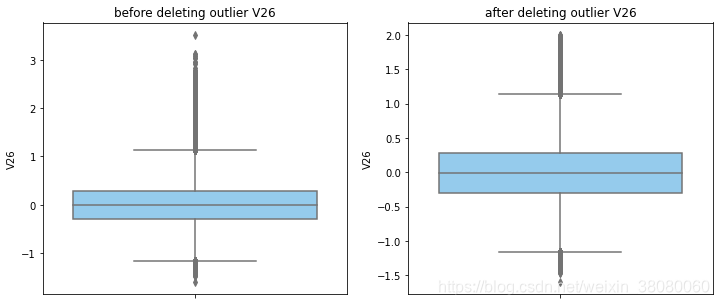
numerical_columns = data_smote.columns.drop('Class')
for col_name in numerical_columns:data_smote = outlier_process(data_smote,col_name)print(data_smote.shape)
(214362, 31)
(213002, 31)
(212497, 31)
(212497, 31)
(204320, 31)
(202425, 31)
(198165, 31)
(189719, 31)
(189492, 31)
(189427, 31)
(189020, 31)
(189019, 31)
(189019, 31)
(189019, 31)
(189016, 31)
(188944, 31)
(184836, 31)
(184556, 31)
(184552, 31)
(180426, 31)
(178559, 31)
(178559, 31)
(174526, 31)
(174457, 31)
(174354, 31)
(174098, 31)
(169488, 31)
(166755, 31)
(156423, 31)
(156423, 31)




#绘制采样前和采样后的热力图
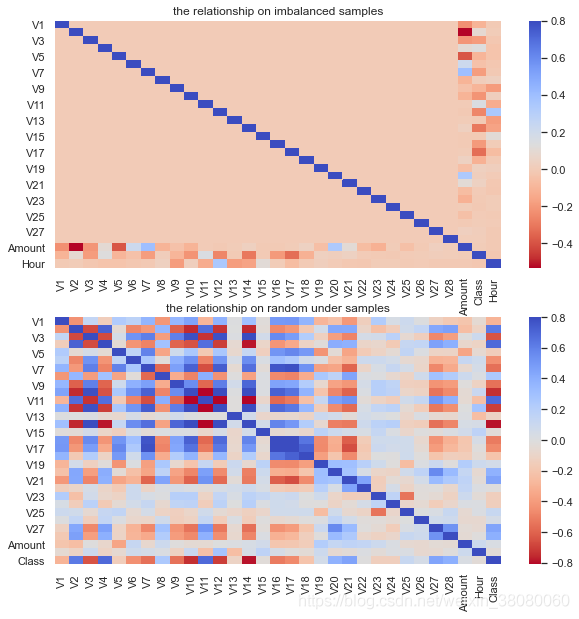
fig,(ax1,ax2) = plt.subplots(2,1,figsize=(10,10))
sns.heatmap(data.corr(),cmap = 'coolwarm_r',ax=ax1,vmax=0.8)
ax1.set_title('the relationship on imbalanced samples')
sns.heatmap(data_smote.corr(),cmap = 'coolwarm_r',ax=ax2,vmax=0.8)
ax2.set_title('the relationship on random under samples')
Text(0.5, 1.0, 'the relationship on random under samples')
# 分析数值属性与Class之间的相关性
data_smote.corr()['Class'].sort_values(ascending=False)
Class 1.000000
V11 0.713013
V4 0.705057
V2 0.641477
V21 0.466069
V27 0.459954
V28 0.383395
V20 0.381292
V8 0.253905
V25 0.147601
V26 0.052486
V19 0.008546
Amount -0.001365
V15 -0.023988
V22 -0.028250
Hour -0.048206
V5 -0.098754
V13 -0.142258
V24 -0.154369
V23 -0.157138
V18 -0.170994
V1 -0.295297
V17 -0.445826
V6 -0.465282
V16 -0.500016
V7 -0.547495
V9 -0.567131
V3 -0.658294
V12 -0.713942
V10 -0.748285
V14 -0.790148
Name: Class, dtype: float64
根据排名,和预测值Class正相关值较大的有V4,V11,V2,负相关值较大的有V_14,V_10,V_12,V_3,V7,V9,我们画出这些特征与预测值之间的关系图
# 正相关的属性与Class分布图
fig,(ax1,ax2,ax3) = plt.subplots(1,3,figsize=(24,6))
sns.violinplot(x='Class',y='V4',data=data_smote,palette=['lightsalmon','lightskyblue'],ax=ax1)
ax1.set_title('V11 vs Class Positive Correlation')sns.violinplot(x='Class',y='V11',data=data_smote,palette=['lightsalmon','lightskyblue'],ax=ax2)
ax2.set_title('V4 vs Class Positive Correlation')sns.violinplot(x='Class',y='V2',data=data_smote,palette=['lightsalmon','lightskyblue'],ax=ax3)
ax3.set_title('V2 vs Class Positive Correlation')
Text(0.5, 1.0, 'V2 vs Class Positive Correlation')

# 正相关的属性与Class分布图
fig,((ax1,ax2,ax3),(ax4,ax5,ax6)) = plt.subplots(2,3,figsize=(24,14))
sns.violinplot(x='Class',y='V14',data=data_smote,palette=['lightsalmon','lightskyblue'],ax=ax1)
ax1.set_title('V14 vs Class negative Correlation')sns.violinplot(x='Class',y='V10',data=data_smote,palette=['lightsalmon','lightskyblue'],ax=ax2)
ax2.set_title('V4 vs Class negative Correlation')sns.violinplot(x='Class',y='V12',data=data_smote,palette=['lightsalmon','lightskyblue'],ax=ax3)
ax3.set_title('V12 vs Class negative Correlation')sns.violinplot(x='Class',y='V3',data=data_smote,palette=['lightsalmon','lightskyblue'],ax=ax4)
ax4.set_title('V3 vs Class negative Correlation')sns.violinplot(x='Class',y='V7',data=data_smote,palette=['lightsalmon','lightskyblue'],ax=ax5)
ax5.set_title('V7 vs Class negative Correlation')sns.violinplot(x='Class',y='V9',data=data_smote,palette=['lightsalmon','lightskyblue'],ax=ax6)
ax6.set_title('V9 vs Class negative Correlation')Text(0.5, 1.0, 'V9 vs Class negative Correlation')
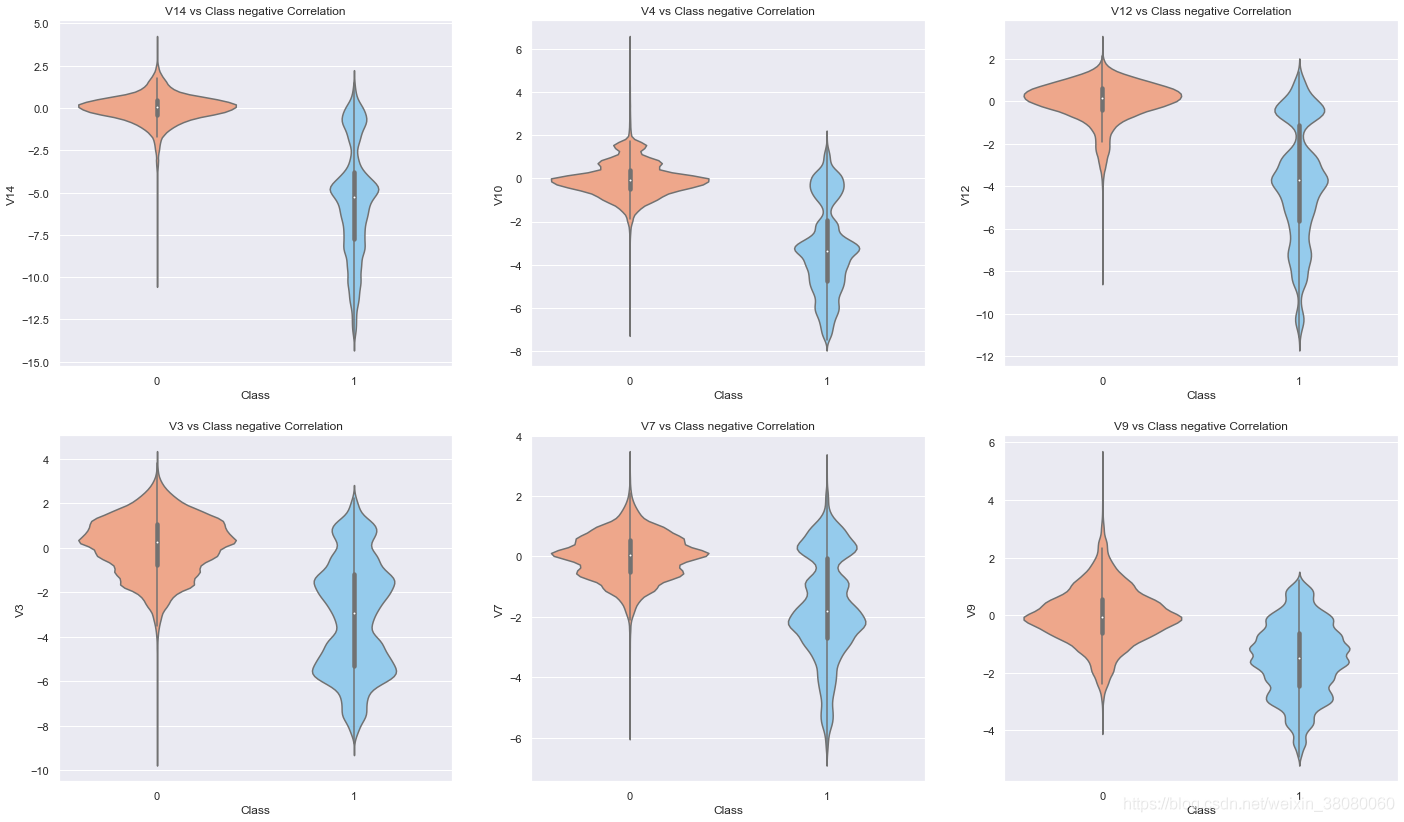
vif = [variance_inflation_factor(data_smote.values, data_smote.columns.get_loc(i)) for i in data_smote.columns]
vif
[8.91488639686892,41.95138589208644,29.439659166987383,9.321076032190051,18.073107065112527,7.88968653431388,38.13243240821064,2.61807436913295,4.202219415722627,20.898417802753006,5.976908659263689,10.856930462897152,1.2514060420970867,20.23958581764367,1.176425772463202,6.444784613229281,6.980222815257359,2.7742773520511372,2.4906782119059176,4.348667463801223,3.409678717638936,1.9626453781659197,2.1167419900555884,1.1352046295467655,1.9935984979230046,1.1029041559046275,3.084861887885401,1.9565486505075638,13.535498930988794,1.7451075607624895,4.64505815138509]
相较于随机下采样来说,在多重共线性上相对有了改善
# 利用Lasso进行特征选择
#调用LassoCV函数,并进行交叉验证
model_lasso = LassoCV(alphas=[0.1,0.01,0.005,1],random_state=1,cv=5).fit(X_smote,y_smote)
#输出看模型中最终选择的特征
coef = pd.Series(model_lasso.coef_,index=X_smote.columns)
print(coef[coef != 0])
V1 -0.019851
V2 0.004587
V3 0.000523
V4 0.052236
V5 -0.000597
V6 -0.012474
V7 0.030960
V8 -0.012043
V9 0.007895
V10 -0.023509
V11 0.005633
V12 0.009648
V13 -0.036565
V14 -0.053919
V15 0.012297
V17 -0.009149
V18 0.030941
V20 0.010266
V21 0.013880
V22 0.019031
V23 -0.009253
V26 -0.068311
V27 -0.003680
V28 0.008911
dtype: float64
# 利用随机森林进行特征重要性排序
from sklearn.ensemble import RandomForestClassifier
rfc_fea_model = RandomForestClassifier(random_state=1)
rfc_fea_model.fit(X_smote,y_smote)
fea = X_smote.columns
importance = rfc_fea_model.feature_importances_
a = pd.DataFrame()
a['feature'] = fea
a['importance'] = importance
a = a.sort_values('importance',ascending = False)
plt.figure(figsize=(20,10))
plt.bar(a['feature'],a['importance'])
plt.title('the importance orders sorted by random forest')
plt.show()

a.cumsum()
| feature | importance | |
|---|---|---|
| 13 | V14 | 0.140330 |
| 11 | V14V12 | 0.274028 |
| 9 | V14V12V10 | 0.392515 |
| 16 | V14V12V10V17 | 0.501863 |
| 3 | V14V12V10V17V4 | 0.592110 |
| 10 | V14V12V10V17V4V11 | 0.680300 |
| 1 | V14V12V10V17V4V11V2 | 0.728448 |
| 2 | V14V12V10V17V4V11V2V3 | 0.770334 |
| 15 | V14V12V10V17V4V11V2V3V16 | 0.808083 |
| 6 | V14V12V10V17V4V11V2V3V16V7 | 0.842341 |
| 17 | V14V12V10V17V4V11V2V3V16V7V18 | 0.857924 |
| 7 | V14V12V10V17V4V11V2V3V16V7V18V8 | 0.869777 |
| 20 | V14V12V10V17V4V11V2V3V16V7V18V8V21 | 0.880431 |
| 28 | V14V12V10V17V4V11V2V3V16V7V18V8V21Amount | 0.890861 |
| 0 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1 | 0.900571 |
| 8 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9 | 0.909978 |
| 12 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13 | 0.918623 |
| 18 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19 | 0.926978 |
| 26 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27 | 0.935072 |
| 4 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5 | 0.942688 |
| 29 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5Hour | 0.950275 |
| 19 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5HourV20 | 0.957287 |
| 14 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5HourV20V15 | 0.963873 |
| 5 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5HourV20V15V6 | 0.970225 |
| 25 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5HourV20V15V6V26 | 0.976519 |
| 27 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5HourV20V15V6V26V28 | 0.982202 |
| 22 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5HourV20V15V6V26V28V23 | 0.987770 |
| 21 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5HourV20V15V6V26V28V23V22 | 0.992335 |
| 24 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5HourV20V15V6V26V28V23V22V25 | 0.996295 |
| 23 | V14V12V10V17V4V11V2V3V16V7V18V8V21AmountV1V9V13V19V27V5HourV20V15V6V26V28V23V22V25V24 | 1.000000 |
从以上结果来看,两种方法的排序,特征重要性差别很大,为了更大程度的保留数据的信息,我们采用两种结合的特征,其中选择的标准是随机森林中重要性总和95%以上,如果其中有Lasso回归没有的,则加入,共选出除去V24,V25之外的28个特征
# test_cols = ['V12', 'V14', 'V10', 'V17', 'V4', 'V11', 'V2', 'V7', 'V16', 'V3', 'V18',
# 'V8', 'Amount', 'V19', 'V21', 'V1', 'V5', 'V13', 'V27','V6','V15','V26']
test_cols = X_smote.columns.drop(['V24','V25'])
Classifiers = {'LG': LogisticRegression(random_state=1),'KNN': KNeighborsClassifier(),'Bayes': GaussianNB(),'SVC': SVC(random_state=1, probability=True),'DecisionTree': DecisionTreeClassifier(random_state=1),'RandomForest': RandomForestClassifier(random_state=1),'Adaboost': AdaBoostClassifier(random_state=1),'GBDT': GradientBoostingClassifier(random_state=1),'XGboost': XGBClassifier(random_state=1),'LightGBM': LGBMClassifier(random_state=1)
}
Y_pred, Accuracy_score = train_test(Classifiers, X_smote[test_cols], y_smote, X_test[test_cols], y_test)
print(Accuracy_score)
Y_pred.head()
LGprecision recall f1-score support0 1.00 0.98 0.99 568631 0.06 0.86 0.12 98accuracy 0.98 56961macro avg 0.53 0.92 0.55 56961
weighted avg 1.00 0.98 0.99 56961KNNprecision recall f1-score support0 1.00 1.00 1.00 568631 0.29 0.83 0.42 98accuracy 1.00 56961macro avg 0.64 0.91 0.71 56961
weighted avg 1.00 1.00 1.00 56961Bayesprecision recall f1-score support0 1.00 0.98 0.99 568631 0.06 0.84 0.11 98accuracy 0.98 56961macro avg 0.53 0.91 0.55 56961
weighted avg 1.00 0.98 0.99 56961SVCprecision recall f1-score support0 1.00 0.99 0.99 568631 0.09 0.86 0.17 98accuracy 0.99 56961macro avg 0.55 0.92 0.58 56961
weighted avg 1.00 0.99 0.99 56961DecisionTreeprecision recall f1-score support0 1.00 1.00 1.00 568631 0.27 0.80 0.40 98accuracy 1.00 56961macro avg 0.63 0.90 0.70 56961
weighted avg 1.00 1.00 1.00 56961RandomForestprecision recall f1-score support0 1.00 1.00 1.00 568631 0.81 0.82 0.81 98accuracy 1.00 56961macro avg 0.90 0.91 0.91 56961
weighted avg 1.00 1.00 1.00 56961Adaboostprecision recall f1-score support0 1.00 0.98 0.99 568631 0.06 0.89 0.12 98accuracy 0.98 56961macro avg 0.53 0.93 0.55 56961
weighted avg 1.00 0.98 0.99 56961GBDTprecision recall f1-score support0 1.00 0.99 0.99 568631 0.13 0.85 0.22 98accuracy 0.99 56961macro avg 0.56 0.92 0.61 56961
weighted avg 1.00 0.99 0.99 56961[15:24:00] WARNING: C:/Users/Administrator/workspace/xgboost-win64_release_1.4.0/src/learner.cc:1095: Starting in XGBoost 1.3.0, the default evaluation metric used with the objective 'binary:logistic' was changed from 'error' to 'logloss'. Explicitly set eval_metric if you'd like to restore the old behavior.
XGboostprecision recall f1-score support0 1.00 1.00 1.00 568631 0.69 0.84 0.76 98accuracy 1.00 56961macro avg 0.84 0.92 0.88 56961
weighted avg 1.00 1.00 1.00 56961LightGBMprecision recall f1-score support0 1.00 1.00 1.00 568631 0.54 0.83 0.66 98accuracy 1.00 56961macro avg 0.77 0.91 0.83 56961
weighted avg 1.00 1.00 1.00 56961LG KNN Bayes SVC DecisionTree RandomForest Adaboost GBDT XGboost LightGBM
0 0.977862 0.996138 0.976335 0.985113 0.995874 0.99935 0.977054 0.9898 0.99907 0.998508
| LG | KNN | Bayes | SVC | DecisionTree | RandomForest | Adaboost | GBDT | XGboost | LightGBM | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
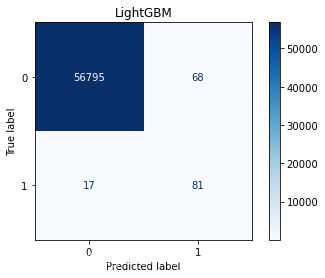

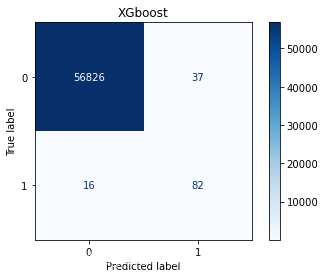
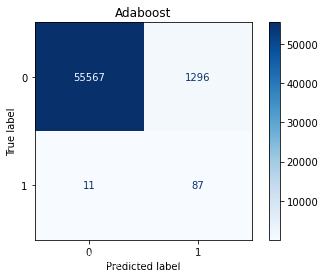

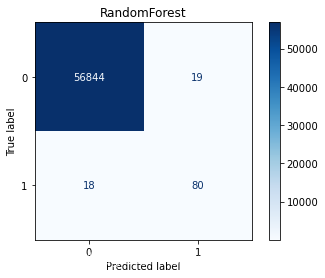
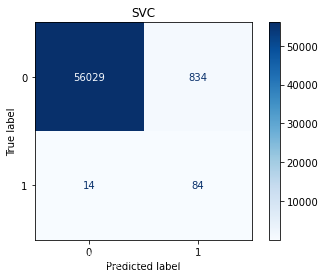
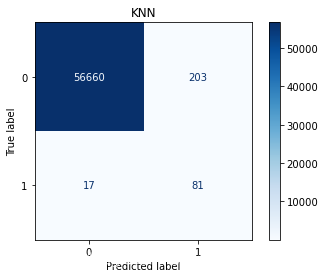
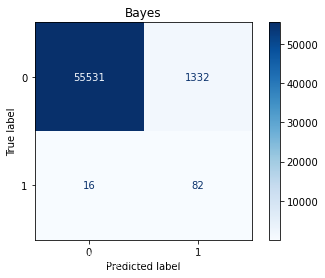
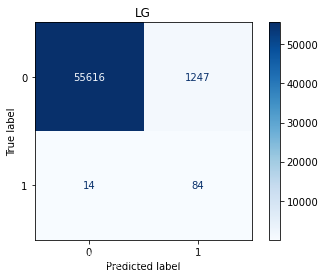
从精确度上可以看出,经过了SMOTE上采样和随机下采样之后,精确度有了很好的提升,比如随机森林RandomForest达到了99.94%的精确度,在样本数量上分别是13个欺诈样本的没有识别,误将18个非欺诈样本识别为欺诈样本,其他的算法如XGBoost,lightGBM,KNN等都达到了99%的准确率,下面使用准确率高的模型进行集成
因为样本量较大,而参数调优也比较耗时,目前的效果也比较好,因而省略网格调优的过程,时间足够的可以像前面一样调优。
Classifiers = {'LG': reg_best(X_smote[test_cols], y_smote),'KNN': KNN_best(X_smote[test_cols], y_smote),'Bayes': GaussianNB(),'SVC': SVC_best(X_smote[test_cols], y_smote),'DecisionTree': DecisionTree_best(X_smote[test_cols], y_smote),'RandomForest': RandomForest_best(X_smote[test_cols], y_smote),'Adaboost':Adaboost_best(X_smote[test_cols], y_smote),'GBDT': GBDT_best(X_smote[test_cols], y_smote),'XGboost': XGboost_best(X_smote[test_cols], y_smote),'LightGBM': LGBM_best(X_smote[test_cols], y_smote)}
LogisticRegression(C=1)
KNeighborsClassifier(n_neighbors=3)
SVC(C=1, probability=True)
DecisionTreeClassifier(max_depth=3, min_samples_leaf=5)
RandomForestClassifier(criterion='entropy', min_samples_leaf=5)
AdaBoostClassifier(learning_rate=1, n_estimators=200)
GradientBoostingClassifier(n_estimators=150)
XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,colsample_bynode=1, colsample_bytree=1, gamma=0, gpu_id=-1,importance_type='gain', interaction_constraints='',learning_rate=0.5, max_delta_step=0, max_depth=5,min_child_weight=1, missing=nan, monotone_constraints='()',n_estimators=200, n_jobs=8, num_parallel_tree=1, random_state=0,reg_alpha=0, reg_lambda=1, scale_pos_weight=1, subsample=1,tree_method='exact', validate_parameters=1, verbosity=None)
LGBMClassifier(learning_rate=0.5, max_depth=15, num_leaves=51)
Y_pred,Accuracy_score = train_test(Classifiers, X_smote[test_cols], y_smote, X_test[test_cols], y_test)
print(Accuracy_score)
Y_pred.head().append(Y_pred.tail())
LGprecision recall f1-score support0 1.00 0.97 0.99 568631 0.06 0.91 0.11 98accuracy 0.97 56961macro avg 0.53 0.94 0.55 56961
weighted avg 1.00 0.97 0.99 56961KNNprecision recall f1-score support0 1.00 0.98 0.99 568631 0.09 0.92 0.17 98accuracy 0.98 56961macro avg 0.55 0.95 0.58 56961
weighted avg 1.00 0.98 0.99 56961Bayesprecision recall f1-score support0 1.00 0.98 0.99 568631 0.07 0.88 0.12 98accuracy 0.98 56961macro avg 0.53 0.93 0.56 56961
weighted avg 1.00 0.98 0.99 56961SVCprecision recall f1-score support0 1.00 0.98 0.99 568631 0.08 0.90 0.15 98accuracy 0.98 56961macro avg 0.54 0.94 0.57 56961
weighted avg 1.00 0.98 0.99 56961DecisionTreeprecision recall f1-score support0 1.00 0.96 0.98 568631 0.04 0.90 0.08 98accuracy 0.96 56961macro avg 0.52 0.93 0.53 56961
weighted avg 1.00 0.96 0.98 56961RandomForestprecision recall f1-score support0 1.00 1.00 1.00 568631 0.33 0.90 0.48 98accuracy 1.00 56961macro avg 0.66 0.95 0.74 56961
weighted avg 1.00 1.00 1.00 56961Adaboostprecision recall f1-score support0 1.00 0.98 0.99 568631 0.08 0.90 0.15 98accuracy 0.98 56961macro avg 0.54 0.94 0.57 56961
weighted avg 1.00 0.98 0.99 56961GBDTprecision recall f1-score support0 1.00 0.99 0.99 568631 0.11 0.89 0.19 98accuracy 0.99 56961macro avg 0.55 0.94 0.59 56961
weighted avg 1.00 0.99 0.99 56961[17:58:32] WARNING: C:/Users/Administrator/workspace/xgboost-win64_release_1.4.0/src/learner.cc:1095: Starting in XGBoost 1.3.0, the default evaluation metric used with the objective 'binary:logistic' was changed from 'error' to 'logloss'. Explicitly set eval_metric if you'd like to restore the old behavior.
XGboostprecision recall f1-score support0 1.00 1.00 1.00 568631 0.24 0.90 0.38 98accuracy 0.99 56961macro avg 0.62 0.95 0.69 56961
weighted avg 1.00 0.99 1.00 56961LightGBMprecision recall f1-score support0 1.00 1.00 1.00 568631 0.30 0.90 0.45 98accuracy 1.00 56961macro avg 0.65 0.95 0.72 56961
weighted avg 1.00 1.00 1.00 56961LG KNN Bayes SVC DecisionTree RandomForest Adaboost GBDT XGboost LightGBM
0 0.97393 0.984463 0.978477 0.982936 0.963273 0.996629 0.982093 0.987026 0.994944 0.996208
| LG | KNN | Bayes | SVC | DecisionTree | RandomForest | Adaboost | GBDT | XGboost | LightGBM | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 56956 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 56957 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 56958 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 56959 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 56960 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
# 集成学习
# 根据以上auc以及recall的结果,选择LG,DT以及GBDT当作基模型
from sklearn.ensemble import VotingClassifier
voting_clf = VotingClassifier(estimators=[
# ('LG', LogisticRegression(random_state=1)),('KNN', KNeighborsClassifier(n_neighbors=3)),
# ('Bayes',GaussianNB()),
# ('SVC', SVC(random_state=1,probability=True)),('DecisionTree', DecisionTreeClassifier(random_state=1)),('RandomForest', RandomForestClassifier(random_state=1)),
# ('Adaboost',AdaBoostClassifier(random_state=1)),
# ('GBDT', GradientBoostingClassifier(random_state=1)),('XGboost', XGBClassifier(random_state=1)),('LightGBM', LGBMClassifier(random_state=1))])
voting_clf.fit(X_smote[test_cols], y_smote)
y_final_pred = voting_clf.predict(X_test[test_cols])
print(classification_report(y_test, y_final_pred))
fig, ax = plt.subplots(1, 1)
plot_confusion_matrix(voting_clf, X_test[test_cols], y_test, labels=[0, 1], cmap='Blues', ax=ax)
precision recall f1-score support0 1.00 1.00 1.00 568631 0.71 0.83 0.76 98accuracy 1.00 56961macro avg 0.86 0.91 0.88 56961
weighted avg 1.00 1.00 1.00 56961<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x1fe3047f3a0>
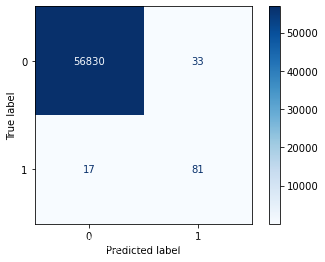
最终,根据我们选择的模型,能达到几乎100%的准确率,欺诈样本中有17个没有识别出,而在非欺诈样本中只有33个被识别为存在信用卡欺诈,与随机下采样在准确率上有了极大提升。在欺诈样本的识别上还有提升空间!