信用卡交易数据异常检测

一、案例背景以及数据集

二、代码

1、导入库，导入数据集。

2、数据标准化

3、下采样

4、划分训练集、测试集

5、建立模型，交叉验证

6、原始训练集预测效果

7、下采样训练集预测效果

8、绘制混淆矩阵

9、predict_proba自定义阈值

10、SMOTE

11、使用SVM分类

三、总结

一、案例背景以及数据集

信用卡欺诈是指以非法占有为目的，故意使用伪造、作废的信用卡，冒用他人的信用卡骗取财物，或用本人信用卡进行恶意透支的行为。

数据集“creditcard.csv”中的数据来自2013年9月由欧洲持卡人通过信用卡进行的交易。共284807行交易记录，其中数据文件中Class==1表示该条记录是欺诈行为，总共有 492 笔。输入数据中存在 28 个特征 V1，V2，……V28(通过PCA变换得到，不用知道其具体含义)，以及交易时间 Time 和交易金额 Amount。

百度云链接：https://pan.baidu.com/s/1_GLiEEqIZqXVG7M1lcnewg
提取码：abcd

目标：构建一个信用卡欺诈分析的分类器。通过以往的交易数据分析出每笔交易是否正常，是否存在盗刷风险。

二、代码

1、导入库，导入数据集。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as npdata = pd.read_csv("creditcard.csv")
data.head()
pd.value_counts(data['Class'], sort = True)

从运行结果可以看出，正常记录有284315条，而欺诈行为记录只有492条，后者占总数的0.2%不到，说明样本数据极度不均衡。也就是说，只要生成一个永远把样本预测为反例的分类器，准确率就可以达到99.8%了，可是这样的分类器没有丝毫意义，因为它不能预测出任何正例。

那么如何解决数据类别不平衡问题呢？就是要让标签值(如0和1分类)中的样本数据量大致相同。

常用的方法有：

(1)、过采样(oversampling the minority)。即以数据量多的一方的样本数量为标准，把样本数量较少的类的样本数量生成和样本数量多的一方相同。SMOTE也是一种过采样方法，其基本思想是对少数类样本进行分析，并根据少数类样本人工合成新样本添加到数据集中。即以每个少数类样本点的k个最近邻样本点为依据，随机的选择N个邻近点进行差值并乘上一个[0,1]范围的随机因子，从而达到合成数据的目的。(两种样本数量一样多)

(2)、欠采样(under-sampling the majority)。即以数据量少的一方的样本数量为准，从分类样本多的数据从随机抽取等量的样本。(两种样本数量一样少)

2、数据标准化

可以观察特征V28的数值浮动较小。而特征Amount的值分布差异较大，如果不经处理直接拿来训练，学习系统会认为Amount的值越大，其重要程度就越大。为消除数据特征之间的量纲影响，使得各特征重要程度相当，就要对数据进行标准化处理。

数据标准化（Normalization），即将数据值缩放成均值为0，方差为1的状态。

$x'=\frac{x-\mu }{\sigma }$

$\mu$ 和 $\sigma$ 分别是样本数据的均值(mean)和标准差(std)。

from sklearn.preprocessing import StandardScaler #标准化模块data['normAmount'] = StandardScaler().fit_transform(data.Amount.values.reshape(-1, 1))  
data = data.drop(['Time','Amount'],axis=1)  #删除不需要的列
data.head()

3、下采样

即使得Class列中，值为0、1的数据量一样少。

X = data.iloc[:, data.columns != 'Class'] #特征数据
y = data.iloc[:, data.columns == 'Class'] #标签数据number_records_fraud = len(data[data.Class == 1])     #异常样本数量
fraud_indices = data[data.Class == 1].index           #得到所有异常样本的索引
normal_indices = data[data.Class == 0].index          #得到所有正常样本的索引# 在正常样本中随机采样
random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace = False)# 根据索引得到下采样所有样本
under_sample_data = data.iloc[np.concatenate([fraud_indices,random_normal_indices]),:]
X_undersample = under_sample_data.iloc[:, under_sample_data.columns != 'Class']  #特征数据
y_undersample = under_sample_data.iloc[:, under_sample_data.columns == 'Class']  #标签数据pd.value_counts(under_sample_data['Class'], sort = True) #观察数据

最终从284315条正常样本中取出492条样本数据，下采样的缺点是对样本数据利用率低，大多数数据并没有被用到。

4、划分训练集、测试集

利用train_test_split函数随机的将样本数据分为两部分。然后用训练集来训练模型，在测试集上验证模型及参数。参数test_size设为0.3表示分成70%的训练集，30%的测试集。参数random_state设置为0表示每次随机划分的结果都是一样的，可以控制数据避免产生不必要的变化。

from sklearn.model_selection import train_test_split# 对原始数据集进行划分
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3, random_state = 0)
len(X_train)  #原始训练集包含样本数量
len(X_test)   #原始测试集包含样本数量# 对下采样数据集进行划分
X_train_undersample, X_test_undersample, y_train_undersample, y_test_undersample = train_test_split(X_undersample,y_undersample,test_size = 0.3,random_state = 0)
len(X_train_undersample)  #下采样训练集包含样本数量
len(X_test_undersample)   #下采样测试集包含样本数量

5、建立模型，交叉验证

逻辑回归模型是机器学习中最常用最经典的分类方法之一，常用于处理分类问题。在这里使用逻辑回归模型来训练，最终通过sigmoid函数得到一个概率值，大于0.5就说明风险较高，判定是正例。小于0.5，就说明是欺诈行为的可能性较低。

L1正则化可以看做是损失函数的惩罚项，可产生稀疏权值矩阵，即产生一个稀疏模型用于特征选择（在这个项目中有29个特征，可是各特征对模型的贡献度是不一样的，有的特征贡献大，有的特征贡献小）。

带L1正则化项的损失函数就是在原来的损失函数基础上加上权重参数的绝对值： $\alpha \cdot \sum_{w}^{}|w|$ 。其中，α是正则化系数，通过控制α来调整惩罚力度，在本项目中取为0.01。

在前面有说过本项目由于样本数据不均衡，故而用准确率(Accuracy)来评估模型不太妥善，所以选择用召回率(Recall)来评估模型：

$Recall=\frac{TP}{TP+FN}$

其中，TP(True Positives)表示：正例样本通过模型被判定为正例。FN(False Negatives)表示：正例样本通过模型被判定为负例。

而准确率是正例样本被判定为正例，负例样本被判定为负例，占总体样本的比例。

若将样本数据简单划分为训练集和测试集。测试集是与训练独立的数据，只被用于最终模型的评估。如此评估模型时，经常会出现过拟合的问题，即模型在训练数据上表现好，却在测试数据上表现差。所以通常在训练数据中分出一部分做为验证数据，用来评估模型的训练效果。验证数据取自训练数据，但不参与训练，就可以相对客观的评估模型对于训练集之外数据的预测效果。

在此处使用K折交叉验证，取K=5，即将训练集分成5份，每个子集数据依次成为验证集，同时其余4组子集数据作为训练集。这样一共要循环5次，验证5次，并得到5个模型，对其误差计算均值，即得到交叉验证误差。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold
from sklearn.metrics import confusion_matrix,recall_scoredef printing_Kfold_scores(x_train_data,y_train_data):# k-fold表示K折的交叉验证，会得到两个索引集合: 训练集 = indices[0], 验证集 = indices[1]fold = KFold(5,shuffle=False) recall_accs = []for iteration, indices in enumerate(fold.split(x_train_data)): # 实例化算法模型，指定l1正则化lr = LogisticRegression(C = 0.01, penalty = 'l1',solver='liblinear')# 训练模型，传入的是训练集，所以X和Y的索引都是0lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())# 建模后，预测模型结果，这里用的是验证集，索引为1y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)# 评估召回率，需要传入真实值和预测值recall_acc = round(recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample),4)recall_accs.append(recall_acc)print('第', iteration+1,'次迭代：召回率 = ', recall_acc)# 当执行完交叉验证后，计算平均结果print('平均召回率 ', round(np.mean(recall_accs),4))return None

6、原始训练集预测效果

printing_Kfold_scores(X_train,y_train)

输出结果：
第 1 次迭代：召回率 =  0.4925
第 2 次迭代：召回率 =  0.6027
第 3 次迭代：召回率 =  0.6833
第 4 次迭代：召回率 =  0.5692
第 5 次迭代：召回率 =  0.45
平均召回率  0.5595

可以看出，在原始训练集上，并没有能很好地预测出正例。

7、下采样训练集预测效果

printing_Kfold_scores(X_train_undersample,y_train_undersample)

输出结果：

第 1 次迭代：召回率 =  0.9589
第 2 次迭代：召回率 =  0.9452
第 3 次迭代：召回率 =  1.0
第 4 次迭代：召回率 =  0.973
第 5 次迭代：召回率 =  0.9697
平均召回率  0.9694

可以看出，在下采样训练集上，对于正例的预测效果比较不错。

8、绘制混淆矩阵

混淆矩阵（confusion matrix），又称为可能性表格或是错误矩阵。它是一种用来可视化呈现算法性能的特定矩阵，每一列代表预测值，每一行代表的是实际的类别即真实值。

混淆矩阵
Predicted label True label	0	1
0	True Negatives(TN，真实反例被预测为反例)	False Positives(FP，真实反例被预测为正例，即“存伪”)
1	False Negatives(FN，真实正例被预测为反例，即“去真”)	True Positives(TP，真实正例被预测为正例)

import itertoolsdef plot_confusion_matrix(cm, classes,title='Confusion matrix',cmap=plt.cm.Blues):plt.imshow(cm, interpolation='nearest', cmap=cmap)plt.title(title)plt.colorbar()tick_marks = np.arange(len(classes))plt.xticks(tick_marks, classes, rotation=0)plt.yticks(tick_marks, classes)thresh = cm.max() / 2.for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):plt.text(j, i, cm[i, j],horizontalalignment="center",color="white" if cm[i, j] > thresh else "black")plt.tight_layout()plt.ylabel('True label')plt.xlabel('Predicted label')#下采样训练集训练之后，预测原始测试集
lr = LogisticRegression(C = 0.01, penalty = 'l1',solver='liblinear')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred = lr.predict(X_test.values)
print("召回率: ", recall_score(y_test.values, y_pred))# 绘制混淆矩阵
plot_confusion_matrix(confusion_matrix(y_test,y_pred) ,[0,1])

从绘制的混淆矩阵可以看出FP的数量过大，存在很多“误伤”的现象，即将10357条正常数据判定成了欺诈行为。准确率不高，Recall值却还不错。

9、predict_proba自定义阈值

为缓解上面“误伤”的现象，可以自定义判定概率阈值。即使得对异常数据的判定更“严格”一些。使用predict()函数预测时，最终分类的概率大于0.5即被认为是欺诈行为。可以使用predict_proba()函数来自定义一个阈值，如0.6。随着阈值增大，召回率会越低。

y_pred_proba = lr.predict_proba(X_test.values)
y_classify = y_pred_proba[:,1] > 0.6print("召回率: ", recall_score(y_test.values, y_classify))
plot_confusion_matrix(confusion_matrix(y_test,y_classify), [0,1])

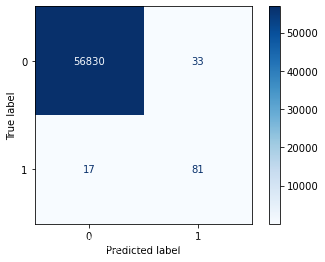
可以看出，在阈值设定为0.6时，召回率和准确率都还不错。

10、SMOTE

使用SMOTE算法将训练集中异常数据生成到与正常数据一样多，从345变为199019条，从而解决样本数据不均衡问题。

from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifieroversampler=SMOTE(random_state=0)
os_data,os_labels=oversampler.fit_resample(X_train,y_train)
pd.value_counts(os_labels.Class)lr = LogisticRegression(C = 0.01, penalty = 'l1',solver='liblinear')
lr.fit(os_data,os_labels.values.ravel())
os_pred = lr.predict(X_test.values)print("召回率: ", recall_score(y_test.values, os_pred))
plot_confusion_matrix(confusion_matrix(y_test,os_pred) ,[0,1])

可以看出，使用SMOTE算法过采样要比下采样的效果更好一些。

11、使用SVM分类

from sklearn import svm
s=svm.SVC(kernel='linear')
s.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_svm=s.predict(X_test.values)
print("召回率: ", recall_score(y_test.values, y_pred_svm))
plot_confusion_matrix(confusion_matrix(y_test,y_pred_svm) ,[0,1])