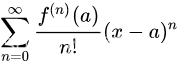2022考研笔记-数学(高等数学预备知识)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/72384.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
汤家凤高等数学基础手写笔记-导数与微分
越来越发现,下层基础决定上层建筑。除了考试,在研究中,我们能够用到的就是理论体系的知识,而不是会做题目的多少。做题目的目的在于加深对基础理论的理解。
本系列笔记汇总之处:汤家凤高等数学基础课2020年基础笔记概…
【高数】高数竞赛必背重点(随时更)
高数竞赛必背重点(随时更) 博主高数相关文章链接 左边为必背知识点,右边为备注栏 博主高数相关文章链接
高数第一章节——极限&无穷&连续与间断 高数第二章节——导数&求导法则&高阶导数&微分 高数第三章节——微分中值…
高等数学辅导讲义_历年真题,复习讲义的经验分享(数二127分)
纯属个人经验 之前的回答里面提到了我使用的教材 2021 考研数学该怎么复习?www.zhihu.com 其实我刚开始备考的时候,也跟很多人一样,盲目的买了很多教材,又买了很多练习册,刚开始备考的时候看着一大摞书,心里就开始飘了,想着做完这些拿高分还不是轻轻松松 然而现实很残…
高数————思维导图(上岸必备)(积分部分)
高数————思维导图(上岸必备)(极限与连续).
高数————思维导图(上岸必备)(微分部分).
高数————思维导图(上岸必备)(积分部分).
高数————思维导图(上岸必备)(级数部…
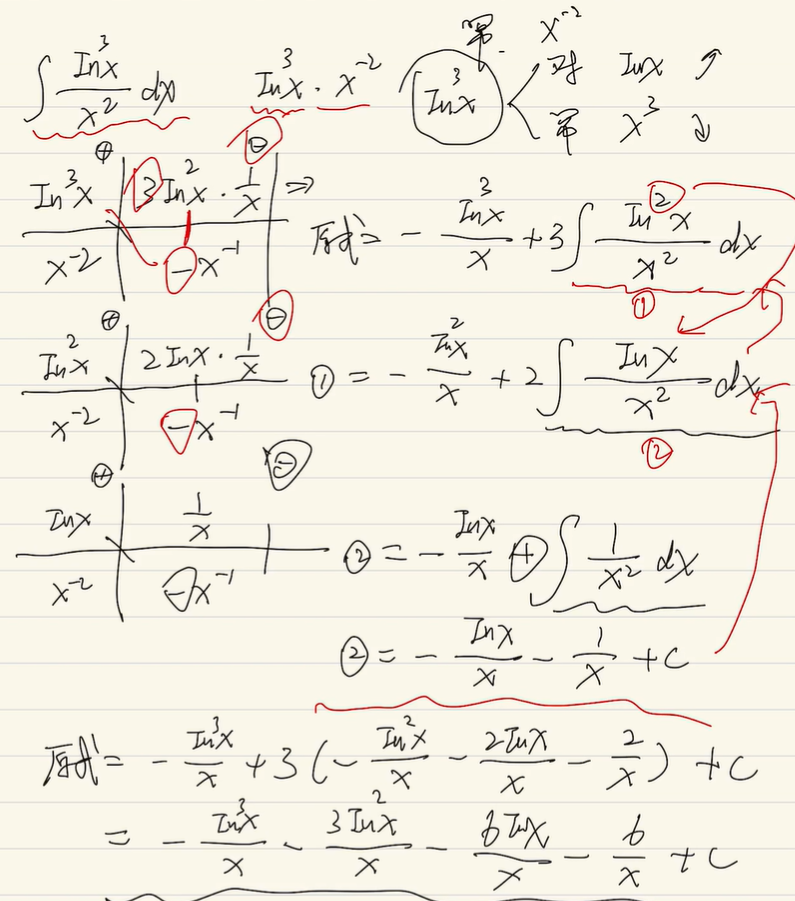
2022张宇考研基础30讲 第八讲 一元函数积分学的概念与计算
文章目录 第八讲 一元函数积分学的概念与计算不定积分原函数(不定积分)存在定理用导数介值定理解释 定积分变限积分不定积分与变限积分的比较 积分的奇偶性积分的周期性反常积分基本积分公式基本积分方法凑微分法换元法分部积分法: 有理函数的…
2022mathorcupD题思路交流
今年Mathorcup难度整体难度比较大,四道题对算法编程能力要求都较高,计算量都比较大。作为新手的话建议可以优先考虑A和D题,整体对新手稍微友好一些。这里给出D题我的思路,仅供大家参考。移动通信网络站址规划和区域聚类问题&#…
高等数学辅导讲义严选题辅导讲义(学习笔记)
第一章 函数 极限 连续(选择题部分): 问题描述 问题分析: 思路:判断ABC三个选项比较复杂,D选项易于判断 解决方法: 问题描述 问题分析: 定理:若f(x࿰…
【考研笔记】数学一 · 高等数学笔记
考研一战顺利上岸啦,报考专业计算机科学与技术,考的数一英一。现在离开学还有段时间,所以趁机把自己的笔记都整理一下,希望可以帮到一些备考的同学。
写在前面:
首先说一下自己的复习计划跟想法。数一今年有点难&am…
全国大学生数学竞赛备考——高数上(极限、导数、微分、积分、级数)
我真的会忘(3) 极限两个重要极限公式常用极限公式 导数、微分与积分牛顿-莱布尼茨公式莱布尼兹公式微分中值定理罗马中值定理拉格朗日中值定理柯西定理 泰勒公式几个常见的麦克劳林公式 洛必达曲率曲率圆牛顿迭代法积分中值定理分部积分法 级数正项级数审…
考研数学刷题知能行怎么样?
被考研数学折磨的小伙伴看过来!
恭喜你,捡到宝了!本人22考研数二选手,人在宿舍,刚下考场。本人从高中开始数学就一直很拉胯,学数学对我来说真的是太折磨了QAQ 从1月份开始准备考研数学,一开始真…
知能行考研数学的高数部分怎么样?大一可以用吗?
目录
方法一等价替换
方法二泰勒公式
方法三洛必达法则
一、值得一看的网课
二、带着问题听课
三、如何调整在学习高数时的心态
四、总结 我上大学的时候,面对这两部分知识点,也学得很吃力,尤其是微积分
但是后来我学明白之后&#x…
迭代后首波实测!360智脑一键联网,代码超强,AI诈骗一眼看穿
360大模型(又)交卷了!作为国内首个能联网的大模型,360智脑给了我们怎样的惊喜?话不多说,新鲜出炉的第一手实测来了。 不得不说,自从GPT大模型混战开赛之后,教主周鸿祎可谓是存在感十…
AI公司CEO冒充中科大少年班校友!清华、斯坦福名校经历全造假
点击下方卡片,关注“CVer”公众号 AI/CV重磅干货,第一时间送达 转自:3D实验室 | 来源:中国科大新创校友基金会 打假 中国科学技术大学新创校友基金会与中国科学技术大学少年班校友会(以下分别简称“中国科大新创校友…
斯坦福前校长John Hennessy、张亚勤等一众大佬云集,共探最前沿技术 | CNCC2020
金磊 发自 凹非寺量子位 报道 | 公众号 QbitAI 基础软件、尖端技术,频频被「卡脖子」,当下时局该如何突围? 这或许就是当下技术从业者,最为关心的一个问题。 由中国计算机学会 (CCF)举办的中国计算机大会 &…
ChatGPT - 使用28原则快速学习的Prompt
文章目录 Prompt例子 Prompt
“我想了解[你想了解的主题]。识别并分享该主题中最重要的20%的学习内容,这将帮助我理解80%的内容。”例子
挖掘GPT的隐藏实力就靠它了
克雷西 发自 凹非寺量子位 | 公众号 QbitAI 这个GitHub新项目,能让ChatGPT完成复杂任务,GPT3.5和GPT-4都支持。 它通过将问题拆解,并调用外部资源,提高了GPT的工作能力。 在它的调教下,GPT-4回答的准确率从68%提高到了…
文心一言和讯飞星火全面对比测试:(三)常识问题
前文回顾:
在(一)语言理解能力测试中,我们主要测试了两个大语言模型对复杂语义的理解、对文章情绪的识别、对文章进行摘要总结、对文章进行要素提取,测试结果表明:在语言理解能力上:除了有些问…
文心一言:垂直深度体验
3月19号,我发布了百度文心一言和ChatGPT的对比测试。
紧接着,3月20号,百度文心一言就推出了v1.0.1新版本。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kpLCnihL-1679462810728)(http://oss-qiniu.kujiajia.x…
最新文章
- 天津网站建立/杭州网站优化效果
- 设计图片大全 效果图/临沂seo全网营销
- 免费空间+网站空间+虚拟主机/网站宣传
- 郑州做网站熊掌号/电商平台排行榜前十名
- 学习网站建设/脚本外链生成工具
- 怎么用百度云做网站空间/b2b电商平台
- C#语言详解:从基础到进阶
- C/C++语言基础--C++模板与元编程系列六,C++元编程相关库的讲解与使用
- Shell 脚本中的大小写陷阱:为什么 ${PWD} 而不是 ${pwd}?
- uni-app之数据驱动的picker选择器( uni-data-picker)之可以选择到任意级别
- 探索 HTML 和 CSS 实现的蜡烛火焰
- 动态规划问题-删除并获得点数(Java实现)
推荐文章
- 7.3 项目3 贪吃蛇(控制台版) (A)
- 软考-高级-信息系统项目管理师教程 第四版【第19章-配置与变更管理-思维导图】
- ##15 探索高级数据增强技术以提高模型泛化能力
- (11)(2.1.2) DShot ESCs(二)
- (2)(2.11) RFD900
- (24)(24.1) FPV和仿真的机载OSD(三)
- (52)MATLAB仿真说明迫零均衡器的缺点
- (aiohttp-asyncio-FFmpeg-Docker-SRS)实现异步摄像头转码服务器
- (SSO单点登录)多个系统之间如何实现账号互通
- (二)延时任务篇——通过redis的key监听,实现延迟任务实战
- (计算机网络)网络层
- (每日持续更新)jdk api之SequenceInputStream基础、应用、实战