25.9 matlab里面的10中优化方法介绍—— 惩罚函数法求约束最优化问题（matlab程序）

1.简述

一、算法原理
1、问题引入
之前我们了解过的算法大部分都是无约束优化问题，其算法有：黄金分割法，牛顿法，拟牛顿法，共轭梯度法，单纯性法等。但在实际工程问题中，大多数优化问题都属于有约束优化问题。惩罚函数法就可以将约束优化问题转化为无约束优化问题，从而使用无约束优化算法。

2、约束优化问题的分类
约束优化问题大致分为三类：等式约束、不等式约束、等式+不等式约束。

其数学模型为：

等式约束

s.t hv(x)=0,v=1,2,...,p<n
等式约束

s.t

等式+不等式约束问题

s.t hv(x)=0,v=1,2,...,p<n

3、惩罚函数法定义
惩罚函数法（SUMT法）又称序列无约束极小化技术，将等式约束与不等式约束的条件，经过适当定义的复合函数加到原目标函数上构造了惩罚函数，从而取消了约束，转而求解一系列无约束优化问题。

按照惩罚函数再优化过程中的迭代点是否在约束条件的可行域内，又分为内点法、外点法和混合法

内点法：迭代点再约束条件的可行域之内，只用于不等式约束。

外点法：迭代点再约束条件的可行域之外，既用于不等式约束又可用于等式约束。

4、外点惩罚函数法
等式约束：

s.t h1(x)=x1−2=0,h2(x)=x2+3=0

算法步骤

a、构造惩罚函数：F=f+M * { [ h1(x) ]^2 + [ h2(x) ]^2 } ，式中M为初始惩罚因子；

b、然后用无约束优化极值算法求解(牛顿法)；

c、如果相邻两次惩罚函数无约束最优点之间的距离足够小【norm(x1-x0)<eps】，则收敛；

否则放大惩罚因子M=C*M，式中C为罚因子放大系数；

d、转步骤a继续迭代；

2.代码

主程序：

clear
f ='f1209';
x0=[3 0];
TolX = 1e-4;
TolFun = 1e-9;
MaxIter=100;
alpha0 = 1;
%%%%选用不是基于梯度的无约束最优化方法求解，的正确结果
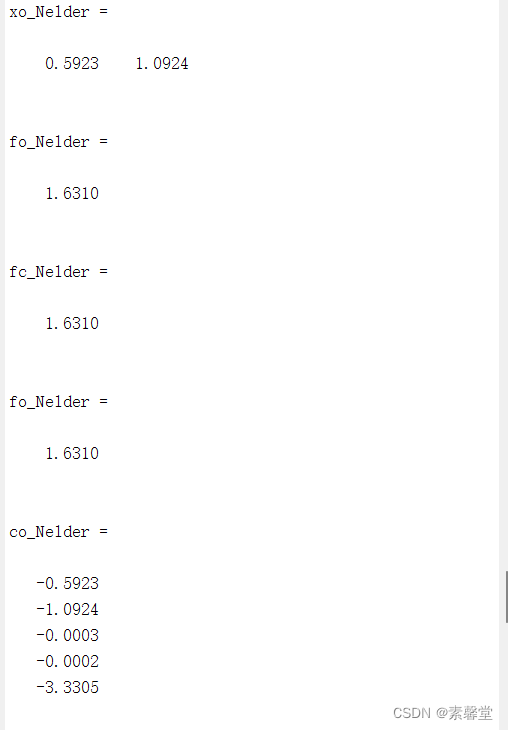
[xo_Nelder,fo_Nelder] = Opt_Nelder(f,x0,TolX,TolFun,MaxIter) %Nelder 方法
[fc_Nelder,fo_Nelder,co_Nelder] = f1209(xo_Nelder) %Nelder方法结果
[xo_s,fo_s] = fminsearch(f,x0) %MATLAB 内置函数fminsearch()
[fc_s,fo_s,co_s] = f1209(xo_s) %相应的结果
%%%基于梯度的方法最速下降法等，得到错误结果
grad=inline('[2*(x(1)+1)*((x(1)-1.2)^2+0.4*(x(2)-0.5)^2)+((x(1)+1)^2+4*(x(2)-1.5)^2)*2*(x(1)-1.2),8*(x(2)-1.5)*((x(1)-1.2)^2+0.4*(x(2)-0.5)^2)+((x(1)+1)^2+4*(x(2)-1.5)^2)*0.8*(x(2)-0.5)]','x');
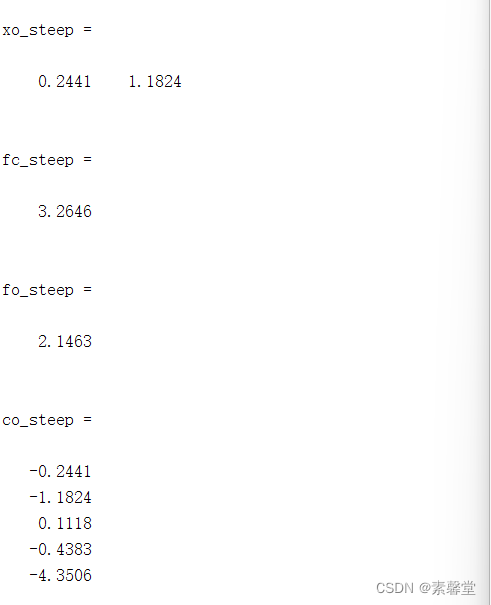
xo_steep = Opt_Steepest(f,grad,x0,TolX,TolFun,alpha0) %最速下降法
[fc_steep,fo_steep,co_steep] = f1209(xo_steep) %相应结果
[xo_u,fo_u] = fminunc(f,x0); % MATLAB 内置函数fminunc()
[fc_u,fo_u,co_u] = f1209(xo_u) %相应结果

子程序：

function [xo,fo] =Opt_Nelder(f,x0,TolX,TolFun,MaxIter)
%Nelder-Mead法用于多维变量的最优化问题，维数>=2.
N = length(x0);
if N == 1 %一维情况，用二次逼近计算
[xo,fo] = Opt_Quadratic(f,x0,TolX,TolFun,MaxIter);
return
end
S = eye(N);
for i = 1:N %自变量维数大于2时，重复计算每个子平面的情况
i1 = i + 1;
if i1 > N
i1 = 1;
end
abc = [x0; x0 + S(i,:); x0 + S(i1,:)]; %每一个定向子平面
fabc = [feval(f,abc(1,:)); feval(f,abc(2,:)); feval(f,abc(3,:))];
[x0,fo] = Nelder0(f,abc,fabc,TolX,TolFun,MaxIter);
if N < 3 %二维情况不需重复
break;
end
end
xo = x0;