文章目录
- 【LeetCode热题100】打卡第45天:倒数第24~20题
- ⛅前言
- 最佳卖股票时机含冷冻期
- 🔒题目
- 🔑题解
- 戳气球
- 🔒题目
- 🔑题解
- 零钱兑换
- 🔒题目
- 🔑题解
- 打家劫舍III
- 🔒题目
- 🔑题解
- 比特位计数
- 🔒题目
- 🔑题解
【LeetCode热题100】打卡第45天:倒数第24~20题
⛅前言
大家好,我是知识汲取者,欢迎来到我的LeetCode热题100刷题专栏!
精选 100 道力扣(LeetCode)上最热门的题目,适合初识算法与数据结构的新手和想要在短时间内高效提升的人,熟练掌握这 100 道题,你就已经具备了在代码世界通行的基本能力。在此专栏中,我们将会涵盖各种类型的算法题目,包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等,并会提供详细的解题思路以及Java代码实现。如果你也想刷题,不断提升自己,就请加入我们吧!QQ群号:827302436。我们共同监督打卡,一起学习,一起进步。
博客主页💖:知识汲取者的博客
LeetCode热题100专栏🚀:LeetCode热题100
Gitee地址📁:知识汲取者 (aghp) - Gitee.com
题目来源📢:LeetCode 热题 100 - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台
PS:作者水平有限,如有错误或描述不当的地方,恳请及时告诉作者,作者将不胜感激
最佳卖股票时机含冷冻期
🔒题目
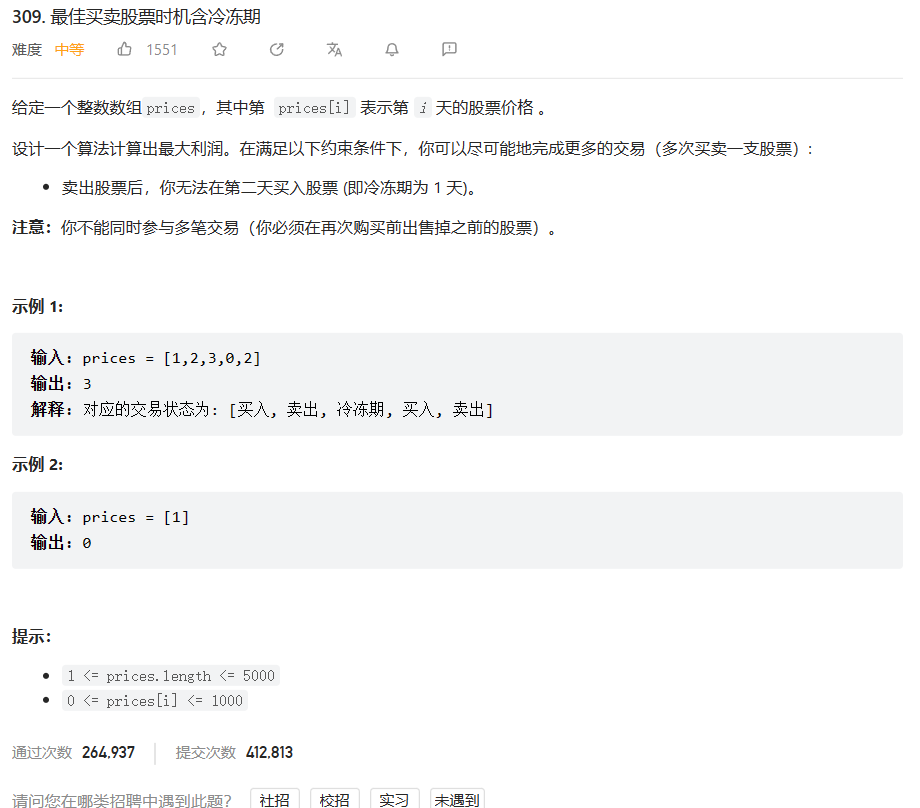
原题链接:309.最佳卖股票时机含冷冻期
🔑题解
回看前面这一题:【LeetCode热题100】打卡第31天:买卖股票的最佳时机
-
解法一:动态规划
买卖股票,由三个状态,买入、卖出、冷冻期,所以涉及到两个状态的转移
-
不持有股票。可以使用
dp[i][0]表示,代表第i+1天在不持有股票的情况下能够获得的最大收益,这也分为两种情况①情况一,昨天持有股票,但昨天卖了,今天处于冷冻期,不能买入股票,此时的状态转移方程是
dp[i][0]=dp[i-1][0],表示今天的最大收益就是昨天的最大收益,因为今天处于冻结期不能买入股票②情况二,昨天没有卖出股票,当前可以直接再卖出股票,此时的状态转移方程是
dp[i][0]=dp[i-1][1]+preices[i],表示今天的最大收益是昨天持有股票的最大收益加上今天卖出股票的收益①和②可以直接合并,也就是
Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]) -
持有股票。可以使用
dp[i][1]表示,代表第i+1天在持有股票的情况下能够获的的最大利益,同样也分为两种情况①情况一,昨天持有股票,今天没有卖出,今天持有的股票是昨天的,所以今天的最大收益就是昨天的最大收益,状态转移方程是
dp[i][1]=dp[i-1][1]②情况二,昨天没有持有股票,今天持有的股票是今天刚买入的,但是我们需要确保今天能否买入股票(也就是判断当前是否处于冷冻期),所以我们要求昨天不能卖出股票以确保今天没有处于冷冻期,那么该如何保障昨天不能卖出股票呢?这是本题的难点所在。这里给出我的分析:昨天不持有股票,由于昨天不持有股票,所以昨天可能卖出了股票,这显然不是我们所想要的,所以我们要求昨天的股票不能卖出,那么昨天不持有股票的状态是前天的(股票不是在昨天卖出的,是前天卖出的,所以今天就不会处于冷冻期了),然后今天持有的股票是今天买入的,所以就有
dp[i][1]=dp[i-2][0]-prices[i],表示当前持有股票的最大收益是前天不持有股票的最大收益减去今天买入股票的费用①和②可以合并,也就是
dp[i][1] = max(dp[i - 1][1], dp[i - 2][0] - prices[i]
初始状态:第一天不进行任何交易
dp[0][0] = 0,第一天持有一股dp[0][1] = -prices[0]所以经过不断的状态转移,我们可以得到最后一天(第n天)的最大收益是
dp[n-][0],最后一天我们不需要再买入股票了,如果要买入股票反而又要掏钱,所以最后一天的最大收益是不持有股票的状态PS:不知道为什么这类题目理解起来感觉没什么难度,为什么就是写不出w(゚Д゚)w
当
prices = [1,2,3,0,2],状态数组为: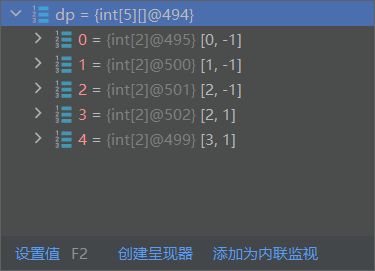
/*** @author ghp* @title* @description*/ class Solution {public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][2];// 初始状态dp[0][0] = 0;dp[0][1] = -prices[0];// 遍历每一天for (int i = 1; i < n; i++) {// 更新今天不持有股票的最大收益(昨天不持有 | 今天不持有)dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);// 更新今天持有股票的最大收益(昨天持有 | 今天持有)dp[i][1] = Math.max(dp[i - 1][1], ((i - 2) < 0 ? 0 : dp[i - 2][0]) - prices[i]);}// 第n天最大收益是不持有股票的状态return dp[n - 1][0];} }复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
代码优化:空间优化
我们可以发现当前状态,至于前一个状态有关,还有前前一个状态有关,所以完全可以使用变量来记录,从而解决内存开销
class Solution {public int maxProfit(int[] prices) {int n = prices.length;// 今天不持有股票的最大收益int curUnHold = 0;// 今天持有股票的最大收益int curHold = -prices[0];// 前天不持有股票的最大收益int prePreUnHold = 0;for (int i = 1; i < n; i++) {// 临时变量保存今天不持有股票的最大收益int temp = curUnHold;curUnHold = Math.max(curUnHold, curHold + prices[i]);curHold = Math.max(curHold, prePreUnHold - prices[i]);prePreUnHold = temp;}return curUnHold;} }复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) O(1) O(1)
其中 n n n 为数组中元素的个数
-
戳气球
🔒题目
原题链接:312.戳气球
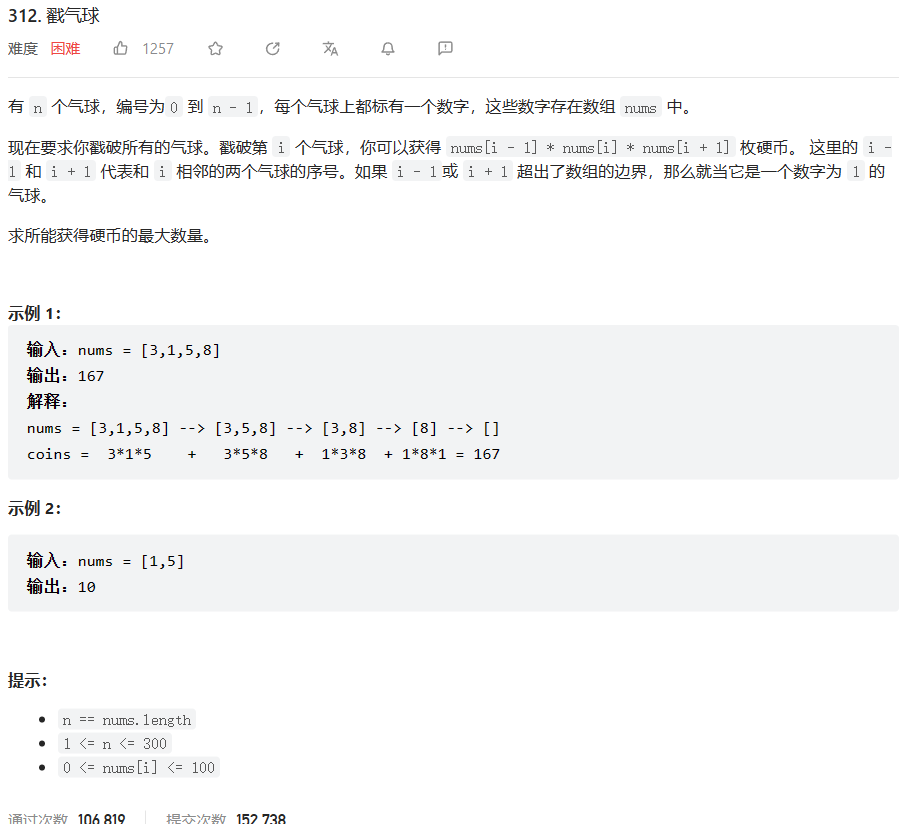
🔑题解
-
解法一:暴力DFS(超时 23 / 73 )
初看这一题就应该要知道,这一题可以使用DFS解题(别问我怎么知道的,读题O(∩_∩)O)。很容易想象出这一题的搜索空间树是怎么样的,每一层都可以枚举所有的节点,但是下一层无法使用上层使用过的节点(图我就不画了),这时候我们只需要枚举每一条路径,然后计算出每条路径的最大值,没遍历完一条路径就更新当前最大值即可,但是需要注意的是当前没遍历一个节点,当前节点就要消失,这里我们可以选择使用List集合,每次遍历就删除对应位置的元素,遍历完再添加,从而实现回溯
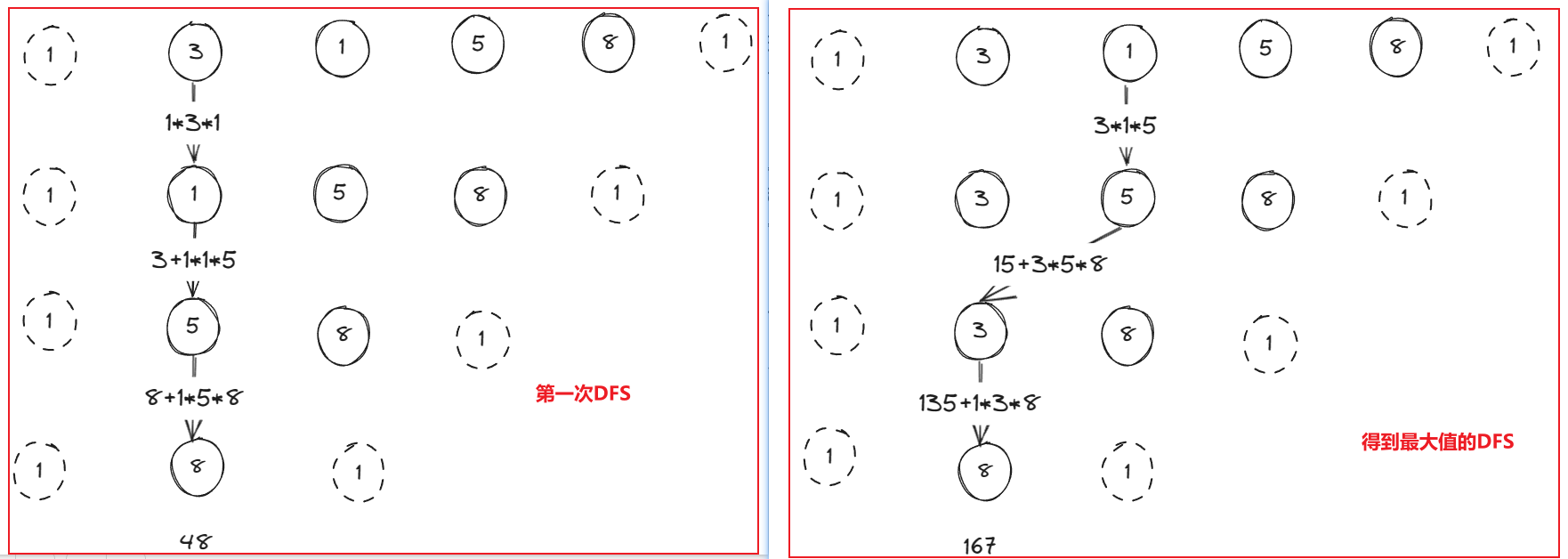
import java.util.Arrays; import java.util.List; import java.util.stream.Collectors;/*** @author ghp* @title* @description*/ class Solution {private int max = Integer.MIN_VALUE;public int maxCoins(int[] nums) {List<Integer> list = Arrays.stream(nums).boxed().collect(Collectors.toList());// 在list的前后各加一个1,防止索引越界list.add(0, 1);list.add(list.size(), 1);dfs(list, 0, nums.length, 0);return max;}private void dfs(List<Integer> list, int depth, int maxDepth, int preCoins) {if (depth == maxDepth) {// 已达最大深度,结束搜索max = Math.max(max, preCoins);return;}for (int i = 1; i < list.size() - 1; i++) {// 戳破第i个气球,并计算当前能够获得的硬币数,然后移除这个气球Integer value = list.get(i);int curCoins = list.get(i - 1) * value * list.get(i + 1);list.remove(i);dfs(list, depth + 1, maxDepth, preCoins + curCoins);// 恢复现场,用于回溯list.add(i, value);}} }复杂度分析:
- 时间复杂度: O ( n ! ) O(n!) O(n!)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
代码优化:时间优化
前面我们直接使用暴力DFS,时间复杂度高达 O ( n ! ) O(n!) O(n!),这是常见的时间复杂度从小到大的一个排行 O ( 1 ) < O ( l o g n ) < O ( n ) < O ( n l o g n ) < O ( n 2 ) < O ( n 3 ) < O ( 2 n ) < O ( n ! ) O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)< O(n!) O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!),当前处于最高阶,所以耗时是是非高的,对于DFS优化,我们有很多手段,常见的比如:剪枝、记忆搜索(也属于剪枝的一种)。这里我们选择使用记忆搜索+分治的的方式进行优化,同时将List替换成Array方便实现分治。
但是这里我们需要考虑一下记忆数组memo应该存什么,如果模拟戳气球,那么会导致区间不连续,比如[0, n-1]这个区间,选择一个i气球戳破,那么区间分裂成[0, i-1]和[i+1, n-1],那么此时对于气球i-1来说,它的左右气球变成了i-1和i+1,随着气球不断被戳破,这种关系变得很繁琐。所以我们可以逆向思维考虑一下,戳破所有气球变成从0开始放置气球,为了更好进行边界处理,我们给原本的nums数组头和尾加上1,得到一个新的数组a。
/*** @author ghp* @title* @description*/ class Solution {public int maxCoins(int[] nums) {// 初始化数组,前后各加一个1,防止索引越界int[] arr = new int[nums.length + 2];arr[0] = 1;arr[arr.length - 1] = 1;for (int i = 0; i < nums.length; i++) {arr[i + 1] = nums[i];}// DFS搜索得到最大值return dfs(arr, 0, arr.length - 1, new Integer[arr.length][arr.length]);}public int dfs(int[] arr, int left, int right, Integer[][] memo) {if (memo[left][right] != null) {// 如果当前区间已经被计算过了,就直接返回return memo[left][right];}// 当前最大能够获得的硬币数int max = 0;// DFS搜索每一个区间for (int i = left + 1; i < right; i++) {// 当前区间最大值int curMax = arr[left] * arr[i] * arr[right];// 左侧区间最大值int leftMax = dfs(arr, left, i, memo);// 右侧区间最大值int rightMax = dfs(arr, i, right, memo);// 更新当前最大可获得硬币数max = Math.max(max, leftMax + curMax + rightMax);}// 缓存[left,right]这个区间能够获得最大硬币的数量memo[left][right] = max;return max;} }复杂度分析:
- 时间复杂度: O ( n ! ) O(n!) O(n!)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
-
解法二:动态规划
class Solution {public int maxCoins(int[] nums) {int n = nums.length;int[][] rec = new int[n + 2][n + 2];int[] val = new int[n + 2];val[0] = val[n + 1] = 1;for (int i = 1; i <= n; i++) {val[i] = nums[i - 1];}for (int i = n - 1; i >= 0; i--) {for (int j = i + 2; j <= n + 1; j++) {for (int k = i + 1; k < j; k++) {int sum = val[i] * val[k] * val[j];sum += rec[i][k] + rec[k][j];rec[i][j] = Math.max(rec[i][j], sum);}}}return rec[0][n + 1];} }作者:LeetCode-Solution 链接:https://leetcode.cn/problems/burst-balloons/solution/chuo-qi-qiu-by-leetcode-solution/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。复杂度分析:
- 时间复杂度: O ( n 3 ) O(n^3) O(n3)
- 空间复杂度: O ( n 2 ) O(n^2) O(n2)
其中 n n n 为数组中元素的个数
零钱兑换
🔒题目
原题链接:322.零钱兑换
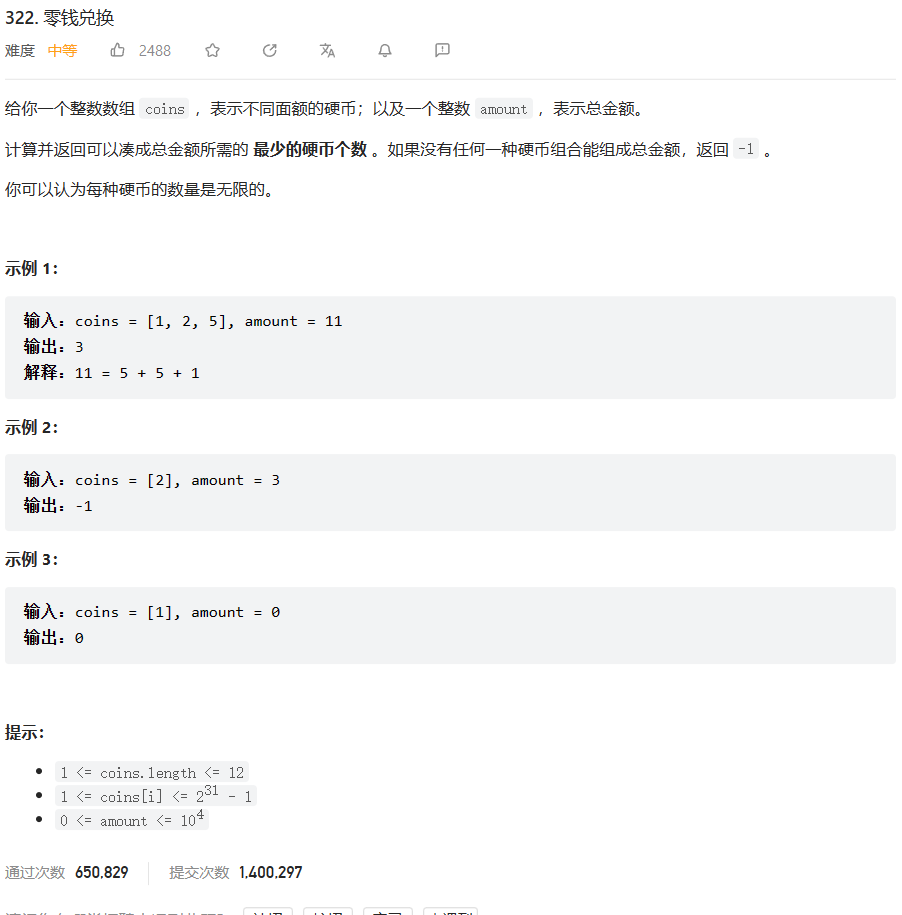
🔑题解
-
解法一:暴力DFS(超时)
/*** @author ghp* @title* @description*/ class Solution {private int minCount = Integer.MAX_VALUE;public int coinChange(int[] coins, int amount) {dfs(coins, amount, 0, 0);return minCount == Integer.MAX_VALUE ? -1 : minCount;}private void dfs(int[] coins, int amount, int sum, int count) {if (sum > amount || count >= minCount) {return;}if (sum == amount) {minCount = Math.min(minCount, count);return;}for (int i = 0; i < coins.length; i++) {dfs(coins, amount, sum + coins[i], count + 1);}} }复杂度分析:
- 时间复杂度: O ( S n ) O(Sn) O(Sn)
- 空间复杂度: O ( S ) O(S) O(S)
S是金额,n是面额数
代码优化:时间优化
这里使用记忆化搜索进行优化,我们可以缓存每次计算剩余额度可以换取的最少硬币数,这样就不用每次都去计算了
/*** @author ghp* @title* @description*/ class Solution {public int coinChange(int[] coins, int amount) {if (coins.length == 0) {return -1;}// 记忆数组 memo[i]表示剩余额度为(i+1)时能够换取成功的最少硬币数int[] memo = new int[amount];return dfs(coins, amount, memo);}public int dfs(int[] coins, int amount, int[] memo) {if (amount <= 0) {// 剩余额度小于等于0,说明已经无法换取,等于0表示换取成功 小于0表示换取失败return amount == 0 ? 0 : -1;}if (memo[amount - 1] != 0) {// 剩余换取额度已经计算过了,直接返回return memo[amount - 1];}// 当前能够换取成功所需的最少硬币数int min = Integer.MAX_VALUE;// DFS搜索每一种换取可能for (int i = 0; i < coins.length; i++) {int res = dfs(coins, amount - coins[i], memo);if (res >= 0 && res < min) {// 加1,是为了加上得到res结果的那个步骤中,兑换的一个硬币min = res + 1;}}// 缓存当前额度可以换取成功的最少硬币数memo[amount - 1] = (min == Integer.MAX_VALUE ? -1 : min);return memo[amount - 1];} }复杂度分析:
- 时间复杂度: O ( S n ) O(Sn) O(Sn)
- 空间复杂度: O ( S ) O(S) O(S)
S是金额,n是面额数
-
解法二:动态规划
一般能够使用记忆搜索的都可以使用动态规划,记忆搜索是自顶向下,动态规划是自底而上
class Solution {public int coinChange(int[] coins, int amount) {// 自底向上的动态规划if(coins.length == 0){return -1;}// memo[n]表示的凑成总金额为n所需的最少的硬币个数int[] memo = new int[amount+1];memo[0] = 0;for(int i = 1; i <= amount;i++){int min = Integer.MAX_VALUE;for(int j = 0;j < coins.length;j++){if(i - coins[j] >= 0 && memo[i-coins[j]] < min){min = memo[i-coins[j]] + 1;}}memo[i] = min;}return memo[amount] == Integer.MAX_VALUE ? -1 : memo[amount];} }复杂度分析:
- 时间复杂度: O ( S n ) O(Sn) O(Sn)
- 空间复杂度: O ( S ) O(S) O(S)
S是金额,n是面额数
打家劫舍III
🔒题目
原题链接:337.打家劫舍III
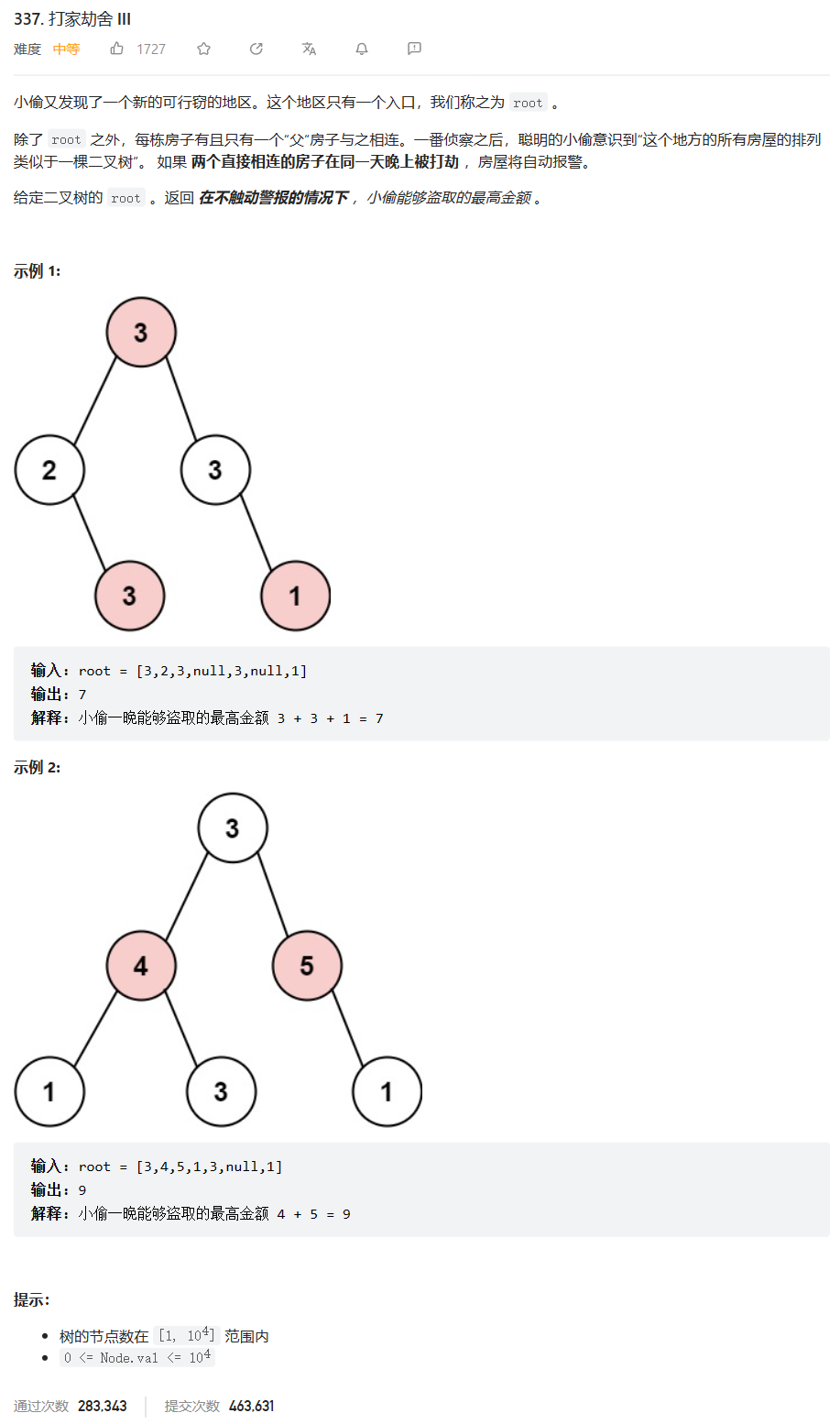
🔑题解
可以回看:【LeetCode热题100】打卡第36天:打家劫舍
-
解法一:暴力(超时)
暴力的思路很简单,实现起来也相对简单
- 从根节点出发
- 遍历左子树,遍历需要间隔一个节点
- 遍历右子树,遍历需要间隔一个节点
1、2、3递归进行,最终通过递归所有的路径,即可计算出最大值
这个遍历的过程类似于中序遍历
关于中序遍历可以参考这篇文章: 【LeetCode热题100】打卡第27天:二叉树的前序、中序、后序遍历
/*** @author ghp* @title* @description*/class Solution {public int rob(TreeNode root) {if (root == null) {return 0;}int money = root.val;if (root.left != null) {// 计算左子节点的最大值money += (rob(root.left.left) + rob(root.left.right));}if (root.right != null) {// 计算右子节点的最大值money += (rob(root.right.left) + rob(root.right.right));}// 判断是包含当前根节点的值大,还是不包含根节点的值最大return Math.max(money, rob(root.left) + rob(root.right));} }复杂度分析:
- 时间复杂度: O ( 2 n ) O(2^n) O(2n)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为树的节点个数
代码优化:时间优化
针对上面那种暴力递归速度太慢的问题,经过分析其实现,我们发现爷爷在计算自己能偷多少钱的时候,同时计算了 4 个孙子能偷多少钱,也计算了 2 个儿子能偷多少钱。这样在儿子当爷爷时,就会产生重复计算一遍孙子节点。
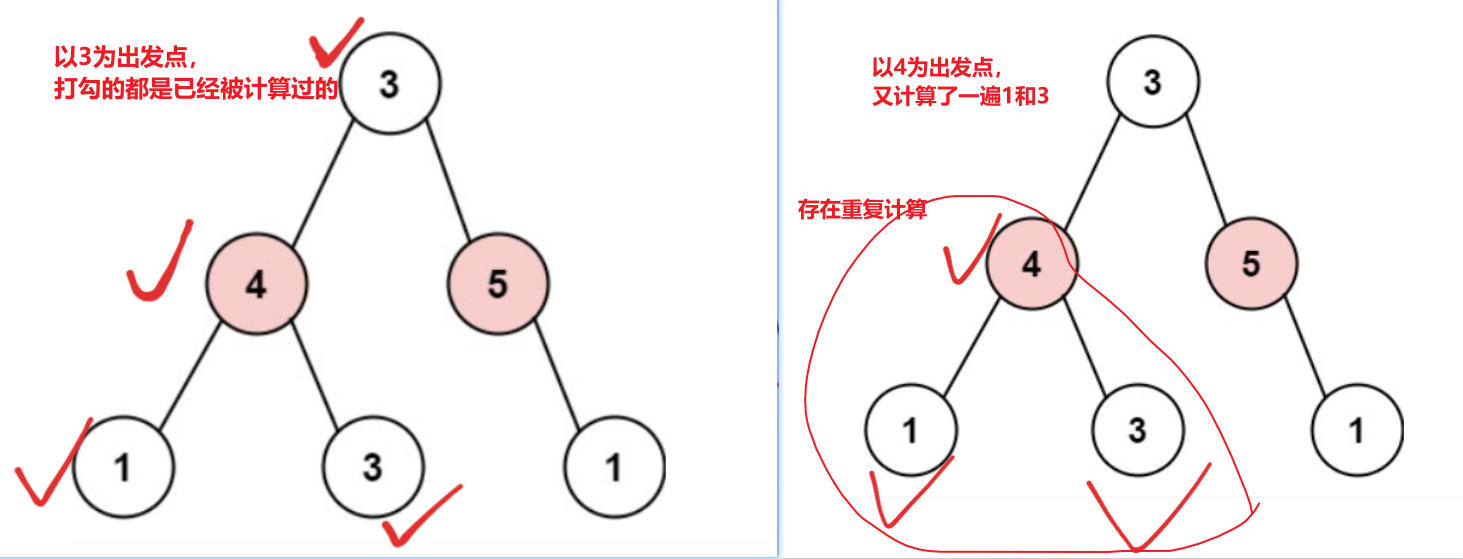
解决方案是,在遍历的同时,缓存我们计算过的节点,这里我们使用一个Map集合作为缓存容器
/*** @author ghp* @title* @description*/class Solution {public int rob(TreeNode root) {// key为当前计算的节点,value为当前节点的最大值HashMap<TreeNode, Integer> memo = new HashMap<>();return rob(root, memo);}public int rob(TreeNode root, HashMap<TreeNode, Integer> memo) {if (root == null) {return 0;}if (memo.containsKey(root)) {return memo.get(root);}int money = root.val;if (root.left != null) {money += (rob(root.left.left, memo) + rob(root.left.right, memo));}if (root.right != null) {money += (rob(root.right.left, memo) + rob(root.right.right, memo));}// 缓存当前节点的最大值int result = Math.max(money, rob(root.left, memo) + rob(root.right, memo));memo.put(root, result);return result;} }复杂度分析:
- 时间复杂度: O ( 2 n ) O(2^n) O(2n),通过剪枝,虽然不能降低时间复杂度,但是可以大幅提高搜索速度,搜索耗时也会远远低于这个时间复杂度
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为树的节点个数
-
解法二:动态规划
一般能够使用记忆搜索的都可以使用动态规划,记忆搜索是自顶向下,动态规划是自底向上。
每个节点可选择偷或者不偷两种状态,根据题目意思,相连节点不能一起偷当前节点选择偷时,那么两个孩子节点就不能选择偷了,
当前节点选择不偷时,两个孩子节点只需要拿最多的钱出来就行(两个孩子节点偷不偷没关系)我们使用一个大小为 2 的数组来表示int[] dp= new int[2],dp[0]代表不偷,dp[1]代表偷,那么就有以下两种情况:- 当前节点选择不偷,当前节点能够偷的最大值就是左边孩子能够偷的最大值加上右边孩子能够偷的最大值,此时动态转移方程是
dp[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) + Math.max(rob(root.right)[0], rob(root.right)[1]),其中rob(root.left)[0]表示左侧孩子不偷的最大值,rob(root.left)[1]表示左侧孩子偷的最大值 - 当前节点选择偷,当前节点能够偷的最大值就是左边孙子的最大值加上右边孙子的最大值,此时的动态转移方程为
dp[1] = rob(root.left)[0] + rob(root.right)[0] + root.val
对应的代码如下:
/*** @author ghp* @title* @description*/class Solution {public int rob(TreeNode root) {int[] dp = dfs(root);return Math.max(dp[0], dp[1]);}public int[] dfs(TreeNode root) {if (root == null) {return new int[2];}int[] dp = new int[2];// 左节点最大值int[] left = dfs(root.left);// 右节点最大值int[] right = dfs(root.right);// 不偷root的最大值dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);// 偷root的最大值dp[1] = left[0] + right[0] + root.val;return dp;} }复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
- 当前节点选择不偷,当前节点能够偷的最大值就是左边孩子能够偷的最大值加上右边孩子能够偷的最大值,此时动态转移方程是
比特位计数
🔒题目
原题链接:338.比特位计数

🔑题解
-
解法一:动态规划
这个动态规划,其实就是找规律
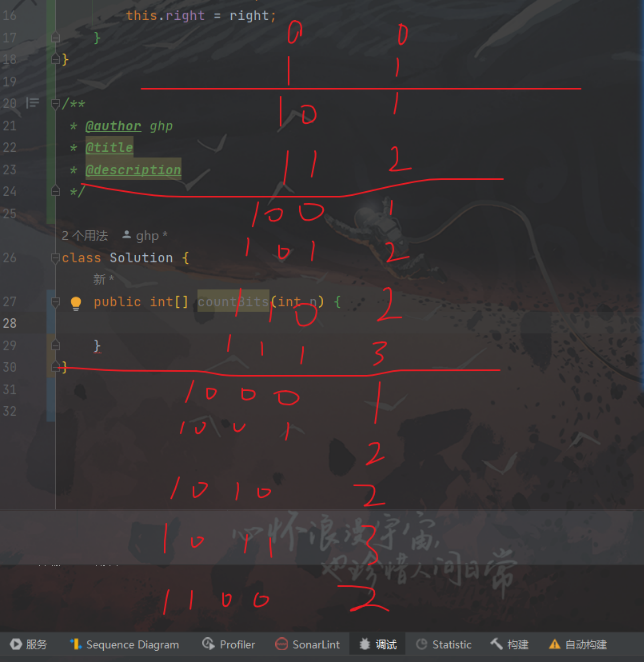
设
dp[i]为第 (i+1) 个元素的二进制表示中含有1的个数,从上图我们可以发现从第 3 个元素(也就是2开始),每次1的数量都等于,1加上第一个树1出现的数量,比如- 10(也就是2)它的1出现的数量是 第1个数 0 出现1的数量加上1,1
- 11(也就是3)它的1出现的数量是 第2个数 1 出现1 的数量加上1,2
- 100(也就是4)它的出现的数量是 第1个数 0 出现1 的数量加上1,1
- 101(也就是5)它的出现的数量是 第2个数 1 出现1 的数量加上1,2
- 110(也就是6)它的出现的数量是 第3个数 10 出现1 的数量加上1,2
- 111(也就是7)它的出现的数量是 第4个数 11 出现1 的数量加上1,3
……
通过上面的列举,我们可以得到动态转移方程
dp[i]=dp[j],其中 j 的取值从 0 到 i/*** @author ghp* @title* @description*/class Solution {public int[] countBits(int n) {if (n == 0) {return new int[]{0};}int[] dp = new int[n+1];dp[0] = 0;dp[1] = 1;// 记录已经计算过的数int count = 2;// 从n=2开始计算for (int i = 2; i <= n; i = count) {// 计算进位后的数,备注: (i+j)<=n是防止NPEfor (int j = 0; j < i && (i+j) <= n; j++) {dp[i + j] = 1 + dp[j];count++;}}return dp;} }复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2),由于外层循环是跳跃式的,所以时间复杂度会远小于 O ( n 2 ) O(n^2) O(n2),这比直接暴力要快很多
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
代码优化:时间优化
通过位运算进行优化,从第2个数开始,
i >> 1表示算术右移(最高位是什么就补什么)一位,相当于除以2,&是与运算(要注意和短路与&&进行区分),与运算的特点是,任何数与0运算都是0,任何数与1运算都是本身,所以i & 1是用来判断当前数是否是偶数的,如果是偶数那么当前结果为0,如果是奇数那么当前数是1- 1(也就是1), dp[1] = dp[0] + 1 = 1
- 10(也就是2), dp[2] = dp[1] + 0 = 1
- 11(也就是3), dp[3] = dp[1] + 1 = 2
- 100(也就是4), dp[4] = dp[2] + 0 = 1
- 101(也就是5), dp[5] = dp[2] + 1 = 2
- 110(也就是6), dp[6] = dp[3] + 0 = 2
- 111(也就是7), dp[7] = dp[3] + 1 = 3
……
总的来讲:奇数则前一个偶数+1,偶数直接等于折半数。完美符合题意,嘿嘿🤭
/*** @author ghp* @title* @description*/ class Solution {public int[] countBits(int n) {int[] dp = new int[n + 1];for (int i = 1; i <= n; i++) {dp[i] = dp[i >> 1] + (i & 1);}return dp;} }复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
其中 n n n 为数组中元素的个数
参考题解:
- 最佳买卖股票时机含冷冻期 - 最佳买卖股票时机含冷冻期 - 力扣(LeetCode)
- 买卖股票系列 | 带冷冻期的最大收益(动态规划) - 最佳买卖股票时机含冷冻期 - 力扣(LeetCode)
- 超详细回溯到分治到DP - 戳气球 - 力扣(LeetCode)
- 逆向思维,从暴力回溯到记忆化 - 戳气球 - 力扣(LeetCode)
- Java 递归、记忆化搜索、动态规划 - 零钱兑换 - 力扣(LeetCode)
- 三种方法解决树形动态规划问题-从入门级代码到高效树形动态规划代码实现 - 打家劫舍 III - 力扣(LeetCode)