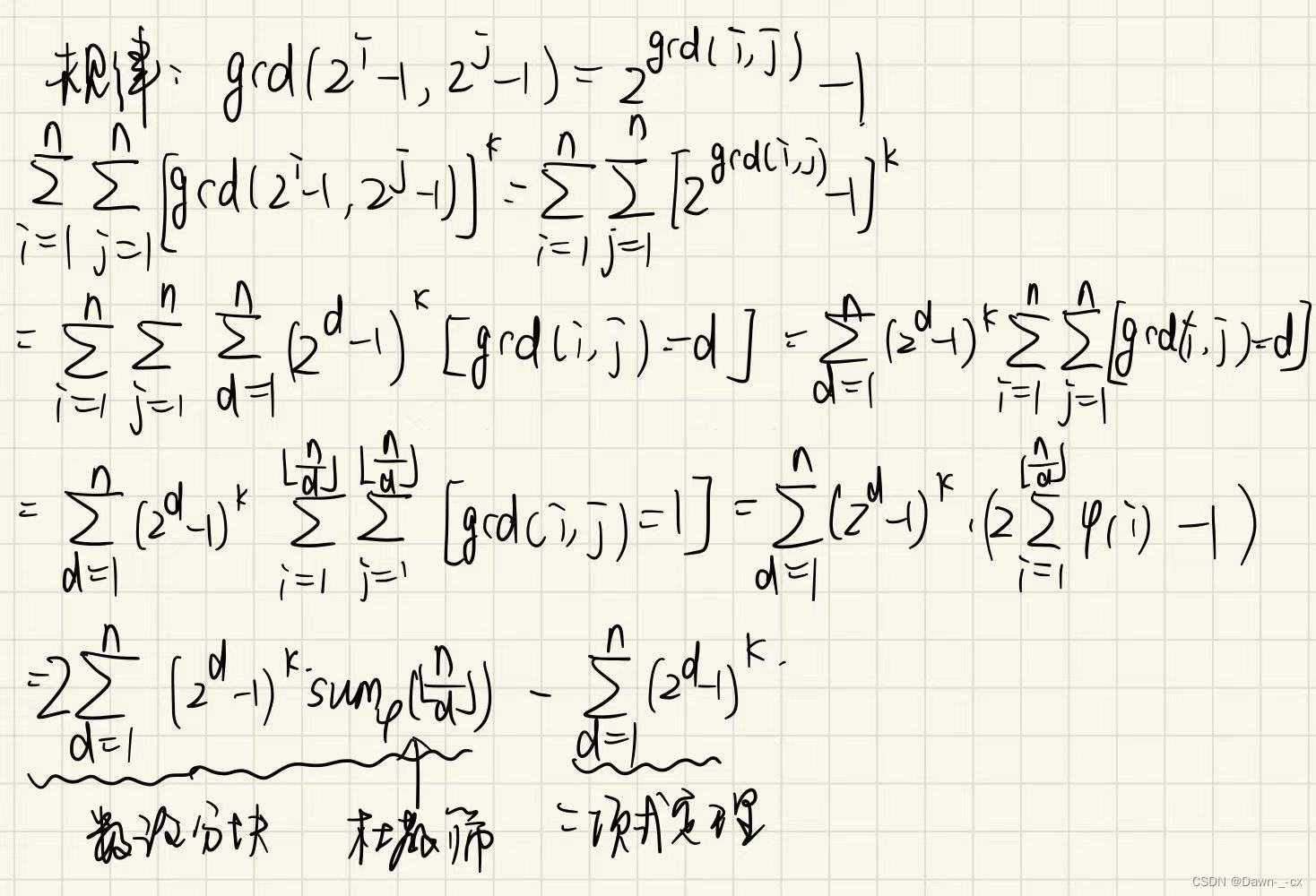给定
n个非负整数表示每个宽度为1的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

我们看到题的第一步,永远是对入参进行判断
public int trap(int[] height) {if (height == null) {return 0;}...}但是我们想想看,接雨水是不是和往桶里倒水的问题很像,倒入水的体积往往是由桶两边较低的那个高度决定的,这个问题亦是如此



由我们分析可知当数组的长度小于3的时候,是不可能接到雨水的,所以我们在判断入参条件的时候就可以这样写
public int trap(int[] height) {if (height == null || height.length < 3) {return 0;}...}刚才我们已经分析过了,一个位置的存储量只和最短的那一边有关系,边越长,我们固定位置上的存储量就越多,所以我们可以遍历每个位置,分别计算出各个位置上的存储量,再最后求和就完美的解决了本题
int count = 0;for (int i = 1; i < height.length; i++) {//找左边的最高值int lMax = 0;for (int j = 0; j < i; j++) {lMax = Math.max(lMax, height[j]);}//找到右边的最高值int rMax = 0;for (int j = i + 1; j < height.length; j++) {rMax = Math.max(rMax, height[j]);}}好了,这样我们相对位置上的两边最高的边已经求出来了,只不过现在还存一个问题,如果,当前位置的高度如果大于较小的那边高度的话,是否还可有存储水量呢?
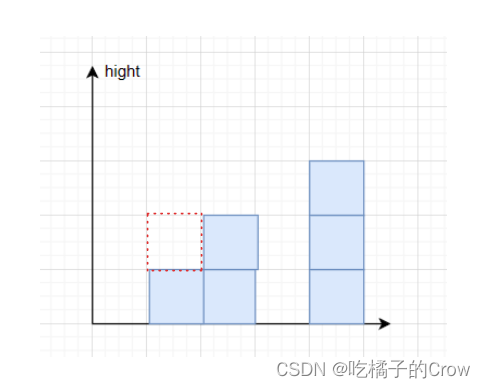
所以当前位置的高度如果大于两边最长的相对较小的边的高度,则不能进行存储水量,所以我们再对我们的代码进行完善
int count = 0;for (int i = 1; i < height.length; i++) {//找左边的最高值int lMax = 0;for (int j = 0; j < i; j++) {lMax = Math.max(lMax, height[j]);}//找到右边的最高值int rMax = 0;for (int j = i + 1; j < height.length; j++) {rMax = Math.max(rMax, height[j]);}if (Math.min(lMax, rMax) - height[i] > 0) {count += Math.min(lMax, rMax) - height[i];}}这就完成了我们所谓hard题的接雨水问题了,这个题面试中还是经常问的,希望大家透析原理,面试无压力,下面给大家奉上整个代码,供大家参考借鉴
public int trap(int[] height) {if (height == null || height.length < 3) {return 0;}int count = 0;for (int i = 1; i < height.length; i++) {//找左边的最高值int lMax = 0;for (int j = 0; j < i; j++) {lMax = Math.max(lMax, height[j]);}//找到右边的最高值int rMax = 0;for (int j = i + 1; j < height.length; j++) {rMax = Math.max(rMax, height[j]);}if (Math.min(lMax, rMax) - height[i] > 0) {count += Math.min(lMax, rMax) - height[i];}}return count;}