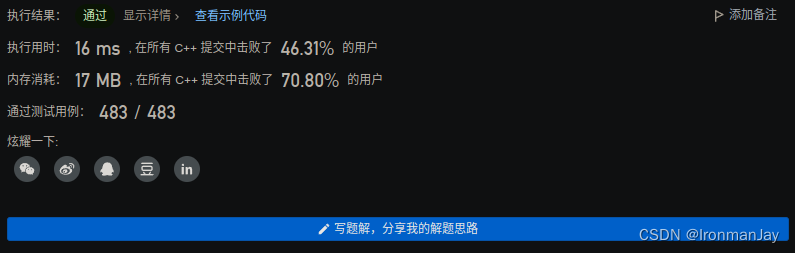
1. 线性回归
回归属于有监督学习中的一种方法。该方法的核心思想是从连续型统计数据中得到数学模型,然后
将该数学模型用于预测或者分类。该方法处理的数据可以是多维的。
回归是由达尔文的表兄弟Francis Galton发明的。Galton于1877年完成了第一次回归预测,目的是
根据上一代豌豆的种子(双亲)的尺寸来预测下一代豌豆种子(孩子)的尺寸(身高)。Galton在
大量对象上应用了回归分析,甚至包括人的身高。他得到的结论是:如果双亲的高度比平均高度
高,他们的子女也倾向于平均身高但尚不及双亲,这里就可以表述为:孩子的身高向着平均身高回
归。Galton在多项研究上都注意到了这一点,并将此研究方法称为回归。
比如:有一个房屋销售的数据如下


如果来了一个新的面积,假设在销售价钱的记录中没有的,怎么处理?
解决方法:用一条曲线去尽量准的拟合这些数据,然后如果有新的输入过来,我们可以在将曲线上
这个点对应的值返回。如果用一条直线去拟合,可能是下面的样子:

常用概念和符号:
房屋销售记录表:训练集(training set)或者训练数据(training data),是我们流程中的输入数
据,一般称为x;
房屋销售价钱:输出数据,一般称为y;
拟合的函数(或者称为假设或者模型):一般写做y=h(x)
训练数据的条目数(#training set):一条训练数据是由一对输入数据和输出数据组成的输入数据
的维度n(特征的个数,#features);
这个例子的特征是两维的,结果是一维的。然而回归方法能够解决特征多维,结果是一维多离散值
或一维连续值的问题识别结果。
注意:
(1)因为是线性回归,所以学习到的函数为线性函数,即直线函数
(2)因为是单变量,因此只有一个x;
单变量线性回归模型:

正向线性关系:

负向线性关系:

无关系:

y^=b0+b1x
这个方程叫做估计线性方程(estimated regression line)。
其中,b0是估计线性方程的纵截距,b1是估计线性方程的斜率,y^是在自变量x等于一个给定值
的时候,y的估计值。
线性回归例子:
汽车卖家做电视广告数量与卖出的汽车的数量:



假设有一周广告数量为6,则预估卖出的汽车数量为5*6+10=40。
代数推导:

矩阵推导:

2. 多元线性回归
简单线性回归与多元线性回归的区别:
1.与简单线性回归区别(simple linear regression):多个自变量x
2.多元回归模型
y=β0+β1x1+β2x2+…+βpxp+e
其中:β1, β2 … βp是参数值,e是误差值
3.多元回归方程
E(y)=β0+β1x1+β2x2+…+βpxp
4.估计多元回归方程
y_hat=b0+b1x1+b2x2+…+bpxp
一个样本用来计算β0,β1,β2.....βp的点估计b0,b1,b2.....bp
比如:一家快递公司送货
x1:运输里程 x2:运输次数 y:总运输时间


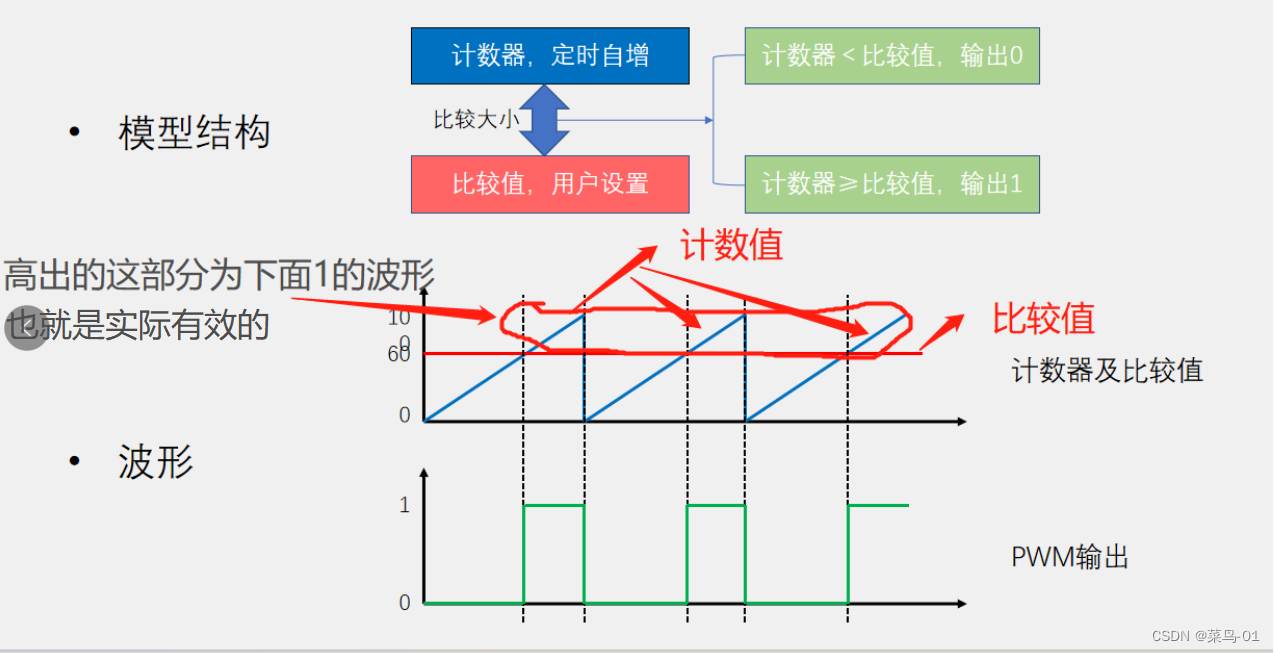
3. 代价函数
代价函数(有的地方也叫损失函数,Loss Function)在机器学习中的每一种算法中都很重要,因为
训练模型的过程就是优化代价函数的过程,代价函数对每个参数的偏导数就是梯度下降中提到的梯
度,防止过拟合时添加的正则化项也是加在代价函数后面的。一个好的代价函数需要满足两个最基
本的要求:能够评价模型的准确性,对参数可微。
在线性回归中,最常用的代价函数是均方误差(mean squared error),具体形式为:

求参数的方法:
最小二乘法:是一个直接的数学求解公式,但是他要求X是满秩的。

梯度下降法(gradient descent):
梯度下降原理:将函数比作一座山,我们站在某个山坡上,往四周看,从哪个方向向下走一小步,
能够下降的最快;
方法:
(1)先确定向下一步的步伐大小,我们称为Learning rate;
(2)任意给定一个初始值;
(3)确定一个向下的方向,并向下走预先规定的步伐,并更新初始值;
(4)当下降的高度小于某个定义的值,则停止下降;

梯度下降法的特点:
(1)初始点不同,获得的最小值也不同,因此梯度下降求得的只是局部最小值;
(2)越接近最小值时,下降速度越慢;
如果参数初始值就在local minimuml的位置,所以derivative肯定是0,因此参数值不会变化;
如果取到一个正确的α值,则cost function应该越来越小;
随时观察Q值,如果cost function变小了,则ok,反之,则再取一个更小的值。
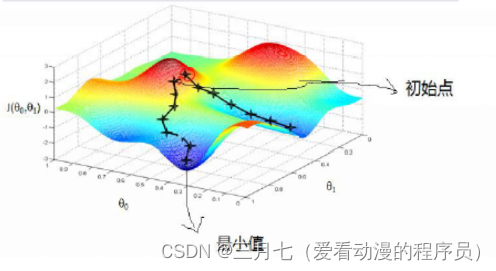
从上图可以看出,初始值不同,获得的最小值也不同,因此梯度下降求得的只是局部最小值。
下降的步伐大小非常重要,如果过小,就会找到函数最小值的速度非常的慢,如果太大,则可能出
现over shoot the minium 的现象。
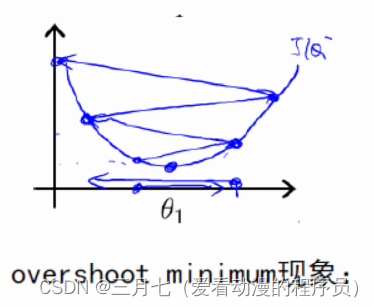
如果learning rate取值之后发现,cost function 增长了,则需要降低learning rate。

def gradientDescent(x,y,theta,alpha,m,numIterations):xTrans =x.transpose()for i in range(0,numIterations):hypothesis=np.dot(x,theta)loss=hypothesis-y#cost np.sum(loss *2)/(2 m)#print("Iteration %d Cost:%f"%(i,cost))gradient=np.dot(xTrans,loss)/mtheta=theta-alpha*gradientreturn theta