时间复杂度、空间复杂度实践练习（力扣OJ）

文章目录

前言

题目一：轮转数组

思路一：

思路二：

思路三：

题目二：消失的数字

思路一：

思路二：

思路三：

题目三：移除元素

思路：

总结

前言

想要编写高效的算法，了解时间复杂度是至关重要的。在本文中，我们将介绍一些时间复杂度和空间复杂度的练习，通过实际例子帮助您分析程序的时间复杂度和空间复杂度，前边已经了解过，复杂度是评价一个程序好坏标准，今天我们切身体验一下数据结构入门刷题。如何写出好的程序。

题目一：轮转数组

题目如下：

题目给出的示例如下：

思路一：

没做过类似题目的人，大多数人思路或许是这样的：将数组最好一个元素保存，其他元素向后移动，再将保存的元素放在最前边。这也只是这道题的其中一种解题思路。但这个思路在力扣上过不去的。

我们来分析一下这个思路：我们知道数组元素个数假设为n，但要将其他元素向后移动就需要进行n-1次，此外如果遇到最坏的情况我们需要轮转n-1次（执行n次就是原数组，n+1次就等价于轮转一次），每次执行n-1次，它的时间复杂度就是O（N^2)，空间复杂度为O（1）。由此可见这个思路的效率很低，所以这个思路我就不再实现。

思路二：

我们观察一下初始数组和输出数组的特点，就可以很容易的想到这个思路：轮转几次就把后几个数字移到前边，把前边的部分移到后边。这个方法简单粗暴。

代码实现：

void rotate(int* nums, int numsSize, int k)
{int *tmp = (int*)malloc( sizeof(int) * numsSize );k %= numsSize;memcpy(tmp,nums+numsSize-k,sizeof(int)*k);memcpy(tmp+k,nums,sizeof(int)*(numsSize-k));memcpy(nums,tmp,sizeof(int)*numsSize);free(tmp);
}

它的时间复杂度为O(N)，空间复杂度也为O(N)。用空间来换取效率，这个思路也并不是最优解。

思路三：

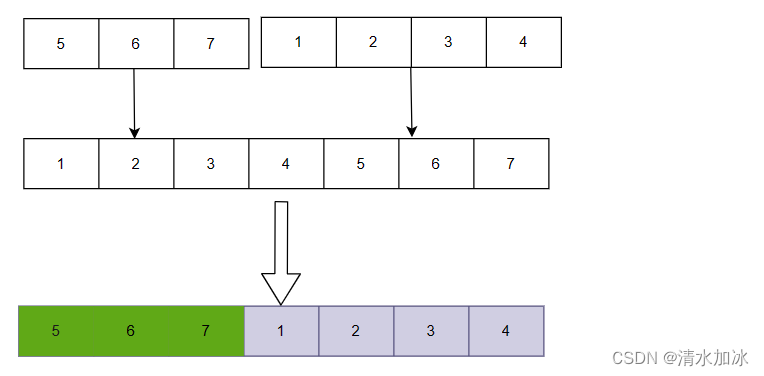
我们也可以通过将数组元素逆置的方法来达到轮转的效果思路如下：

代码实现：

void reverse(int* nums, int star, int end) {while (star < end) {int temp = nums[star];nums[star] = nums[end];nums[end] = temp;star++;end--;}
}void rotate(int* nums, int numsSize, int k) {k %= numsSize;reverse(nums, 0, numsSize - 1);reverse(nums, 0, k - 1);reverse(nums, k, numsSize - 1);
}

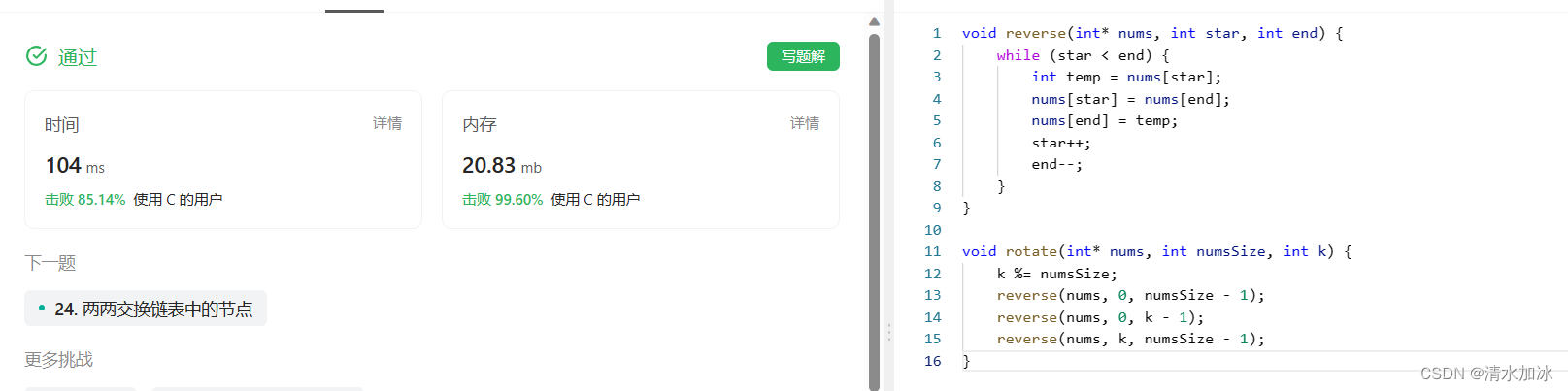
这个思路的时间复杂度为O(N),空间复杂度为O(1)。这个思路才是这道题的最优解。

题目二：消失的数字

题目描述：

思路一：

题目中说到数组包含从0到n的所有整数，但缺少其中一个。那我们就可以先对数组的元素进行排序，然后遍历，如果下一个数据不等于下一个数加一，那么下一个数就是消失的数字。思路理清之后，我们可以先看一下这个思路的复杂度如何。

复杂度也取决于排序的方法，最优的排序是使用qsort排序，时间复杂度为O（logN*N）。然后是遍历，根据大O的渐进表示法，估算出它的时间复杂度为O（logN*N）。可见这个方法的效率并不高，我们对于复杂度高的方法就不再实现。

思路二：

数组中的数据包含0到n所有整数，但缺失某一个，那我们就可以使用这个思路，将0到n看作一个等差数列，使用等差数列求和公式求和，最后将这个值依次减去数组中元素，最后的结果就是消失的数字。根据这个思路我们可以分析出它的时间复杂度是O(N)。

代码实现：

int missingNumber(int* nums, int numsSize){int n=numsSize;int ret=n*(n+1)/2;for(int i=0;i<n;i++){ret-=nums[i];}return ret;
}

思路三：

使用异或的方法，两个相同的数字异或的结果是0，并且异或符合乘法结合律，例如：1^2^1等于2，1^1^2也等于2。根据异或的这个特性，我们可以先异或0到n的所有数字，在将数组中所有元素依次异或，最终的结果就是消失的数字，根据思路我们可以估算出这个方法的时间复杂度也是O（N）。

代码实现：

int missingNumber(int* nums, int numsSize){
int ret=0;
for(int i=0;i<numsSize;i++)
{ret^=i;       ret^=nums[i];
}
return ret^numsSize;
}

异或0到n的数字与数组同时异或就会少异或最后一个数字，所有最后返回时进行异或。

题目三：移除元素

题目描述：

示例与说明：

题目要求空间复杂度是O(1)，并且数组还是无序的，返回的数组还要求是原来的顺序。看对于没做过类似题目的朋友，到这道题或许会感到头大，能想到的方法也大多数都很复杂。

不要在意力扣的题目难度标签，力扣题目显示为简单的题目不一定简单，但难度标为中等或难的题目题解思路一定复杂。

思路：

这里我向大家介绍一种很简单的方法，这种思路在其他很多场景中也是很常用的。我们可以遍历这个数组，如果数组中的元素与要删除的val值不相等就插入到数组中，如果相等就往后走。

假设要删除2。

0不等于2就插入数组，继续下一个，1与2不相等插入数组，继续向后遇到2不插入，原数组继续向后走。这个思路它的时间复杂度是O(N)。至于空间复杂度，题目要求空间复杂度为O(1)，但这个方法显然空间复杂度是O(N)，但是我们好好想一想，我们如果不选择创建新的数组，直接在原数组例插入，这样是否也可以。答案是可行的。依据这个思路我们将代码实现。

代码如下：

int removeElement(int* nums, int numsSize, int val) {int sz = numsSize;int pos=0;for (int i = 0; i < numsSize; i++){if (val != nums[i])nums[pos++]=nums[i];elsesz--;}return sz;
}