目录
1、线性表
1.1、数组
1.2、链表
1.3、栈
1.4、队列
2、散列表
3、树
3.1、二叉树
3.1.1、存储原理
3.1.2、红黑树
a、平衡二叉树和红黑树
b、红黑树特征
c、左旋
d、右旋
e、颜色反转
3.1.3、二叉堆
3.1.4、二叉树的遍历
a、深度优先遍历
b、广度优先遍历
3.2、多路查找树
3.2.1、B树
3.2.2、B+树
4、图
4.1、基本概念
4.2、图的存储
4.2.1、邻接矩阵
无向图
有向图
带权图
4.2.2、邻接表
4.3、图的遍历
4.3.1、深度优先搜索(DFS)
4.3.2、广度优先搜索(BFS)
1、线性表
1.1、数组
- 概念:有限个相同类型的变量所组成的有序集合。下标从零开始。
- 存储原理:用一组连续的内存空间来存储一组具有相同类型的数据。
- 元素访问:O(1),根据下标访问数据。首地址(假设为1000),数组类型(假设为int:4字节),那么第3个元素的地址为 1000 + (3-1)*4 = 1008。
- 操作:读取元素、更新元素、插入元素、删除元素。
- 时间复杂度:读取和更新->O(1),插入和删除->O(n)。
- 优缺点:根据下标的随机访问很高效;但插入和删除操作,可能会导致大量元素被迫移动,效率较低。扩容时,需要重新申请内存进行存储,原空间就没用了。
1.2、链表
- 概念:非连续的、非顺序的数据结构,由若干个节点组成。链表由一系列结点组成,每个结点包含一个存储元素的数据域和一个存储下一个结点地址的指针域。常见链表有单链表、双向链表、循环链表。
- 存储原理:结点在内存中随机存储,通过每个结点中的指针域,将零碎的链表空间,进行关联。
- 操作:查找结点、更新结点、插入结点、删除结点。
- 时间复杂度:查找结点->O(n),插入/更新/删除结点->O(1)。
- 优缺点:插入、删除、更新效率高,不需要连续的内存空间。但查询效率较低。
1.3、栈
- 概念:线性数据结构,栈中元素只能先入后出。最早进入的元素的位置叫做栈底,最后进入的元素的位置叫做栈顶。
- 存储原理:数组和链表都可以作为栈的底层数据结构。数组实现的栈也称为顺序栈或静态栈,链表实现的栈也称为链式栈或动态栈。
- 操作:入栈(push)、出栈(pop)。
- 时间复杂度:入栈/出栈->O(1)。
1.4、队列
- 概念:线性数据结构,队列中元素只能先入先出。队列的出口端叫做队头,队列的入口端叫做队尾。
- 存储原理:数组和链表都可以实现队列。用数组实现的队列也叫做顺序队列,用链表实现的队列也叫做链式队列。
- 操作:入队(enquene)、出队(dequeue)。
- 时间复杂度:入队/出队->O(1)。
2、散列表
- 概念:也叫做哈希表,提供了key-value的映射关系。可以通过key,高效查询出其对应的value。
- 存储原理:散列表本质上是一个数组。通过hash函数把key转换成数组下标,作用是把任意长度的输入通过散列算法转换成固定类型、固定长度的散列值。数组固定时,可快速检索;数组变化时,需要对全部数据重新hash。(可通过一致性Hash算法进行改进)
- 优缺点:读写快,但Hash表中的元素是无序的,当遇到扩容时,需要重新计算所有元素的Hash值。
- 应用:HashMap、Redis字典、布隆过滤器、位图。
-
时间复杂度
写操作:O(1) + O(m) = O(m) m为单链元素个数
读操作:O(1) + O(m) m为单链元素个数
Hash冲突写单链表:O(m)
Hash扩容:O(n) n是数组元素个数 rehash
Hash冲突读单链表:O(m) m为单链元素个数
- 操作
- 写操作(put)
向散列表插入新的键值对。
①:通过hash函数,将key转换成数组下标;
②:将键值对插入对应的数组下标所在位置。
- Hash冲突(碰撞)
不同的key通过hash函数,得到相同的数组下标,该场景就被称为Hash冲突。Hash冲突可通过如下两种方式解决:
①:开放寻址法:当一个key通过Hash函数获得的对应的数组下标已经被占用时,就寻找下一个空档位置进行存储;
②:链表法:当发生Hash冲突时,将Hash冲突的多个键值对,使用链表进行存储。
- 读操作(get)
通过给定的key,在散列表中查询对应的value。
①:通过Hash函数,将key转换成数组下标;
②:找到数组下标对应的Entry,如果key不正确,说明有Hash冲突,通过链表头遍历该单链表,根据key值找到对应value。
- Hash扩容
Capacity:HashMap的当前长度。
LoadFactor:HashMap的负载因子(阈值),默认值为0.75f。
①:数组扩容,创建一个新的Entry空数组,长度是原数组的2倍。
②:对原数组的所有元素进行再Hash,把所有元素放入新的数组中。
3、树

- 树是N(N>=0)个节点的有限集合,树的顶部有且仅有一个节点,称为根。
- 当N = 0时,称为空树。
- 当N != 0时,其余节点又可分为m个互不相交的有限集合(子树)。
- 常见的树有二叉树、多路树、堆等。
3.1、二叉树



- 二叉树:树的每个节点最多有两个孩子节点,分别称为左孩子和右孩子,且左孩子必然小于右孩子。
- 满二叉树:树的所有非叶子节点都有左右孩子,且所有叶子节点在同一层级。
- 完全二叉树:类比满二叉树,编号位置与满二叉树一样,且编号连续的树,称为完全二叉树。
- 二叉查找树:左孩子小于父节点,右孩子大于父节点。查询和插入的时间复杂度为O(logn)。
3.1.1、存储原理


- 逻辑存储结构,可使用数组和链表进行存储。
- 链表存储(常见二叉树):每个Node包含:节点数据、指向左孩子的指针、指向右孩子的指针。
- 数组存储(完全二叉树):根节点为下标为0的数组位置,然后从上往下,从左往右依次标记下标位置。若父节点下标 = n,左孩子节点下标 = 2 * n + 1,右孩子节点下标 = 2 * (n+1)。
3.1.2、红黑树
a、平衡二叉树和红黑树
- 平衡二叉树:在二叉树的基础上,每次新增节点的时候,都会通过左旋和右旋操作,来保证左子树和右子树的高度差不超过1,防止二叉树退化成链表。
- 红黑树:一种特殊的平衡二叉树。


b、红黑树特征
- 每一个节点,要么是黑色的,要么是红色的;
- 根节点是黑色的;
- 叶子节点(空)是黑色的;
- 红色节点不能连续存在;
- 从一个节点到它的任意根节点,所经过的黑色节点数必须是相同的。
在插入节点时,会通过变色和旋转两种操作,来保证红黑树满足上述五个条件。
红黑树是一种弱平衡二叉树,相对于平衡二叉树,插入和删除时旋转次数少,所以在插入和删除较多的情况下,使用红黑树;而在修改少,查找次数多的情况下,使用平衡二叉树。
c、左旋
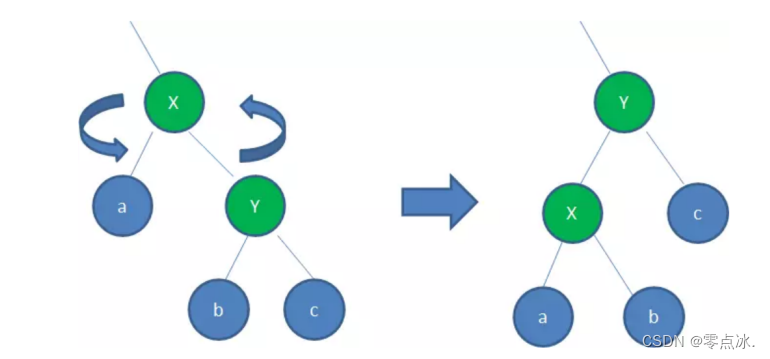
- 以X为基点逆时针旋转
- X的父节点被x原来的右孩子Y取代
- c保持不变
- Y节点原来的左孩子c变成X的右孩子
d、右旋

- 以X为基点顺时针旋转
- X的父节点被x原来的左孩子Y取代
- b保持不变
- Y节点原来的右孩子c变成X的左孩子
e、颜色反转
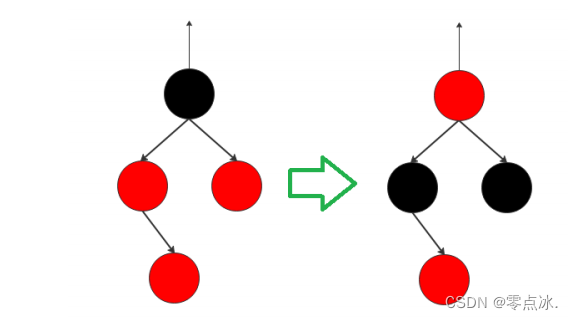
3.1.3、二叉堆

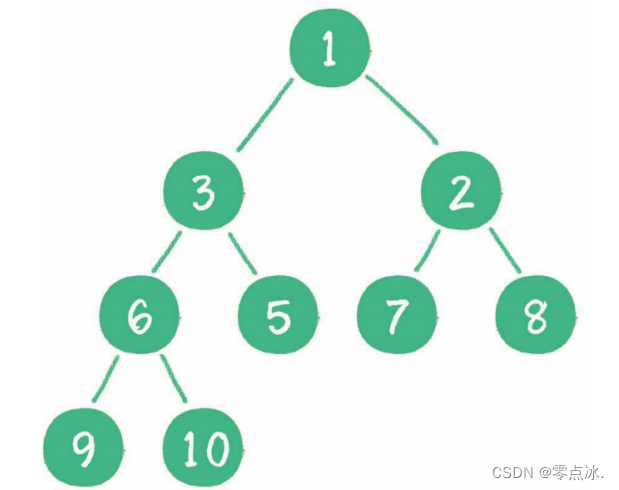

- 二叉堆本质上是一种完全二叉树。
- 大顶堆:任何一个父节点的值,都大于或等于其左、右孩子节点的值。堆顶是整个堆中的最大元素。
- 小顶堆:任何一个父节点的值,都小于或等于其左、右孩子节点的值。堆顶是整个堆中的最小元素。
- 存储原理:数组存储。完全二叉树的编号从上往下、从左往右连续,所以可直接通过数组存储。
3.1.4、二叉树的遍历

a、深度优先遍历
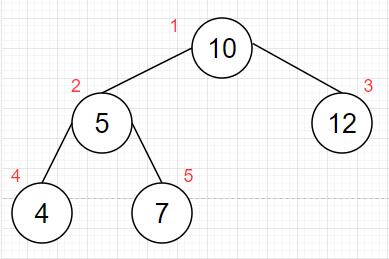
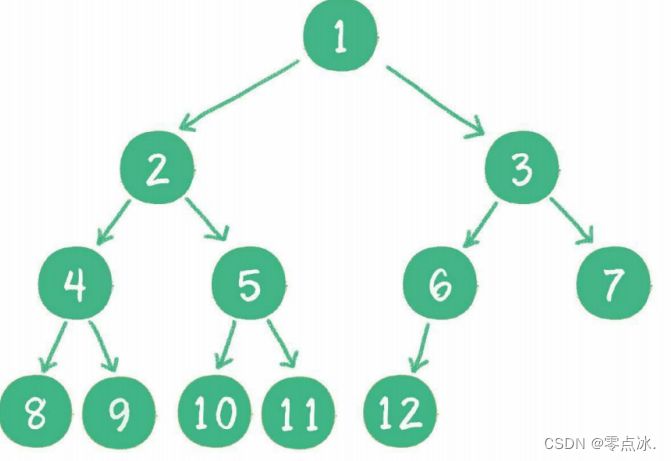
- 前序遍历(链表实现):输出顺序为:根节点->左孩子->右孩子:1 2 4 5 3 6
- 中序遍历(链表实现):输出顺序为:左孩子->根节点->右孩子:4 2 5 1 3 6
- 后序遍历(链表实现):输出顺序为:左孩子->右孩子->根节点:4 5 2 6 3 1
b、广度优先遍历
- 层序遍历(队列实现):从根节点开始,从上往下、从左往右依次遍历:1 2 3 4 5 6
3.2、多路查找树
树的每一个节点的孩子数可以多余两个,且每一个节点可以存储多个元素。
3.2.1、B树

对二叉查找树进行了改进,将相关的数据尽量集中在一起,以便一次读取多个数据,减少硬盘的操作次数。
- B树中所有节点的孩子节点数中的最大值称为B树的阶,记为M
- 树中的每个节点至多有M棵子树 ---即:如果定了M,则这个B树中任何节点的子节点数量都不能超过M
- 若根节点不是终端节点,则至少有两棵子树
- 除根节点和叶节点外,所有点至少有m/2棵子树
- 所有的叶子结点都位于同一层
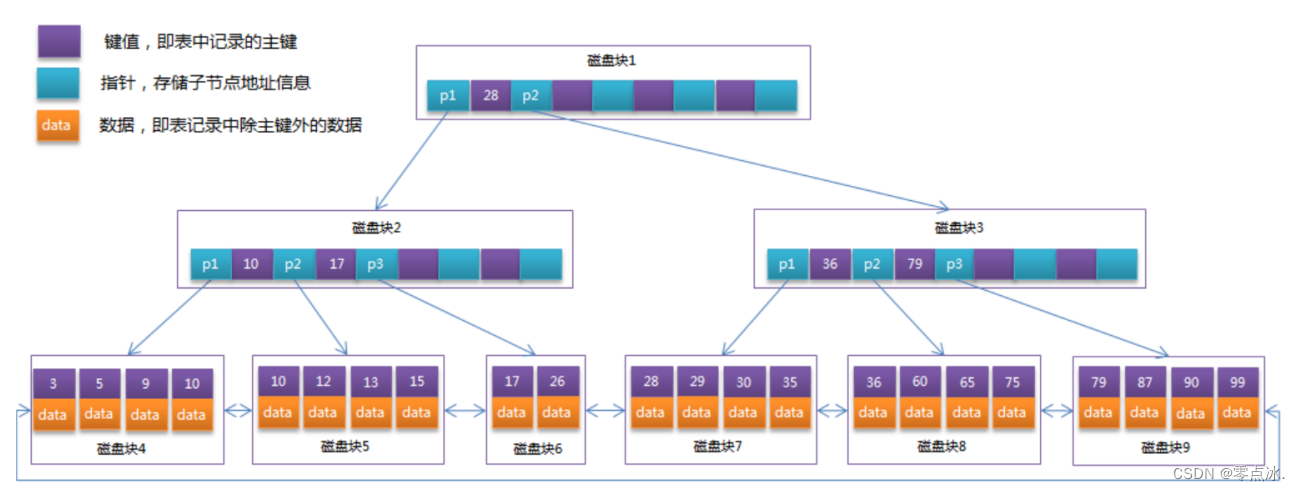
3.2.2、B+树
- 非叶子结点的子树指针与关键字个数相同
- 非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
- 为所有叶子结点增加一个链指针
- 所有关键字都在叶子结点出现
4、图
4.1、基本概念

- 一种复杂的非线性表结构。
- 顶点:图中元素叫做顶点。
- 边:两个顶点之间建立的连接关系,叫做边。
- 度:与顶点相连的边的条数叫做度。
- 有向图:边有方向的图,比如A到B的直线距离,微信的添加好友。
- 无向图:边无方向的图,比如网络拓扑图。
- 带权图:每条边都带有一个权重,可利用权重表示一些可以度量的值,比如qq两个用户之间的亲密度。
4.2、图的存储
4.2.1、邻接矩阵
邻接矩阵,底层是一个二维数组。
无向图
假设二维数组为arr[],如果顶点i与顶点j之间有边,则将arr[i][j]与arr[j][i]标记为1。
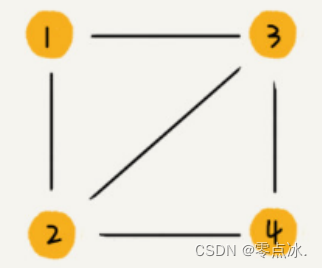

有向图
假设二维数组为arr[],如果右箭头从顶点i指向顶点j,则将arr[i][j]标记为1。


带权图
与无向图类似,只不过存储的值不是1,而是两个顶点相连的权重值。


4.2.2、邻接表
- 邻接矩阵,在存储无向图时,a[i][j] = a[j][i],浪费一半存储空间。
- 邻接表,底层结构为数组 + 链表。
- 所有顶点构成一个数组。
- 每个顶点对应一个链表,链表元素为与当前顶点相连的其他顶点值与权重。


4.3、图的遍历
4.3.1、深度优先搜索(DFS)
从起点出发,选择一个与之相连的顶点,不断向前走,直到无法继续为止;然后尝试其他未走过的顶点,直到走到终点为止。
DFS解决的是连通性的问题,即给定一个起点和一个终点,判断是否存在一条路径能从起点连接到终点。
深度优先搜索,可利用 栈(先进后出) 进行实现。

假设以顶点A为起点进行深度遍历:
- 输出A,A入栈,栈中元素为A,输出元素为A;
- 与A相连的有BDG,选择顶点B,输出B,B入栈,栈中元素为A->B,输出元素为A B;
- 与B相连的有EF,选择顶点E,输出E,E入栈,栈中元素为A->B->E,输出元素为A B E;
- 与E相连的未读取的顶点有G,输出G,G入栈,栈中元素为A->B->E->G,输出元素为A B E G;
- 没有与G相连的未读取的顶点,G出栈,栈中元素为A->B->E,输出元素为A B E G;
- 没有与E相连的未读取的顶点,E出栈,栈中元素为A->B,输出元素为A B E G;
- 与B相连的未读取的顶点有F,输出F,F入栈,栈中元素为A->B->F,输出元素为A B E G F;
- 与F相连的未读取的顶点有CD,输出C,C入栈,栈中元素为A->B->F->C,输出元素为A B E G F C;
- 与C相连的未读取的顶点有H,输出H,H入栈,栈中元素为A->B->F->C->H,输出元素为A B E G F C H;
- 没有与H相连的未读取的顶点,H出栈,栈中元素为A->B->F->C,输出元素为A B E G F C H;
- 没有与C相连的未读取的顶点,C出栈,栈中元素为A->B->F,输出元素为A B E G F C H;
- 与F相连的未读取的顶点有D,输出D,D入栈,栈中元素为A->B->F->D,输出元素为A B E G F C H D;
- 所有元素均已访问完,D出栈、F出栈、B出栈、A出栈,输出元素为A B E G F C H D。
4.3.2、广度优先搜索(BFS)
先查找离顶点最近的,然后是次近的,依次往外搜索。
BFS解决的是最短路径问题。
可使用 队列(先进先出)实现广度优先搜索。
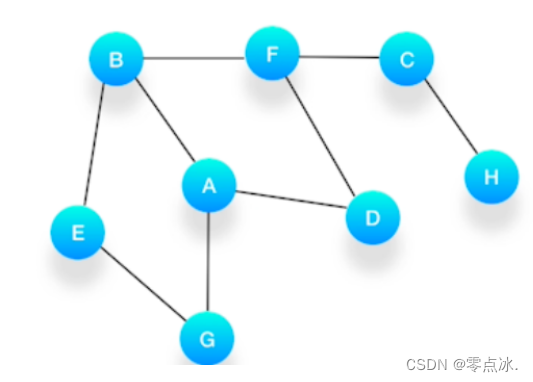
假设以顶点A为起点进行广度遍历:
- A入队,队列元素有A,输出为空;
- 输出A,A出队,放入与A相关联的BDG元素,输出为A,队列元素有BDG;
- 输出B,B出队,放入与B相关联的EF元素,输出为AB,队列元素有DGEF;
- 输出D,D出队,没有与D相关联的未读取的元素,输出为ABD,队列元素有GEF;
- 输出G,G出队,没有与G相关联的未读取的元素,输出为ABDG,队列元素有EF;
- 输出E,E出队,没有与E相关联的未读取的元素,输出为ABDGE,队列元素有F;
- 输出F,F出队,放入与F相关联的未读取的元素C,输出为ABDGEF,队列元素有C;
- 输出C,C出队,放入与C相关联的未读取的元素H,输出为ABDGEFC,队列元素有H;
- 输出H,H出队,没有与H相关联的未读取的元素,输出为ABDGEFCH,队列元素为空。
以上内容为个人学习理解,如有问题,欢迎在评论区指出。
部分内容截取自网络,如有侵权,联系作者删除。