文章目录
- 逻辑回归:
- 1 Logistic回归(二分类问题)
- 1.1 sigmoid函数
- 1.2 Logistic回归及似然函数(求解)
- 1.3 θ参数求解
- 1.4 Logistic回归损失函数
- 1.5 LogisticRegression总结
- 2 Softmax回归(多分类问题)
- 2.1 Softmax算法原理
- 2.2 Softmax算法损失函数
- 2.3 Softmax算法梯度下降法求解
- 3 总结
逻辑回归:
- 线性回归的式子作为输入
- 判断某一类别的概率(根据数据大小作出判断)
- 应用场景:二分类问题(哪一个类别少,判定的概率值是指的这个类别。)
- 返回的是概率值
1 Logistic回归(二分类问题)
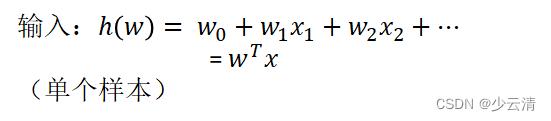
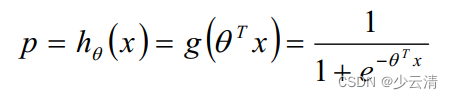
输出:[0,1]区间的概率值,默认0.5作为阀值
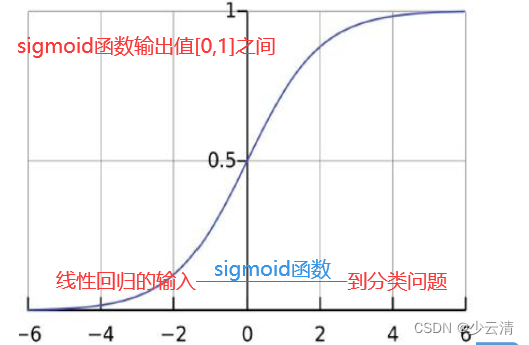
1.1 sigmoid函数
注:g(z)为sigmoid函数
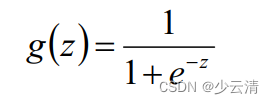
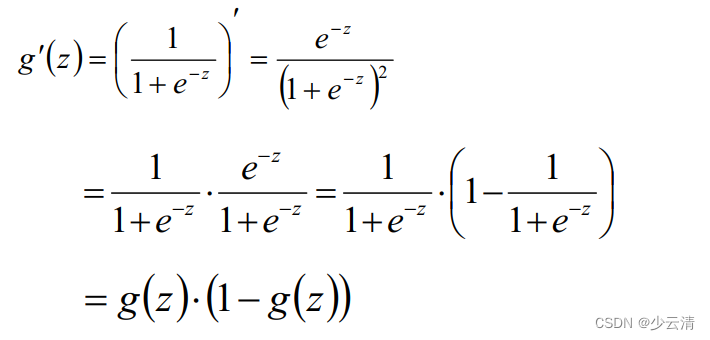
1.2 Logistic回归及似然函数(求解)
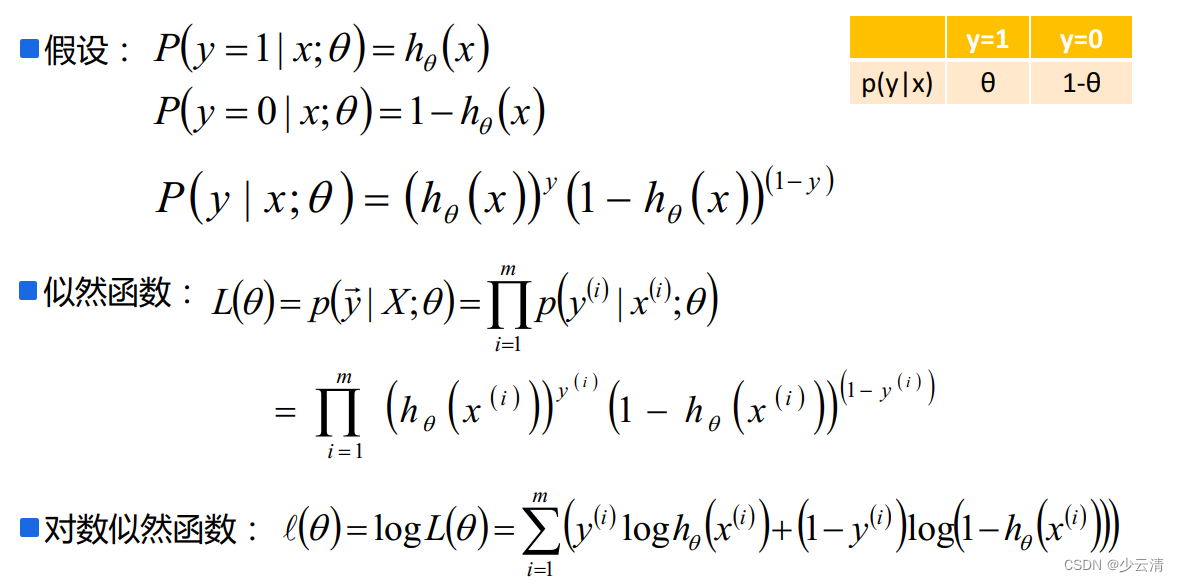
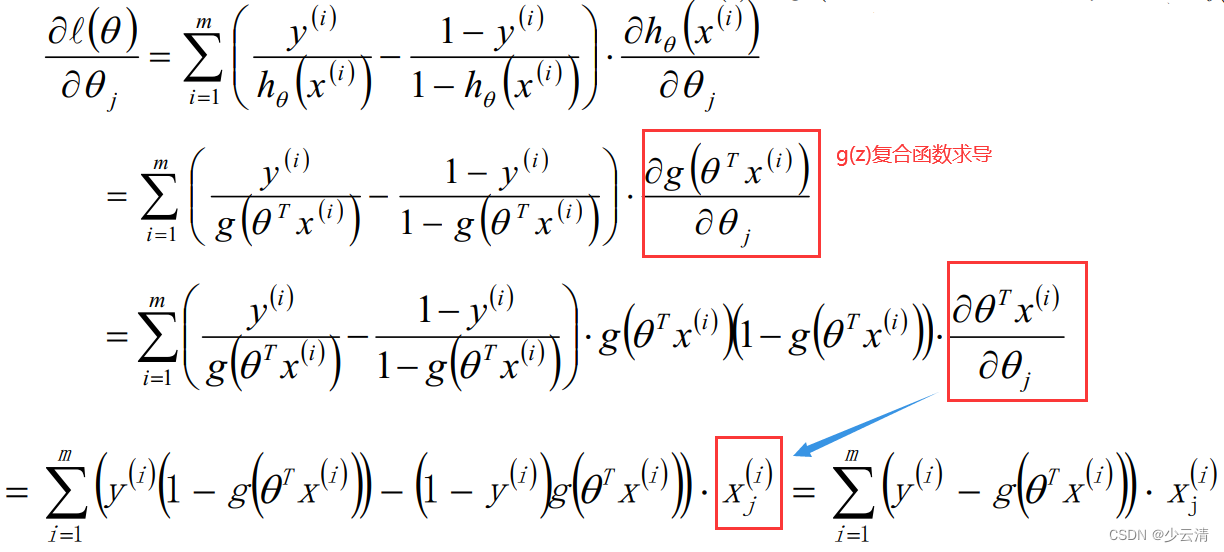
1.3 θ参数求解
Logistic回归θ参数的求解过程为(类似梯度下降方法):
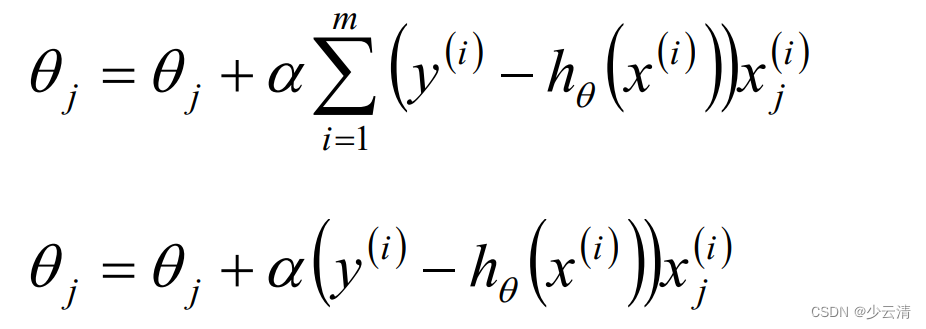
1.4 Logistic回归损失函数
与线性回归原理相同,但由于是分类问题,损失函数不一样,只能通过梯度下降求解
两种表示方式:
方法一:

方法二:(推荐)
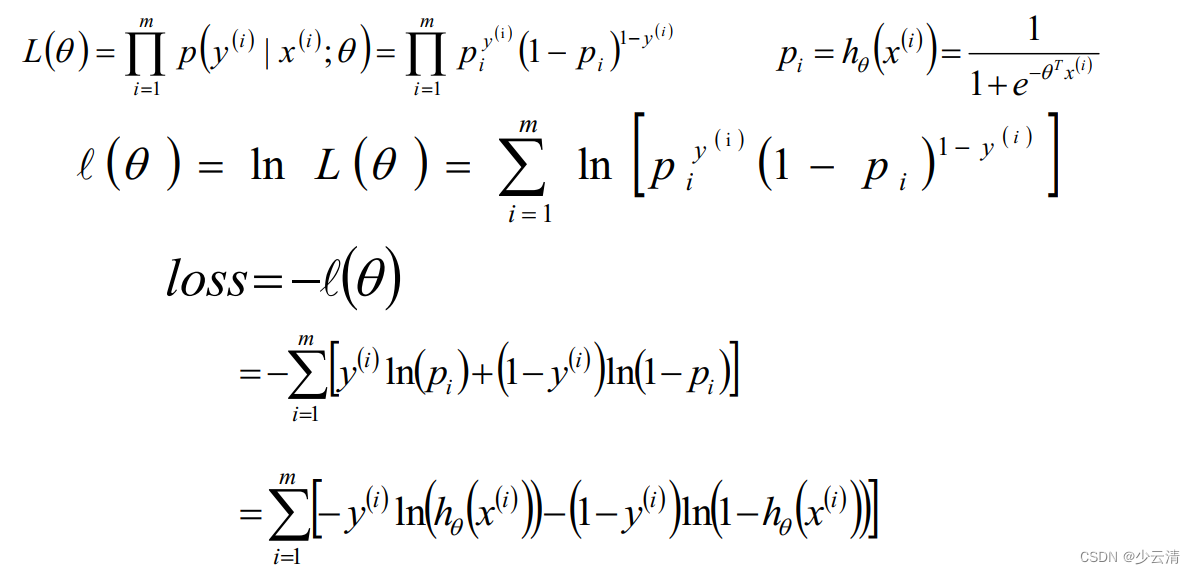
1.5 LogisticRegression总结
- 应用:广告点击率预测、电商购物搭配推荐
- 优点:适合需要得到一个分类概率的场景
- 缺点:当特征空间很大时,逻辑回归的性能不是很好(看硬件能力)
2 Softmax回归(多分类问题)
- softmax回归是logistic回归的一般化,适用于K分类的问题,第k类的参数为向量θk,组成的二维矩阵为θk*n
- softmax函数的本质就是将一个K维的任意实数向量压缩(映射)成另一个K维的实数向量,其中向量中的每个元素取值都介于(0,1)之间。
- softmax回归概率函数为:
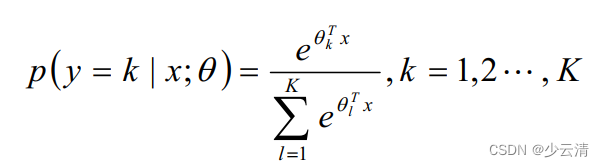
2.1 Softmax算法原理
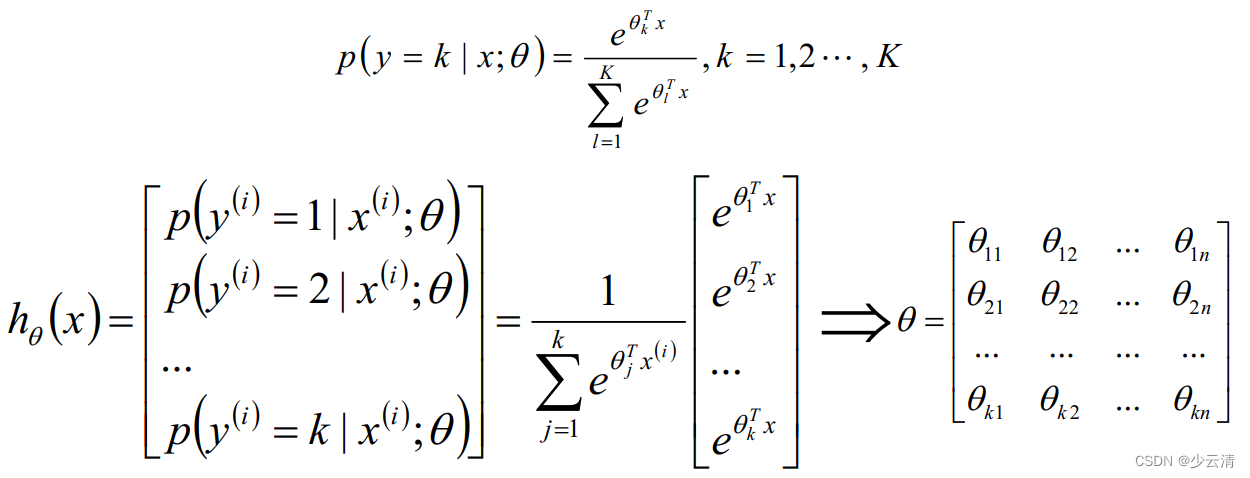
2.2 Softmax算法损失函数
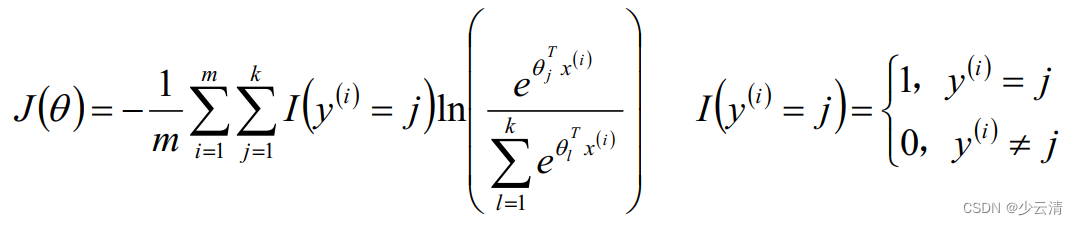
2.3 Softmax算法梯度下降法求解
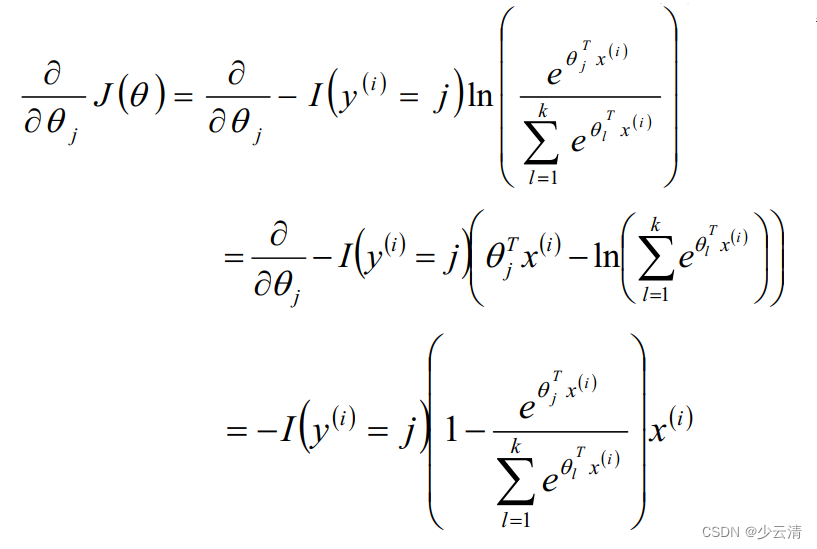
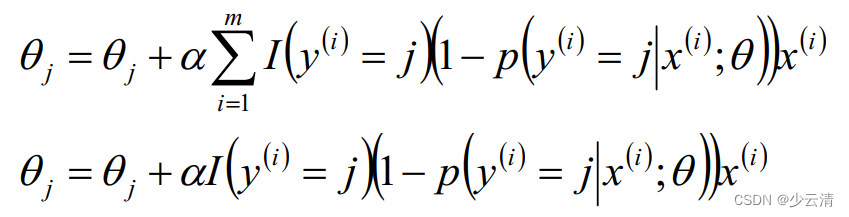
3 总结
- 线性模型一般用于回归问题,Logistic和Softmax模型一般用于分类问题
- 求θ的主要方式是梯度下降算法,梯度下降算法是参数优化的重要手段,主要是SGD,适用于在线学习以及跳出局部极小值
- Logistic/Softmax回归是实践中解决分类问题的最重要的方法
- 广义线性模型对样本要求不必要服从正态分布、只需要服从指数分布簇(二项分布、泊松分布、伯努利分布、指数分布等)即可;广义线性模型的自变量可以是连续的也可以是离散的。