题目描述
You have an array of elements
.
For each task, you have three integers .
Ask whether you can find an array of
integers satisfy:
are the multiplies of 2
Specially, if , it should satisfy
is the multiply of 2
We define .
If possible, print "YES". Otherwise, print "NO".
输入描述
Each test contains multiple test cases. The first line contains the number of test cases .
The description of the test cases follows.
The first line contains two integers .
The second line contains n� integers .
Each of the next lines contains three integers
.
It's guaranteed that
输出描述
For each test case, output "YES" or "NO".
样例
输入:
2
3 3
1 2 3
1 2 1
1 3 1
2 3 1
3 3
2 2 2
1 2 1
1 2 2
1 2 3输出:
NO
YES
NO
YES
YES
NO
题目大意:
给定一个区间,将这个区间划分为 段,每一段的和都要求是偶数,判断给定的区间能不能成功求出划分
思路:
可以先求解一个前缀和,根据前缀和判断一下。因为 这个区间的和要求是偶数(包含这两个端点),如果求出前
个数的和为奇数,那么前
个数的和也必须为奇数;如果前
个数是偶数,那个前
个数的和必须为偶数。
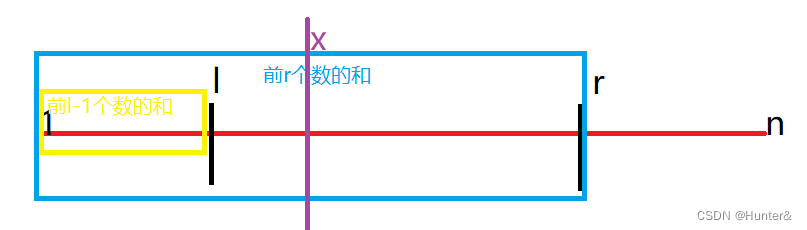
那么我们就可以知道,如果两个端点的前缀和是偶数,那个划分时间到x位置的前缀和也应该为偶数,如果两个端点的前缀和为奇数,那么到x位置的前缀和也应该为奇数。所以我们可以设置两个数据,分别来记录前缀和为奇数和前缀和为偶数的个数的前缀和。判断两边的端点是全奇还是全偶,求出区间最多可以划分为多少个,如果最多可以划分的个数小于需要划分的个数就是NO大于等于就是YES
代码:
#include<bits/stdc++.h>
using namespace std;const int N = 1e5 +7;using ll = long long;ll a[N], kcnt[N], vis[N],kcnt1[N];void solve() {vis[0] = 1;int n, q;cin >> n >> q;for(int i = 1; i <= n; i++) {cin >> a[i];kcnt[i] = 0;vis[i] = 0;}ll sum = 0;bool f = 0;for(int i = 1; i <= n; i++) {sum += a[i];if(sum % 2 == 0) {kcnt[i] = kcnt[i - 1] + 1;kcnt1[i] = kcnt1[i - 1];vis[i] = 1;}else {kcnt[i] = kcnt[i - 1];kcnt1[i] = kcnt1[i - 1] + 1;vis[i] = 0;}}
// for(int i = 0; i <= n; i++) {
// cout << kcnt[i] << ' ' << vis[i] << '\n';
// }while(q--) {int l, r, k;cin >> l >> r >> k;if(k > r - l + 1) {cout << "NO\n";continue;}if(vis[r] ^ vis[l - 1]) {cout << "NO\n";continue;}ll tk = kcnt[r] - kcnt[l - 1];if(!vis[l - 1]){tk = kcnt1[r] - kcnt1[l - 1];}if(tk >= k) {cout << "YES\n";}else {cout << "NO\n";}}
}int main() {ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);int T = 1;cin >> T;while(T--) {solve();}return 0;
}