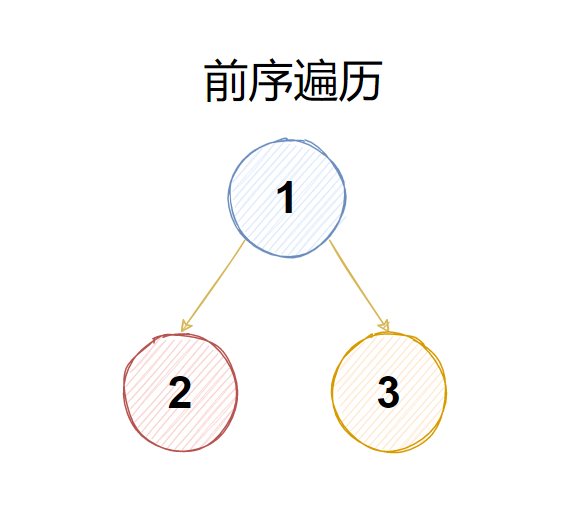
思路：

先把数组转化成一个对象（map），对象的key值是对象的id

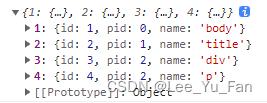
遍历对象；map[map[k].pid].children.push(map[k]),【k代表索引】，pid等于0代表是根节点

// 数结构转换let arr = [{id: 1,pid: 0,name: "body",},{id: 2,pid: 1,name: "title",},{id: 3,pid: 2,name: "div",},{id: 4,pid: 2,name: "p",},];function toTree(arr) {let result = [];let map = {};arr.forEach((item) => {map[item.id] = item;});console.log(map);for (let k in map) {if (map[k].pid == 0) {result.push(map[k]);} else {if (!map[map[k].pid].hasOwnProperty("children")) {map[map[k].pid].children = [];}map[map[k].pid].children.push(map[k]);}}console.log(result);}toTree(arr);

输出结果：