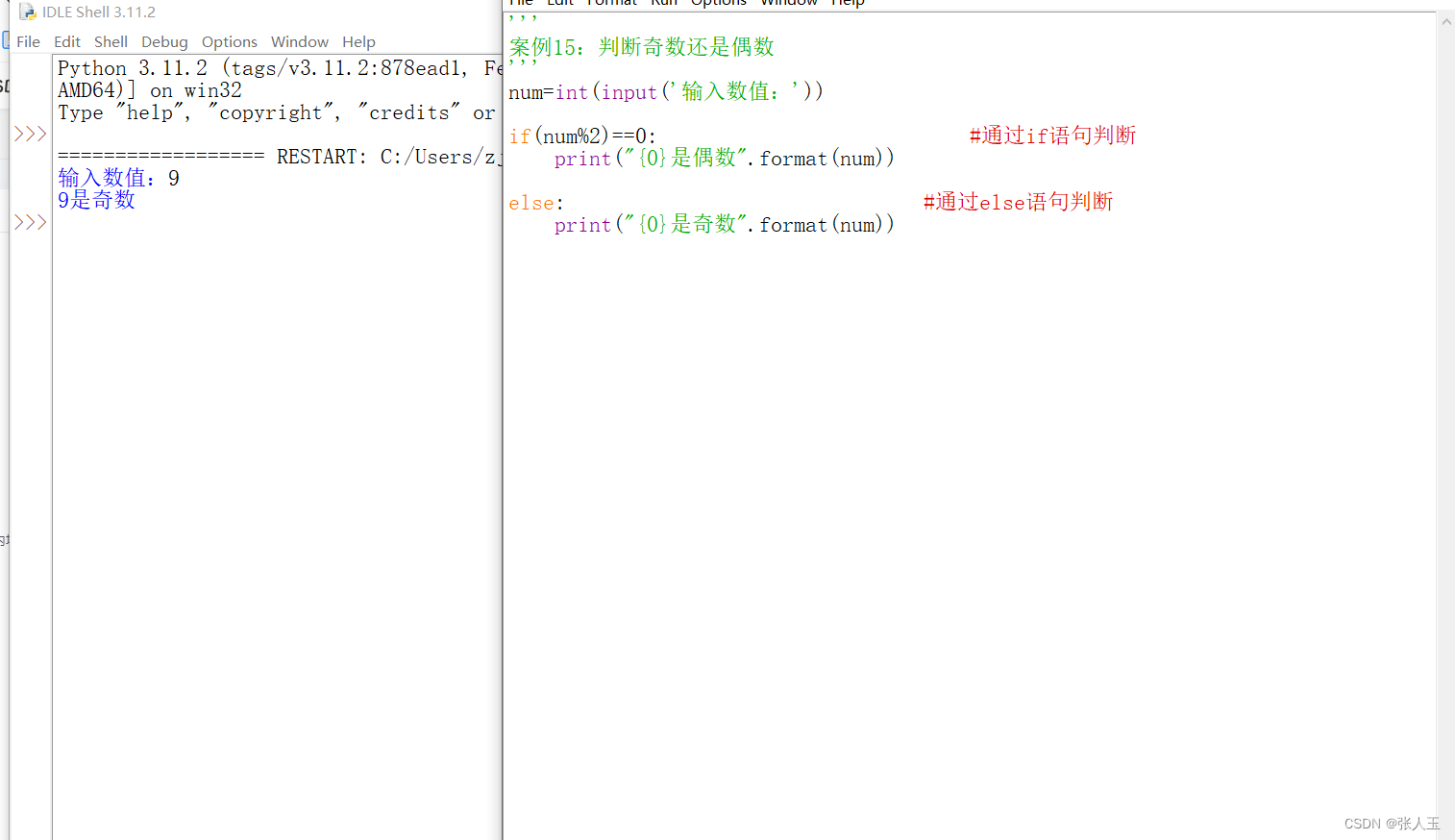
pdf怎么删除不要的页面？在处理pdf文档时，我们经常会遇到需要删除某些页面的情况。一些多余或无关的页面可能会对文档的整体结构造成混乱，甚至会影响文档的可读性。此外，删除多余页面还可以减小文件大小，方便存储和传输。下面就给大家介绍几种pdf删除页面的方法。

 

今天给大家介绍一款pdf转换工具，【迅捷PDF转换器】是一款功能强大的pdf处理工具，可以轻松地删除不需要的页面。它十分简单易用、使用起来也很快速高效。

在使用这款pdf转换工具的时候，需要先打开这款转换器，然后点击导入需要处理的pdf文档，然后选择“删除页面”选项，然后选择需要删除的页面范围，进行删除就可以了。

 

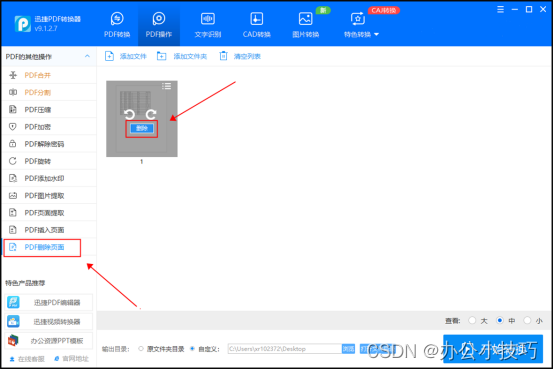
除了删除页面，这款转换器还提供了其他有用的pdf处理功能，如合并pdf文档、拆分pdf文档、添加水印等。它还支持批量处理，可以大大提高工作效率。

 

除了删除页面，如果你需要对pdf文档进行其他操作，例如合并或拆分文档，这款PDF转换器也可以满足你的需求。在使用的时候，你可以根据自己的需要选择不同的操作方式，来完成各种pdf处理任务。

 

pdf怎么删除不要的页面？如果您还没有使用过这款转换器，不妨下载试用一下。相信你会发现，使用这款转换器进行pdf页面删除等操作，非常方便快捷，可以帮助你节省大量的时间和精力，让你轻松完成各种pdf处理任务。