---

🚀一、分治法

⛳（一）算法思想

精炼：将一个难以直接解决的大问题，分割成一些规模较小的子问题，以便各个击破，分而治之。这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。

两部分组成

分（divide）：递归解决较小的问题
治（conquer）：然后从子问题的解构建原问题的解

三个步骤

1、分解（Divide）：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；
2、解决（Conquer）：若子问题规模较小而容易被解决则直接解决，否则递归地解各个子问题；
3、合并（Combine）：将各个子问题的解合并为原问题的解。

例子：

问：一个装有 16 枚硬币的袋子，16 枚硬币中有一个是伪造的，伪造的硬币和普通硬币从表面上看不出有任何差别，但是那 个伪造的硬币比真的硬币要轻。现有给你一台天平，请你在尽可能最短的时间内找出那枚伪造的硬币

1. 常规解决办法：

   每次拿出两枚硬币比重量，只到遇到两枚硬币重量不等时，重量更轻的那枚就是假币。这题这样比最多需要比8次，更多硬币就更耗时，时间复杂度位:O(n)

2. 分治思维解题：

   我们先将 16 枚硬币分为左右两个部分，各为 8 个硬币，分别称重，必然会有一半轻一半重，而我们要的就是轻的那组重的舍去。接下来我们继续对轻的进行五五分，直至每组剩下一枚或者两枚硬币，这时我们的问题自然就解决了。使用分治法此题需要比4次。**时间复杂度为:O(log2 n) ，**分治法的效率是可见的，如果基数加大效率提升将会大大提高。

⛳（二）相关代码

1、二分查找算法就使用了分而治之的思想：

#include <stdio.h>
#include <stdlib.h>/*递归实现二分查找
参数:
arr - 有序数组地址 arr
minSub - 查找范围的最小下标 minSub
maxSub - 查找范围的最大下标 maxSub
num - 带查找数字
返回:找到则返回所在数组下标，找不到则返回-1
*/int BinarySearch(int* arr,int minSub,int maxSub,int num){if(minSub>maxSub){return -1;//找不到 num 时,直接返回}int mid=(minSub+maxSub)/2;if(num<arr[mid]){return BinarySearch(arr,minSub,mid-1, num);  //递归找左边一半}else if(num>arr[mid]){return BinarySearch(arr,mid+1,maxSub, num);  //递归找右边一半}else{return mid;//找到 num 时直接返回}
}int main(void){int arr[]={1, 3, 7, 9, 11};int index = BinarySearch(arr, 0, 4, 8);printf("index: %d\n", index);system("pause");return 0;
}

2、如果机器人一次可以上 1 级台阶，也可以一次上 2 级台阶。求机器人走一个 n 级台阶总共有多少种走法。

分治法核心思想 ， 从上往下分析问题，大问题可以分解为子问题，子问题中还有更小的子问题：

• 比如总共有 5 级台阶,求有多少种走法；由于机器人一次可以走两级台阶，也可以走一级台阶，所以我们可以分成两个情况：

  机器人最后一次走了两级台阶，问题变成了“走上一个 3 级台阶，有多少种走法？”

  机器人最后一步走了一级台阶，问题变成了“走一个 4 级台阶，有多少种走法？”

• 我们将求 n 级台阶的共有多少种走法用 f(n) 来表示，则：

  f(n) = f(n-1) + f(n-2);

  由上可得 f(5) = f(4) + f(3);

  f(4) = f(3) + f(2);

  f(3)

/*递归实现机器人台阶走法统计 
参数:n - 台阶个数 
返回: 上台阶总的走法 */
int WalkCout(int n)
{ if(n<0) return 0; if(n==1) return 1; //一级台阶，一种走法 else if(n==2) return 2; //二级台阶，两种走法 else { //n 级台阶， n-1 个台阶走法 + n-2 个台阶的 走法 return WalkCout(n-1) + WalkCout(n-2); } 
}

总结：总体来讲，分治法思维较为简单，因为分解思维存在，常常需要使用递归、循环等，常见的使用分治法思维的问题有：合并排序、快速排序、汉诺塔问题、大整数乘法等。

🚀二、动态规划算法

⛳（一）算法思想

精炼：动态规划也是一种分治思想，但与分治算法不同的是，分治算法是把原问题分解为若干子问题，自顶向下，求解各子问题，合并子问题的解从而得到原问题的解。动态规划也是自顶向下把原问题分解为若干子问题，不同的是，之后自底向上，先求解最小的子问题，把结果存储在表格中，在求解大的子问题时，直接从表格中查询小的子问题的解，避免重复计算，从而提高算法效率。

1. 具体步骤：

   • 判题题意是否为找出一个问题的最优解
   • 从上往下分析问题，大问题可以分解为子问题，子问题中还有更小的子问题
   • 从下往上分析问题 ，找出这些问题之间的关联
   • 讨论底层的边界问题
   • 求解每个子问题仅一次，并将其结果保存在一个表中，以后用到时直接存取，不重复计算，节省计算时间，自底向上地计算。
   • 整体问题最优解取决于子问题的最优解（状态转移方程）（将子问题称为状态，最终状态的求解归结为其他状态的求解）

2. 什么时候要用动态规划：

   如果要求一个问题的最优解（通常是最大值或者最小值），而且该问题能够分解成若干个子问题，并且小问题之间也存在重叠的子问题，则考虑采用动态规划。

例子：

以动态规划中的机器人代码为例，是否发现上面的代码中存在很多重复的计算？比如：

比如: f(5) = f(4) + f(3)，计算分成两个分支：

f(4) = f(3)+f(2) = f(2) + f(1) + f(2);

f(3) = f(2) + f(1) ;

上面红色的部分就是重复计算的一部分！

⛳（二）相关代码

我们将机器人代码改为使用动态规划的思想：从下向上分析问题

f(1) = 1

f(2) = 2

f(3) = f(1) + f(2) = 3

f(4) = f(3) + f(2) = 3 + 2 = 5

f(5) = f(4) + f(3) = 5 + 3 = 8

。。。依次类推 。。。

#include <iostream>
#include <assert.h>
using namespace std;
/*
如果机器人 一次可以上 1 级台阶，也可以一次上 2 级台阶。
求机器人走一个 n 级台阶总共有多少种走法。
*///分治思想 
int GetSteps(int steps)
{assert(steps>0);if (1 == steps) return 1;if (2 == steps) return 2;return GetSteps(steps - 1)+ GetSteps(steps - 2);
}
//动态规划思想
int GetSteps2(int steps)
{assert(steps > 0);//由于台阶数从 1 开始计数，而数组索引从 0 开始计数，所以我们需要一个长度为 steps+1 的数组，以确保能够存储起始台阶到目标台阶的所有走法数。int *values=new int[steps+1]; //数组用于存储走steps个台阶的走法数values[1] = 1;values[2] = 2;for (int i=3;i<=steps;i++){values[i] = values[i - 1] + values[i - 2];}int n = values[steps];delete[] values;return n;
}

用分治思想的时间复杂度为：O(2^n)，空间复杂度为O(1)

用动态规划思想的时间复杂度为：O(n)，空间复杂度也为O(n)

🚀三、回溯算法

⛳（一）算法思想

**精炼：**回溯算法就是在问题的解空间中，按照某种方法（路径）去寻找问题的解，如果发现在当前情况继续往下已查不到解时，就“回溯”返回，尝试别的路径。

1、如果尝试求解的空间是一棵树：那么可以理解为

• 在问题的解空间中，按深度优先遍历策略，从根节点出发搜索解空间树。
• 算法搜索至解空间 的任意一个节点时，先判断该节点是否包含问题的解。如果确定不包含，跳过对以该节点为根的子树的搜索，逐层向其祖先节点回溯，否则进入该子树，继续深度优先搜索。
• 回溯法解问题的所有解时，必须回溯到根节点，且根节点的所有子树都被搜索后才结束。
• 回溯法解问题的一个解时，只要搜索到问题的一个解就可结束。

2、基本步骤

• 定义问题的解空间
• 确定易于搜索的解空间结构
• 以深度优先搜索的策略搜索解空间，并在搜索过程中尽可能避免无效搜索（将已经搜索过的结点做个标记）

⛳（二）相关代码

例子：

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了 矩阵的某一格，那么该路径不能再次进入该格子。例如在下面的 3×4 的矩阵中包含一条字符串 “bfce”的路径（路径中的字母用下划线标出）。但矩阵中不包含字符串“abfb”的路径，因为字符串的第一个字符 b 占据了矩阵中的第一行第二个格子之后，路径不能再次进入这个格子

解题思路：

• 首先，在矩阵中任选一个格子作为路径的起点。
• 如果路径上的第 i 个字符不是待搜索的目标字符 ch，那么这个格子不可能处在路径上的第 i 个位置。
• 如果路径上的第 i 个字符正好是 ch，那么往相邻的格子寻找路径上的第 i+1 个字符。除在矩阵边界上的格子之外，其他格子都有 4 个相邻的格子。
• 重复这个过程直到路径上的所有字符都在矩阵中找到相应的位置。
• 由于路径不能重复进入矩阵的格子，还需要定义和字符矩阵大小一样的布尔值矩阵，用来标识路径是否已经进入每个格子。
• 当矩阵中坐标为（row, col）的格子和路径字符串中相应的字符一样时，从 4 个相邻的格子(row,col-1),(row-1,col),(row,col+1)以及(row+1,col)中去定位路径字符串中下一个字符, 如果 4 个相邻的格子都没有匹配字符串中下一个的字符，表明当前路径字符串中字符在矩阵中的定位不正确，我们需要回到前一个，然后重新定位。

#include <iostream>
#include<assert.h>
using namespace std;/*
名企面试题： 请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。
路径可以 从矩阵中任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。
如果一条路径经过了 矩阵的某一格，那么该路径不能再次进入该格子。
例如在下面的 3×4 的矩阵中包含一条字符串 “bfce”的路径（路径中的字母用下划线标出）。
但矩阵中不包含字符串“abfb”的路径，因为 字符串的第一个字符 b 占据了矩阵中的第一行第二个格子之后，
路径不能再次进入这个格子。 
A B T G
C F C S
J D E H
*//*探测一个字符是否存在*/
bool isEqualSimpleStr(const char *matrix, int rows, int cols, int row, int col, int &strlength, const char * str,bool *visited);/*
功能: 判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。
参数:
@ 矩阵 
@ 矩阵行数
@ 矩阵列数
@ 待查字符串
返回值：如果矩阵中存在 str 则返回 true ，否则返回 false
*/
bool IsHasStr(const char *matrix, int rows, int cols, const char *str)
{if (matrix == nullptr || rows < 1 || cols < 1 || str == nullptr) return false;int strLength = 0;bool *visited = new bool[rows*cols];memset(visited, 0, rows * cols);for (int row=0;row<rows;row++)for(int col=0;col<cols;col++){if (isEqualSimpleStr( matrix, rows, cols, row, col, strLength,str,visited)){//delete [] visited;return true;}}delete [] visited;return false;
}bool isEqualSimpleStr(const char *matrix, int rows, int cols, int row, int col, int &strlength, const char * str, bool *visited)
{if (str[strlength] == '\0') return true;//如果找到了字符串的结尾 则代表矩阵中存在该字符串路径bool isEqual = false;if (row>=0&&row<rows && col>=0&&col<cols&& visited[row*cols+col]==false&& matrix[row*cols+col]==str[strlength]){strlength++;visited[row*cols + col] == true;isEqual = isEqualSimpleStr(matrix, rows, cols, row, col - 1, strlength, str, visited)|| isEqualSimpleStr(matrix, rows, cols, row, col + 1, strlength, str, visited)|| isEqualSimpleStr(matrix, rows, cols, row - 1, col, strlength, str, visited)|| isEqualSimpleStr(matrix, rows, cols, row + 1, col, strlength, str, visited);if (!isEqual) //如果没找到{strlength--;visited[row*cols + col] == false;}	}return isEqual;
}int main()
{const char* matrix = "ABTG""CFCS""JDEH";const char* str = "BFCE";bool isExist = IsHasStr((const char*)matrix, 3, 4, str);if (isExist)cout << "matrix中存在 " << str << " 字符串的路径" << endl;elsecout << "matrix中不存在 " << str << " 字符串的路径" << endl;
}

回溯算法常常用在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。

🚀四、贪心算法

⛳（一）算法思想

精炼：（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解

基本步骤：

• 建立数学模型来描述问题
• 把求解的问题分成若干个子问题
• 对每一子问题求解，得到子问题的局部最优解
• 把子问题对应的局部最优解合成原来整个问题的一个近似最优解

⛳（二）相关代码

假设 1元、2元、5元、10元、50元、100元的纸币分别有c0，c1，c2，c3，c4，c5，c6张，现在要用这些钱来支付K元，至少要用多少张纸币？

解题思路：

用贪心算法的思想，很显然，每一步尽可能用面值大的纸币即可。在日常生活中我们自然而然也是这么做的。在程序中已经事先将Value按照从小到大的顺序排好

#include<iostream>
using namespace std;
/*
假设 1元、2元、5元、10元、50元、100元的纸币分别有c0，c1，c2，c3，c4，c5，c6张
现在要用这些钱来支付K元，至少要用多少张纸币
*/int money_Type_Count[6][2] = { {1,20},{2,5},{5,10},{10,2},{50,2},{100,3} };
/*
功能:获取支付这些钱需要纸币的张数
参数： @金额
返回值：返回需要纸币的张数，如果找不开返回-1
*/
int getPaperNums(int Money)
{int num = 0;for (int i=5;i>=0;i--){int tmp = Money / money_Type_Count[i][0];tmp = tmp > money_Type_Count[i][1] ? money_Type_Count[i][1] : tmp;cout << "给你 " << money_Type_Count[i][0] << " 的纸币" << tmp << " 张" << endl;num += tmp;Money -= tmp * money_Type_Count[i][0];}if (Money > 0) return -1;return num;
}int main()
{int money;cout << "请输入金额:" << endl;;cin >> money;int num = getPaperNums(money);if (num == -1){cout << "抱歉，你的钱不够" << endl;}else{cout << "一共给了 " << num << " 张纸币" << endl;}
}

贪心策略适用的前提是：局部最优策略能导致产生全局最优解。对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解。

🚀五、分支定界法

⛳（一）算法思想

**精炼：**和回溯法一样，也是一种在问题的解空间上搜索问题的解的方法。但与回溯算法不同，分支定界算法采用广度优先或最小耗费优先的方法搜索解空间树，并且，在分支定界算法中，每一个活结点只有一次机会成为扩展结点。

1、算法步骤：

1. 产生当前扩展结点的所有孩子结点；
2. 在产生的孩子结点中，抛弃那些不可能产生可行解（或最优解）的结点；
3. 将其余的孩子结点加入活结点表；
4. 从活结点表中选择下一个活结点作为新的扩展结点。

如此循环，直到找到问题的可行解（最优解）或活结点表为空。

2、从活结点表中选择下一个活结点作为新的扩展结点，根据选择方式的不同，分支定界算法通常可以分为两种形式：

• FIFO(First In First Out) 分支定界算法：按照先进先出原则选择下一个活结点作为扩展结点，即从活结点表中取出结点的顺序与加入结点的顺序相同。（广度优先的方式）
• 最小耗费或最大收益分支定界算法：在这种情况下，每个结点都有一个耗费或收益。假如要查找一个具有最小耗费的解，那么要选择的下一个扩展结点就是活结点表中具有最小耗费的活结点；假如要查找一个具有最大收益的解，那么要选择的下一个扩展结点就是活结点表中具有最大收益的活结点。（最小耗费优先的方式：A*算法）

⛳（二）相关代码

布线问题：

• 印刷电路板将布线区域划分成n*m个方格阵列。
• 精确的电路布线问题要求确定连接方格a的中点到方格b的中点的最短布线方案。
• 在布线时，电路只能沿直线或直角布线。
• 为了避免线路相交，已布了线的方格做了封锁标记，其他线路不允许穿过被封锁的方格。

解题思路：

回溯法：

回溯法的搜索是依据深度优先的原则进行的，如果我们把上下左右四个方向规定一个固定的优先顺序去进行搜索，搜索会沿着某个路径一直进行下去直到碰壁才换到另一个子路径，但是我们最开始根本无法判断正确的路径方向是什么，这就造成了搜索的盲目和浪费。

分支定界法：

采用广度优先的方式，过程：

• 从起始位置a开始将它作为第一个扩展结点
• 与该结点相邻并且可达的方格被加入到活缓点队列中，并且将这些方格标记为1
• 接着从活结点队列中取出队首作为下一个扩展结点，并将与当前扩展结点相邻且未标记过的方格标记为2，并存入活节点队列
• 这个过程一直继续到算法搜索到目标方格b或活结点队列为空时为止(表示没有通路)

1、定义小方格位置

定义一个表示电路板上小方格位置的类Position,它的两个私有成员row和col分别表示小方格所在的行和列。

在电路板的任何一个方格处，布线可沿右、下、左、上4个方向进行。沿这4个方向的移动分别记为0,1，2，3。沿着这4个方向前进一步相对于当前方格的位移如下表所示。

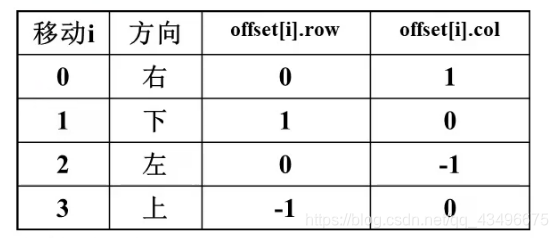
2、实现方格阵列

用二维数组grid表示所给的方格阵列。初始时，grid[i][j]=0，表示该方格允许布线，而grid[i][j]=1表示该方格被封锁，不允许布线。

为了便于处理方格边界的情况，算法在所给方格阵列四周设置一圈标记为“1”的附加方格，即可识别方阵边界。

3、初始化

算法开始时，测试初始方格与目标方格是否相同。如果相同，则不必计算，直接放回最短距离0，否则算法设置方格阵列的边界，初始化位移矩阵offset。

4、算法搜索步骤

算法从start开始，标记所有标记距离为1的方格并存入活结点队列，然后依次标记所有标记距离为2,3…的方格，直到到达目标方格finish或活结点队列为空时为止

/*
布线问题：如图1所示，印刷电路板将布线区域划分成n*m个方格。
精确的电路布线问题要求确定连接方格a的中点到b的中点的布线方案。
在布线时，电路只能沿直线或直角布线，
所示。为了避免线路相交，已经布线的方格做了封锁标记（如图1中阴影部分）
，其他线路不允许穿过被封锁的方格。
*/#include <iostream>
#include <queue>
#include <list>
using namespace std;
typedef struct _Pos
{int x, y;struct _Pos* parent;
}Pos;int Move[4][2] = { 0,1,0,-1,-1,0,1,0 };
queue<Pos*> bound;void inBound(int x,int y,int rows,int cols, Pos * cur,bool *visited,int *map);Pos *Findpath(int *map,Pos start, Pos end,int rows,int cols)
{Pos *tmp = new Pos;tmp->x = start.x;tmp->y = start.y;tmp->parent = NULL;if (tmp->x == end.x && tmp->y == end.y &&tmp->y == end.y)return tmp;bool *visited = new bool[rows*cols];memset(visited, 0, rows*cols);visited[tmp->x*rows + tmp->y] = true;inBound(tmp->x, tmp->y, rows, cols,tmp,visited,map);while (!bound.empty()){Pos * cur = bound.front();if (cur->x == end.x && cur->y == end.y)return cur;bound.pop();inBound(cur->x, cur->y, rows, cols, cur,visited,map);}return NULL;//代表没有路径
}
void inBound(int x, int y, int rows, int cols,Pos*cur,bool *visited, int *map)
{for (int i = 0; i < 4; i++){Pos *tmp = new Pos;tmp->x = x + Move[i][0];tmp->y = y + Move[i][1];tmp->parent = cur;if (tmp->x >= 0 && tmp->x < rows && tmp->y >= 0 && tmp->y < cols && !visited[tmp->x*rows + tmp->y] && map[tmp->x*rows + tmp->y]!=1){bound.push(tmp);visited[tmp->x*rows + tmp->y] = true;}	elsedelete tmp;}
}list<Pos *> getPath(int *map, Pos start, Pos end, int rows, int cols)
{list<Pos*> tmp;Pos * result = Findpath(map, start, end, rows, cols);while (result!=NULL && result->parent!=NULL){tmp.push_front(result);result = result->parent;}return tmp;
}int main()
{int map[6][6] ={0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0 };Pos start = { 1,1,0 };Pos end = { 4,4,0 };list<Pos*> path = getPath(&map[0][0], start,end,6, 6);cout << "路径为:" << endl;for (list<Pos*>::const_iterator it=path.begin();it!=path.end();it++){cout << "(" << (*it)->x << "," << (*it)->y << ")" << endl;}system("pause");}