定义

逆波兰表达式也称为“后缀表达式”，是将运算符写在操作数之后的运算式。

求法

*如：(a+b)c-(a+b)/e的转换过程：

1. 先加上所有的括号。
   (((a+b)*c)-((a+b)/e))
2. 将所有的运算符移到括号外面
   (((ab)+ c)* ((ab)+ e)/)-
3. 去掉所有的括号
   ab + c * ab + e /-

所以最终的结果：ab + c * ab + e /-

代码思想：

使用栈这种数据结构进行计算。

1. 定义一个下标i进行遍历整个字符串
   
2. 只要不是运算符，那就将操作数入栈。
   
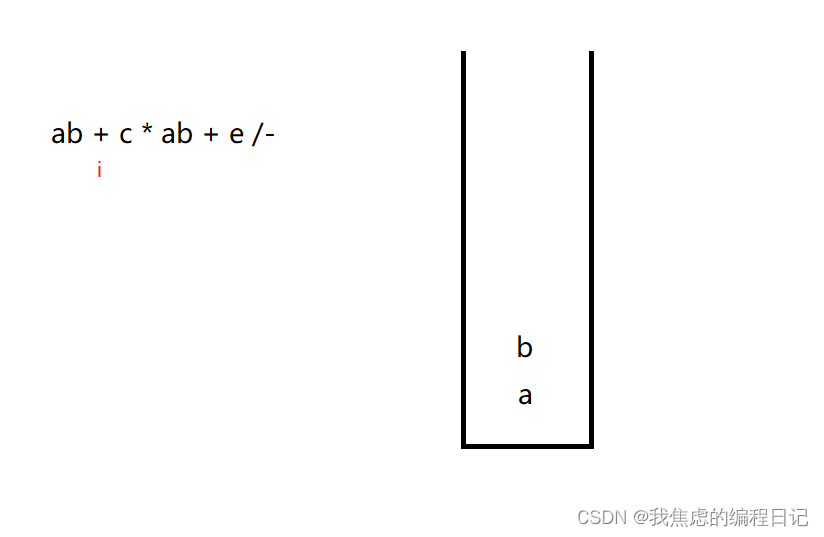
3. 当遇到操作符，从栈中弹出两个数进行计算，将结果入栈。同时下标i继续向后遍历。
   
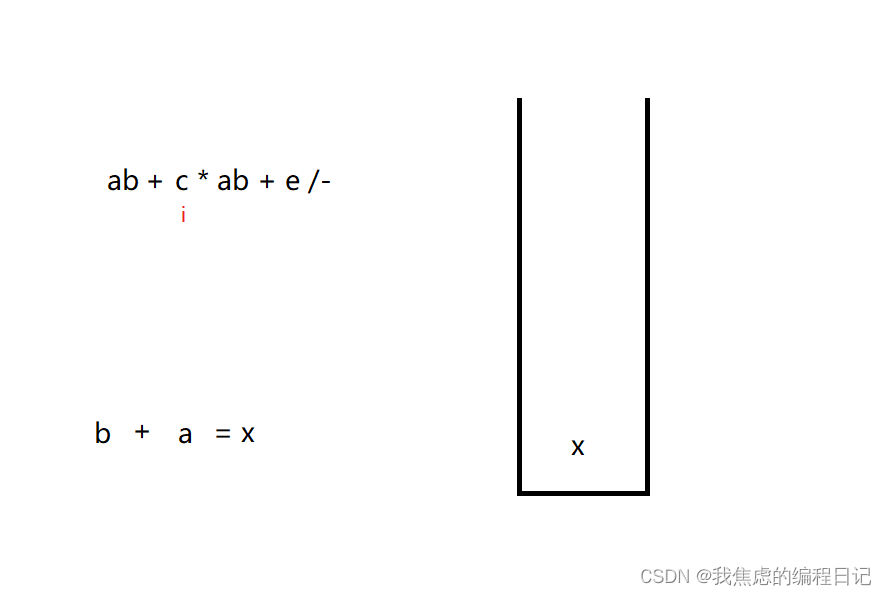
4. 重复上述过程。
   

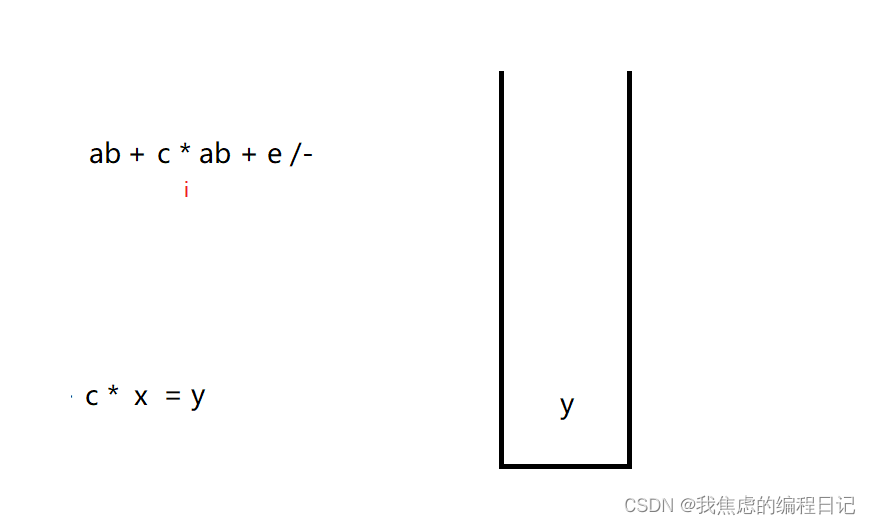
向后遍历至运算符：

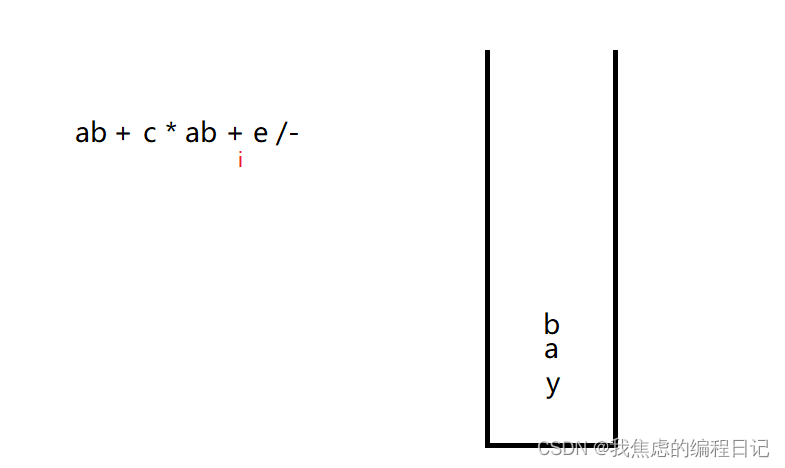
进行运算，并将结果进行入栈：

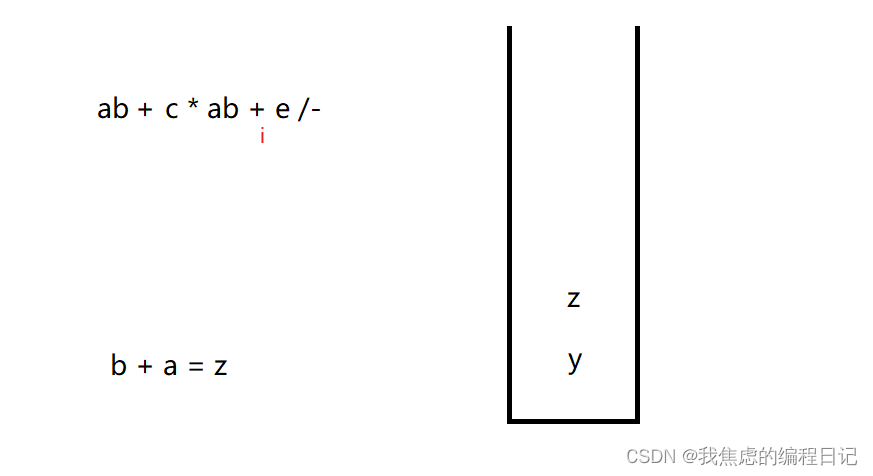
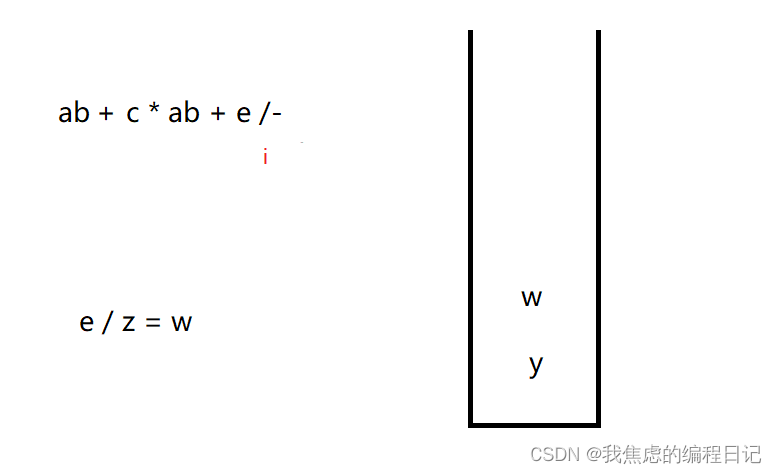
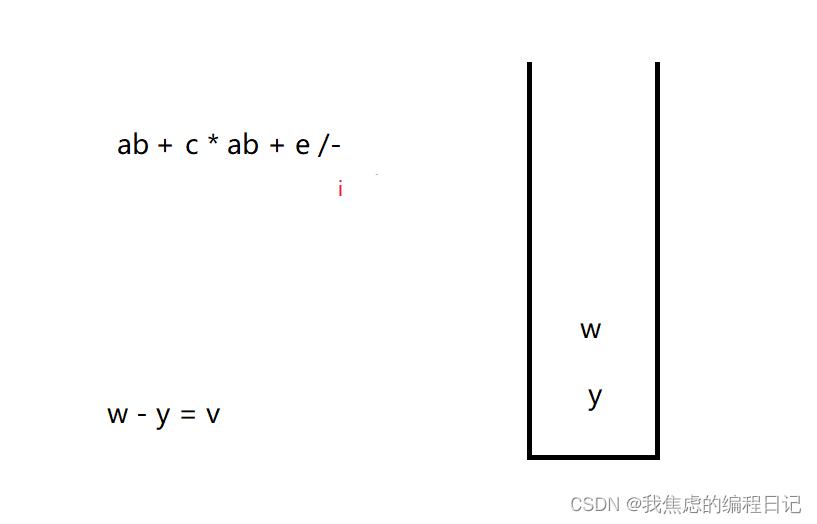
各步运算结果：

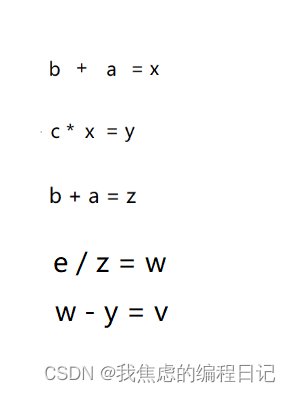
代码：

class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for (int i = 0; i < tokens.length; i++) {// 将数字入栈等待运算if (!(tokens[i].equals("+")|| tokens[i].equals("-")|| tokens[i].equals("*")|| tokens[i].equals("/"))) {stack.push(Integer.parseInt(tokens[i]));}// 如果是运算符，弹出两个数字进行运算else {int num1 = stack.pop();int num2 = stack.pop();int res = 0;// 进行运算switch (tokens[i]) {case "+":res = num2 + num1;break;case "-":res = num2 - num1;break;case "*":res = num2 * num1;break;case "/":res = num2 / num1;break;default:break;}// 将结果入栈stack.push(res);}}return stack.peek();}
}