RSI指数的计算非常简单，就是使用一段时间内的平均上涨除以平均上涨加平均下跌（取正值）。也就意味着RSI指数的取值是[0,100]之间，其中0表示周期内没有上涨的，100表示周期内没有下跌的。RSI的直观意义是它表示了一段周期内的上涨力占总量的比例，值越高上涨力越强。超过70表示的是进入了超买阶段、低于30表示进入超卖阶段。

撑压线对于RSI指数也是适用的，如下：

黄色的 线是6日的RSI指数，可见目前已经跌破支撑线，且超过超卖阶段。再来看成交量：

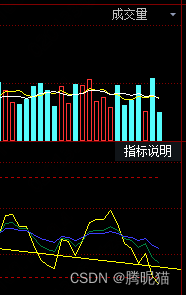
可见之前一日的成交量略大于之前下跌的成交量，这个是符合头肩底图形规则的，今天半日的成交量观察应该会超过上一个下跌的第二阶段的下跌，但是由于已经是超卖状态，其维持下跌趋势的可能性较低，因此不太可能形成头肩底，目前观察这是一个错误的信号，近期内不太可能形成强势的上涨状态。