2.4_数理统计的基本概念
数理统计思维导图
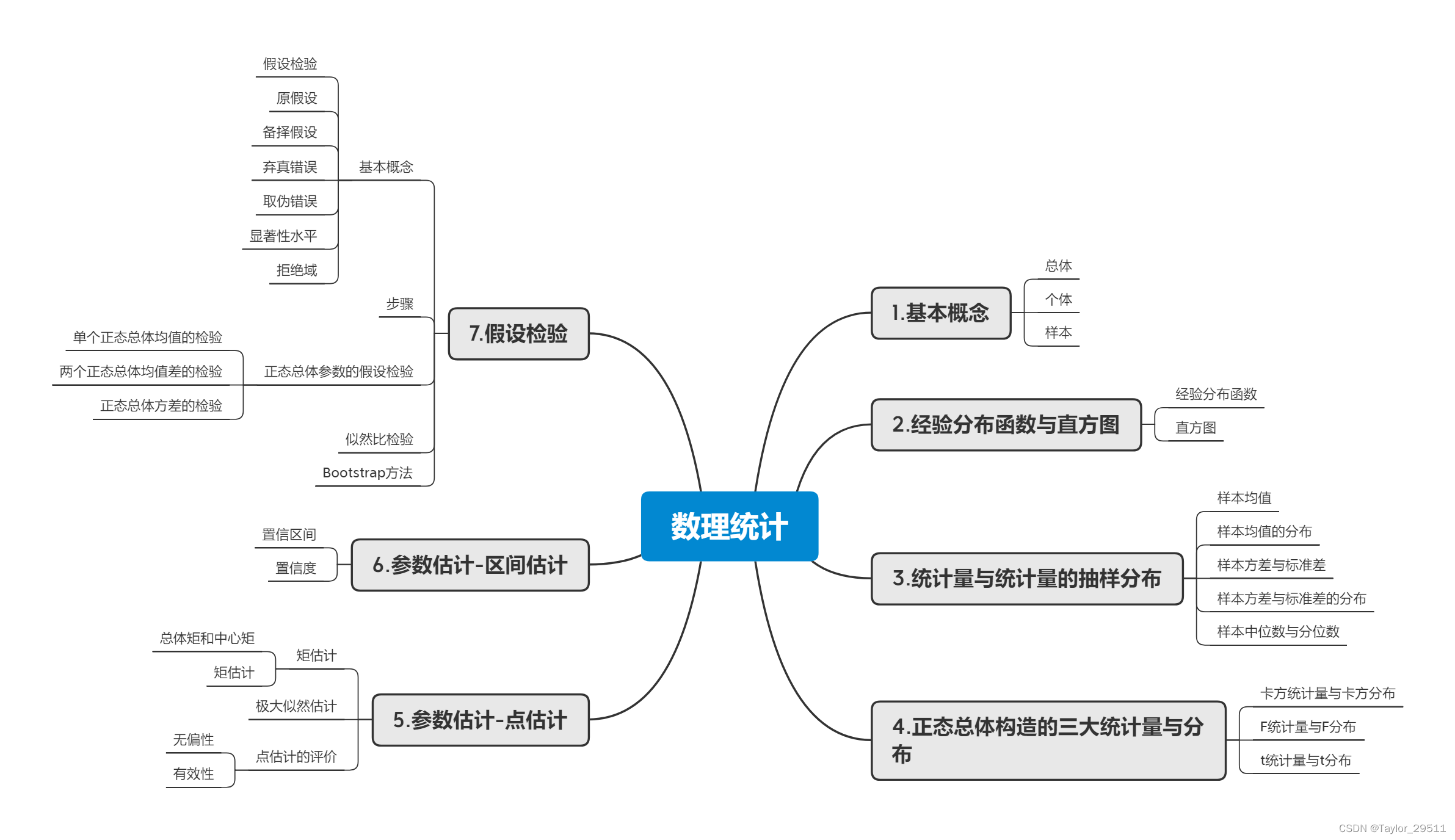
更多详细内容见notebook
1.基本概念
总体:研究对象的全体,它是一个随机变量,用 X X X表示。
个体:组成总体的每个基本元素。
简单随机样本:来自总体 X X X的 n n n个相互独立且与总体同分布的随机变量 X 1 , X 2 ⋯ , X n X_{1},X_{2}\cdots,X_{n} X1,X2⋯,Xn,称为容量为 n n n的简单随机样本,简称样本。
统计量:设 X 1 , X 2 ⋯ , X n , X_{1},X_{2}\cdots,X_{n}, X1,X2⋯,Xn,是来自总体 X X X的一个样本, g ( X 1 , X 2 ⋯ , X n ) g(X_{1},X_{2}\cdots,X_{n}) g(X1,X2⋯,Xn))是样本的连续函数,且 g ( ) g() g()中不含任何未知参数,则称 g ( X 1 , X 2 ⋯ , X n ) g(X_{1},X_{2}\cdots,X_{n}) g(X1,X2⋯,Xn)为统计量。
样本均值:
X ‾ = 1 n ∑ i = 1 n X i \overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i} X=n1∑i=1nXi
样本方差: S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 S^{2} = \frac{1}{n - 1}\sum_{i = 1}^{n}{(X_{i} - \overline{X})}^{2} S2=n−11∑i=1n(Xi−X)2
样本矩:样本 k k k阶原点矩: A k = 1 n ∑ i = 1 n X i k , k = 1 , 2 , ⋯ A_{k} = \frac{1}{n}\sum_{i = 1}^{n}X_{i}^{k},k = 1,2,\cdots Ak=n1∑i=1nXik,k=1,2,⋯
样本 k k k阶中心矩: B k = 1 n ∑ i = 1 n ( X i − X ‾ ) k , k = 1 , 2 , ⋯ B_{k} = \frac{1}{n}\sum_{i = 1}^{n}{(X_{i} - \overline{X})}^{k},k = 1,2,\cdots Bk=n1∑i=1n(Xi−X)k,k=1,2,⋯
2.分布
χ 2 \chi^{2} χ2分布: χ 2 = X 1 2 + X 2 2 + ⋯ + X n 2 ∼ χ 2 ( n ) \chi^{2} = X_{1}^{2} + X_{2}^{2} + \cdots + X_{n}^{2}\sim\chi^{2}(n) χ2=X12+X22+⋯+Xn2∼χ2(n),其中 X 1 , X 2 ⋯ , X n , X_{1},X_{2}\cdots,X_{n}, X1,X2⋯,Xn,相互独立,且同服从 N ( 0 , 1 ) N(0,1) N(0,1)
t t t分布: T = X Y / n ∼ t ( n ) T = \frac{X}{\sqrt{Y/n}}\sim t(n) T=Y/nX∼t(n) ,其中 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) , X\sim N\left( 0,1 \right),Y\sim\chi^{2}(n), X∼N(0,1),Y∼χ2(n),且 X X X, Y Y Y 相互独立。
F F F分布: F = X / n 1 Y / n 2 ∼ F ( n 1 , n 2 ) F = \frac{X/n_{1}}{Y/n_{2}}\sim F(n_{1},n_{2}) F=Y/n2X/n1∼F(n1,n2),其中 X ∼ χ 2 ( n 1 ) , Y ∼ χ 2 ( n 2 ) , X\sim\chi^{2}\left( n_{1} \right),Y\sim\chi^{2}(n_{2}), X∼χ2(n1),Y∼χ2(n2),且 X X X, Y Y Y相互独立。
分位数:若 P ( X ≤ x α ) = α , P(X \leq x_{\alpha}) = \alpha, P(X≤xα)=α,则称 x α x_{\alpha} xα为 X X X的 α \alpha α分位数
3.正态总体的常用样本分布
设 X 1 , X 2 ⋯ , X n X_{1},X_{2}\cdots,X_{n} X1,X2⋯,Xn为来自正态总体 N ( μ , σ 2 ) N(\mu,\sigma^{2}) N(μ,σ2)的样本, X ‾ = 1 n ∑ i = 1 n X i , S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 , \overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i},S^{2} = \frac{1}{n - 1}\sum_{i = 1}^{n}{{(X_{i} - \overline{X})}^{2},} X=n1∑i=1nXi,S2=n−11∑i=1n(Xi−X)2,则:
(1) X ‾ ∼ N ( μ , σ 2 n ) \overline{X}\sim N\left( \mu,\frac{\sigma^{2}}{n} \right){\ \ } X∼N(μ,nσ2) 或者 X ‾ − μ σ n ∼ N ( 0 , 1 ) \frac{\overline{X} - \mu}{\frac{\sigma}{\sqrt{n}}}\sim N(0,1) nσX−μ∼N(0,1)
(2) ( n − 1 ) S 2 σ 2 = 1 σ 2 ∑ i = 1 n ( X i − X ‾ ) 2 ∼ χ 2 ( n − 1 ) \frac{(n - 1)S^{2}}{\sigma^{2}} = \frac{1}{\sigma^{2}}\sum_{i = 1}^{n}{{(X_{i} - \overline{X})}^{2}\sim\chi^{2}(n - 1)} σ2(n−1)S2=σ21∑i=1n(Xi−X)2∼χ2(n−1)
(3) 1 σ 2 ∑ i = 1 n ( X i − μ ) 2 ∼ χ 2 ( n ) \frac{1}{\sigma^{2}}\sum_{i = 1}^{n}{{(X_{i} - \mu)}^{2}\sim\chi^{2}(n)} σ21∑i=1n(Xi−μ)2∼χ2(n)
(4) X ‾ − μ S / n ∼ t ( n − 1 ) {\ \ }\frac{\overline{X} - \mu}{S/\sqrt{n}}\sim t(n - 1) S/nX−μ∼t(n−1)
4.重要公式与结论
(1) 对于 χ 2 ∼ χ 2 ( n ) \chi^{2}\sim\chi^{2}(n) χ2∼χ2(n),有 E ( χ 2 ( n ) ) = n , D ( χ 2 ( n ) ) = 2 n ; E(\chi^{2}(n)) = n,D(\chi^{2}(n)) = 2n; E(χ2(n))=n,D(χ2(n))=2n;
(2) 对于 T ∼ t ( n ) T\sim t(n) T∼t(n),有 E ( T ) = 0 , D ( T ) = n n − 2 ( n > 2 ) E(T) = 0,D(T) = \frac{n}{n - 2}(n > 2) E(T)=0,D(T)=n−2n(n>2);
(3) 对于 F ~ F ( m , n ) F\tilde{\ }F(m,n) F ~F(m,n),有 1 F ∼ F ( n , m ) , F a / 2 ( m , n ) = 1 F 1 − a / 2 ( n , m ) ; \frac{1}{F}\sim F(n,m),F_{a/2}(m,n) = \frac{1}{F_{1 - a/2}(n,m)}; F1∼F(n,m),Fa/2(m,n)=F1−a/2(n,m)1;
(4) 对于任意总体 X X X,有 E ( X ‾ ) = E ( X ) , E ( S 2 ) = D ( X ) , D ( X ‾ ) = D ( X ) n E(\overline{X}) = E(X),E(S^{2}) = D(X),D(\overline{X}) = \frac{D(X)}{n} E(X)=E(X),E(S2)=D(X),D(X)=nD(X)