【力扣周赛】第 358 场周赛

文章目录

  • 竞赛链接
  • Q1：6939. 数组中的最大数对和
  • Q2：6914. 翻倍以链表形式表示的数字
    • 竞赛时代码——存入列表再计算
    • 解法2——只有下一个节点大于 4 的时候，才会因为进位多加一
  • Q3：7022. 限制条件下元素之间的最小绝对差
    • 竞赛时代码——手写二分
    • 写法2——使用API（TreeSet）
  • Q4：7023. 操作使得分最大（大杂烩：数学 + 单调栈(贡献法) + 贪心）
    • 竞赛时代码
    • 相关子题目
      • 质因数分解
        • 求质因数分解
        • 求质因数的数量
      • 快速幂
  • 成绩记录

竞赛链接

https://leetcode.cn/contest/weekly-contest-358/

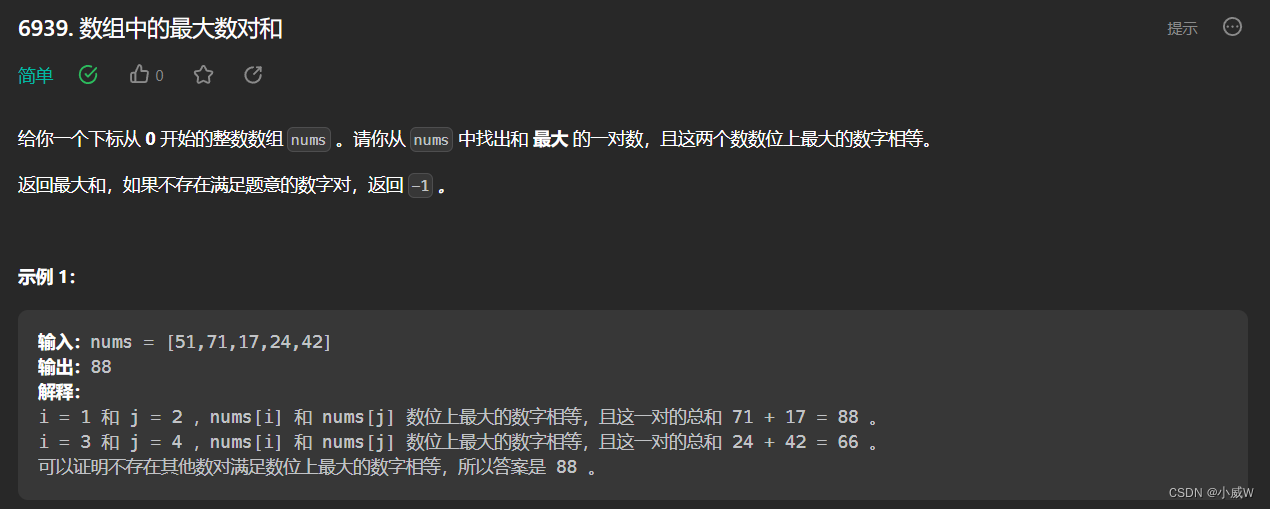
Q1：6939. 数组中的最大数对和

https://leetcode.cn/problems/max-pair-sum-in-an-array/

在这里插入图片描述
提示：

2 <= nums.length <= 100
1 <= nums[i] <= 10^4

竞赛时代码—— O ( n 2 ) O(n^2) O(n2)

class Solution {public int maxSum(int[] nums) {int ans = -1, n = nums.length;for (int i = 0; i < n; ++i) {for (int j = i + 1; j < n; ++j) {if (op(nums[i]) == op(nums[j])) {ans = Math.max(ans, nums[i] + nums[j]);}}}return ans;}public int op(int n) {int res = -1;while (n != 0) {res = Math.max(res, n % 10);n /= 10;}return res;}
}

解法2——一次遍历 O ( n ) O(n) O(n)，维护最大数位为 i 的元素的最大值

https://leetcode.cn/problems/max-pair-sum-in-an-array/solutions/2385996/yi-ci-bian-li-by-endlesscheng-6zt9/

在这里插入代码片

Q2：6914. 翻倍以链表形式表示的数字

https://leetcode.cn/problems/double-a-number-represented-as-a-linked-list/

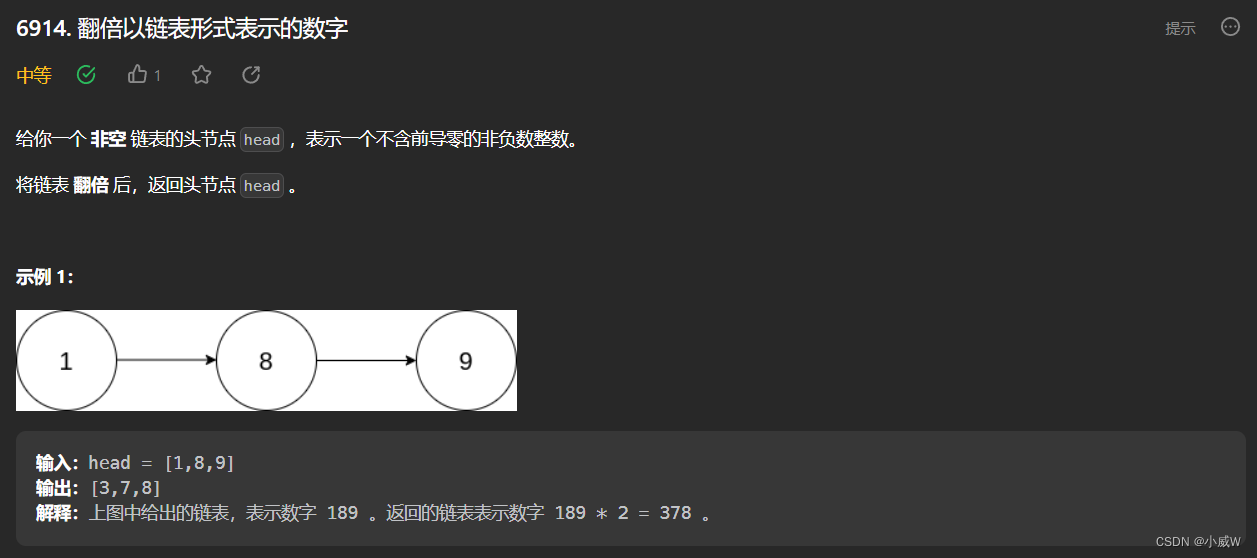
在这里插入图片描述
提示：
链表中节点的数目在范围 [1, 10^4] 内
0 <= Node.val <= 9
生成的输入满足：链表表示一个不含前导零的数字，除了数字 0 本身。

竞赛时代码——存入列表再计算

class Solution {public ListNode doubleIt(ListNode head) {// 存储列表List<Integer> ls = new ArrayList<>();while (head != null) {ls.add(head.val);head = head.next;}// 计算乘法int n = ls.size(), c = 0;for (int i = n - 1; i >= 0; --i) {int v = ls.get(i) * 2 + c;ls.set(i, v % 10);c = v / 10;}// 存入链表ListNode dummy = new ListNode(-1), prev = dummy;if (c == 1) ls.add(0, 1);for (int i = 0; i < n + c; ++i) {ListNode cur = new ListNode(ls.get(i));prev.next = cur;prev = cur;}return dummy.next;}
}

解法2——只有下一个节点大于 4 的时候，才会因为进位多加一

如果不考虑进位，就是每个节点的值乘以 2。
什么时候会受到进位的影响呢？只有下一个节点大于 4 的时候，才会因为进位多加一。
特别地，如果链表头的值大于 4，那么需要在前面插入一个新的节点。

class Solution {public ListNode doubleIt(ListNode head) {if (head.val > 4) head = new ListNode(0, head);for (ListNode cur = head; cur != null; cur = cur.next) {cur.val = cur.val * 2 % 10;if (cur.next != null && cur.next.val > 4) cur.val++;}return head;}
}

Q3：7022. 限制条件下元素之间的最小绝对差

https://leetcode.cn/problems/minimum-absolute-difference-between-elements-with-constraint/description/

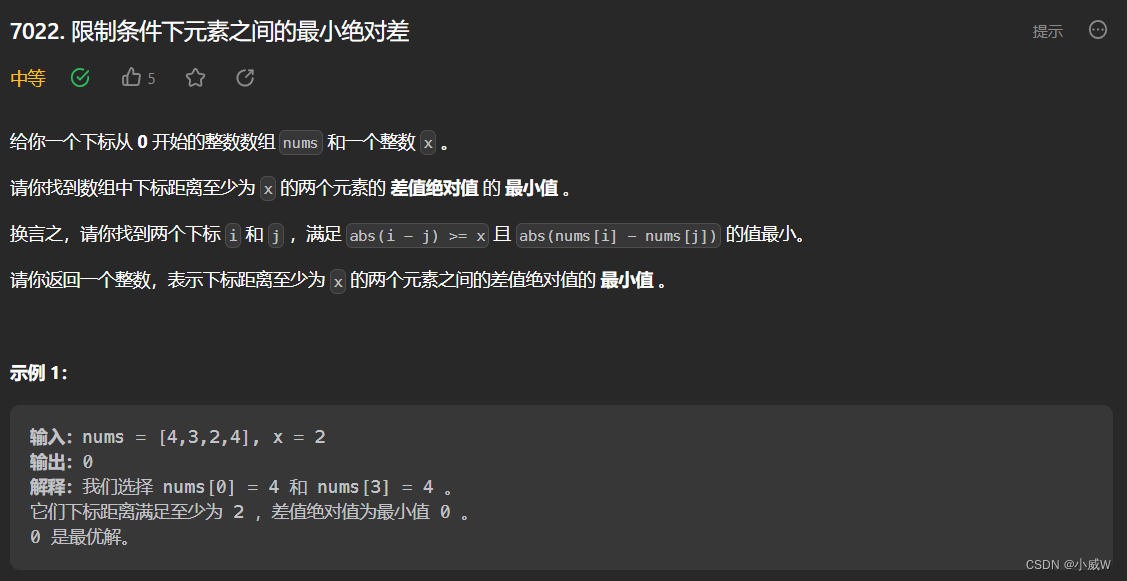
在这里插入图片描述
提示：
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
0 <= x < nums.length

竞赛时代码——手写二分

枚举 i 和 j ，其中 j = i + x，这样从 0 ~ i 范围内都是 nums[j] 可以配对的数字。
将 0 ~ i 的数字排序之后，就可以使用二分查找寻找其中最接近 nums[j] 的数字了。

class Solution {public int minAbsoluteDifference(List<Integer> nums, int x) {int n = nums.size(), ans = Integer.MAX_VALUE;List<Integer> ls = new ArrayList();         // 维护前面元素的有序序列（升序）for (int i = 0, j = x; j < n; ++i, ++j) {// 将nums[i]加入有序序列ls，使用二分查找寻找nums[i]应该插入的位置。int l = 0, r = ls.size(), v = nums.get(i);while (l < r) {int mid = l + r >> 1;if (ls.get(mid) <= v) l = mid + 1;else r = mid;}ls.add(l, v);// 使用二分查找寻找前面序列中最后一个<=nums[j]的元素l = 0;r = ls.size() - 1;v = nums.get(j);while (l < r) {int mid = l + r + 1 >> 1;if (ls.get(mid) > v) r = mid - 1;else l = mid;}// 使用和nums[j]最接近的元素更新答案ans = Math.min(ans, Math.abs(v - ls.get(l)));if (l + 1 < ls.size()) ans = Math.min(ans, Math.abs(ls.get(l + 1) - v));}return ans;}
}

写法2——使用API（TreeSet）

排序 和 二分查找的过程都可以使用 JDK 来实现。

class Solution {public int minAbsoluteDifference(List<Integer> nums, int x) {int n = nums.size(), ans = Integer.MAX_VALUE;TreeSet<Integer> s = new TreeSet<>();s.add(Integer.MAX_VALUE);s.add(Integer.MIN_VALUE / 2);for (int i = x; i < n; ++i) {s.add(nums.get(i - x));int y = nums.get(i);ans = Math.min(ans, Math.min(s.ceiling(y) - y, y - s.floor(y)));}return ans;}
}

TreeSet 会自动排序，关于 TreeSet 可见：https://docs.oracle.com/en/java/javase/11/docs/api/java.base/java/util/TreeSet.html#ceiling(E)

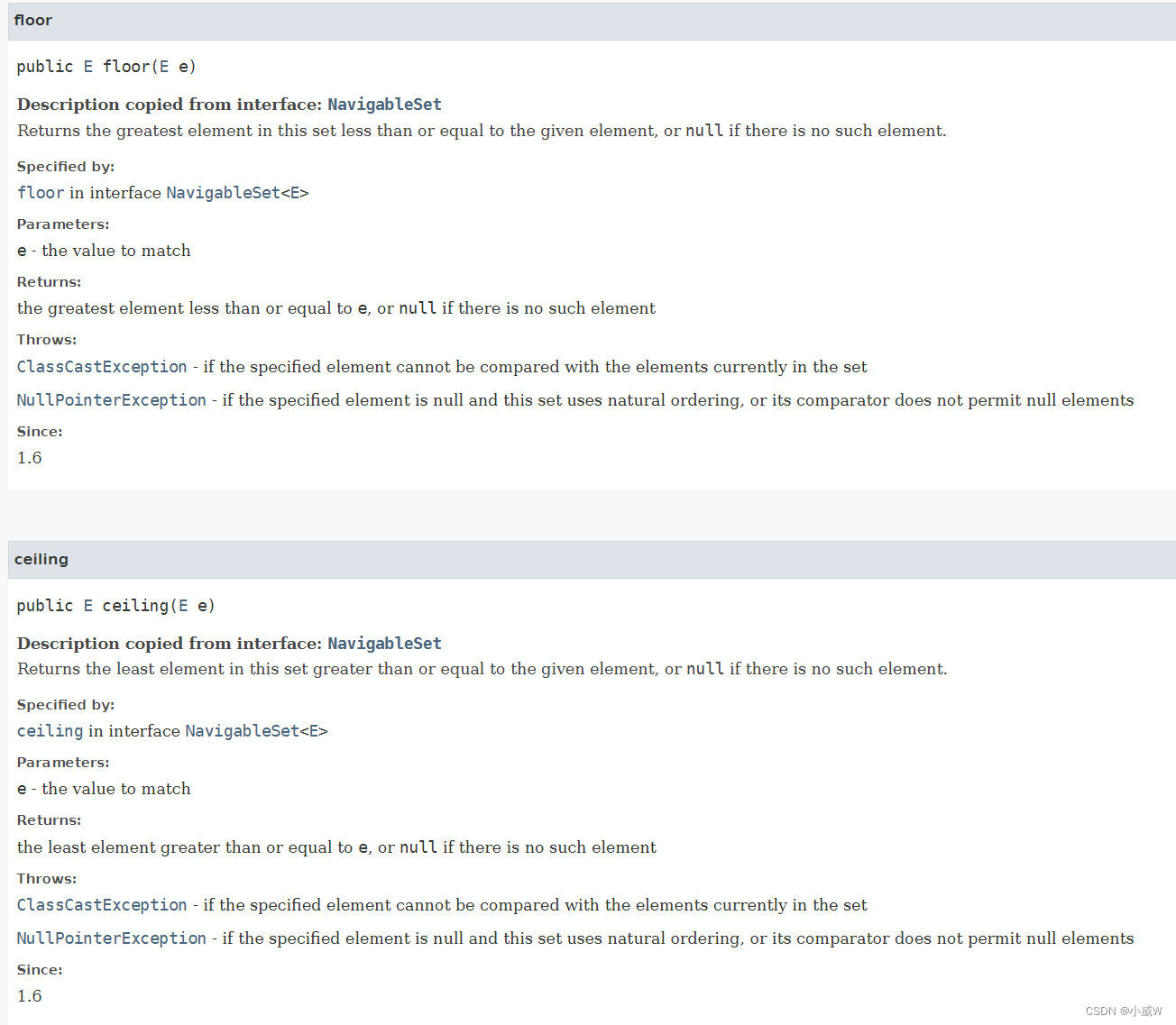
在这里插入图片描述

floor()：返回集合中小于或等于给定元素的最大元素，如果没有这样的元素，则返回null。
ceiling()：返回集合中大于或等于给定元素的最小元素，如果不存在这样的元素则返回null。

Q4：7023. 操作使得分最大（大杂烩：数学 + 单调栈(贡献法) + 贪心）

https://leetcode.cn/problems/apply-operations-to-maximize-score/

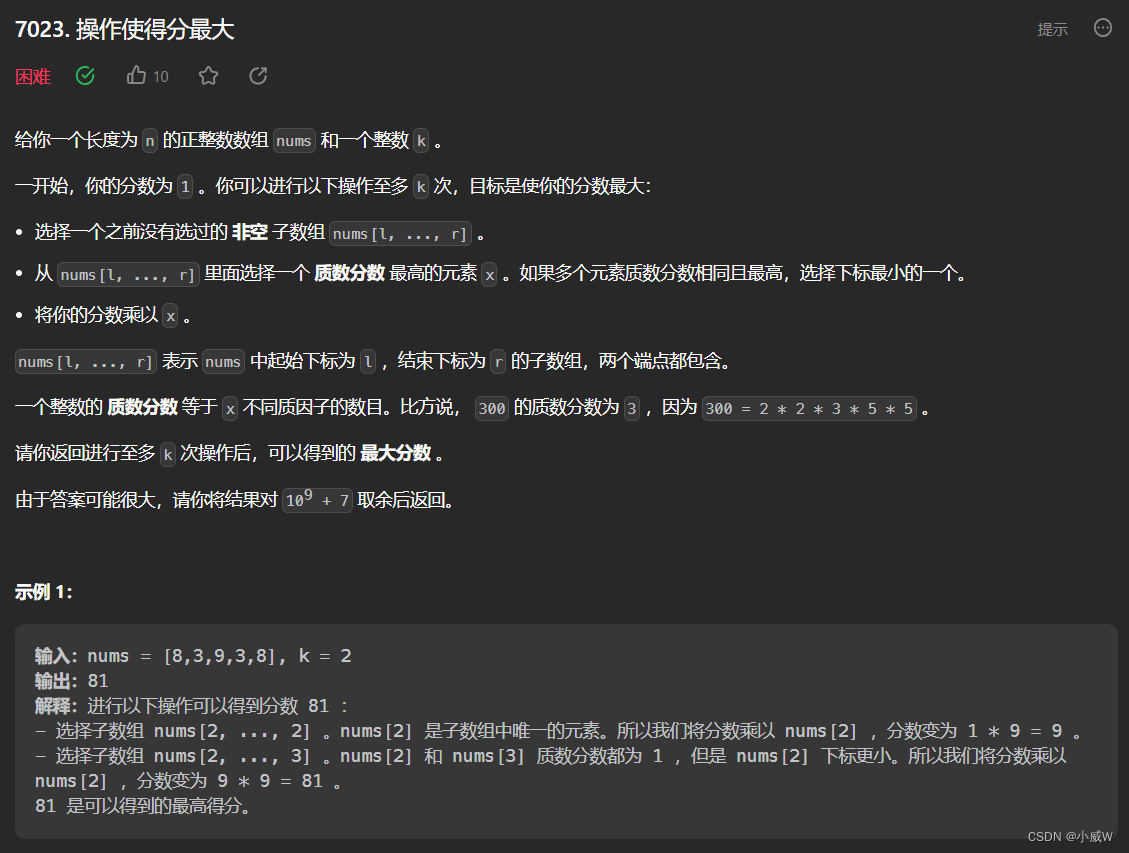
在这里插入图片描述

提示：
1 <= nums.length == n <= 10^5
1 <= nums[i] <= 10^5
1 <= k <= min(n * (n + 1) / 2, 10^9)

竞赛时代码

我们考虑每个数字 x 对应的 l ~ r 的范围，就是元素 x 可以被选择的次数。
一共可以选择 k 次，所以我们应该将元素按照贡献的能力排序，尽量选贡献大的，其中每个元素 x 可以被选择的次数通过单调栈求出 l ~ r 的范围即可。

质数分数的求法：质因数分解。
k 次操作之后的分数的求法：因为 k 可能很大，所以需要使用快速幂。

class Solution {final long MOD = (long)1e9 + 7;public int maximumScore(List<Integer> nums, int k) {int n = nums.size();int[][] scores = new int[n][2];for (int i = 0; i < n; ++i) {scores[i][0] = op(nums.get(i));         // 求质数分数}Deque<Integer> stk = new ArrayDeque<>();int[] l = new int[n], r = new int[n];       // 存储各个元素对应可以选择的l~r范围Arrays.fill(l, -1);Arrays.fill(r, n);for (int i = 0; i < n; ++i) {while (!stk.isEmpty() && scores[i][0] > scores[stk.peek()][0]) {r[stk.pop()] = i;}if (!stk.isEmpty()) l[i] = stk.peek();stk.push(i);}for (int i = 0; i < n; ++i) {scores[i][0] = nums.get(i);             // 元素的贡献scores[i][1] = (r[i] - i) * (i - l[i]); // 元素可以被选择的次数}// 排序+贪心找 k次操作对应哪些元素Arrays.sort(scores, (x, y) -> y[0] - x[0]);     // 分数倒序排序int sum = 0, id = 0, c = 0;for (int i = 0; i < n; ++i) {if (sum + scores[i][1] <= k) {sum += scores[i][1];id = i;c = scores[i][1];}else {id = i;c = k - sum;break;}}long ans = 1;ans = (ans * qmi((long)scores[id][0], (long)c)) % MOD;  // 把最后一个选c次的放进去for (int i = id - 1; i >= 0; --i) {ans = (ans * qmi((long)scores[i][0], (long)scores[i][1])) % MOD;}return (int)ans;}// 质因数分解 得到不同质因数的数量public int op(int x) {int res = 0;for (int i = 2; i <= x / i; ++i) {if (x % i == 0) {res++;while (x % i == 0) {x /= i;}}}if (x > 1) res++;return res;}// 快速幂public long qmi(long a, long b) {long p = MOD;long res = 1 % p, t = a;while (b != 0) {if ((b & 1) == 1) res = res * t % p;t = t * t % p;b >>= 1;}return res;}
}

相关子题目

质因数分解

求质因数分解

867. 分解质因数 https://www.acwing.com/problem/content/869/
见：https://blog.csdn.net/qq_43406895/article/details/131843296

import java.util.*;public class Main {public static void main(String[] args){Scanner sc = new Scanner(System.in);int n = sc.nextInt();while (n-- != 0) {divide(sc.nextInt());}}static void divide(int x) {for (int i = 2; i <= x / i; ++i) {if (x % i == 0) {int s = 0;while (x % i == 0) {        // 把 x 中的 i 除干净s++;x /= i;}System.out.println(i + " " + s);}}if (x > 1) System.out.println(x + " " + 1);     // 注意要判断最后剩下的没被除掉的质因数System.out.println();}
}

求质因数的数量

如果是只求质因数的数量的话，那么可以在筛质数的过程中记录质因数的数量。

对应解决这道题目的代码如下：

class Solution {final long MOD = (long)1e9 + 7;final static int MX = (int)1e5 + 1;// 求各个数字的不同质因数的数量static int[] omega = new int[MX];static {for (int i = 2; i < MX; ++i) {if (omega[i] == 0) {    // i 是质数for (int j = i; j < MX; j += i) {omega[j]++;     // i 是 j 的一个质因子}}}}public int maximumScore(List<Integer> nums, int k) {int n = nums.size();int[][] scores = new int[n][2];for (int i = 0; i < n; ++i) {scores[i][0] = op(nums.get(i));         // 求质数分数}Deque<Integer> stk = new ArrayDeque<>();int[] l = new int[n], r = new int[n];       // 存储各个元素对应可以选择的l~r范围Arrays.fill(l, -1);Arrays.fill(r, n);for (int i = 0; i < n; ++i) {while (!stk.isEmpty() && scores[i][0] > scores[stk.peek()][0]) {r[stk.pop()] = i;}if (!stk.isEmpty()) l[i] = stk.peek();stk.push(i);}for (int i = 0; i < n; ++i) {scores[i][0] = nums.get(i);             // 元素的贡献scores[i][1] = (r[i] - i) * (i - l[i]); // 元素可以被选择的次数}// 排序+贪心找 k次操作对应哪些元素Arrays.sort(scores, (x, y) -> y[0] - x[0]);     // 分数倒序排序int sum = 0, id = 0, c = 0;for (int i = 0; i < n; ++i) {if (sum + scores[i][1] <= k) {sum += scores[i][1];id = i;c = scores[i][1];}else {id = i;c = k - sum;break;}}long ans = 1;ans = (ans * qmi((long)scores[id][0], (long)c)) % MOD;  // 把最后一个选c次的放进去for (int i = id - 1; i >= 0; --i) {ans = (ans * qmi((long)scores[i][0], (long)scores[i][1])) % MOD;}return (int)ans;}// 质因数分解 得到不同质因数的数量public int op(int x) {return omega[x];}// 快速幂public long qmi(long a, long b) {long p = MOD;long res = 1 % p, t = a;while (b != 0) {if ((b & 1) == 1) res = res * t % p;t = t * t % p;b >>= 1;}return res;}
}

快速幂

力扣题目链接：https://leetcode.cn/problems/powx-n/
在这里插入图片描述

参见：【算法基础：数学知识】4.4 快速幂

递归版——

    static long qmi(long a, long b, long p) {if (b == 0) return 1;long res = qmi(a, b / 2, p) % p;if (b % 2 == 0) return res * res % p;else return res * res * a % p;}

迭代版——

    static long qmi(long a, long b, long p) {long res = 1 % p, t = a;// 把 b 看成二进制数字，哪些位置是 1 就把它乘起来就好了while (b != 0) {if ((b & 1) == 1) res = res * t % p;t = t * t % p;b >>= 1;}return res;}

成绩记录

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/90614.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

R语言生存分析算法的简单组合

R语言生存分析算法的简单组合

library(survival) library(randomForestSRC)# 生成模拟数据 set.seed(123) n <- 200 time <- rexp(n, rate 0.1) status <- rbinom(n, size 1, prob 0.7) var1 <- rnorm(n) var2 <- rnorm(n) var3 <- rnorm(n) data1 <- data.frame(time time, statu…
阅读更多...
PLL 的 verilog 实现

PLL 的 verilog 实现

锁相环&#xff08;PLL&#xff09;是一种常用的频率、相位追踪算法&#xff0c;在信号解调、交流并网等领域有着广泛的应用。本文对全数字锁相环的原理进行介绍&#xff0c;随后给出 verilog 实现及仿真。 PLL 锁相原理 锁相环结构如下图所示&#xff0c;主要由鉴相器、环路滤…
阅读更多...
UDP通信实验、广播与组播、本地套接字

UDP通信实验、广播与组播、本地套接字

文章目录 流程函数应用广播应用 组播&#xff08;多播&#xff09;本地套接字应用 流程 函数 返回值&#xff1a; 成功&#xff0c;返回成功发送的数据长度 失败&#xff0c;-1 返回值&#xff1a; 成功&#xff0c;返回成功接收数据长度 失败&#xff0c;-1 应用 广播 应用 …
阅读更多...
【不限于联想Y9000P电脑关盖再打开时黑屏的解决办法】

【不限于联想Y9000P电脑关盖再打开时黑屏的解决办法】

不限于联想Y9000P电脑关盖再打开时黑屏的解决办法 问题的前言问题的出现问题拟解决 问题的前言 事情发生在昨天&#xff0c;更新了Win11系统后&#xff1a; 最惹人注目的三处地方就是&#xff1a; 1.可以查看时间的秒数了&#xff1b; 2.右键展示的内容变窄了&#xff1b; 3.按…
阅读更多...
湖南科技学院图书馆藏八一新书《乡村振兴战略下传统村落文化旅游设计》

湖南科技学院图书馆藏八一新书《乡村振兴战略下传统村落文化旅游设计》

湖南科技学院图书馆藏八一新书《乡村振兴战略下传统村落文化旅游设计》
阅读更多...
20230815在淘宝的代扫描服务【仅供参考】

20230815在淘宝的代扫描服务【仅供参考】

20230815在淘宝的代扫描服务【仅供参考】 2023/8/15 12:35 https://item.taobao.com/item.htm?spma21n57.1.0.0.3d47523caCFZ3T&id601206116790&ns1&abbucket4#detail e邦生活服务 https://item.taobao.com/item.htm?_ufju3ku42b4&id629900806906 寄书扫描…
阅读更多...
奥威BI数据可视化工具：报表就是平台，随时自助分析

奥威BI数据可视化工具：报表就是平台，随时自助分析

别的数据可视化工具&#xff0c;报表就只是报表&#xff0c;而奥威BI数据可视化工具&#xff0c;一张报表就约等于一个平台&#xff0c;可随时展开多维动态自助分析&#xff0c;按需分析&#xff0c;立得数据信息。 奥威BI是一款多维立体分析数据的数据可视化工具。它可以帮助…
阅读更多...
JavaFx基础学习【五】：FXML布局文件使用

JavaFx基础学习【五】：FXML布局文件使用

目录 前言 一、介绍 二、简单体验 三、FXML标签元素 四、fx属性介绍 五、重写initialize&#xff08;名字需要保持一致&#xff09;方法 六、Scene Builder快速布局 前言 如果你还没有看过前面的文章&#xff0c;可以通过以下链接快速前往学习&#xff1a; JavaFx基础学…
阅读更多...
Vscode 常用操作教程

Vscode 常用操作教程

一、语言换成中文 这是我们可以直接点击左边栏第四个图标搜索插件 chinese ,也可以直接ctrlshiftp快捷键也会出来如图所示图标&#xff0c;出来chinese 插件之后选择安装install,安装完成之后重新ctrlshiftp会出现如图所示页面 找到我的鼠标在的地方对应的中文&#xff0c;此时…
阅读更多...
2023国赛 高教社杯数学建模ABCDE题思路汇总分析

2023国赛 高教社杯数学建模ABCDE题思路汇总分析

文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料 0 赛题思路 &#xff08;赛题出来以后第一时间在CSDN分享&#xff09; https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 全国大学生数学建模…
阅读更多...
R语言实现随机生存森林（2）

R语言实现随机生存森林（2）

library(survival) library(randomForestSRC) help(package"randomForestSRC") #构建普通的随机生存森林 data(cancer,package"survival") lung$status<-lung$status-1 rfsrc.fit1 <- rfsrc(Surv(time, status) ~ ., lung,ntree 100,block.size 1,…
阅读更多...
react入门到实战 学习笔记1 搭建

react入门到实战 学习笔记1 搭建

一、React是什么 一个专注于构建用户界面的 JavaScript 库&#xff0c;和vue和angular并称前端三大框架 React有什么特点 1- 声明式UI&#xff08;JSX&#xff09; 写UI就和写普通的HTML一样&#xff0c;抛弃命令式的繁琐实现 2- 组件化 组件是react中最重要的内容&#xf…
阅读更多...
开学季值得买电容笔有哪些？推荐平价好用的电容笔

开学季值得买电容笔有哪些？推荐平价好用的电容笔

大多数的学生党都没有稳定的经济来源&#xff0c;因此在挑选东西时都追求着高性价比。随着iPad平板电脑的性能不断提高&#xff0c;其所具备的功能将不断增加&#xff0c;它将逐渐融入我们的生活与工作。由于电子产品的不断升级&#xff0c;软件的改进&#xff0c;使得电容笔的…
阅读更多...
DNS部署与安全详解（下）

DNS部署与安全详解（下）

文章目录 前言一、指定区域解析配置二、DNS服务器对外名称显示配置三、转发器使用配置四、配置辅助&#xff08;备份&#xff09;服务器五、如何让虚拟机可以真实上网六、为DNS服务器配置别名 前言 上一篇博客我们已经在Windows server2003的虚拟机上下载了DNS软件&#xff0c;…
阅读更多...
企业中商业智能BI，常见的工具和技术

企业中商业智能BI，常见的工具和技术

商业智能&#xff08;Business Intelligence&#xff0c;简称BI&#xff09;数据可视化是通过使用图表、图形和其他可视化工具来呈现和解释商业数据的过程。它旨在帮助组织更好地理解和分析他们的数据&#xff0c;从而做出更明智的商业决策。 常见的商业智能数据可视化工具和技…
阅读更多...
安卓：LitePal操作数据库

安卓：LitePal操作数据库

目录 一、LitePal介绍 常用方法&#xff1a; 1、插入数据&#xff1a; 2、更新数据&#xff1a; 3、删除数据&#xff1a; 4、查询数据&#xff1a; 二、LitePal的基本用法&#xff1a; 1、集成LitePal&#xff1a; 2、创建LitePal配置文件&#xff1a; 3、创建模型类…
阅读更多...
内网ip与外网ip

内网ip与外网ip

一、关于IP地址 我们平时直接接触最多的是内网IP。而且还可以自己手动修改ip地址。而外网ip&#xff0c;我们很少直接接触&#xff0c;都是间接接触、因为外网ip一般都是运营商管理&#xff0c;而且是全球唯一的&#xff0c;一般我们自己是无法修改的。 内网IP和外网IP是指在…
阅读更多...
SQL | 使用通配符进行过滤

SQL | 使用通配符进行过滤

6-使用通配符进行过滤 6.1-LIKE操作符 前面介绍的所有操作符都是通过已知的值进行过滤&#xff0c;或者检查某个范围的值。但是如果我们想要查找产品名字中含有bag的数据&#xff0c;就不能使用前面那种过滤情况。 利用通配符&#xff0c;可以创建比较特定数据的搜索模式。 …
阅读更多...
Open3D 最小二乘拟合平面（SVD分解法）

Open3D 最小二乘拟合平面（SVD分解法）

目录 一、算法原理二、代码实现三、结果展示1、点云2、拟合结果四、优秀博客本文由CSDN点云侠原创，原文链接。爬虫网站自重。 一、算法原理 本文实现矩阵奇异值分解方法的最小二乘拟合平面。原理如下： 对于得到的 n n
阅读更多...
8 张图 | 剖析 Eureka 的首次同步注册表

8 张图 | 剖析 Eureka 的首次同步注册表

注册表对于注册中心尤为重要&#xff0c;所有的功能都是围绕这个注册表展开。比如服务 A 要想访问服务 B&#xff0c;就得知道服务 B 的 IP 地址和端口号吧。如下图所示&#xff0c;传统的方式就是服务 A 知道了服务 B 的地址后&#xff0c;发送 HTTP 请求到对应的 API 地址上。…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023