👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习—语言模型和数据集
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
循环神经网络RNN
- 引入
- 无隐状态的神经网络
- 有隐状态的循环神经网络
- 具有循环神经网络的字符级语言模型
- 困惑度
- 小结
引入
在之前介绍了n元语法模型,其中单词xt在时间步t的概率仅取决于前n-1个单词。对于时间步t-(n-1)之前的打你,若我们想将其可能产生的影响合并到xt上,需要增加n,模型参数的数量也会指数增长,因为词表V需要存储|V|n个数字,因此我们不如使用隐变量:
P ( x t ∣ x t − 1 , . . . , x 1 ) ≈ P ( x t ∣ h t − 1 ) P(x_t|x_{t-1},...,x_1)≈P(x_t|h_{t-1}) P(xt∣xt−1,...,x1)≈P(xt∣ht−1)
其中h表示隐藏变量,存储到时间步t-1的序列信息。
h t = f ( x t , h t − 1 ) h_t=f(x_t,h_{t-1}) ht=f(xt,ht−1)
值得注意的是,隐藏层和隐状态指的是两个截然不同的概念。如上所述,隐藏层是在从输入到输出的路径上(以观测角度来理解)的隐藏的层,而隐状态则是在给定步骤所做的任何事情(以技术角度来定义)的输入,并且这些状态只能通过先前时间步的数据来计算。
RNN是具有隐状态的神经网络
无隐状态的神经网络
对于只有单隐藏层的多层感知机,其隐藏层输出为:
H = φ ( X W x h + b h ) H=φ(XW_{xh}+b_h) H=φ(XWxh+bh)
将隐藏变量H用作输出层的输入,则其输出层为:
O = H W h q + b q O=HW_{hq}+b_q O=HWhq+bq
有隐状态的循环神经网络
有了隐状态后,情况就完全不同了。与多层感知机不同的是, 我们在这里保存了前一个时间步的隐藏变量:
H t − 1 H_{t-1} Ht−1
并引入了一个新的权重参数:
W h h W_{hh} Whh
用来描述如何在当前时间步中使用前一个时间步的隐藏变量。
而当前时间步隐藏变量由当前时间步的输入与前一个时间步的隐藏变量一起计算得出:
H t = φ ( X t W x h + H t − 1 W h h + b h ) H_t=φ(X_tW_{xh}+H_{t-1}W_{hh}+b_h) Ht=φ(XtWxh+Ht−1Whh+bh)
这些变量捕获并保留了序列直到其当前时间步的历史信息,就如当前时间步下神经网络的状态或记忆,因此这样的隐藏变量被称为隐状态。
由于隐状态使用的定义与前一个时间步中使用的定义相同,因此上式是循环的,基于上式的网络就称为循环神经网络RNN,执行上式的层就叫做循环层。
对于时间步t,输出层的输出类似于多层感知机:
O t = H t W h q + b q O_t=H_tW_{hq}+b_q Ot=HtWhq+bq
值得一提的是,即使在不同的时间步,循环神经网络也总是使用这些模型参数。因此,循环神经网络的参数开销不会随着时间步的增加而增加。
下面展示了RNN计算逻辑:
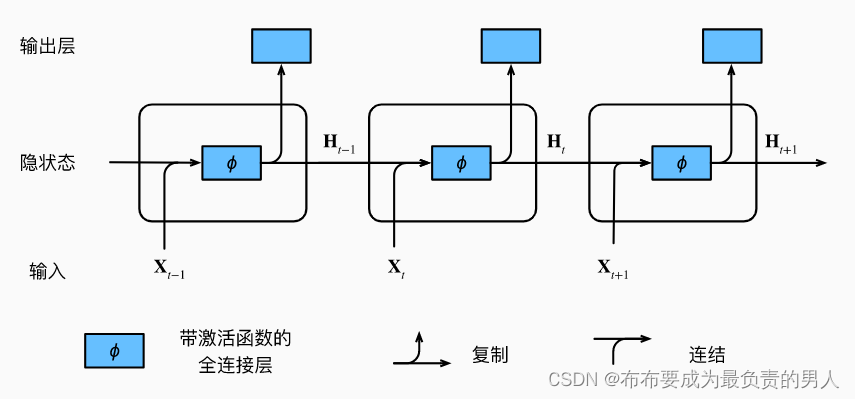
在任意时间步,隐状态的计算可以被视为:
1、拼接当前时间步t的输入和前一时间步t-1的隐状态
2、将拼接结果送入带有激活函数的全连接层,全连接层的输出是当前时间步t的隐状态
具有循环神经网络的字符级语言模型
设小批量大小为1,批量中的文本序列为“machine”。使用字符级语言模型,将文本次元化为字符而不是单词,如下图演示,使用当前的和先前的字符预测下一个字符:
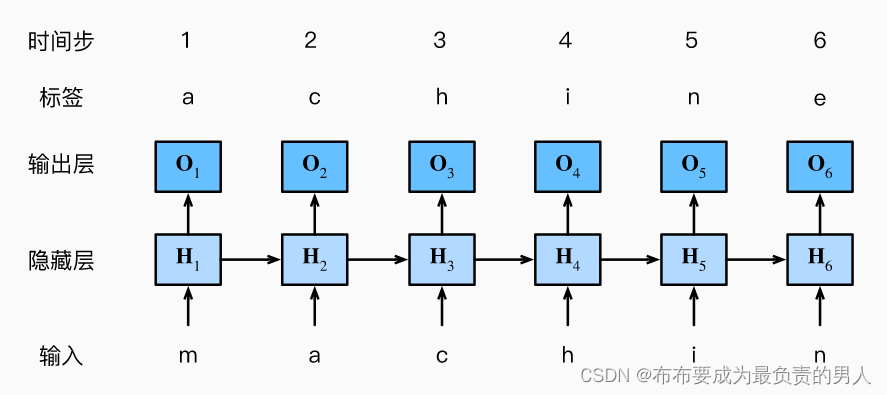
在训练过程中,我们对每个时间步的输出层的输出进行softmax操作, 然后利用交叉熵损失计算模型输出和标签之间的误差。
在实践中,我们使用的批量大小是n>1,每个词元都由一个d维向量表示,因此,我们在时间步t的输入是一个n×d的矩阵。
困惑度
让我们讨论如何度量语言模型的质量,这将在后续部分中用于评估基于循环神经网络的模型。
我们可以通过一个序列中所有的n个词元的交叉熵损失的平均值来衡量:
1 n ∑ t = 1 n − l o g P ( x t ∣ x t − 1 , . . . , x 1 ) \frac{1}{n}\sum_{t=1}^n-logP(x_t|x_{t-1},...,x_1) n1t=1∑n−logP(xt∣xt−1,...,x1)
其中,P由语言模型给出,xt是在时间步t从该序列中观察到的实际词元。
而我们使用的是困惑度,是一个指数:
e x p ( − 1 n ∑ t = 1 n l o g P ( x t ∣ x t − 1 , . . . , x 1 ) ) exp(-\frac{1}{n}\sum_{t=1}^nlogP(x_t|x_{t-1},...,x_1)) exp(−n1t=1∑nlogP(xt∣xt−1,...,x1))
困惑度的最好的理解是“下一个词元的实际选择数的调和平均数”。
在接下来,我们将基于循环神经网络实现字符级语言模型,并使用困惑度来评估这样的模型。
小结
1、对隐状态使用循环计算的神经网络称为循环神经网络(RNN)
2、循环神经网络的隐状态可以捕获直到当前时间步序列的历史信息
3、循环神经网络模型的参数数量不会随着时间步的增加而增加
4、我们可以使用循环神经网络创建字符级语言模型
5、我们可以使用困惑度来评价语言模型的质量