梯度

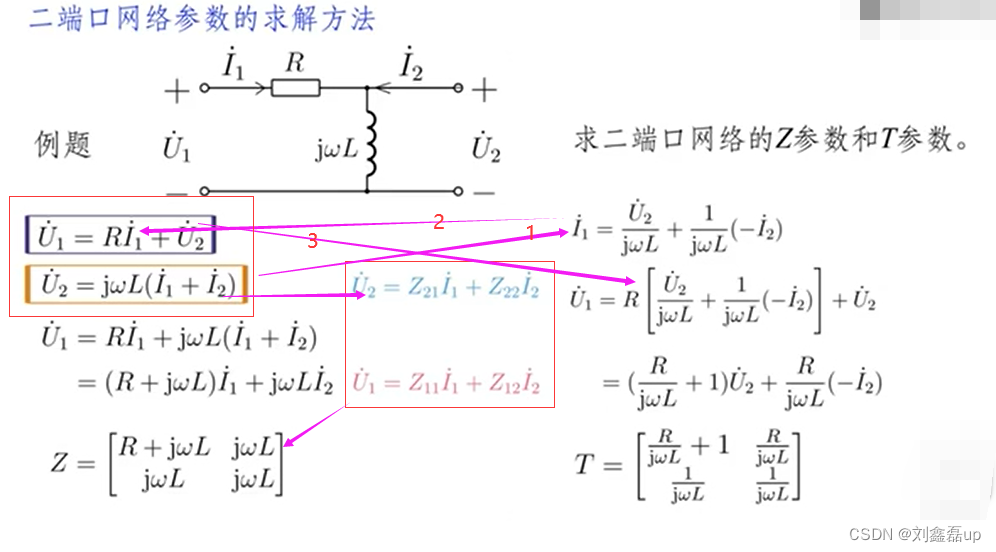
在高数中，梯度是一个向量，是有方向有大小。假设一二元函数f(x,y)，在某点的梯度有：

结果为：

即方向导数。梯度的方向是函数变化最快的方向，沿着梯度的方向容易找到最大值。

图像梯度

在一幅模糊图像中的物体的轮廓不明显，轮廓边缘灰度变化不强烈，从而导致层次感不强，而在清晰图片中的物体轮廓边缘灰度变化明显，层次感强。那么这种灰度变化明显不明显怎么去定义呢？

可以使用导数（梯度），衡量图像灰度的变化率，因为图像就是函数。正因如此，我们引入的图像梯度可以把图像看成二维离散函数，图像梯度其实就是这个二维离散函数的求导。

如果一副图像的相邻灰度值有变化，那么梯度就存在，如果图像相邻的像素没有变化，那么梯度就是0，把梯度值和相应的像素相加，那么灰度值没有变化的，像素就没有变化，灰度值变了，像素值也就变了。
相加后的新图像，原图像像素点100与90亮度只相差10，现在是110与90，亮度相差20了，对比度显然增强了，尤其是图像中物体的轮廓和边缘，与背景大大加强了区别，这就是用梯度来增强图像的原理。将图像函数f(x,y)梯度表达式表示出来：

幅度：

方向角：

对于数字图像来说，相当于是二维离散函数求梯度，使用差分来近似导数：

因此，像素点(x,y)处的梯度值和梯度方向分别是：

平方+开方的，计算量太大，于是一般用绝对值来近似平方和平方根的操作，来降低计算量：

梯度的方向是函数变化最快的方向，所以当函数中存在边缘时，一定有较大的梯度值，相反，当图像中有比较平滑的部分时，灰度值变化较小，则相应的梯度也较小，图像处理中把梯度的模简称为梯度，由图像梯度构成的图像成为梯度图像。

一些经典的图像梯度算法是考虑图像的每个像素的某个邻域内的灰度变化，利用边缘临近的一阶或二阶导数变化规律，对原始图像中像素某个邻域设置梯度算子，通常我们用小区域模板进行卷积来计算，有Sobel算子、Robinson算子、Laplace算子等。

经典算子

对图像大矩阵和滤波小矩阵对应位置元素相乘再求和的操作就叫卷积(Convolution)或协相关(Correlation).

协相关(Correlation)和卷积(Convolution)很类似，两者唯一的差别就是卷积在计算前需要翻转卷积核，而协相关则不需要翻转.

sobel算子

主要用作边缘检测，是离散差分算子，用来运算图像梯度函数的灰度近似值。在图像的任何一点使用此算子，将会产生对应的梯度矢量或者法矢量。

书上的sobel模板不是卷积模板，而是协相关模板，卷积的话要先将模板旋转180度以后再与图像做相关操作。

Gx方向的相关模板：

Gy方向的相关模板：

Sobel的卷积模板Gx：

sobel卷积模板Gy：

具体计算为，每个像素（灰度值）与模板对应位置元素相乘求和（类似于CNN中的卷积，其实是协相关运算），来计算该点灰度的大小：

为了提高效率使用不开平方的近似值：

用以下公式计算梯度方向：

Sobel算子用来计算图像灰度函数的近似梯度。Sobel算子根据像素点上下、左右邻点灰度加权差，在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用，提供较为精确的边缘方向信息，边缘定位精度不够高。当对精度要求不是很高时，是一种较为常用的边缘检测方法。

部分算子介绍