分数 15

全屏浏览题目

切换布局

作者 C课程组

单位 浙江大学

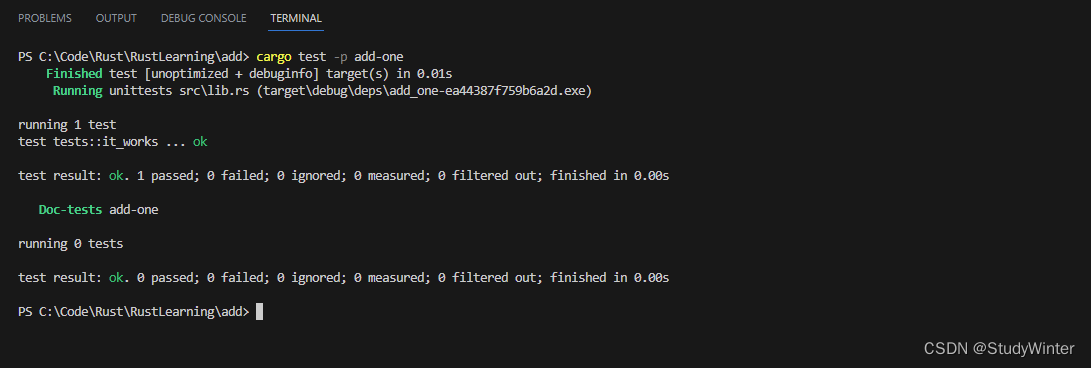
本题要求编写程序，计算序列部分和 1 - 1/4 + 1/7 - 1/10 + ... 直到最后一项的绝对值不大于给定精度eps。

输入格式:

输入在一行中给出一个正实数eps。

输出格式:

在一行中按照“sum = S”的格式输出部分和的值S，精确到小数点后六位。题目保证计算结果不超过双精度范围。

输入样例1:

4E-2

输出样例1:

sum = 0.854457

输入样例2:

0.02

输出样例2:

sum = 0.826310

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

我的答案：

C语言：

#include <stdio.h>int main() {double eps, sum = 0.0, term;int i = 1, sign = 1;  // 初始化i和符号signscanf("%lf", &eps);while(1) {term = 1.0 / (3 * i - 2);  // 计算当前项if(term <= eps) break;  // 检查终止条件sum += sign * term;  // 根据符号累加到sumsign = -sign;  // 符号取反，实现交替效果i++;  // 移动到下一个项}printf("sum = %.6f\n", sum);return 0;
}

 C++：
 

#include <iostream>
#include <iomanip>using namespace std;int main() {double eps, sum = 0.0, term;int i = 1, sign = 1;  // 初始化i和符号signcin >> eps;while(1) {term = 1.0 / (3 * i - 2);  // 计算当前项if(term <= eps) break;  // 检查终止条件sum += sign * term;  // 根据符号累加到sumsign = -sign;  // 符号取反，实现交替效果i++;  // 移动到下一个项}cout << "sum = " << fixed << setprecision(6) << sum << endl;return 0;
}

解题过程分析:

1. 初始化部分: 首先，我们定义了eps存储精度，sum存储序列的部分和，term存储当前项的值。为了确保正负号的交替，我们定义了一个名为sign的变量，初始值为1。每次使用完后都取反。

2. 计算部分和: 使用while循环继续添加项，直到当前项的绝对值小于或等于eps为止。每次迭代，我们都会计算新的项，并更新sum。每次迭代后，我们还要更新i的值和sign的值。

3. 输出: 使用固定的浮点数格式和六位精度输出结果。

这种方式的解题方法侧重于观察数学序列的规律，并将其转化为算法实现。

总结：

从这道题目，我们可以学到以下几点：

1. **观察数学规律**: 解决这类题目的关键是首先找到数学序列的规律。在本题中，我们观察到序列的分子始终为1，分母是递增的，每次增加3，且正负号是交替的。

2. **循环控制**: 了解如何使用循环来累加序列，并掌握如何根据某个条件（在这里是项的绝对值小于或等于`eps`）来终止循环。

3. **处理浮点数精度**: 在处理涉及浮点数的题目时，特别是当需要特定精度的输出时，我们应该知道如何设置输出的精度（例如，在C++中使用`setprecision`）。

4. **交替符号技巧**: 通过使用一个整数`sign`，其值在1和-1之间切换，我们可以轻松地实现一个交替系列。这是处理交错系列或任何需要切换两种状态的问题的一个常见技巧。

5. **简洁的代码结构**: 从这题的解法中，我们可以看到如何组织代码结构使其既简洁又易于理解。例如，我们使用一个简单的`while`循环来计算部分和，而不是复杂的多重循环或条件结构。

6. **问题建模**: 学会如何将实际问题或数学问题建模为计算问题，然后用算法来解决。这是计算思维的核心。

总的来说，这道题目是一个很好的入门级题目，它结合了基本的编程技巧和数学知识，帮助我们提高了解决实际问题的能力。