什么是生产消费者模型

生产者消费者模型是一种常见的并发编程模型，用于解决生产者和消费者之间数据交换和同步的问题。在这个模型中，生产者会生成数据并将其放入共享的缓冲区或队列中，而消费者则从缓冲区中取出数据进行处理。

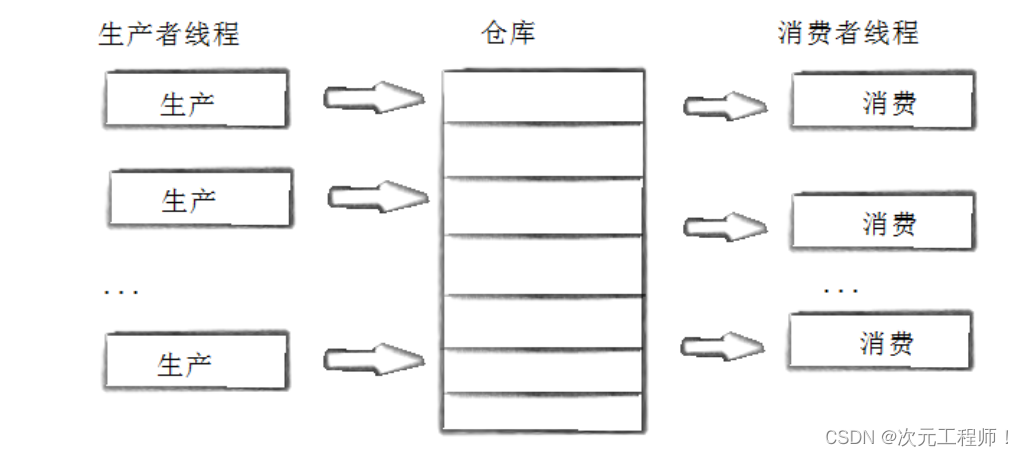
该模型图如下：

321原则：

上面的图中，我们可以把生产者看成是超市的供应商，仓库就是所谓的超市，而消费者就是顾客。

它们之间存在3种关系：

生产者和生产者：竞争，即互斥关系。比如供应商间会竞争在超市中上架自己的产品。

消费者和消费者：竞争，即互斥关系。 因为超市有很多货物，所以这种现象不明显，但是假设商家提供某个物品的促销活动，这个时候消费者便会抢，竞争性也就很明显了。

生产者和消费者：互斥/同步关系。要么生产者在超市放入，要么消费者在消费，两者必须互斥，不能一起，而且一定有顺序。

2种角色: 生产者/消费者.

1个交易场所：超市

后面的代码将按照这个321原则进行编写.

为什么要使用生产消费者模型

解耦和提高系统灵活度：生产者消费者模式就是通过一个容器来解决生产者和消费者的强耦合问题。生产者和消费者彼此之间不直接通讯，而通过阻塞队列来进行通讯，所以生产者生产完数据之后不用等待消费者处理，直接扔给阻塞队列，消费者不找生产者要数据，而是直接从阻塞队列里取，阻塞队列就相当于一个缓冲区，平衡了生产者和消费者的处理能力。这个阻塞队列就是用来给生产者和消费者解耦的。

并行处理和提高系统效率：生产者消费者模型能够并行处理数据，允许生产者和消费者以独立的方式执行。生产者可以持续地生成数据，而消费者则以自己的速度进行处理。这样可以提高系统的处理能力和效率，充分利用多核处理器和并发编程的潜力。

基于阻塞队列的生产消费者模型

在多线程编程中阻塞队列(Blocking Queue)是一种常用于实现生产者和消费者模型的数据结构。其与普通的队列区别在于，当队列为空时，从队列获取元素的操作将会被阻塞，直到队列中被放入了元素；当队列满时，往队列里存放元素的操作也会被阻塞，直到有元素被从队列中取出(以上的操作都是基于不同的线程来说的，线程在对阻塞队列进程操作时会被阻塞)。

这里再来说一个结论：

进程间通信的前提是：让不同进程看到同一份资源。

进程间通信的本质是：生产消费者模型（一方写入数据，一方接受数据）

所以我们之前提到的管道，内部也是一个简单的阻塞队列，有数据就接收，没数据就阻塞等待。

所以接下来我们要自己实现一个基于阻塞队列的生产消费者模型

整体思路是：先设计一个BlockQueue类表示阻塞队列，然后里面一共包含五个成员变量：分别为

queue类型bq_代表队列，capacity_代表队列的容量，mtx_代表互斥锁，两个条件变量：Empty_代表当前阻塞队列是否为空,Full_代表阻塞队列是否已满。

然后提供四个接口：

push()：生产者生产数据需要将其push到阻塞队列中，首先要检测临界资源是否满足条件，满足条件后再访问临界资源，否则pthread_cond_wait将该线程等待挂起。当访问完成后，给另一个条件变量Empty_利用pthread_cond_signal发送信号。
pop()：消费者每次消费数据需要将阻塞队列中的数据pop()，然后依然要检测临界资源是否满足条件,不满足pthread_cond_wait将线程等待挂起，满足条件后访问临界资源。然后给另一个条件变量Full_发送信号。
isQueueEmpty()&&isQueueFull()：判断阻塞队列是否为空，或者阻塞队列是否已满

类设计完成后，在主函数中，创建两个线程，分别代表生产者和消费者，然后各自执行对应的回调函数，生产者不断push，而消费者每隔一秒pop一次。

这样我们观察到的现象应该是：生产者很快将阻塞队列填满，然后便挂起等待，消费者每隔一秒取一次数据，然后给Full_发送信号唤醒生产者，然后生产者继续生产，此时满了之后又挂起等待，消费者隔一秒消费一次数据后，又将生产者唤醒...

所以整体的代码如下：

BlockQueue.hpp文件

#pragma once#include <iostream>
#include <queue>
#include <mutex>
#include <pthread.h>
using namespace std;
#define DEFAULT_CAP 5template <class T>
class BlockQueue
{
public:BlockQueue(int capacity = DEFAULT_CAP) : capacity_(capacity){pthread_mutex_init(&mtx_, nullptr);pthread_cond_init(&Empty_, nullptr);pthread_cond_init(&Full_, nullptr);}void push(const T &in) // 生产者{pthread_mutex_lock(&mtx_);// 1.先检测临界资源是否能够满足访问条件// break;//不要break，不然下次线程还可能继续进来，死循环// pthread_cond_wait:我们此时在临界区中，是持有锁的，如果去挂起等待了，那锁怎么办呢.// 消费者由于无法申请锁，也没办法拿出资源,所以它的第二个参数是一个锁，成功调用wait后，传入的锁会被自动释放// 当被唤醒时，线程会从哪里醒来呢：从哪里挂起，就从哪里唤醒// 当线程被唤醒的时候，pthread_cond_wait会自动帮线程获取锁。// pthread_cond_wait:只要是一个函数，就有可能能调用失败，所以调用失败时，会存在伪唤醒的情况，所以要把if换成whilewhile (isQueueFull()){pthread_cond_wait(&Full_, &mtx_);}// 2.访问临界资源bq_.push(in);//if (bq_.size() >= capacity_ / 2) //制定策略，可以自己随便设置pthread_cond_signal(&Empty_);pthread_mutex_unlock(&mtx_);}void pop(T *out){pthread_mutex_lock(&mtx_);while (isQueueEmpty())pthread_cond_wait(&Empty_, &mtx_);*out = bq_.front();bq_.pop();pthread_cond_signal(&Full_);pthread_mutex_unlock(&mtx_);}bool isQueueEmpty(){return bq_.size() == 0;}bool isQueueFull(){return bq_.size() == capacity_;}~BlockQueue(){pthread_mutex_destroy(&mtx_);pthread_cond_destroy(&Empty_);pthread_cond_destroy(&Full_);}private:queue<T> bq_;          // 阻塞队列int capacity_;         // 容量上线pthread_mutex_t mtx_;  // 通过互斥锁保证队列安全pthread_cond_t Empty_; // 表示把bq是否为空pthread_cond_t Full_;  // 表示bq是否满
};

ConProd.cc文件

#include "BlockQueue.hpp"
#include<unistd.h>void* consumer(void* args)
{BlockQueue<int>* bqueue = (BlockQueue<int>*)args;while(true){int a = 0;bqueue->pop(&a);cout << "消费了一个数据： " << a << endl;sleep(1);}return nullptr;
}void* producter(void* args)
{BlockQueue<int>* bqueue = (BlockQueue<int>*)args;int a = 1;while(true){  bqueue->push(a);cout << "生产了一个数据： " << a++ << endl;}return nullptr;
}int main()
{BlockQueue<int>* bqueue = new BlockQueue<int>();pthread_t c,p;pthread_create(&c,nullptr,consumer,bqueue);pthread_create(&p,nullptr,producter,bqueue);pthread_join(c,nullptr);pthread_join(p,nullptr);return 0;
}

然后我们运行这段程序，看看效果：

以上是单线程的，我们可以改成多线程的生产消费者模型，而且我们可以改成处理任务，而不是单纯的对一个变量进行修改，改成生产者进行产生加法式子，消费者计算结果并输出。

我们在主函数中，将内容改成如下：

int myAdd(int x , int y)
{sleep(1);return x + y;
}
void* consumer(void* args)
{BlockQueue<Task>* bqueue = (BlockQueue<Task>*)args;while(true){//获取任务Task t;bqueue->pop(&t);//完成任务cout << pthread_self() <<" consumer:" <<  t.x_ << "+" << t.y_ << " = "  << t() << endl;sleep(1);}return nullptr;
}void* producter(void* args)
{BlockQueue<Task>* bqueue = (BlockQueue<Task>*)args;//生产任务while(true){  //制作任务int x = rand() % 100 + 1;usleep(rand() % 1000);int y = rand() % 50 + 1;Task t(x,y,myAdd);//生产任务bqueue->push(t);//输出消息cout  << pthread_self() << " producter: " << t.x_ << "+" << t.y_ << "=?" << endl;sleep(1);}int main()
{srand((unsigned int) time(nullptr)^ getpid() ^ 1223);BlockQueue<Task>* bqueue = new BlockQueue<Task>();pthread_t c[2],p[2];for(int i = 0; i < 2; i++)pthread_create(c+i,nullptr,consumer,bqueue);for(int j = 0; j < 2; j++)pthread_create(p+j,nullptr,producter,bqueue);for(int i = 0; i < 2; i++)pthread_join(c[i],nullptr);for(int j = 0; j < 2; j++)pthread_join(p[j],nullptr);return 0;
}