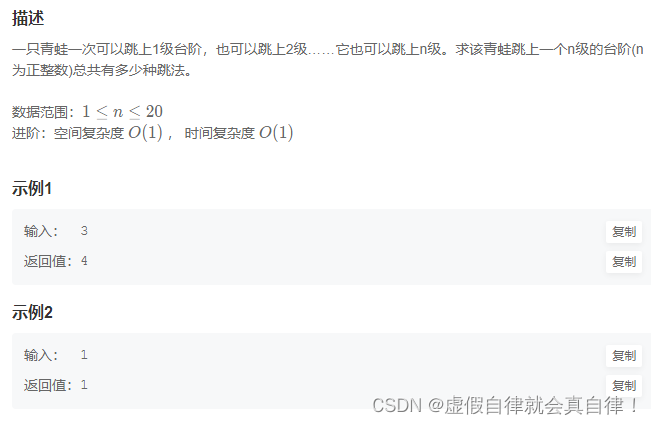
1. JZ83 剪绳子（进阶版）

class Solution {
public:int jumpFloorII(int number) {if(number <= 1) return number;int temp = 1;int res = 0;/*2级台阶 23级台阶 44级台阶 65级台阶 16*/for(int i=2; i<=number; i++){res = 2 * temp;temp = res;}return res;}
};

2. JZ70 矩形覆盖

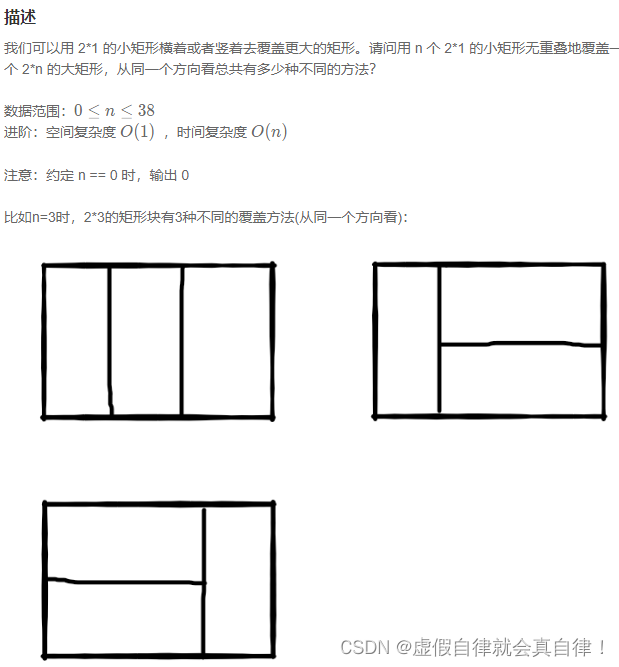
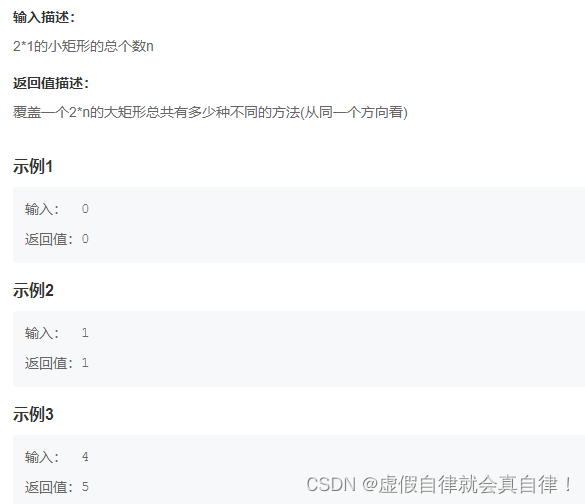
斐波那契鳄数列的另外一种形式，关注长就好，高永远是2

class Solution {
public:int rectCover(int number) {if(number <= 2) return number;int len1 = 1;int len2 = 2;int res = 0;for(int i=3; i<=number; i++){res = len1 + len2;len1 = len2;len2 = res;}return res;}
};

3. JZ63 买卖股票的最好时机(一)

class Solution {
public:int maxProfit(vector<int>& prices) {vector<vector<int>> dp(prices.size(), vector<int>(2,0));/*dp[i][]-第i天的收益 两种状态 0-不持股 1-持股dp[i][0]不持股收益，要么前一天就没有股票，今天也不买股票，收益不变；要么前一天有股票，今天卖出股票，收益加上卖出的钱dp[i][1]持股收益，要么前一天持有股票，今天不卖，收益不变；要么前一天没有股票，今天买入股票，收益减去买股票的钱*/dp[0][0] = 0;dp[0][1] = -prices[0];for(int i=1; i<prices.size(); i++){dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);dp[i][1] = max(dp[i-1][1], -prices[i]);}//最后一天不持股，到该天为止的最大收益return dp[prices.size()-1][0];}
};

4. JZ47 礼物的最大价值

class Solution {
public:int maxValue(vector<vector<int> >& grid) {int m = grid.size();        //行数int n = grid[0].size();     //列数vector<vector<int>> dp(m, vector<int>(n, 0));dp[0][0] = grid[0][0];//第一列只能来自上方for(int i=1; i<m; i++)dp[i][0] = dp[i-1][0] + grid[i][0];//第一行只能来自左边for(int j=1; j<n; j++)dp[0][j] = dp[0][j-1] + grid[0][j];for(int i=1; i<m; i++){for(int j=1; j<n; j++){dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + grid[i][j];}}return dp[m-1][n-1];}
};

使用原来的grid数组

5. JZ48 最长不含重复字符的子字符串

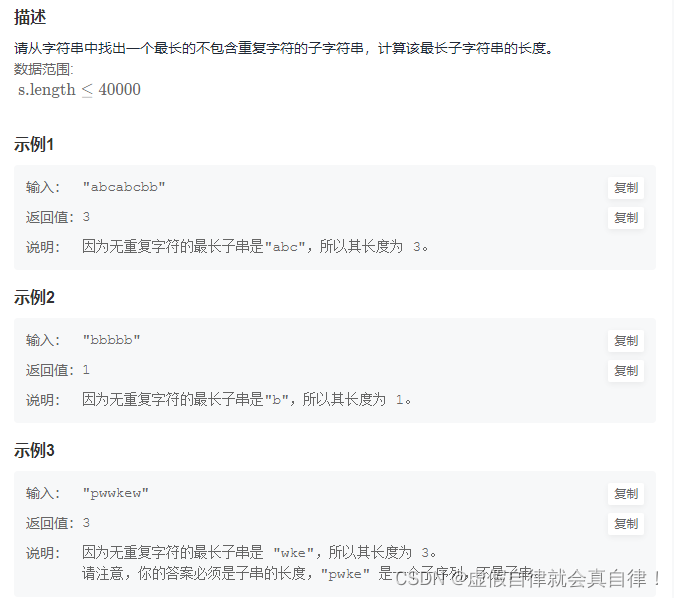
滑动窗口+哈希

class Solution {
public:int lengthOfLongestSubstring(string s) {//滑动窗口+哈希unordered_map<char, int> hashmap;int result = 0;for(int left=0, right=0; right<s.size(); right++){hashmap[s[right]]++;//统计频率//出现次数大于1，则窗口内有重复 while(hashmap[s[right]] > 1){hashmap[s[left]]--;//同时减去该字符的出现次数 把较早出现的字符移出窗口left++;//窗口左移}result = max(result, right - left + 1);}return result;}
};

动态规划

class Solution {
public:int lengthOfLongestSubstring(string s) {//动态规划if(s.size() <= 1) return s.size();int result = 0;vector<int> dp(s.size(), 0);dp[0] = 1;for(int j=1; j<s.size(); j++){int i = j - 1;//i就是距离j最近的相同字符位置while( j >= 0 && s[i] != s[j]) i--;//if(i<0) dp[j] = dp[j-1]+1;if(dp[j-1] < j-i) dp[j] = dp[j-1] + 1;//第i个字符不在dp[j-1]的区间之内else dp[j] = j-i;//第i个字符在dp[i-1]的区间之内if(dp[j] > result) result = dp[j];}return result;}
};

6. JZ46 把数字翻译成字符串

三种特殊情况剔除，0、10和20、0的前面不是1和2
动态规划，两种状态，1-9只有一种译码方案；10-19，21-26都有两种译码方案。

class Solution {
public:int solve(string nums) {//排除0if(nums == "0") return 0;//排除只有一种可能的10 和 20if(nums == "10" || nums == "20") return 1;//当0的前面不是1或2时，无法译码，0种for(int i = 1; i < nums.size(); i++){ if(nums[i] == '0')if(nums[i - 1] != '1' && nums[i - 1] != '2')return 0;}vector<int> dp(nums.size()+1, 1);for(int i=2; i<=nums.size(); i++){//在11-19，21-26之间的情况if((nums[i-2] == '1' && nums[i-1] != '0') || (nums[i-2] == '2' && nums[i-1] > '0' && nums[i-1] < '7'))dp[i] = dp[i-2] + dp[i-1];else dp[i] = dp[i-1];//在1-9 之间的情况}return dp[nums.size()];//size()是包括最后的\0 length()就是字符个数}
};

7. JZ21 调整数组顺序使奇数位于偶数前面(一)

插入排序思想，记录已经是奇数的位置下标（视作为有序区域），然后向后遍历，一经发现是奇数则进行“插入排序”，然后有序区下标加1。

class Solution {
public:vector<int> reOrderArray(vector<int>& array) {//记录已经是奇数的位置 要插入奇数的位置 i前面的数字都是排好序的int oddindex=0;        int temp = 0;for(int i=0; i<array.size(); i++){temp = array[i];//i 遇到奇数 先保存这个值，然后将 【i, j-1】数组后移动if((array[i] & 1) == 1){temp = array[i];for(int j=i-1; j>=oddindex; --j)array[j+1] = array[j];//再把 遇到的奇数插在 oddindex位置array[oddindex++] = temp;}}return array;}
};

8. JZ81 调整数组顺序使奇数位于偶数前面(二)

这个题和（一）的区别就是，数字的顺序可以不固定，所以就是两个指针遍历，奇数位是偶数与偶数位是奇数的两个数字交换就好啦。

class Solution {
public:vector<int> reOrderArrayTwo(vector<int>& array) {int left = 0;                   //偶数位 要求是奇数int right = array.size()-1;     //奇数位 要求是偶数while(left < right){while(left < right && (array[left] & 1) == 1) left++;//偶数位是奇数 跳过while(left < right && (array[right] & 1) == 0) right--;swap(array[left], array[right]);}return array;}
};

这种就是偶数放在前面，奇数放在后面

class Solution {
public:vector<int> reOrderArrayTwo(vector<int>& array) {int left = 0, right = array.size()-1;while(left < right){while(left < right && (array[left] & 1) != 1) left++;//偶数位是偶数while(left < right && (array[right] & 1) != 0) right--;swap(array[left], array[right]);}return array;}
};