【算法——双指针】LeetCode 11 盛最多水的容器

题目描述：

解题思路：

如图所示：

1、我们考虑相距最远的两个柱子所能容纳水的面积。宽度是两根柱子之间的距离8；高度取决于两根柱子之间较短的那个，即左边柱子的高度3。水的面积就是3×8=24。

2、如果选择固定一根柱子，另外一根变化，水的面积变化：

当前柱子是最两侧的柱子，水的宽度为最大，其它的组合，水的宽度都比这个小。
左边柱子较短，决定了水的高度为3。如果移动左边的柱子，新的水面高度不确定，一定不会超过右边的柱子高度7。
如果移动右边的柱子，新的水面高度一定不会超过左边的柱子高度3，也就是不会超过现在的水面高度。

3、因此，如果固定左边的柱子，移动右边的柱子，那么水的高度一定不会增加，且宽度一定减少，所以水的面积一定减少。这个时候，左边的柱子和任意一个其他柱子的组合，其实都可以排除了。也就是我们可以排除掉左边的柱子了。

4、这个排除掉左边柱子的操作，就是双指针代码里的left++。left和right两个指针中间的区域都是还未排除掉的区域。随着不断的排除，left和right都会往中间移动。当left和right相遇，算法就结束了。

代码：

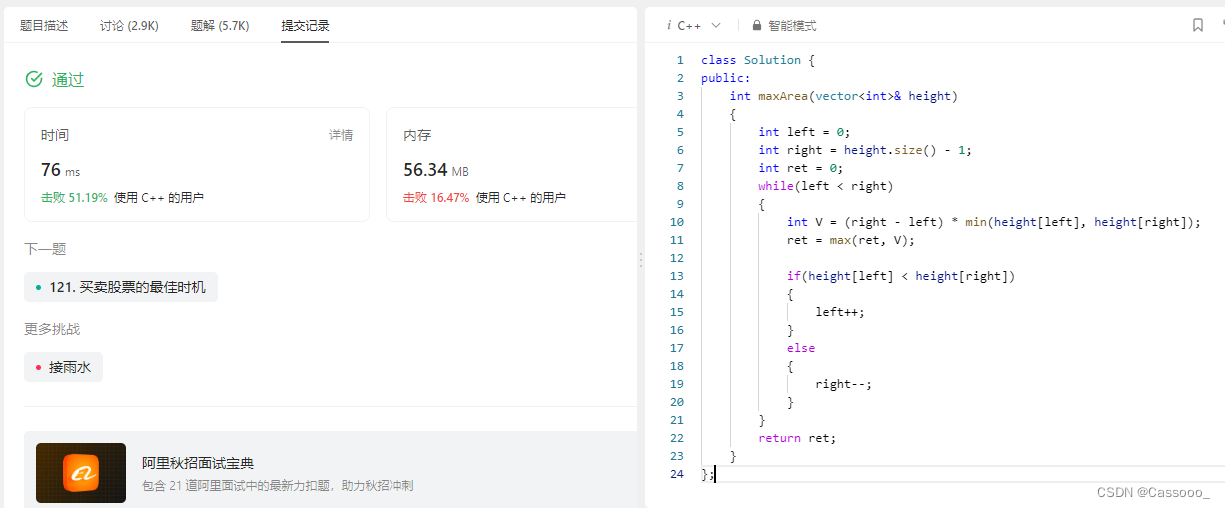
class Solution {
public:int maxArea(vector<int>& height) {int left = 0;int right = height.size() - 1;int ret = 0;while(left < right){int V = (right - left) * min(height[left], height[right]);ret = max(ret, V);if(height[left] < height[right]){left++;}else{right--;}}return ret;}
};