一、算法的稳定性

算法的稳定性指的是在排序过程中，相等元素的相对位置是否保持不变。如果算法是稳定的，那么相等元素在排序后的顺序与它们在原始序列中的顺序相同。稳定性在某些应用中非常重要，例如需要按多个条件排序时。

排序方法	平均情况	最好情况	最坏情况	辅助空间	稳定性
冒泡排序	O(n^2)	O(n)	O(n^2)	O(1)	稳定
简单选择排序	O(n^2)	O(n^2)	O(n^2)	O(1)	稳定
直接插入排序	O(n^2)	O(n)	O(n^2)	O(1)	稳定
希尔排序	O(n log n)~O(n^2)	O(n^1.3)	O(n^2)	O(1)	不稳定
堆排序	O(n log n)	O(n log n)	O(n log n)	O(1)	不稳定
归并排序	O(n log n)	O(n log n)	O(n log n)	O(n)	稳定
快速排序	O(n log n)	O(n log n)	O(n^2)	O(log n)~O(n)	不稳定

那么不稳定性又是什么呢？

具体来说，如果在原始序列中，元素 A 和元素 B 相等，且 A 在 B 之前，如果在排序后 A 仍然在 B 之前，那么排序算法就被称为是稳定的；如果排序后 A 和 B 的相对位置发生了改变，那么排序算法就是不稳定的。

为了更好地理解稳定性和不稳定性，让我们通过一个示例来说明，假设我们有一个待排序的数组，其中每个元素是一个包含姓名和年龄的记录，如下所示：

Name    Age
------------
Alice   25
Bob     30
Carol   25
David   22

现在我们要按照年龄进行排序，首先考虑使用快速排序，但快速排序是不稳定的排序算法。如果我们使用快速排序对年龄进行排序，可能会得到以下结果：

Name    Age
------------
David   22
Alice   25
Carol   25
Bob     30

在这个排序后的结果中，虽然 Alice 和 Carol 在原始序列中的相对位置是正确的，但是 Carol 和 David 的相对位置发生了改变，所以快速排序是不稳定的。

相比之下，如果我们使用稳定的排序算法，如冒泡排序或插入排序，对年龄进行排序，那么无论排序的结果如何，Alice 和 Carol 在排序后的序列中的相对位置仍然保持不变。

二、冒泡排序（Bubble Sort）

冒泡排序是一种简单的排序算法。它通过多次比较相邻元素的大小并交换位置，使得最大（或最小）的元素逐渐“冒泡”到数组的一端。冒泡排序的时间复杂度为O(n^2)，其中n是元素的数量。

代码实现：

#include <stdio.h>// 交换数组中的两个元素
void swap(int arr[], int i, int j)
{int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;
}// 冒泡排序
void bubbleSort(int arr[], int n)
{for(int i  = 0 ; i < n ; i ++){for (int j= 0 ; j < n - i -1; j++){if (arr[j] > arr[j+1]){swap(arr , j ,j+1);}}				}}//遍历
void display(int arr[], int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");}int main() {int arr[] = {64, 34, 25, 12, 22, 11, 90, 13, 14, 26, 27, 115, 91, 92, 84, 96, 86, 35, 37, 56, 58, 65, 10, 38, 99 , 105 , 88, 29};int n = sizeof(arr) / sizeof(arr[0]);printf("原始数组：\n");display(arr,n);//遍历bubbleSort(arr, n);printf("排序后的数组：\n");display(arr,n);//遍历return 0;
}

三、冒泡排序的改进：鸡尾酒排序

鸡尾酒排序是对冒泡排序的改进。它通过交替地进行正向和反向的冒泡扫描，从而在每一轮排序中同时处理数组的两端。这样可以更快地将较大和较小的元素分别移到正确的位置。

代码实现：

#include <stdio.h>
#include <time.h>// 交换数组中的两个元素
void swap(int arr[], int i, int j)
{int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;
}// 鸡尾酒排序
void cocktailSort(int arr[], int size)
{int left = 0;        // 数组的左边界int right = size - 1;// 数组的右边界while (left < right) // 当左边界小于右边界时继续排序{for (int i = left; i < right; i++) // 从左往右冒泡，将较大的元素往右边“冒”{if (arr[i] > arr[i + 1]){swap(arr, i, i + 1); // 如果相邻元素顺序错误，交换它们}}right--; // 右边界左移，排除已经排好序的元素for (int j = right; j > left; j--) // 从右往左冒泡，将较小的元素往左边“冒”{if (arr[j] < arr[j - 1]){swap(arr, j, j - 1); // 如果相邻元素顺序错误，交换它们}}left++; // 左边界右移，排除已经排好序的元素}
}//遍历
void display(int arr[], int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");}int main()
{int arr[] = {64, 34, 25, 12, 22, 11, 90, 13, 14, 26, 27, 115, 91, 92, 84, 96, 86, 35, 37, 56, 58, 65, 10, 38, 99, 105, 88, 29};int n = sizeof(arr) / sizeof(arr[0]);printf("原始数组：\n");display(arr, n);// 获取开始时间clock_t start_time = clock();cocktailSort(arr, n); // 调用鸡尾酒排序函数对数组排序// 获取结束时间clock_t end_time = clock();double total_time = (double)(end_time - start_time) / CLOCKS_PER_SEC;printf("排序后的数组：\n");display(arr, n);printf("运行时间：%f 秒\n", total_time);return 0;
}

四、选择排序（Selection Sort）

选择排序每次从未排序部分中选择最小（或最大）的元素，然后将其与未排序部分的起始位置交换。选择排序的时间复杂度为O(n^2)，其中n是元素的数量。虽然选择排序简单，但在大规模数据上效率较低。

代码实现：

#include <stdio.h>//交换数组中的两个元素
void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}//选择排序
void selectSort(int arr[], int size) {for (int i = 0; i < size - 1; i++) {int minIndex = i; // 假设当前位置为最小值的索引// 在未排序部分中查找最小值的索引for (int j = i+1; j < size; j++) {if (arr[j] < arr[minIndex]) {minIndex = j; // 更新最小值的索引}}// 如果最小值的索引不等于当前位置，进行交换if (minIndex != i) {swap(&arr[i], &arr[minIndex]); // 将最小值交换到当前位置}}
}

五、插入排序（Insertion Sort）

插入排序的核心思想是将未排序的元素逐个插入已排序的部分。它通过在已排序部分找到适当位置来插入元素，从而构建有序序列。插入排序的最好情况时间复杂度为O(n)，最坏情况为O(n^2)。

插入排序的理解可以结和玩扑克牌时顺序放牌。

代码实现：

// 插入排序
void insert_Sort(int arr[], int size) {for (int i = 1; i < size; i++) {int key = arr[i]; // 当前要插入的元素int j = i - 1;//拿到你当前元素的前一个元素的下标// 向前查找插入位置while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j]; // 将比 key 大的元素向后移动一个下标j--;//向前移动元素下标，可以理解为此时比key大的元素已经无需再比较，因此就把它的下标减去}//将key插入到正确位置，即key在当前元素之前arr[j + 1] = key;//为什么是加1，因为此时j值为 -1 加上1 为0，即最数组前方}
}

六、插入排序的更高效改进：希尔排序（Shell Sort）

希尔排序，也叫递减增量排序，是插入排序的一种更高效的改进版本。希尔排序是不稳定的排序算法。

　　希尔排序是基于插入排序的以下两点性质而提出改进方法的：

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

　　希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）。

　　假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n^2)的排序（冒泡排序或直接插入排序），可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据，所以小数据只需进行少数比较和交换即可到正确位置。

代码实现：

void ShellSort(int arr[], int n) {int h = 0;// 生成初始增量序列while (h <= n) {h = 3 * h + 1;}// 开始希尔排序while (h >= 1) {// 对每个增量间隔进行插入排序for (int i = h; i < n; i++) {int j = i - h;int get = arr[i];// 插入排序部分while (j >= 0 && arr[j] > get) {arr[j + h] = arr[j];j = j - h;}arr[j + h] = get; // 将当前元素插入正确的位置}h = (h - 1) / 3; // 递减增量序列}
}

七、快速排序（Quick Sort）

快速排序是一种高效的分治排序算法。它选择一个元素作为“基准”，将数组分成两部分，一部分小于基准，一部分大于基准。然后递归地对两部分进行排序。快速排序的平均时间复杂度为O(n log n)，但在最坏情况下可能达到O(n^2)。它通常比其他简单的排序算法更快，并且在实践中效果良好。

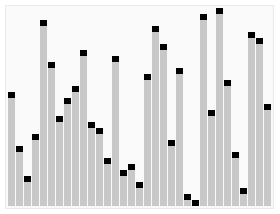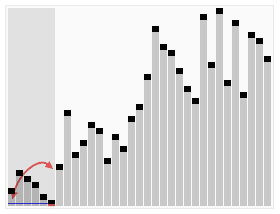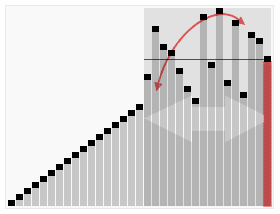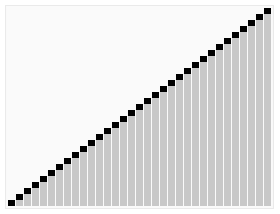
代码实现：

void QuickSort(int arr[], int left, int right) {// 边界条件：如果左边界大于等于右边界，直接返回if (left >= right) {return;}// 选取基准值int i = left, j = right;int pivot = arr[right]; // 以右边值作为基准while (i < j) {// 从左往右找第一个大于等于基准的元素while (i < j && arr[i] < pivot) {i++;}if (i < j) {arr[j] = arr[i]; // 将找到的大于等于基准的元素移到右边j--;}// 从右往左找第一个小于等于基准的元素while (i < j && arr[j] > pivot) {j--;}if (i < j) {arr[i] = arr[j]; // 将找到的小于等于基准的元素移到左边i++;}}arr[j] = pivot; // 基准值归位// 对基准值左边的子数组进行快速排序QuickSort(arr, left, i - 1);// 对基准值右边的子数组进行快速排序QuickSort(arr, i + 1, right);
}

更多C语言、Linux系统、ARM板实战和数据结构相关文章，关注专栏：

手撕C语言

玩转linux

脚踢数据结构

6818（ARM）开发板实战